

湖北省黄石市西塞山区六年级(下)期中数学试卷
展开
这是一份湖北省黄石市西塞山区六年级(下)期中数学试卷,共17页。试卷主要包含了填空题,判断题,选择题,计算题,动手操作,解决问题等内容,欢迎下载使用。
1. 1.02m3=________m3________dm3 4058mL=________L________mL.
2. 把地面20千米的距离用5厘米的线段画在地图上,那么,这幅地图的比例尺是________.
3. 在A×B=C中,当B一定时,A和C 成________比例,当C一定时,A和B成________比例。
4. 在一个比例中,两个比的比值都是3,这个比例的两个内项都是6,这个比例是________.
5. 男生人数比女生多15,男生人数是女生人数的( )( ),女生人数与男生人数的比是________:________,女生比男生少( )( ).
6. 大圆的半径与小圆半径的比是3:1,则大圆的面积是小圆的面积的________倍。
7. 24个实心铁圆锥,可以熔铸成与铁圆锥等底等高的实心圆柱________个。
8. 一个圆柱的底面直径是4cm,高是1dm,它的表面积是________cm2,体积是________cm3.
9. 一个长3cm、宽2cm的长方形按3:1放大,得到的图形的面积是________cm3.
10. 所有的负数都在0的________边,也就是负数都比0________,而正数都比0________.负数都比正数________.
二、判断题:(5分,每题1分)
11. 圆的面积和半径成正比例。________.(判断对错)
12. 两个圆柱形水池体积相等,容积也一定相等________.(判断对错)
13.把一个圆柱削成一个圆锥,这个圆锥的体积是圆柱体积的13.________.(判断对错)
14. 如果x=8y,那么x与y成正比例________.(判断对错)
15.成正比例的量,在图象上描的点连接起来是一条曲线________. (判断对错)
三、选择题:(5分,每题1分)
16. 如果AB=K+2(K一定),那么A和B成( )
A.正比例B.反比例C.无法确定D.不成比例
17. 把1.2吨:300千克化成最简整数比是( )
A.1:250B.1200:300C.4:1D.4
18.用一块长25.12厘米,宽18.84厘米的长方形铁皮,配上下面( )圆形铁片正好可以做成圆柱形容器。
A.无法计算B.d=3厘米
C.r=4厘米D.d=6厘米或8厘米
19.要反映食品中各种营养成份的含量,最好选用( )统计图。
A.复式统计表B.折线统计图C.扇形统计图D.条形统计图
20.一个圆柱的底面半径是1.5dm,侧面积是4dm2,这个圆柱的体积是( )
A.6dm3B.3dm3 dm3D.无法计算
四、计算题:(35分)
21. 直接写出得数:
解比例
计算(能简算的要简算).
1835÷60%×23 517÷9+19×1217 87×386 45÷[(13+25)×411].
五、动手操作:(5分)
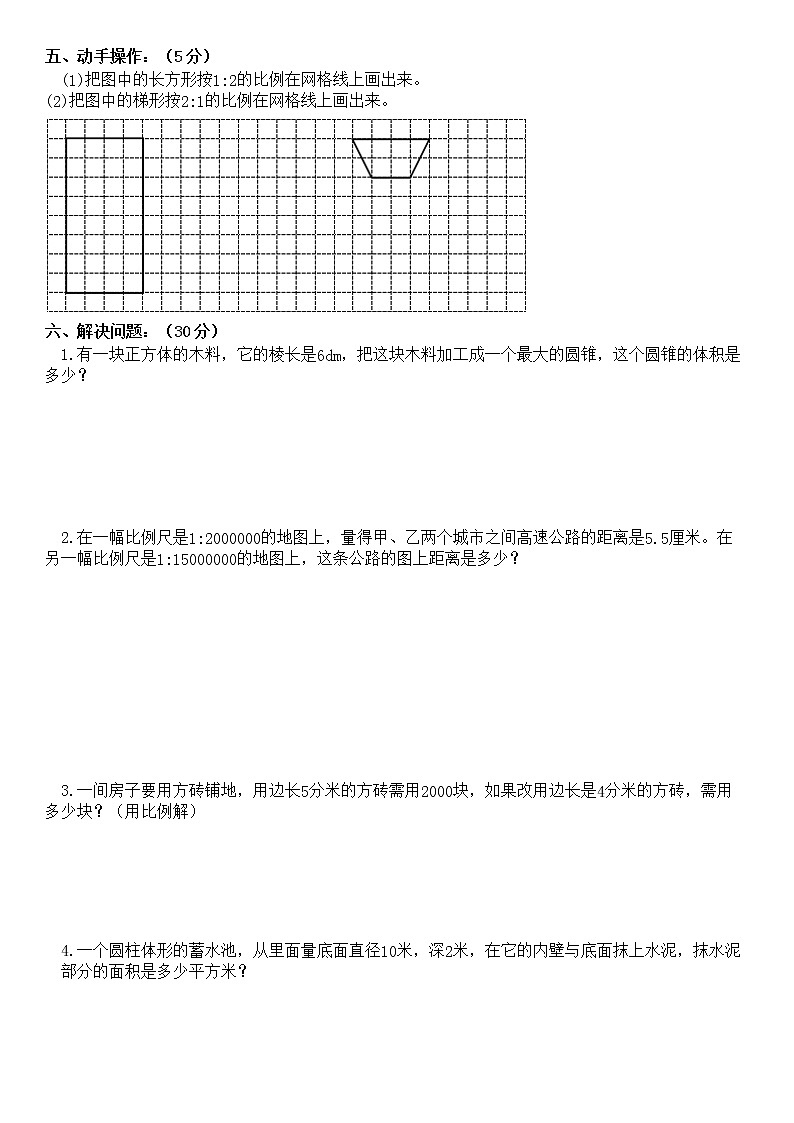
(1)把图中的长方形按1:2的比例在网格线上画出来。
(2)把图中的梯形按2:1的比例在网格线上画出来。
六、解决问题:(30分)
1.有一块正方体的木料,它的棱长是6dm,把这块木料加工成一个最大的圆锥,这个圆锥的体积是多少?
2.在一幅比例尺是1:2000000的地图上,量得甲、乙两个城市之间高速公路的距离是5.5厘米。在另一幅比例尺是1:15000000的地图上,这条公路的图上距离是多少?
3.一间房子要用方砖铺地,用边长5分米的方砖需用2000块,如果改用边长是4分米的方砖,需用多少块?(用比例解)
4.一个圆柱体形的蓄水池,从里面量底面直径10米,深2米,在它的内壁与底面抹上水泥,抹水泥部分的面积是多少平方米?
5. 一个圆锥形沙堆,高是2.5米,底面积是28.26平方米,用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?
6.“三八妇女节”时,小明送妈妈一只茶杯。
(1)这只茶杯占据桌面的大小是多少平方厘米?
(2)茶杯中部的一圈装饰带很漂亮,那是小明怕烫伤妈妈的手特意贴上的,这条装饰带宽5厘米,接头处1厘米,装饰带长多少厘米?
(3)这只茶杯能装多少毫升水?
参考答案与试题解析
2015-2016学年湖北省黄石市西塞山区六年级(下)期中数学试卷
一、填空题:(20分,每空1分)
1.
【答案】
1,20,4,58
【考点】
体积、容积进率及单位换算
【解析】
把1.02立方米换算为复名数,整数部分是立方米数,用0.02乘进率1000是立方分米数;
把4058毫升换算为复名数,用4058除以进率1000,商部分是升数,余数是毫升数。
【解答】
解:1.02m3=1m320dm3
4058mL=4L58mL
故答案为:1,20,4,58.
2.
【答案】
1:400000
【考点】
比例尺
【解析】
根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【解答】
解:20千米=2000000厘米,
5:2000000=1:400000;
答:这幅地图的比例尺是1:400000.
故答案为:1:400000.
3.
【答案】
正,反
【考点】
正比例和反比例的意义
【解析】
根据判断两种量成正比例还是成反比例的方法:关键是看这两种相关联的量中相对应的两个数的商一定还是积一定,如果商一定,就成正比例关系;如果积一定,就成反比例关系;进行解答即可。
【解答】
(1)因为A×B=C
所以C÷A=B(一定)
所以A和C成正比例。
(2)因为A×B=C(一定)
A和B成反比例。
故答案为:正,反。
4.
【答案】
18:6=6:2
【考点】
比例的意义和基本性质
【解析】
根据题意,可知求的是这个比例的两个外项,也就是第一个比缺比的前项,就用比值乘上比的后项;第二个比缺比的后项,就用比的前项除以比值;分别求出后,再写出比例即可。
【解答】
第一个比的前项:3×6=18,
第二个比的后项:6÷3=2,
这个比例式是:18:6=6:(2)
5.
【答案】
5,6
【考点】
比的意义
分数除法
【解析】
根据“男生比女生多15”,把女生人数看做5份数,男生人数就是5+1=6份数,用男生人数除以女生人数即可得解;用女生人数比上男生人数的份数、即可得解;先计算出他们的人数的份数之差,再除以男生人数,即可得解。
【解答】
解:(1)把女生人数看做5份数,男生人数就是5+1=6份数,
6÷5=65;
(2)女生人数:男生人数=5:6;
(3)(6−5)÷6=16;
故答案为:65、5:6、16.
6.
【答案】
9
【考点】
圆、圆环的面积
比的应用
【解析】
本题要根据圆的面积公式:S=πr2进行解答。
【解答】
大圆的半径与小圆半径的比是3:1则其面积比为:
S大:S小=π(3r2):πr2=9:1=9;
7.
【答案】
8
【考点】
圆锥的体积
圆柱的侧面积、表面积和体积
【解析】
本题是把圆锥熔铸成等底等高的圆柱体,由于一个圆柱的体积是与它等底等高的圆锥体积的3倍,也就是说,要3个这样的圆锥才能熔铸成1个等底等高的圆柱体,所以原题就是求24里面有几个3,据此解答。
【解答】
解:24÷3=8(个)
答:可以熔铸成与铁圆锥等底等高的实心圆柱8个。
故答案为:8.
8.
【答案】
150.72,125.6
【考点】
圆柱的侧面积、表面积和体积
【解析】
根据圆柱的表面积公式、体积公式,圆柱的表面积=侧面积+底面积×2,圆柱的体积=底面积×高,把数据分别代入公式解答即可。
【解答】
解:1分米=10厘米,
3.14×4×10+3.14×(4÷2)2×2
=125.6+3.14×4×2
=125.6+12.56×2
=125.6+25.12
=150.72(平方厘米);
3.14×(4÷2)2×10
=3.14×4×10
=12.56×10
=125.6(立方厘米);
答:这个圆柱的表面积是150.72平方厘米,体积是125.6立方厘米。
故答案为:150.72;125.6.
9.
【答案】
54
【考点】
图形的放大与缩小
【解析】
此题只要求出放大后的长和宽,根据“图上距离=实际距离×比例尺”可求出;然后根据“长方形的面积=长×宽”即可得出结论。
【解答】
解:3×3=9(厘米)
3×2=6(厘米)
9×6=54(平方厘米)
答:得到的图形的面积是54平方厘米。
故答案为:54.
10.
【答案】
左,小,大,小
【考点】
正、负数大小的比较
【解析】
此题考查了数轴的认识,数轴上的点和数一一对应,原点记作0,负数在原点左边,正数在原点右边,从左向右数字越来越大。由此得解。
【解答】
解:所有的负数都在0的左边,也就是负数都比0小,而正数都比0大。负数都比正数小。
故答案为:左,小,大,小。
二、判断题:(5分,每题1分)
【答案】
错误
【考点】
辨识成正比例的量与成反比例的量
【解析】
判断圆的面积和半径是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例。
【解答】
解:因为圆的面积S=πr2,
所以S:r2=π(一定),
即圆的面积与半径的平方的比值一定,但圆的面积与半径的比值不是一定的,
不符合正比例的意义,所以圆的面积和半径不成正比例;
故答案为:错误。
【答案】
×
【考点】
圆柱的侧面积、表面积和体积
【解析】
根据体积、容器的意义,物体所占空间的大小叫做物体的体积。某容器所能容纳别的物体的体积叫做这个容器的容积。两个水池的体积相等,因为水池壁的厚度不一定相等,所以两个水池的容积就不一定相等。据此判断。
【解答】
解:两个水池的体积相等,因为水池壁的厚度不一定相等,所以两个水池的容积就不一定相等。
因此,两个圆柱形水池体积相等,容积也一定相等。这种说法是错误的。
故答案为:×.
【答案】
×
【考点】
圆锥的体积
【解析】
只有等底等高的圆锥的体积是圆柱体积的13,据此判断。
【解答】
把一个圆柱削成一个与它等底等高的圆锥,这个圆锥的体积是圆柱体积的13,如果没有确定削成的圆锥是否与圆柱等底等高,那么把一个圆柱削成一个圆锥,这个圆锥的体积是圆柱体积的13,这种说法是错误的。
【答案】
√
【考点】
辨识成正比例的量与成反比例的量
【解析】
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】
解:如果x=8y,即x:y=8,是比值一定,那么x与y成正比例;
故答案为:√.
【答案】
×
【考点】
正、反比例
【解析】
成正比例的两种量是对应的比值一定,也就是说一种量变化,另一种量也随着变化,它们的变化方向相同,所以成正比例的量,在图象上描的点连接起来是一条直线。
【解答】
成正比例的量,在图象上描的点连接起来是一条经过原点的直线,本题说法错误。
三、选择题:(5分,每题1分)
【答案】
B
【考点】
辨识成正比例的量与成反比例的量
【解析】
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】
解:如果AB=K+2(K一定),K一定,则K+2也是一定的,是乘积一定,那么A和B成反比例;
故选:B.
【答案】
C
【考点】
求比值和化简比
【解析】
因为“吨”和“千克”单位名数不同,要先统一单位再化简比。
【解答】
1.2吨:300千克,
=1200千克:300千克,
=4:1.
【答案】
D
【考点】
圆柱的侧面积、表面积和体积
【解析】
根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长、宽等于圆柱的高,根据圆的周长公式:c=πd,那么d=c÷π,据此求出直径,问题即可得到解决。
【解答】
25.12÷3.14=8(厘米),
18.84÷3.14=6(厘米),
答:可以配上直径6厘米或8厘米的圆形铁片正好做成圆柱形容器。
故选:D.
【答案】
C
【考点】
统计图的选择
【解析】
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解答】
解:根据统计图的特点可知:要反映食品中各种营养成份的含量,最好选用扇形统计图;
故选:C.
【答案】
B
【考点】
圆柱的侧面积、表面积和体积
【解析】
首先用圆柱的侧面积除以底面周长求出高,再根据圆柱的体积公式:v=sℎ,把数据代入公式解答。
【解答】
解:3.14×1.52×[4÷(3.14×1.5×2)]
=3.14×2.25×[4÷9.42]
≈7.065×0.42
=2.9673(立方分米)
≈3(立方分米),
答:这个圆柱的体积约是3立方分米。
故选:B.
四、计算题:(35分)
【答案】
【考点】
百分数的加减乘除运算
分数除法
【解析】
本题根据小数,分数的加法、乘法与除法的运算法则计算即可。
【解答】
【答案】
解:13x=2×35,
13x=65,
解得x=335;
4.6x=5×0.46,
4.5x=2.3,
解得x=0.5;
111x=18×222,
x=18×222111,
解得x=36;
4x=5×1.2,
4x=6,
解得x=1.5;
0.25x=1.25×1.6,
0.25x=2,
解得x=8;
3x=12×34,
3x=9,
解得x=3.
【考点】
解比例
【解析】
根据两内项之积等于两外项之积把比例式转化为乘积式,然后再解关于x的一元一次方程即可。
【解答】
解:13x=2×35,
13x=65,
解得x=335;
4.6x=5×0.46,
4.5x=2.3,
解得x=0.5;
111x=18×222,
x=18×222111,
解得x=36;
4x=5×1.2,
4x=6,
解得x=1.5;
0.25x=1.25×1.6,
0.25x=2,
解得x=8;
3x=12×34,
3x=9,
解得x=3.
【答案】
解:(1)1835÷60%×23
=67×23
=47;
(2)517÷9+19×1217
=517×19+19×1217
=(517+1217)×19
=1×19
=19;
(3)87×386
=(86+1)×386
=86×386+1×386
=3+386
=3386;
(4)45÷[(13+25)×411]
=45÷[1115×411]
=45÷415
=3.
【考点】
分数的四则混合运算
分数的简便计算
【解析】
(1)按照从左向右的顺序进行计算;
(2)、(3)根据乘法分配律进行简算;
(4)先算小括号里面的加法,再算中括号里面的乘法,最后算除法。
【解答】
解:(1)1835÷60%×23
=67×23
=47;
(2)517÷9+19×1217
=517×19+19×1217
=(517+1217)×19
=1×19
=19;
(3)87×386
=(86+1)×386
=86×386+1×386
=3+386
=3386;
(4)45÷[(13+25)×411]
=45÷[1115×411]
=45÷415
=3.
五、动手操作:(5分)
【答案】
解:根据分析画图如下:
【考点】
图形的放大与缩小
【解析】
(1)把图中的长方形按1:2的比例在网格线上画出来,就是把原来的长方形的长和宽都缩小到原来的12.原长方形长8格,宽4格,缩小后的长方形长是4格,宽是2格;
(2)把图中的梯形按2:1的比例在网格线上画出来,就是把原梯形的上底、下底、高都扩大到原来的2倍。原梯形上底、下底和高分别是2格、4格和2格,放大后的梯形的 上底、下底和高分别是4格,8格和4格。
【解答】
解:根据分析画图如下:
六、解决问题:(30分)
【答案】
这个圆锥的体积是56.52立方分米
【考点】
圆锥的体积
【解析】
根据题意可知:把棱长是6分米的正方体木料加工成一个最大的圆锥,这个圆锥的底面直径和高都等于正方体的棱长,根据圆锥的体积公式:v=13sℎ,把数据代入公式解答。
【解答】
13×3.14×(6÷2)2×6
=13×3.14×9×6
=56.52(立方分米),
【答案】
解:根据分析可得,
12000000÷115000000=7.5倍,
5.5÷7.5=1115(厘米);
答:这条公路的图上距离是1115厘米。
【考点】
图上距离与实际距离的换算(比例尺的应用)
【解析】
先求出第一幅比例尺是另一幅比例尺的几倍,列式为:12000000÷115000000=7.5倍,那么甲、乙两个城市之间高速公路的距离是5.5厘米就相当于另一幅图上距离的7.5倍,据此解答。
【解答】
解:根据分析可得,
12000000÷115000000=7.5倍,
5.5÷7.5=1115(厘米);
答:这条公路的图上距离是1115厘米。
【答案】
设需用x块,
4×4×x=5×5×2000
16x=25×2000
16x÷16=50000÷16
x=3125
答:需用3125块
【考点】
正、反比例应用题
【解析】
根据一间房子的地板面积一定,方砖的块数与方砖的面积成反比例,由此列出比例解决问题。
【解答】
设需用x块,
4×4×x=5×5×2000
16x=25×2000
16x÷16=50000÷16
x=3125
答:需用3125块
【答案】
解:3.14×10×2+3.14×(10÷2)2
=62.8+3.14×25
=62.8+78.5
=141.3(平方米)
答:抹水泥部分的面积是141.3平方米。
【考点】
关于圆柱的应用题
【解析】
抹水泥部分的面积就是这个圆柱形水池一个底面积和侧面积的和,再利用侧面积=底面周长×高和圆的面积公式S=πr2=π(d÷2)2,即可解答。
【解答】
解:3.14×10×2+3.14×(10÷2)2
=62.8+3.14×25
=62.8+78.5
=141.3(平方米)
答:抹水泥部分的面积是141.3平方米。
【答案】
2厘米=0.02米,
13×28.26×2.5÷(10×0.02)
=9.42×2.5÷0.2
=23.55÷0.2
=117.75(米)
答:能铺117.75米
【考点】
长方体和正方体的体积
圆锥的体积
【解析】
要求能铺多少米,首先根据圆锥的体积公式:v=13sℎ,求出沙堆的体积,把这堆沙铺在长方形的路面上就相当于一个长方体,只是形状改变了,但沙的体积没有变,因此,用沙的体积除以长方体的长再除以高就是所铺的长度。由此列式解答。
【解答】
2厘米=0.02米,
13×28.26×2.5÷(10×0.02)
=9.42×2.5÷0.2
=23.55÷0.2
=117.75(米)
答:能铺117.75米
【答案】
解:(1)3.14×(6÷2)2
=3.14×9
=28.26(平方厘米)
答:这只茶杯占据桌面的大小是28.26平方厘米。
(2)3.14×6=18.84(厘米)
答:长至少有18.84厘米。
(3)28.26×15=423.9(立方厘米)
423.9立方厘米=423.9毫升
答:这只茶杯能装423.9毫升水
【考点】
关于圆柱的应用题
【解析】
(1)这只茶杯占据桌面的面积等于圆柱的底面积,根据圆的面积公式S=πr2=π(d÷2)2解答。
(2)这条装饰带的长是直径为6厘米的圆的周长与接头外长度的和,根据圆的周长公式:C=πd可求出圆的周长;
(3)根据圆柱的容积公式:v=sℎ,把数据代入公式解答。
【解答】
解:(1)3.14×(6÷2)2
=3.14×9
=28.26(平方厘米)
答:这只茶杯占据桌面的大小是28.26平方厘米。
(2)3.14×6=18.84(厘米)
答:长至少有18.84厘米。
(3)28.26×15=423.9(立方厘米)
423.9立方厘米=423.9毫升
答:这只茶杯能装423.9毫升水1.2÷12%=
9−1.9=
7.2÷6=
0.24×34=
45÷23=
3.14×22=
14−15=
1+30%=
12+57=
0.52=
35:X=13:2
X:5=0.46:4.6
18111=X222
1.2x=45
1.25:0.25=x:1.6
34:x=3:12
解:1.2÷12%=10
9−1.9=7.1
7.2÷6=1.2
0.24×34=0.18
45÷23=65
3.14×22=69.08
14−15=120
1+30%=1.3
12+57=1714
0.52=0.25
解:1.2÷12%=10
9−1.9=7.1
7.2÷6=1.2
0.24×34=0.18
45÷23=65
3.14×22=69.08
14−15=120
1+30%=1.3
12+57=1714
0.52=0.25
相关试卷
这是一份2023-2024学年湖北省黄石市西塞山区三年级(上)核心素养数学试卷,共13页。试卷主要包含了填空,选择正确的答案.将序号填在,按要求计算下面各题,操作题,解决实际问题,附加题等内容,欢迎下载使用。
这是一份2023年湖北省黄石市西塞山区小升初数学试卷(内含答案解析),共14页。试卷主要包含了填空,判断题,选择题,计算题,操作题,解决问题等内容,欢迎下载使用。
这是一份2022-2023学年湖北省黄石市西塞山区五年级(下)期末数学试卷,共18页。试卷主要包含了填空题,判断题,选择题,计算题,操作题,解决问题等内容,欢迎下载使用。









