专题08 立体几何初步（基础巩固）-2021年暑假高一升高二数学复习基础巩固+能力提升专题（人教A版2019）

【新教材2019人教必修第二册】

暑假高一基础巩固 专题08  立体几何初步模块

解析版

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．（2021·江苏高一课时练习）下列命题中正确的是（    ）

A．正方形的直观图是正方形

B．平行四边形的直观图是平行四边形

C．有两个面平行，其余各面都是平行四边形的几何体叫棱柱

D．用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台

【答案】B

【分析】

选项，正方形的直观图是平行四边形；选项，由斜二测画法规则知平行性不变知②正确；选项，要注意棱柱的每相邻两个四边形的公共边互相平行；选项，用一个平行于底面的平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台．

【详解】

解：选项，正方形的直观图是平行四边形，故错误；

选项，由斜二测画法规则知平行性不变，即平行四边形的直观图是平行四边形，故②正确；

选项，有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱，要注意棱柱的每相邻两个四边形的公共边互相平行，故错误；

选项，用一个平行于底面的平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台，故错误．

故选：．

2．（2021·江西景德镇市·景德镇一中高一期末（理））若水平放置的四边形按“斜二测画法”得到如图所示的直观图，其中，，，，则原四边形的面积为（    ）

A．12 B．6 C． D．

【答案】C

【分析】

根据图像，由“斜二测画法”可得，四边形水平放置的直观图为直角梯形，进而利用相关的面积公式求解即可

【详解】

根据图像可得，四边形水平放置的直观图为直角梯形，

作，则，

由，得，，

，，且，，所以，

原四边形的面积为.

故选：C

3．（2020·浙江杭州市·高一期末）用一个平面去截正方体，则截面不可能是

A．直角三角形 B．等边三角形 C．正方形 D．正六边形

【答案】A

【详解】

画出截面图形如图

显然A正三角形C正方形：

D正六边形

可以画出三角形但不是直角三角形；

故选A．

用一个平面去截正方体，则截面的情况为：

①截面为三角形时，可以是锐角三角形、等腰三角形、等边三角形，但不可能是钝角三角形、直角三角形；

②截面为四边形时，可以是梯形（等腰梯形）、平行四边形、菱形、矩形，但不可能是直角梯形；

③截面为五边形时，不可能是正五边形；

④截面为六边形时，可以是正六边形．

故可选A．

4．（2020·江北区·重庆十八中高二期中）攒尖是古代中国建筑中屋顶的一种结构形式．宋代称为撮尖，清代称攒尖．依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等，也有单檐和重檐之分，多见于亭阁式建筑．如图所示，某园林建筑为六角攒尖，它的主要部分的轮廓可近似看作一个正六棱锥，若此正六棱锥的侧面等腰三角形的底角为，则侧棱与底面外接圆半径的比为（    ）

A． B． C． D．

【答案】A

【分析】

根据正六棱锥的底面为正六边形计算可得结果.

【详解】

正六棱锥的底面为正六边形，设其外接圆半径为，则底面正边形的边长为，

因为正六棱锥的侧面等腰三角形的底角为，

所以侧棱长为，

所以侧棱与底面外接圆半径的比为.

故选：A

【点睛】

关键点点睛：掌握正六棱锥的结构特征是解题关键.

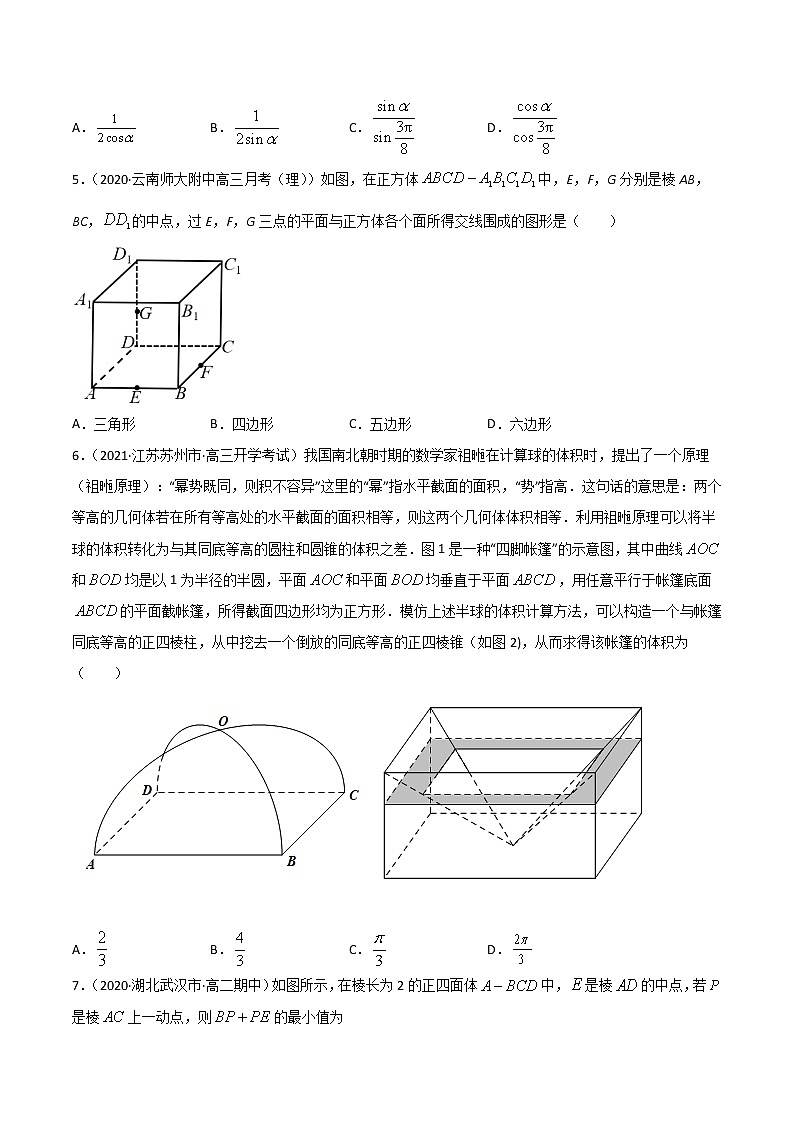
5．（2020·云南师大附中高三月考（理））如图，在正方体中，E，F，G分别是棱AB，BC，的中点，过E，F，G三点的平面与正方体各个面所得交线围成的图形是（    ）

A．三角形 B．四边形 C．五边形 D．六边形

【答案】C

【分析】

利用平面的性质，直接画出过E，F，G的平面，即可判断其形状.

【详解】

如图示，过E，F，G的平面α交AA1于H，交CC1于I,则形成一个五边形EFIGH.

故选：C.

6．（2021·江苏苏州市·高三开学考试）我国南北朝时期的数学家祖暅在计算球的体积时，提出了一个原理（祖暅原理）：“幂势既同，则积不容异”这里的“幂”指水平截面的面积，“势”指高．这句话的意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体体积相等．利用祖暅原理可以将半球的体积转化为与其同底等高的圆柱和圆锥的体积之差．图1是一种“四脚帐篷”的示意图，其中曲线和均是以1为半径的半圆，平面和平面均垂直于平面，用任意平行于帐篷底面的平面截帐篷，所得截面四边形均为正方形．模仿上述半球的体积计算方法，可以构造一个与帐篷同底等高的正四棱柱，从中挖去一个倒放的同底等高的正四棱锥（如图2)，从而求得该帐篷的体积为（    ）

A． B． C． D．

【答案】B

【分析】

根据题意，求得对应正四棱柱的底面边长和高，根据帐篷的体积等于棱柱的体积减去棱锥的体积，根据体积公式求得结果.

【详解】

根据题意，底面正方形的边长为，高为1，

根据题意，可知该帐篷的体积为，

故选：B.

【点睛】

方法点睛：该题考查的是有关几何体体积的求解，解题方法如下：

（1）认真读题，理解题意；

（2）根据题意，求得相应几何体的棱长；

（3）利用体积公式求得结果.

7．（2020·湖北武汉市·高二期中）如图所示，在棱长为2的正四面体中，是棱的中点，若是棱上一动点，则的最小值为

A． B． C． D．

【答案】B

【详解】

试题分析：将翻折到同一平面内，的最小值为为的长，在中，由余弦定理可得

考点：1．翻折问题；2．空间距离

8．（2020·山东德州市·高一期末）《九章算术》是我国古代数学名著﹐它在几何学中的研究比西方早多年.在《九章算术》中，将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图是阳马，平面，.则该阳马的外接球的表面积为（    ）

A． B． C． D．

【答案】B

【分析】

连接AC，BD，交于，取PC中点O，连接，则可证明平面ABCD，即O为该四棱锥的外接球的球心，在中，求得PC的值，进而可求得外接球半径R，代入公式，即可求得答案.

【详解】

连接AC，BD，交于，取PC中点O，连接，如图所示

因为分别为PC，AC的中点，

所以，

又平面ABCD，

所以平面ABCD，

所以O到A,B,C,D的距离都相等，又，

所以O为该四棱锥的外接球的球心，

在中，，，

所以，

所以该四棱锥的外接球的半径，

所以该阳马的外接球的表面积.

故选：B

二、多选题

9．（2020·江苏高一期中）设，是两条不同的直线，，是两个不同的平面，下列命题是假命题的是（    ）

A．若，，则 B．若，，则

C．若，，则 D．若，，则

【答案】ABC

【分析】

根据空间直线与平面、平面与平面的位置关系逐个分析可得答案.

【详解】

若，，则或与相交，故为假命题；

若，，则或与相交或与异面，故为假命题；

若，，则或或或与相交且不垂直，故为假命题；

若，，则，根据面面垂直的判定定理可知其为真命题.

故选：A B C

【点睛】

关键点点睛：掌握空间直线与平面、平面与平面的位置关系是解题关键.

10．（2021·江苏高一课时练习）(多选题)如图，正方体中，若分别为棱的中点，分别是四边形，的中心，则（ ）

A．四点共面

B．四点共面

C．四点共面

D．四点共面

【答案】ACD

【分析】

对于A，易知共面，再判断是否在这个平面即可；对于B，显然在平面内，D不在平面内，可知四点不共面；对于C，由已知可知，可判断四点共面；对于D，连接并延长，交于H，连接，可知，可判断四点共面.

【详解】

对于A，由是四边形的中心，知是的中点，所以在平面内，所以四点共面，故A正确；

对于B，由分别为棱的中点，知在平面内，D不在平面内，所以四点不共面，故B错误；

对于C，由已知可知，所以四点共面，故C正确；

对于D，连接并延长，交于H，则H为的中点，连接，则，所以四点共面，故D正确；

故选：ACD

【点睛】

方法点睛：本题考查点共面问题的证明，证明点或线共面问题的两种方法：①首先由所给条件中的部分线(或点)确定一个平面，然后再证其余的线(或点)在这个平面内；②将所有条件分为两部分，然后分别确定平面，再证两平面重合．

11．（2020·湖北高三月考）我国古代《九章算术》中将上、下两个面为平行矩形的六面体成为刍童.如图刍童有外接球，且，平面与平面的距离为1，则下列说法中正确的有（    ）

A．该刍童外接球的体积为 B．该刍童为棱台

C．该刍童中在一个平面内 D．该刍童中二面角的余弦值为

【答案】AD

【分析】

作出图形，设球心为O，上下底面的中心为，A.在中，，在中，，两式求得半径即可判断；B.根据棱台的几何特征判断；C.根据根据棱台的几何特征判断；D.过点F作平面ABCD，，连接MN，由为二面角的平面角求解判断.

【详解】

如图所示：

设球心为O，上下底面的中心为，

在中，，即，

在中，，即，

两式解得，

所以，则，故A正确；

若该刍童为棱台，则满足,而，故B错误；

若该刍童中在一个平面内，则，则,而，故C错误；

过点F作平面ABCD，，连接MN，则为二面角的平面角，

易知FM=1，，所以 ，故D正确；

故选：AD

12．（2021·广东梅州市·高三一模）如图，在正方体中，点在线段上运动时，下列命题正确的是（    ）

A．三棱锥的体积不变 B．直线与平面所成角的大小不变

C．直线与直线所成角的大小不变 D．二面角的大小不变

【答案】ACD

【分析】

根据线面位置关系分别判断各选项对错.

【详解】

A：平面，上任意一点到平面的距离相等，所以体积不变，A选项正确；

B：与平面相交，所以直线与平面所成角的大小在变，B选项错误；

C：直线平面，，直线与直线所成角的大小不变；C选项正确；

D：二面角也就是二面角大小不变，D选项正确；

故选：ACD.

三、填空题

13．（2021·浙江高三月考）用一个平行于圆锥底面的平面截该圆锥，截得圆台的上、下底面半径之比是1 : 4，截取的小圆锥的母线长是cm，则圆台的母线长______cm．

【答案】9.

【解析】

试题分析：设圆台的母线长为,截得圆台的上、下底面半径分别为.

根据相似三角形的性质得,解得.所以,圆台的母线长为9cm.

考点：空间几何体的结构.

14．（2020·重庆市万州第二高级中学高二月考）如图所示，平面平面，，，，则__________．

【答案】3

【分析】

利用平面平面，得到，从而得到线段长的比例，即可得解.

【详解】

平面，平面

由平面平面，可得

由平面几何知识知，

又，，，

所以，解得

故答案为：3

【点睛】

本题考查了面面平行的性质定理，在运用面面平行的性质定理时，一定要先找到与两平行平面都相交的第三个平面，进而得到两交线平行，考查学生的逻辑推理与运算能力，属于基础题.

15．（2020·山东省济南第十一中学高二期中）在四面体中，，，两两垂直.设，则点到平面的距离为______.

【答案】

【分析】

利用等积法可求点到平面的距离.

【详解】

因为，，两两垂直，而，故平面，

又，故.

又中，，故，同理，

故为等边三角形，故，

故，其中为点到平面的距离，

因为，故，故.

故答案为：.

【点睛】

方法点睛：（1）求点到平面的距离，利用线面垂直来考虑；（2）如果线面垂直构造比较困难，则可以考虑利用等积法来求点到平面的距离.

16．（2020·梅河口市第五中学高三月考（文））瑞士数学家、物理学家欧拉发现任一凸多面体（即多面体内任意两点的连线都被完全包含在该多面体中，直观上讲是指没有凹陷或孔洞的多面体）的顶点数、棱数及面数满足等式，这个等式称为欧拉多面体公式，被认为是数学领域最漂亮、简洁的公式之一，现实生活中存在很多奇妙的几何体，现代足球的外观即取自一种不完全正多面体，共有32个面，是由块白色正六边形面料和块黑色正五边形面料构成的.则的值为______.

【答案】20

【分析】

求出顶点数和棱数，然后代入欧拉多面体公式可得值．

【详解】

由题意该几何体的顶点为，棱数为，又，

由欧拉多面体公式得，解得．

故答案为：20．

【点睛】

本题考查数学文化，考查欧拉多面体公式的应用，解题关键是根据题意求出顶点数和棱数．

四、解答题

17．（2021·浙江丽水市·高二月考）如图，在四棱锥中，是正方形，平面，为线段中点，， 分别是的中点.

（1）求证：平面平面；

（2）求证：平面.

【答案】（1）证明见解析；（2）证明见解析.

【分析】

（1）证明平面和平面，即得证；

（2）连接，证明和，平面即得证.

【详解】

（1）分别是线段的中点，

所以，又为正方形，，

所以，

又平面，所以平面.

因为分别是线段的中点，所以，

又平面，所以平面.

因为平面，

所以平面平面.

（2）连接，

由于，所以为平面四边形，

由平面，得，

又，，所以平面，

所以，

又三角形为等腰直角三角形，为斜边中点，所以，

因为，平面.，

所以平面.

【点睛】

方法点睛：证明空间直线和平面的位置关系常用的方法：（1）转化法：线线线面面面；（2）向量法. 解题时要根据已知条件灵活选择方法求解.

18．（2021·浙江高一期末）如图，正方体中，F为与的交点，E为的中点．

（1）求证：平面；

（2）求异面直线与所成的角．

【答案】（1）证明见解析；（2）

【分析】

（1）联结EF，易知，从而证得平面；

（2）分别证得，，从而平面，从而异面直线与所成的角为90°.

【详解】

（1）联结EF，

由E为的中点，F为的中点知，，

又平面，平面，

故平面

（2）在正方形ABCD中，，又平面ABCD，平面ABCD，

则，又，

故平面，又平面，

故，即异面直线与所成的角为

【点睛】

方法点睛：通过在平面上找到一条直线与平面外一条线平行，来证明线面平行；异面直线的夹角可以通过平移到同一平面内，用解三角形的办法求得.

19．（2020·湖北高二月考）有一堆规格相同的铁制（铁的密度是）六角螺母共重5.8kg.如图，每一个螺母的底面是正六边形，边长为12mm，内孔直径为10mm，高为10mm，这堆螺母大约有多少个？（可用计算工具，π取3.14）

【答案】248个

【分析】

首先计算一个螺母的体积，其体积是六棱柱体积与圆柱体积的差，再由总重量除以一个螺母的重量，即可得解.

【详解】

解：六角螺帽的体积是六棱柱体积与圆柱体积的差，即：

.

所以螺帽的个数为（个）.

答：这堆螺帽大约有248个.

【点睛】

本题考查组合体的体积计算，属于基础题.

20．（2020·横峰中学高二月考）如图，四棱锥的底面是边长为2的菱形，底面.

（1）求证：平面；

（2）若，直线与平面所成的角为，求四棱锥的体积.

【答案】（1）证明见解析；（2）

【分析】

（1）通过AC⊥BD与PD⊥AC可得平面；

（2）由题先得出∠PBD是直线PB与平面ABCD所成的角，即∠PBD=45°，则可先求出菱形ABCD的面积，进而可得四棱锥P- ABCD的体积.

【详解】

解：（1）因为四边形ABCD是菱形，所以AC⊥BD，

又因为PD⊥平面ABCD，平面ABCD，

所以PD⊥AC，又，

故AC⊥平面PBD；

（2）因为PD⊥平面ABCD，

所以∠PBD是直线PB与平面ABCD所成的角，

于是∠PBD=45°，

因此BD=PD=2.又AB= AD=2，

所以菱形ABCD的面积为，

故四棱锥P- ABCD的体积.

【点睛】

本题主要考查空间线、面关系等基础知识，同时考查空间想象能力、推理论证能力以及运算求解能力，是基础题.

21．（2020·上海市七宝中学高二期末）已知正方体中的棱长为，是中点.

（1）求证：平面；

（2）设的中点为，过、、作一截面，求出截面面积．

【答案】（1）证明见解析；（2）.

【分析】

（1）连接、交于点，连接，证明出四边形为平行四边形，可得出，利用线面平行的判定定理可得出结论；

（2）作出截面图形，判断出截面图形的形状，并求出各边边长，由此可求得截面面积.

【详解】

（1）记、的交点为，则为的中点，

在正方体中，且，则四边形为平行四边形，

且，

、分别为、的中点，且，

所以，四边形为平行四边形，，

平面，平面，平面；

（2）如下图所示，取的中点，连接、，取的中点，连接、，

在正方体中，且，

、分别为、的中点，且，

所以，四边形为平行四边形，且，

同理可证四边形为平行四边形，则且，

所以，且，所以，四边形为平行四边形，

则截面图形为平行四边形，

又，则四边形为菱形，则，

且，，则菱形的面积为.

【点睛】

本题考查线面平行的证明，同时也考查了正方体截面面积的求解，考查推理能力与计算能力，属于中等题.

22．（2020·陕西咸阳市·高三二模（文））如图，在直角梯形中，，，，为的中点，沿将折起，使得点到点位置，且，为的中点，是上的动点（与点，不重合）.

（1）证明：平面平面；

（2）设三棱锥和四棱锥的体积分别为和，当为中点时，求的值.

【答案】（1）证明见解析；（2）.

【分析】

（1）利用线面垂直的判定定理和线面垂直的性质得出，再由面面垂直的判定定理证明平面平面；

（2）求出三角形和正方形的面积比，由点，到平面的距离之比，结合棱锥的体积公式，即可得出的值.

【详解】

（1）证明：∵，，，平面

∴平面

又平面，∴

，平面，

∴平面

平面

由，知

又平面，

平面

又平面，∴平面平面

（2）∵为中点

∴，

点，到平面的距离之比为

∴

【点睛】

本题主要考查了证明面面垂直以及棱锥体积的有关计算，属于中档题.