




第16讲 对数运算与对数函数-【新教材】2022新高一同步(初升高)衔接讲义(原卷+解析)
展开第16讲 对数运算与对数函数
一.对数的概念
一般地,对于指数式,我们把“以为底的对数”记作,即.其中,数叫做对数的底数,叫做真数,读作“等于以为底的对数”.
【定义理解】
训练1.将下列指数式写成对数式:
(1) ; (2).
训练2.将下列对数式写成指数式:
(1); (2) .
二.对数运算法则
(1)
(2)
(3)
(4)
(5)
例1.计算:
(1) (2) (3) (4)
(5) (6) (7)
练习1: 计算:
(1) (2) (3) (4)
(5) (6) (7)
例2.已知 , , 用表示 .
三.对数函数的概念
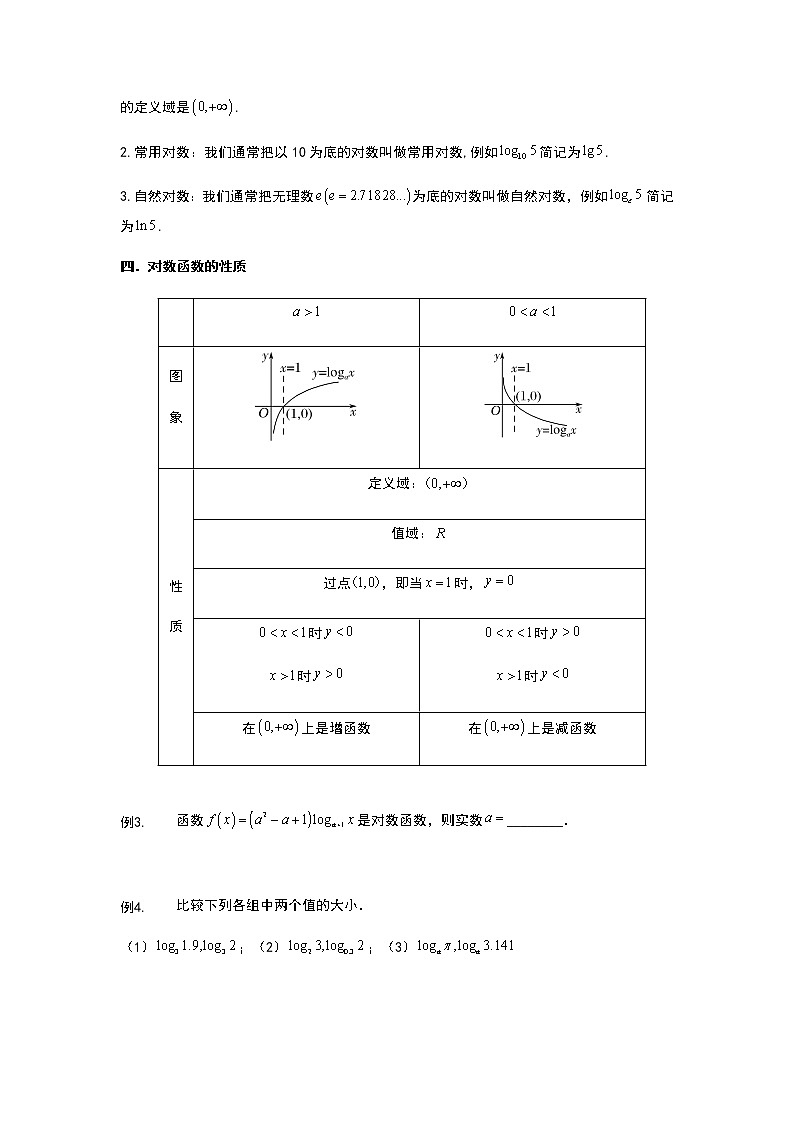
1.定义:一般地,我们把函数叫做对数函数,其中是自变量,函数的定义域是.
2.常用对数:我们通常把以10为底的对数叫做常用对数,例如简记为.
3.自然对数:我们通常把无理数为底的对数叫做自然对数,例如简记为.
四.对数函数的性质
| ||
图 象 | ||
性 质 | 定义域: | |
值域: | ||
过点,即当时, | ||
时 时 | 时 时 | |
在上是增函数 | 在上是减函数 | |
例3.函数是对数函数,则实数________.
例4.比较下列各组中两个值的大小.
(1);(2);(3)
例5.求下列函数的定义域.
(1) (2) (3)
例6.求下列函数的值域:
(1) (2)
例7.已知,求的最大值及相应的的值.
五、对数函数的图象变换及定点问题
(1)与对数函数有关的函数图象过定点问题
对数函数过定点,即对任意的对数函数都有.
(2)对数函数的图象变换的问题
①
②
③
④
例8.若函数的图象恒过定点,则实数的值分别为 .
例9.作出函数的图象.
例10. 解下列不等式:
(1); (2).
例11. 若,求实数的取值范围.
例12. 求函数的单调区间.
例13. 求函数的单调区间.
例14. 已知在上是增函数,求实数的取值范围.
例15. 判断函数的奇偶性.
例16. 已知函数.
(1)求函数的定义域;
(2)判断函数的奇偶性;
(3)求使的的取值范围.
扩充:反函数
(1)对数函数的反函数
指数函数与对数函数互为反函数.
(2)互为反函数的两个函数之间的关系
①原函数的定义域、值域分别是其反函数的值域、定义域;
②互为反函数的两个函数的图象关于直线对称.
例17. 若函数是函数的反函数,且,则( )
A. B. C. D.
例18. 函数的反函数的定义域为( )
A. B. C. D.
例19. 若函数的反函数图象过点,则函数的图象必过点( )
A. B. C. D.
跟踪训练——对数与对数运算(一)
- 对应的指数式是( )
- B. C. D.
- 下列指数式与对数式互化不正确的一组是( )
A.与 B.与
C.与 D.与
- 设,则的值等于( )
- 10 B. C.100 D.1000
- 设,则底数的值等于( )
- 2 B. C. 4 D.
- 已知,那么等于( )
- B. C. D.
- 若,则 ;若,则 .
- 计算: ; .
- 求下列各式的值:______;_______.
- 求下列各式中的取值范围:(1); (2).
- (1)设,求的值.
(2)设,且,求的值.
对数与对数运算(二)
1.( )
A.1 B. C.2 D.
2.化简得结果是( )
A. B. C. D.
3.化简的结果是( )
A. B.1 C.2 D.
4.已知, 则的值等于( )
A.1 B.2 C.8 D.12
5.化简的结果是 ( )
A.1 B. C.2 D.3
6.计算 .
7.若,则 .
8.(1)已知,试用表示的值;
(2)已知,用表示.
跟踪训练——对数函数及其性质(一)
- 下列各式错误的是( )
A. B.
C. D.
- 当时,在同一坐标系中,函数与的图象是( )
A B C D
- 下列函数中哪个与函数是同一个函数( )
A. B.
C. D.
- 函数的定义域是( )
A. B. C. D.
- 若,那么满足的条件是( )
A. B. C. D.
- 求下列函数的定义域:
(1) (2)
- 已知函数,,求:
(1) 的值域;
(2) 的最大值及相应的值.
跟踪训练——对数函数及其性质(二)
- 函数的图象关于( )
A.轴对称 B.轴对称 C.原点对称 D. 直线对称
- 函数的值域是( )
A. B. C. D.
- 设,函数在区间上的最大值与最小值之差为,则( )
A. B.2 C. D.4
- 图中的曲线是的图象,已知的值为,则曲线相应的 依次为( )
A. B.
C. D.
- 下列函数中,在上为增函数的是( )
A. B.
C. D.
- 函数是 函数.(填“奇”、“偶”或“非奇非偶”)
- 函数的反函数的图象过点,则的值为 .
- 求函数的单调区间.
- 若函数在区间上是增函数,求实数的取值范围.








