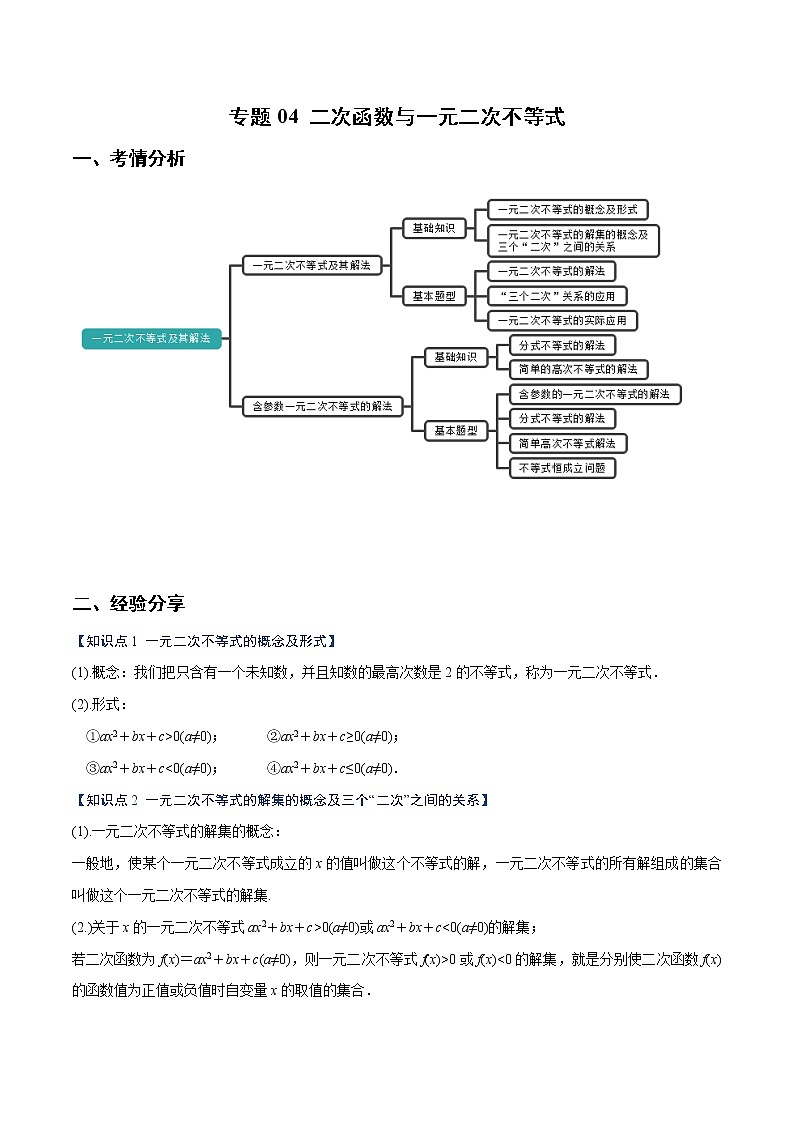

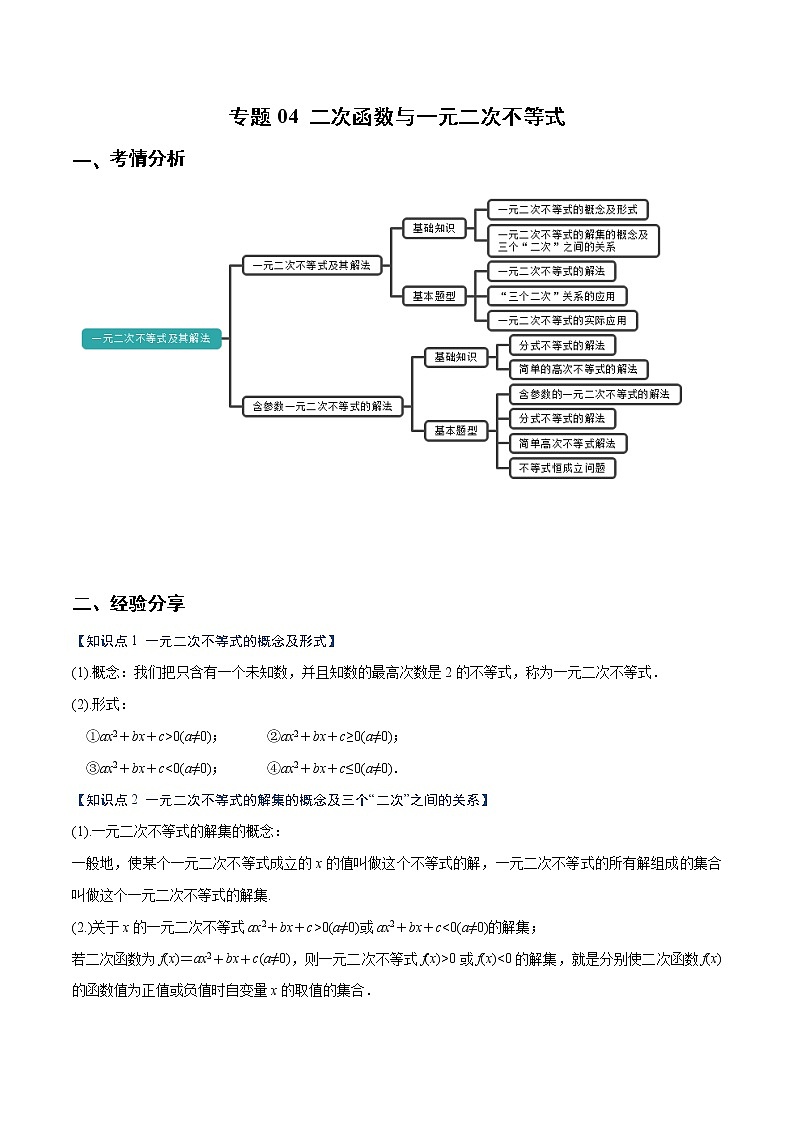

所属成套资源:2022年秋季(人教2019A版)高一上期末专题训练+精品讲义
- 专题03 等式性质与不等式性质、基本不等式(重难点突破)-【教育机构专用】2022年秋季高一上精品讲义(新教材人教A版) 其他 5 次下载
- 专题04 二次函数与一元二次不等式(课时训练)-【教育机构专用】2022年秋季高一上精品讲义(新教材人教A版) 试卷 3 次下载
- 专题05 函数的概念及其表示、分段函数(课时训练)-【教育机构专用】2022年秋季高一上精品讲义(新教材人教A版) 试卷 3 次下载
- 专题05 函数的概念及其表示、分段函数(重难点突破)-【教育机构专用】2022年秋季高一上精品讲义(新教材人教A版) 其他 4 次下载
- 专题06 函数基本性质的灵活应用(单调性与奇偶性)(课时训练)-【教育机构专用】2022年秋季高一上精品讲义(新教材人教A版) 试卷 4 次下载
专题04 二次函数与一元二次不等式(重难点突破)-【教育机构专用】2022年秋季高一上精品讲义(新教材人教A版)
展开
专题04 二次函数与一元二次不等式一、考情分析 二、经验分享【知识点1 一元二次不等式的概念及形式】(1).概念:我们把只含有一个未知数,并且知数的最高次数是2的不等式,称为一元二次不等式.(2).形式:①ax2+bx+c>0(a≠0); ②ax2+bx+c≥0(a≠0);③ax2+bx+c<0(a≠0); ④ax2+bx+c≤0(a≠0).【知识点2 一元二次不等式的解集的概念及三个“二次”之间的关系】(1).一元二次不等式的解集的概念:一般地,使某个一元二次不等式成立的x的值叫做这个不等式的解,一元二次不等式的所有解组成的集合叫做这个一元二次不等式的解集.(2.)关于x的一元二次不等式ax2+bx+c>0(a≠0)或ax2+bx+c<0(a≠0)的解集;若二次函数为f(x)=ax2+bx+c(a≠0),则一元二次不等式f(x)>0或f(x)<0的解集,就是分别使二次函数f(x)的函数值为正值或负值时自变量x的取值的集合.(3).三个“二次”之间的关系:设f(x)=ax2+bx+c(a>0),方程ax2+bx+c=0的判别式Δ=b2-4ac 判别式Δ=b2-4acΔ>0Δ=0Δ<0解不等式f(x)>0或f(x)<0的步骤求方程f(x)=0的解有两个不等的实数解x1,x2有两个相等的实数解x1=x2没有实数解画函数y=f(x)的示意图得不等式的解集f(x)>0{x|x<x1或x>x2}{x|x≠-}Rf(x)<0{x|x1<x<x2}∅∅ 【知识点3 分式不等式的解法】①>0与(x+1)(x+3)>0等价吗?②≤0与(2x-1)(x+2)≤0等价吗?定义:分母中含有未知数,且分子、分母都是关于x的多项式的不等式称为分式不等式.解法:等价转化法解分式不等式>0⇔f(x)g(x)>0,<0⇔f(x)·g(x)<0.≥0⇔⇔f(x)·g(x)>0或.≤0⇔⇔f(x)·g(x)<0或【知识点4、简单的高次不等式的解法】(1)由函数与方程的关系可知y=(x+1)(x-1)(x-2)与x轴相交于(-1,0),(1,0),(2,0)三点,试考虑当x>2,1<x<2,x<1不同情形下,y值的符号变化情况.(2)考查函数y=(x-1)2(x+3),当x<-3,-3<x<1,x>1时,y的取值正负情形.你发现了什么规律?高次不等式:不等式最高次项的次数高于2,这样的不等式称为高次不等式.解法:穿根法①将f(x)最高次项系数化为正数;②将f(x)分解为若干个一次因式的积或二次不可分因式的积;③将每一个一次因式的根标在数轴上,自上而下,从右向左依次通过每一点画曲线(注意重根情况,偶次方根穿而不过,奇次方根穿过);④观察曲线显现出的f(x)的值的符号变化规律,写出不等式的解集. 三、题型分析(一) 一元二次不等式的解法例1.(1)(2020·吉林省实验高一期中)不等式的解集为( )A.或 B.或C. D.(2)..(3).(3); 【变式训练1】.求下列不等式的解集.(1); (2);(3); (4);(5). (二) 含有参数的一元二次不等式的解法例2.(1)(2020·全国高一)函数在上是减函数,则实数a的取值范围是___________ (2)(2019·浙江省高一期末)若关于的不等式的解集是,则________,_______. (3)解关于x的不等式x2-(3a-1)x+(2a2-2)>0. 【变式训练1】.(2019·北京市第十三中学高一期中)已知函数,①函数的值域是______.②若函数在上不是单调函数,则实数的取值范围是______. 【变式训练2】.已知M是关于x的不等式2x2+(3a-7)x+3+a-2a2<0的解集,且M中的一个元素是0,求实数a的取值范围,并用a表示出该不等式的解集.
(三) 含有参数的分式不等式的解法例3.【广东省惠州市第一中学2017-2018学年数学必修5模块综合】不等式的解集是 ( )A. B. C. D. 【变式训练1】.【上海市虹口区复兴高级中学2016-2017学年高一上学期期中】不等式的解集是______.
(四)二次不等式综合问题例4.(2020·上饶中学高二期末(文))已知,若,满足,则( )A. B.C. D.
例5.(2019·海南省海口一中高二月考)若函数的定义域为,值域为,则的取值范围是( )A. B. C. D. 【变式训练1】.(2020·宁阳县第四中学高二期末)不等式对恒成立,则的取值范围为( )A. B. C. D.【变式训练2】.(2020·调兵山市第一高级中学高二月考)已知函数,(),若任意,且都有,则实数a的取值范围( )A. B. C. D.
(五) 实际应用问题例6.(2020·全国高一)某部影片的盈利额(即影片的票房收入与固定成本之差)记为,观影人数记为,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后与的函数图象.给出下列四种说法:①图(2)对应的方案是:提高票价,并提高成本;②图(2)对应的方案是:保持票价不变,并降低成本;③图(3)对应的方案是:提高票价,并保持成本不变;④图(3)对应的方案是:提高票价,并降低成本.其中,正确的说法是____________.(填写所有正确说法的编号)【变式训练1】.(2019·江苏省金陵中学高一期中)为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用新工艺,把二氧化碳转化为一种可利用的产品.已知该单位每月处理二氧化碳最少400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似表示为y=x2-200x+80000,且每处理1吨二氧化碳得到可利用的化工产品价值为100元.(1)若该单位每月成本(每月成本=每月处理成本-每月可利用的化工产品价值)支出不超过105000元,求月处理量x的取值范围.(2)该单位每月能否获利?如果能获利,求出能获得的最大利润;如果不能获利,那么国家每月至少补贴多少元,才能使该单位不亏损?
四、迁移应用1.关于x的不等式ax2+bx+2>0的解集为{x|-1<x<2},则关于x的不等式bx2-ax-2>0的解集为( )A.{x|-2<x<1} B.{x|x>2或x<-1}C.{x|x>1或x<-2} D.{x|x<-1或x>1}2.(2020·上海高三专题练习)若不等式有唯一解,则的取值为( )A.0 B.2 C.4 D.63.(2019·海南省海口一中高二月考)若函数的定义域为,值域为,则的取值范围是( )A. B. C. D.4.不等式对恒成立,则的取值范围为( )A. B. C. D. 5.(2019·广东省增城中学高一期中)如图所示,用总长为定值l的篱笆围成长方形的场地,以墙为一边,并用平行于一边的篱笆隔开.(1)设场地面积为y,垂直于墙的边长为x,试用解析式将y表示成x的函数,并确定这个函数的定义域;(2)怎样围才能使得场地的面积最大?最大面积是多少?





