专题12 三角函数的图像与性质（正弦函数、余弦函数和正切函数）（课时训练）-【教育机构专用】2022年秋季高一上精品讲义（新教材人教A版）

这是一份专题12 三角函数的图像与性质（正弦函数、余弦函数和正切函数）（课时训练）-【教育机构专用】2022年秋季高一上精品讲义（新教材人教A版），文件包含专题12三角函数的图像与性质正弦函数余弦函数和正切函数课时训练解析版docx、专题12三角函数的图像与性质正弦函数余弦函数和正切函数课时训练原卷版docx等2份试卷配套教学资源，其中试卷共43页， 欢迎下载使用。
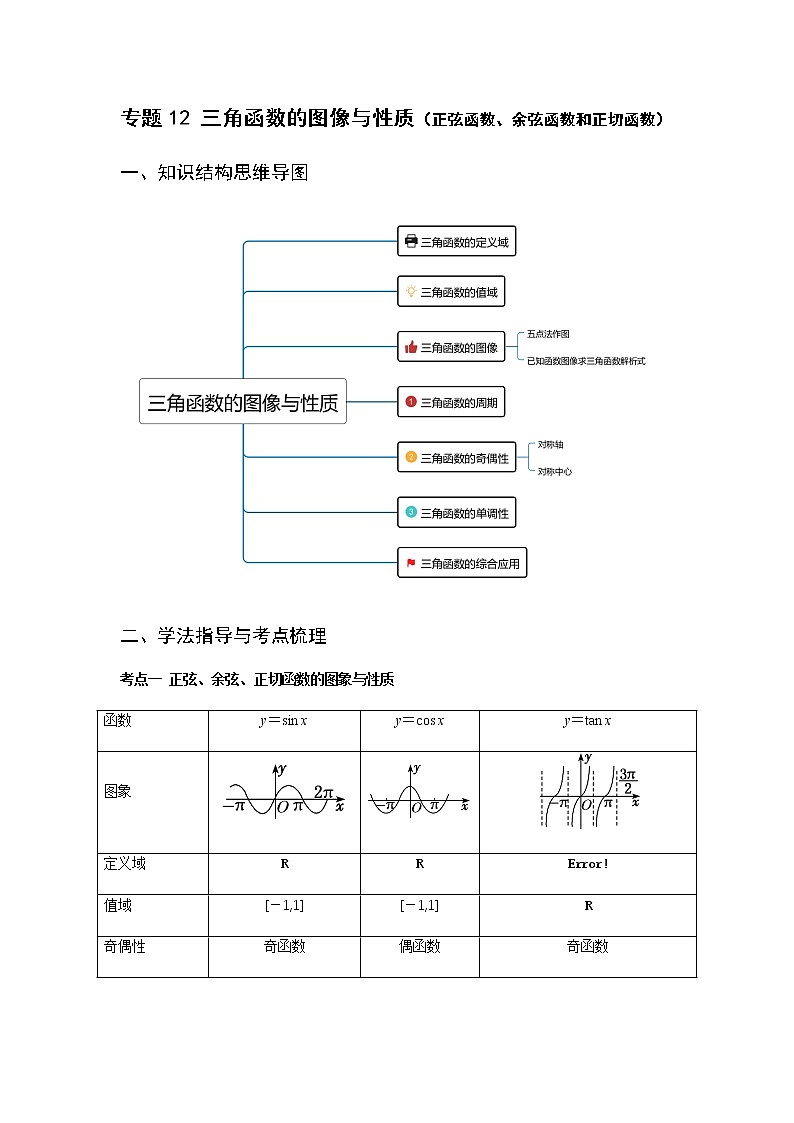
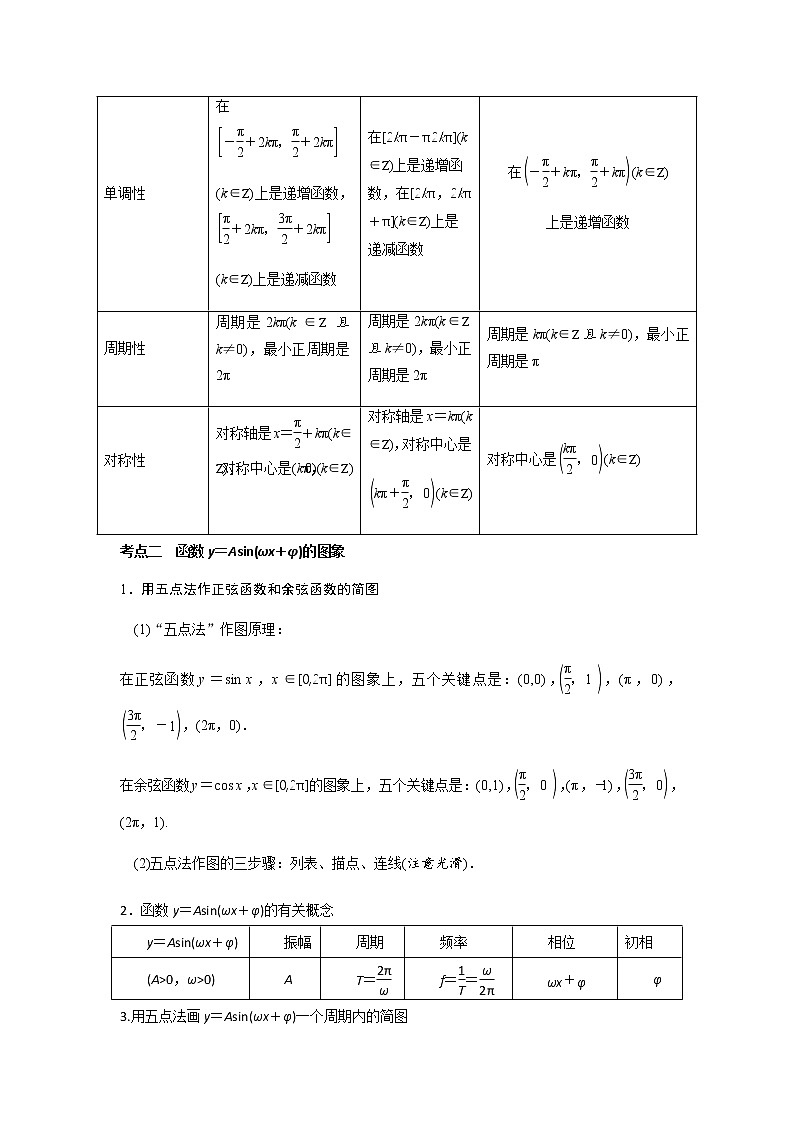
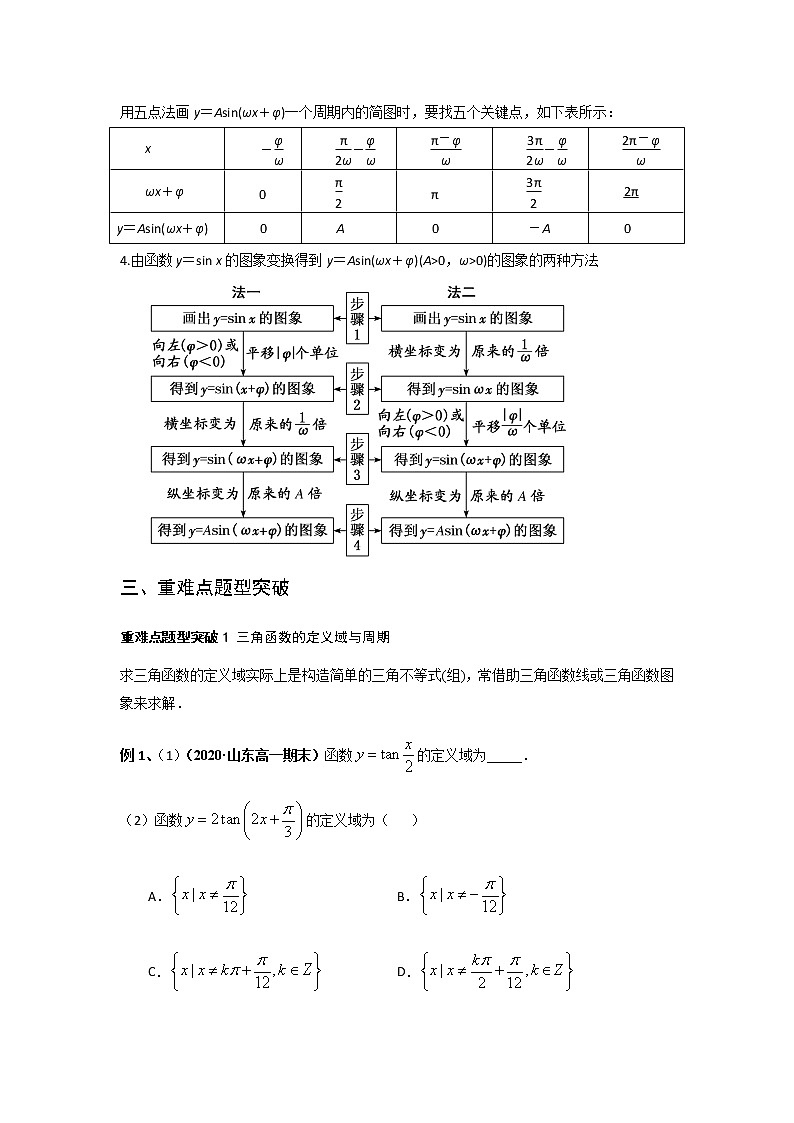
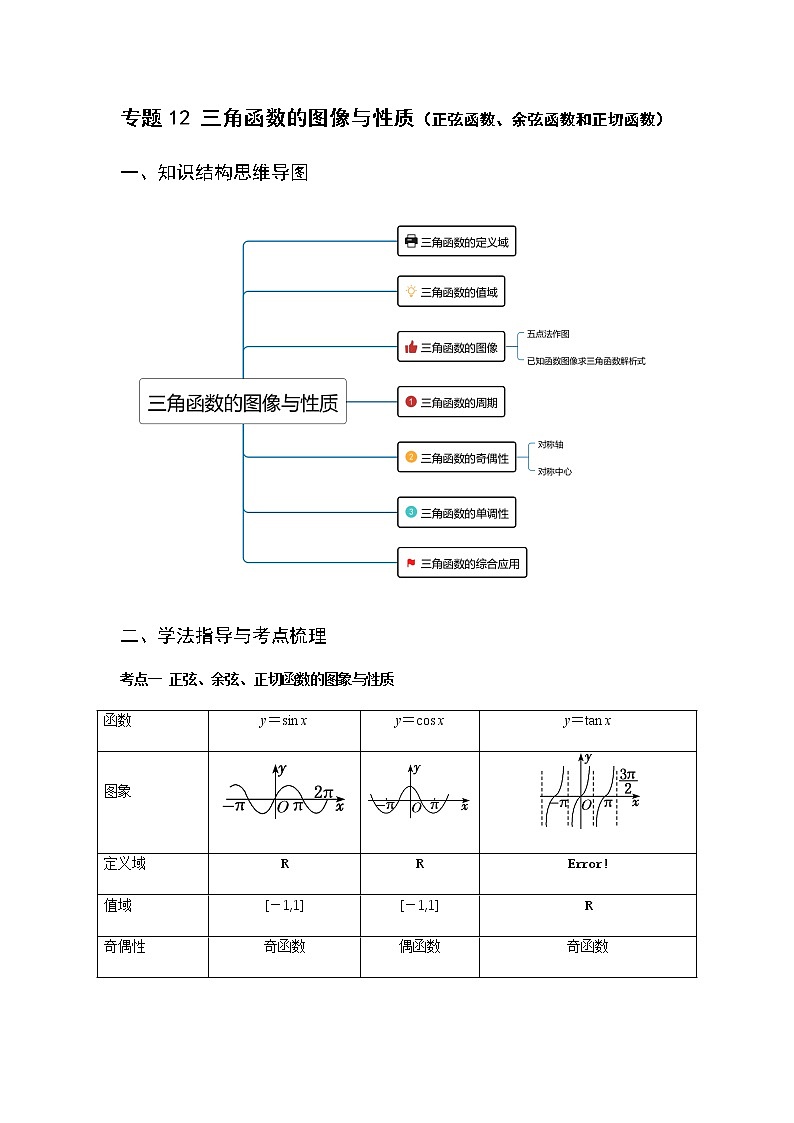
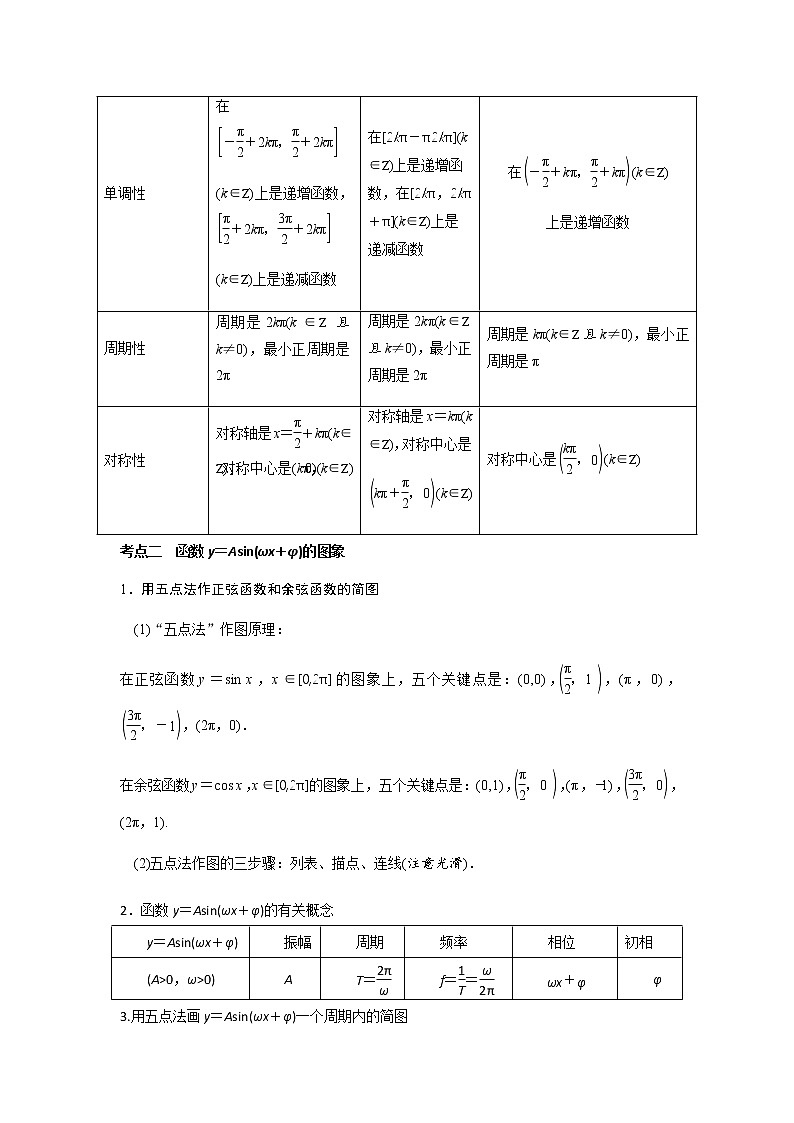
专题12 三角函数的图像与性质（正弦函数、余弦函数和正切函数）一、知识结构思维导图二、学法指导与考点梳理考点一 正弦、余弦、正切函数的图象与性质函数y＝sin xy＝cos xy＝tan x图象定义域RR值域[－1,1][－1,1]R奇偶性奇函数偶函数奇函数单调性在(k∈Z)上是递增函数，(k∈Z)上是递减函数在[2kπ－π2kπ](k∈Z)上是递增函数，在[2kπ，2kπ＋π](k∈Z)上是递减函数在(k∈Z)上是递增函数　　　　周期性周期是2kπ(k∈Z且k≠0)，最小正周期是2π周期是2kπ(k∈Z且k≠0)，最小正周期是2π周期是kπ(k∈Z且k≠0)，最小正周期是π对称性对称轴是x＝＋kπ(k∈Z)，对称中心是(kπ，0)(k∈Z)对称轴是x＝kπ(k∈Z)，对称中心是(k∈Z)对称中心是(k∈Z)考点二  函数y＝Asin(ωx＋φ)的图象1．用五点法作正弦函数和余弦函数的简图(1)“五点法”作图原理：在正弦函数y＝sin x，x∈[0,2π]的图象上，五个关键点是：(0,0)，，(π，0)，，(2π，0)．在余弦函数y＝cos x，x∈[0,2π]的图象上，五个关键点是：(0,1)，，(π，－1)，，(2π，1). (2)五点法作图的三步骤：列表、描点、连线(注意光滑)．2．函数y＝Asin(ωx＋φ)的有关概念y＝Asin(ωx＋φ)振幅周期频率相位初相(A>0，ω>0)AT＝f＝＝φ3.用五点法画y＝Asin(ωx＋φ)一个周期内的简图用五点法画y＝Asin(ωx＋φ)一个周期内的简图时，要找五个关键点，如下表所示：x－－－ωx＋φ2πy＝Asin(ωx＋φ)0A0－A04.由函数y＝sin x的图象变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种方法三、重难点题型突破重难点题型突破1 三角函数的定义域与周期求三角函数的定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．例1、（1）（2020·山东高一期末）函数的定义域为_____．（2）函数的定义域为（   ）A． B．C． D．【变式训练1-1】（2020·全国高一课时练习）求下列函数的定义域.（1）；（2）.
例2、（2020·上海市七宝中学期中）函数，的最小正周期是（    ）A．12 B．6 C． D．【变式训练2-1】、（2020·山西运城·月考）函数，的最小正周期为（    ）A． B． C． D．4  重难点题型突破2 三角函数的单调性及最值1、三角函数单调性的求法(1)形如y＝Asin(ωx＋φ)的函数的单调性问题，一般是将ωx＋φ看成一个整体，再结合图象利用y＝sin x的单调性求解；(2)如果函数中自变量的系数为负值，要根据诱导公式把自变量系数化为正值，再确定其单调性．2、求解三角函数的值域(最值)常见到以下几种类型(1)形如y＝asin x＋bcos x＋c的三角函数化为y＝Asin(ωx＋φ)＋c的形式，再求值域(最值)．(2)形如y＝asin2x＋bsin x＋c的三角函数，可先设sin x＝t，化为关于t的二次函数求值域(最值)．(3)形如y＝asin3x＋bsin2x＋csin x＋d，类似于(2)进行换元，然后用导数法求最值．　例3、（1）（2020·河南林州一中高一月考）函数的值域________．（2）．（2020·上海高一课时练习）函数，当_________时有最小值，最小值是___________.
【变式训练3-1】、函数y＝cos的单调递减区间为___． 【变式训练3-2】、已知函数最小正周期为，图象过点.（1）求函数解析式（2）求函数的单调递增区间.
重难点题型突破3 三角函数的对称性（奇函数、偶函数与对称轴、对称中心）1.奇偶性的判断方法：三角函数中奇函数一般可化为y＝Asin ωx或y＝Atan ωx的形式，而偶函数一般可化为y＝Acos ωx＋b的形式．　 2.函数具有奇偶性的充要条件函数y＝Asin(ωx＋φ)(x∈R)是奇函数⇔φ＝kπ(k∈Z)；函数y＝Asin(ωx＋φ)(x∈R)是偶函数⇔φ＝kπ＋(k∈Z)；函数y＝Acos(ωx＋φ)(x∈R)是奇函数⇔φ＝kπ＋(k∈Z)；函数y＝Acos(ωx＋φ)(x∈R)是偶函数⇔φ＝kπ(k∈Z)．例4、（1）(2020·南开区模拟)函数f(x)＝的最小正周期为(　　)A.  B. C．π  D．2π（2）已知函数f(x)＝3sin(2x－＋φ)，φ∈(0，π)．(1)若f(x)为偶函数，则φ＝________；(2)若f(x)为奇函数，则φ＝________.  【变式训练4-1】（2020·镇原中学高一期末）若点是函数的图象的一个对称中心，且点到该图象的对称轴的距离的最小值为，则（ ）A．的最小正周期是 B．的值域为C．的初相 D．在上单调递增【变式训练4-2】函数的图像的一条对称轴方程为（）A． B． C． D．【变式训练4-3】设函数f(x)＝cos，则下列结论错误的是(　　)A．f(x)的一个周期为－2π           B．y＝f(x)的图象关于直线x＝对称C．f(x＋π)的一个零点为x＝        D．f(x)在上单调递减重难点题型突破4 三角函数的图像及其应用例5．（多选题）函数的部分图像如图所示，则下列结论正确的是（    ）A． B．C．是函数的一条对称轴 D．是函数的对称轴心【变式训练5-1】（2020·海南枫叶国际学校高一期中）函数=的部分图像如图所示，则的单调递减区间为（ ）A． B．C． D．
【变式训练5-2】如图是函数在一个周期内的图象，则其解析式是（　　）A． B．C． D．【变式训练5-3】（2019·江门市第二中学期中）已知函数．（1）求函数的最小值和最大值及相应自变量x的集合；（2）求函数的单调递增区间；（3）画出函数区间内的图象．
例6．将函数y＝sin x的图象上所有的点向右平移个单位长度，再把各点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象的函数解析式是(　　)A．y＝sin B．y＝sinC．y＝sin D．y＝sin【变式训练6-1】、（多选题）若将函数的图象向左平移个单位长度，得到函数的图象，则下列说法正确的是（    ）A．的最小正周期为 B．在区间上单调递减C．不是函数图象的对称轴 D．在上的最小值为【变式训练6-2】(本小题满分12分)已知函数f（x）＝sin（π﹣ωx）cosωx+cos2ωx（ω＞0）的最小正周期为π．[来源:学科网]（1）求ω的值；（2）将函数y＝f（x）的图象上各点的横坐标缩短到原来的，纵坐标不变，得到函数y＝g（x）的图象，求函数g（x）在区间[0，]上的最小值．        
四、课堂定时训练（45分钟）1．函数图像的一条对称轴方程为（）A． B． C． D．2．如图是函数在一个周期内的图象，则其解析式是（　　）A． B．C． D．3．已知函数，则下列结论不正确的是（    ）A.是的一个周期 B.C.的值域为R D.的图象关于点对称4．函数的定义域是（　　）A. B.C. D.5．（2019·湖南武冈市第一中学高一期中）下列函数中，最小正周期为的是（  ）A． B． C． D．5．（多选题）将函数y＝4sin x的图象向左平移个单位长度，再将横坐标缩短到原来的，得到函数y＝f(x)的图象，下列关于y＝f(x)的说法正确的是(　　)[来源:Z#xx#k.Com]A．y＝f(x)的最小正周期为4πB．由f(x1)＝f(x2)＝0可得x1－x2是π的整数倍[来源:学#科#网Z#X#X#K][来源:学&科&网]C．y＝f(x)的表达式可改写成f(x)＝4cos D．y＝f(x)的图象关于中心对称6．（2019·浙江高一期末）已知函数，则的最小正周期是______；的对称中心是______．7．（2019·浙江高一期末）函数的最小正周期为_____；单调递增区间为_______．8．（2019·宁夏高一期末）函数的最大值为，最小值为，则的最小正周期为______.9．（2018·内蒙古一机一中高一月考（理））已知函数（1）用五点法作出函数的简图；（2）写出函数的值域与单调区间.
10．已知函数.(1)求函数的最大值以及相应的x的取值集合；(2)若直线是函数的图像的对称轴，求实数m的值.