专题14 三角恒等变换、三角函数的应用（课时训练）-【教育机构专用】2022年秋季高一上精品讲义（新教材人教A版）

这是一份专题14 三角恒等变换、三角函数的应用（课时训练）-【教育机构专用】2022年秋季高一上精品讲义（新教材人教A版），文件包含专题14三角恒等变换三角函数的应用课时训练解析版docx、专题14三角恒等变换三角函数的应用课时训练原卷版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
专题14 三角恒等变换、三角函数的应用【基础巩固】1．（2020届四川省成都市高三第二次诊断）已知锐角满足则（    ）A． B． C． D．2．（2020届山西省大同市第一中学高三一模）已知，，则等于（    ）．A． B． C． D．3．（2020·浙江高一课时练习）如图所示为一质点做简谐运动的图象，则下列判断中正确的是（    ）A．该质点的振动周期为 B．该质点的振幅为C．该质点在和时振动速度最大 D．该质点在和时的振动速度为04．（2020届百校联考高考考前冲刺）已知为坐标原点，角的终边经过点且，则(    )A． B． C． D．5．（2020届甘肃省兰州市高三诊断）已知函数（），若函数的图象与直线在上有3个不同的交点，则的取值范围是（    ）A． B．C． D．6．（2020·北京市平谷区高三一模）已知，那么______.7．（2020届百校联考高考考前冲刺）若，则____.8．已知函数f（x）＝sin（2x）+1．（1）用“五点法”作出f（x）在上的简图；（2）写出f（x）的对称中心以及单调递增区间；（3）求f（x）的最大值以及取得最大值时x的集合．
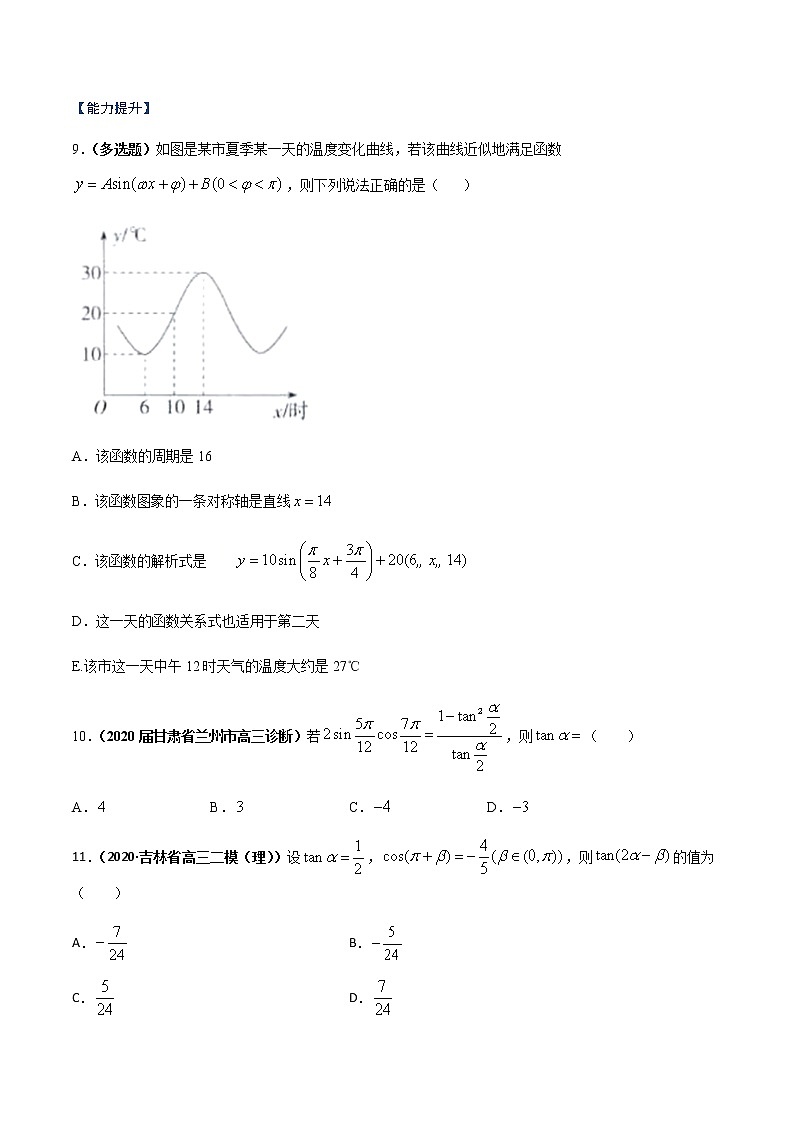
【能力提升】9．（多选题）如图是某市夏季某一天的温度变化曲线，若该曲线近似地满足函数，则下列说法正确的是（    ）A．该函数的周期是16B．该函数图象的一条对称轴是直线C．该函数的解析式是D．这一天的函数关系式也适用于第二天E.该市这一天中午12时天气的温度大约是27℃10．（2020届甘肃省兰州市高三诊断）若，则（    ）A． B． C． D．11．（2020·吉林省高三二模（理））设，，则的值为（    ）A． B．C． D．12．（2020届安徽省“江南十校”高三综合素质检测）已知.给出下列判断：①若，且，则；②存在使得的图象向右平移个单位长度后得到的图象关于轴对称；③若在上恰有7个零点，则的取值范围为；④若在上单调递增，则的取值范围为.其中，判断正确的个数为（    ）A．1 B．2 C．3 D．413．（2020·辉县市第二高级中学高一期中）已知某海滨浴场海浪的高度y（米）是时间t的（0≤t≤24，单位：小时）函数，记作y=f（t），下表是某日各时的浪高数据：t（h）03691215182124y（m）1.51.00.51.01.51.00.50.991.5经长期观测，y=f（t）的曲线可近似地看成是函数y=Acosωt＋b的图象．（1）根据以上数据，求出函数y=Acosωt＋b的最小正周期T、振幅A及函数表达式； （2）依据规定，当海浪高度高于1米时才对冲浪爱好者开放，请依据（1）的结论，判断一天内的上午8时到晚上20时之间，有多长时间可供冲浪者进行运动？
14．（2020·黄梅国际育才高级中学高一期中）已知0<α<<β<π,cos,sin(α+β)=.(1)求sin 2β的值;(2)求cos的值.
15．已知函数.（1）求的最小正周期；（2）当时，求的值域.