第四讲 集合之间的关系（二）-【暑假辅导班】2022年新高一年级数学暑假精品课程（人教A版2019） 试卷

第四讲：集合之间的关系（二）

【学习目标】

1．能用子集和真子集的概念，判断集合之间的关系，并用符号或Venn图表示；

2.根据集合之间的关系，求解出参数的取值范围.

【基础知识】

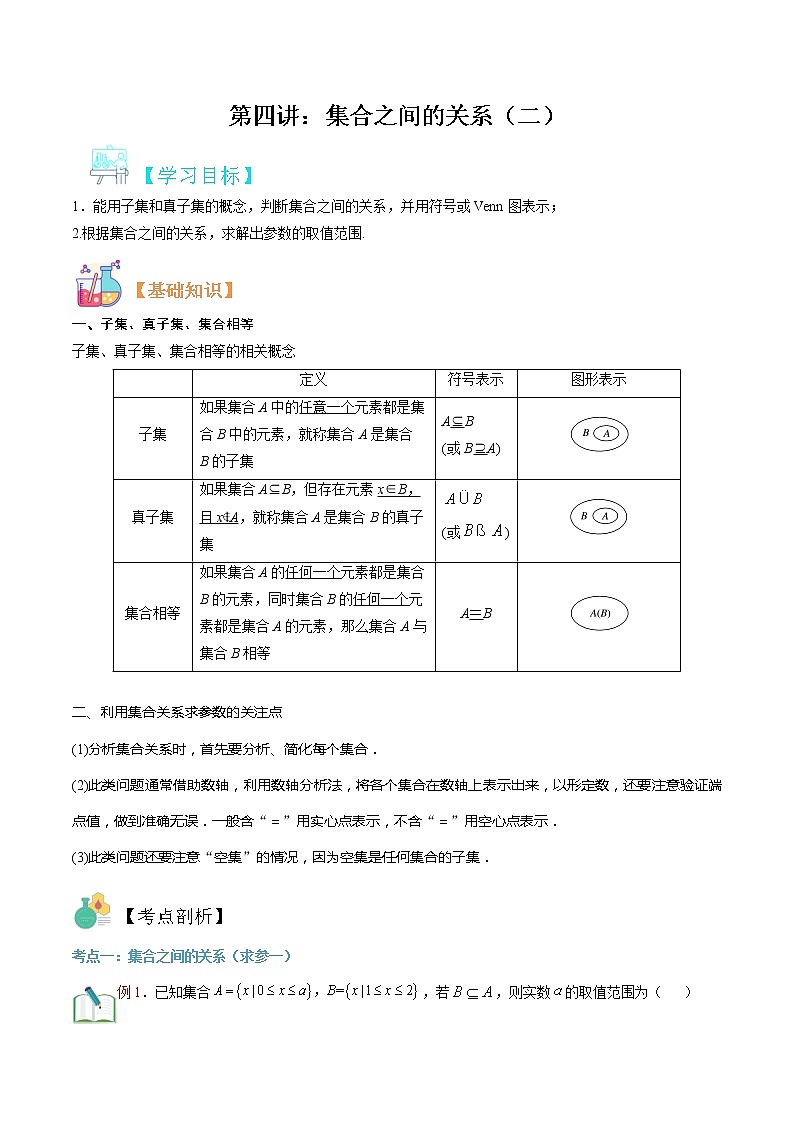
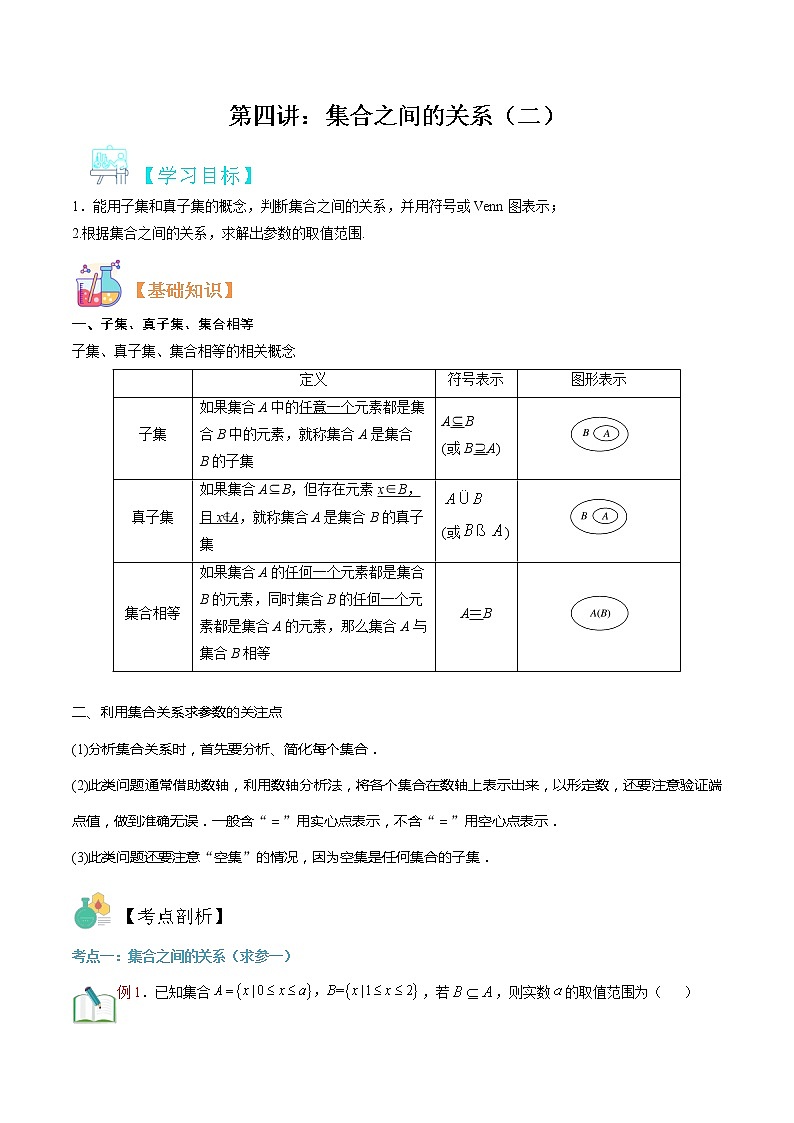
一、子集、真子集、集合相等

子集、真子集、集合相等的相关概念

二、利用集合关系求参数的关注点

(1)分析集合关系时，首先要分析、简化每个集合．

(2)此类问题通常借助数轴，利用数轴分析法，将各个集合在数轴上表示出来，以形定数，还要注意验证端点值，做到准确无误．一般含“＝”用实心点表示，不含“＝”用空心点表示．

(3)此类问题还要注意“空集”的情况，因为空集是任何集合的子集．

【考点剖析】

考点一：集合之间的关系（求参一）

例1．已知集合，若，则实数的取值范围为（   ）

 A． B． C． D．

变式训练1：已知集合，则=（   ）

 A．或 B．或3 C．1或 D．1或3

变式训练2：已知集合，，若，则（   ）

 A．-3 B．-2 C．3 D．-2或3

变式训练3：已知，若，则实数的取值范围（   ）

 A． B． C． D．

考点二：集合之间的关系（求参二）

例2．已知，，若，则实数取值的集合为（   ）

 A． B． C． D．

变式训练1：已知集合，集合，若，则实数的值是（   ）

 A．0 B． C．0或 D．0或

变式训练2：若集合，，且，则实数取值的集合为（    ）

 A． B． C． D．

变式训练3：当两个集合中有一个集合为另一一集合的子集时称这两个集合之间构成“全食”，当两个集合有公共元素，但互不为对方子集时称两集合之间构成“偏食”.对于集合，，若与构成“全食”，或构成“偏食”，则的取值集合为___________.

考点二：集合之间的关系（求参三）

例2．已知集合，集合，若，则的取值范围为（    ）

 A．  B．

 C． D．

变式训练1：已知集合或，，且，则实数的取值范围为（   ）

 A． B．

 C． D．

变式训练2：设，，若，则实数的取值范围是（    ）

 A． B．

 C．  D．

变式训练3：已知集合，，若，则实数的取值范围是________．

【当堂小结】

1．知识清单：

(1)由集合间的关系求参数的值或范围．

2．方法归纳：数形结合、分类讨论．

3．常见误区：忽略对集合是否为空集的讨论，忽视是否能够取到端点．

【过关检测】

1、已知集合，，若，则实数的取值范围是（   ）

 A． B． C． D．

2、已知集合，，若，则由实数的所有可能的取值组成的集合为（   ）

 A． B． C． D．

3、已知集合，，若，则实数________.

4、若一个集合是另一个集合的子集，则称两个集合构成“鲸吞”；若两个集合有公共元素，且互不为对方子集，则称两个集合构成“蚕食”，对于集合，，若这两个集合构成“鲸吞”或“蚕食”，则的取值集合为______．

5、已知，，，则范围____________.

6、已知集合.若，则实数的取值范围为_________.

7、已知集合，且.

（1）求集合；

（2）如果集合，且，求的值组成的集合.

8、已知集合.

（1）若，，求实数的取值范围；

（2）若，，求实数的取值范围；