高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.4 空间点、直线、平面之间的位置关系导学案

这是一份高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.4 空间点、直线、平面之间的位置关系导学案，文件包含841平面原卷版docx、841平面解析版docx等2份学案配套教学资源，其中学案共36页， 欢迎下载使用。

 8.4.1平面
导学案
编写：廖云波 初审：谭光垠 终审：谭光垠 廖云波
【学习目标】
1.掌握平面的表示法，点、直线与平面的位置关系
2.掌握有关平面的三个公理
3.会用符号表示图形中点、直线、平面之间的位置关系
【自主学习】
知识点1 平面
(1)平面的概念
①平面是一个不加定义，只需理解的原始概念．
②立体几何里的平面是从呈平面形的物体中抽象出来的．如课桌面、黑板面、平静的水面等都给我们平面的局部形象．
(2)平面的画法
常常把水平的平面画成一个平行四边形，并且其锐角画成45°，且横边长等于邻边长的2倍.

一个平面被另一个平面遮挡住，为了增强立体感，被遮挡部分用虚线画出来.


(3)平面的表示方法
①用希腊字母表示，如平面α，平面β，平面γ.
②用表示平面的平行四边形的四个顶点的大写字母表示，如平面ABCD.
③用表示平面的平行四边形的相对的两个顶点表示，如平面AC，平面BD.

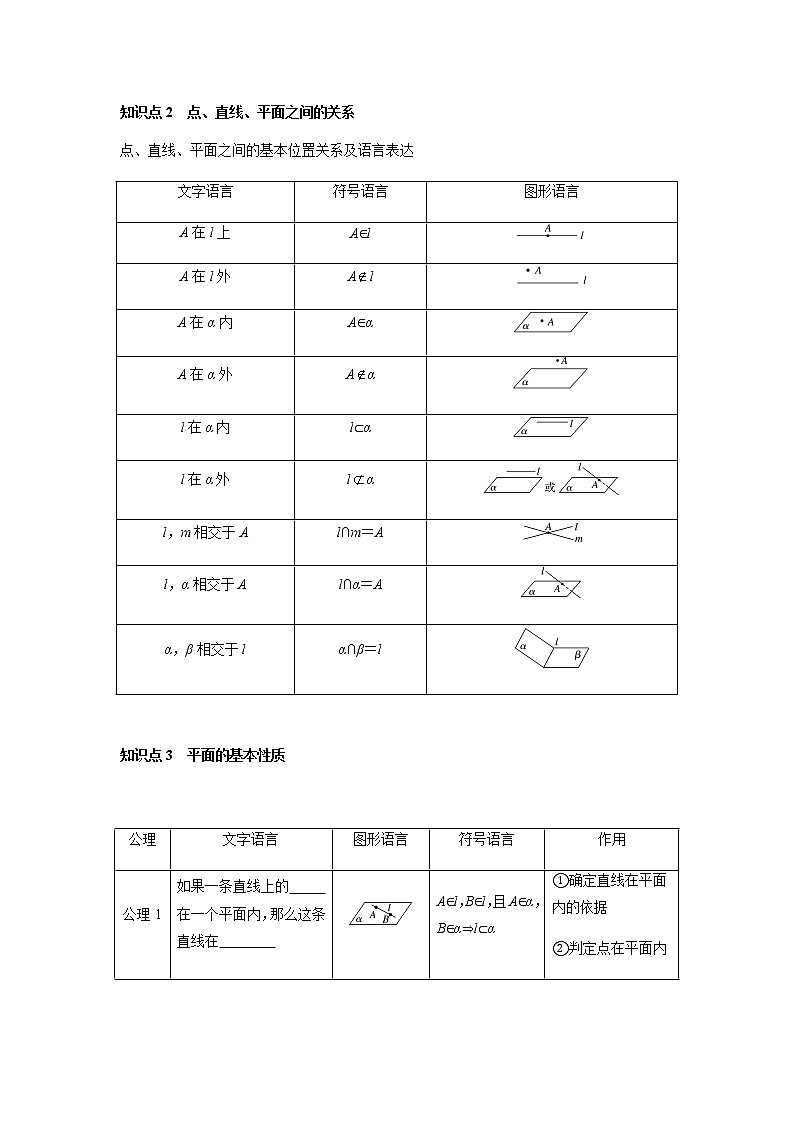
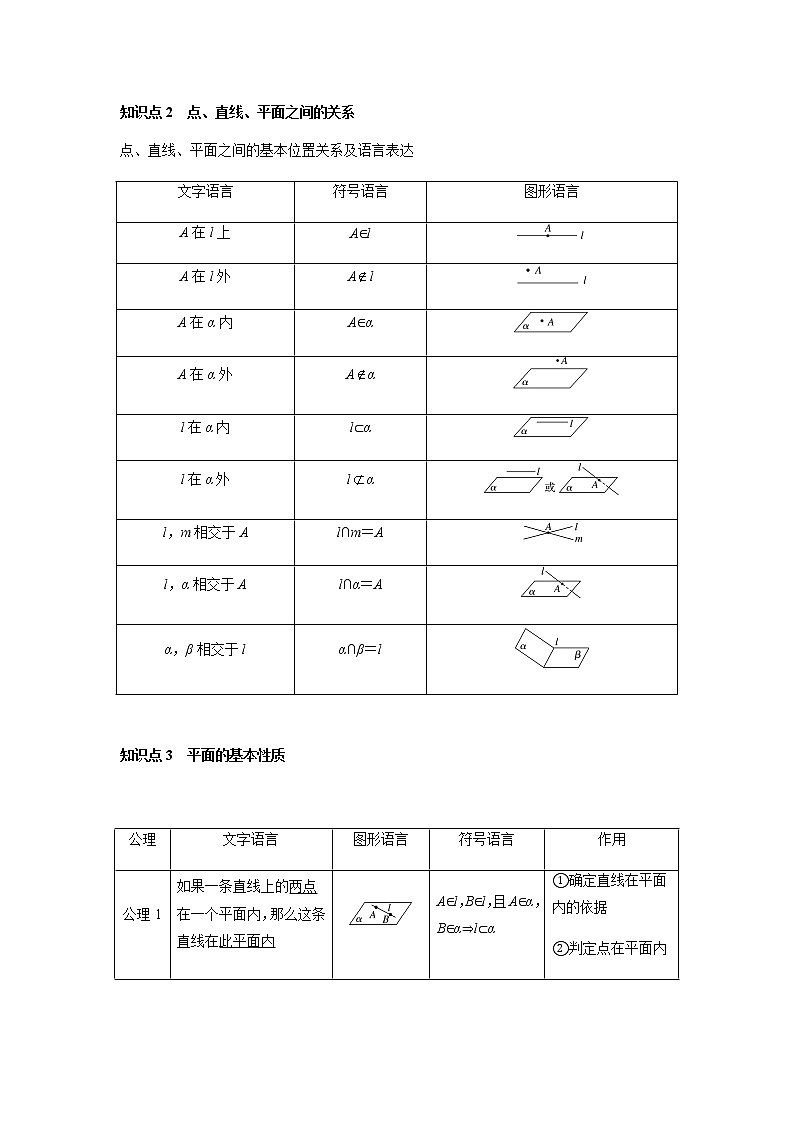
知识点2 点、直线、平面之间的关系
点、直线、平面之间的基本位置关系及语言表达
文字语言
符号语言
图形语言
A在l上
A∈l

A在l外
Al

A在α内
A∈α

A在α外
Aα

l在α内
l⊂α

l在α外
lα

l，m相交于A
l∩m＝A

l，α相交于A
l∩α＝A

α，β相交于l
α∩β＝l


知识点3 平面的基本性质

公理
文字语言
图形语言
符号语言
作用
公理1
如果一条直线上的两点在一个平面内，那么这条直线在此平面内

A∈l，B∈l，且A∈α，B∈α⇒l⊂α
①确定直线在平面内的依据
②判定点在平面内
公理2
过不在一条直线上的三点，有且只有一个平面

A，B，C三点不共线⇒存在唯一的平面α使A，B，C∈α
①确定平面的依据
②判定点线共面
公理3
如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线

P∈α且P∈β⇒α∩β＝l，且P∈l
①判定两平面相交的依据
②判定点在直线上

【合作探究】
探究一 点、直线、平面之间的位置关系的符号表示
【例1】如图，用符号表示下列图形中点、直线、平面之间的位置关系．

解　在(1)中，α∩β＝l，a∩α＝A，a∩β＝B.
在(2)中，α∩β＝l，a⊂α，b⊂β，a∩l＝P，b∩l＝P.

归纳总结：(1)用文字语言、符号语言表示一个图形时，首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何，试着用文字语言表示，再用符号语言表示.
(2)要注意符号语言的意义.如点与直线的位置关系只能用“∈”或“∉”，直线与平面的位置关系只能用“⊂”或“⊄”.


【练习1】根据下列符号表示的语句，说明点、线、面之间的位置关系，并画出相应的图形：(1)A∈α，B∉α；(2)l⊂α，m∩α＝A，A∉l；(3)平面ABD∩平面BDC＝BD，平面ABC∩平面ADC＝AC.
解　(1)点A在平面α内，点B不在平面α内，如图①.
(2)直线l在平面α内，直线m与平面α相交于点A，且点A不在直线l上，如图②.
(3)平面ABD与平面BDC相交于BD，平面ABC与平面ADC相交于AC，如图③.



探究二 点线共面
【例2】如图，已知：a⊂α，b⊂α，a∩b＝A，P∈b，PQ∥a，求证：PQ⊂α.

证明　因为PQ∥a，所以PQ与a确定一个平面β.所以直线a⊂β，点P∈β.因为P∈b，b⊂α，所以P∈α.又因为a⊂α，所以α与β重合，所以PQ⊂α.

归纳总结：证明点、线共面的两种方法
方法一：先由确定平面的条件确定一个平面，然后再证明其他的点、线在该平面内．
方法二：先由有关点、线确定一个平面α，再由其余元素确定一个平面β，然后根据有关定理，证明这两个平面重合

【练习2】已知：如图所示，l1∩l2＝A，l2∩l3＝B，l1∩l3＝C.求证：直线l1，l2，l3在同一平面内．

证明　方法一　(纳入平面法)
∵l1∩l2＝A，∴l1和l2确定一个平面α.
∵l2∩l3＝B，∴B∈l2.
又∵l2⊂α，∴B∈α.同理可证C∈α.
∵B∈l3，C∈l3，∴l3⊂α.
∴直线l1，l2，l3在同一平面内．
方法二　(辅助平面法)
∵l1∩l2＝A，∴l1和l2确定一个平面α.
∵l2∩l3＝B，∴l2，l3确定一个平面β.
∵A∈l2，l2⊂α，∴A∈α.
∵A∈l2，l2⊂β，∴A∈β.
同理可证B∈α，B∈β，C∈α，C∈β.
∴不共线的三个点A，B，C既在平面α内，又在平面β内．
∴平面α和β重合，即直线l1，l2，l3在同一平面内．


探究三 点共线、线共点问题
【例3】如图所示，在正方体ABCD－A1B1C1D1中，E为AB的中点，F为AA1的中点．求证：CE、D1F，DA三线交于一点．

证明　如图，连接EF，D1C，A1B.

∵E为AB的中点，F为AA1的中点，∴EF綊A1B.
又∵A1B綊D1C，
∴EF綊D1C，
∴E，F，D1，C四点共面，
∴D1F与CE相交，设交点为P.
又D1F⊂平面A1D1DA，CE⊂平面ABCD，
∴P为平面A1D1DA与平面ABCD的公共点．
又平面A1D1DA∩平面ABCD＝DA，
根据公理3，可得P∈DA，
即CE、D1F、DA相交于一点．

归纳总结：
(1)证明三点共线的常用方法：
方法一：首先找出两个平面，然后证明这三点都是这两个平面的公共点.根据基本事实3知，这些点都在交线上.
方法二：选择其中两点确定一条直线，然后证明另一点也在其上.
(2)证明三线共点的思路是：先证两条直线交于一点，再证明第三条直线经过这点，把问题转化为证明点在直线上的问题.


【练习3】已知△ABC在平面α外，其三边所在的直线满足AB∩α＝P，BC∩α＝Q，AC∩α＝R，如图所示．求证：P，Q，R三点共线．

证明　方法一　∵AB∩α＝P，
∴P∈AB，P∈平面α.
又AB⊂平面ABC，∴P∈平面ABC.
∴由公理3可知：点P在平面ABC与平面α的交线上，
同理可证Q、R也在平面ABC与平面α的交线上．
∴P、Q、R三点共线．
方法二　∵AP∩AR＝A，
∴直线AP与直线AR确定平面APR.
又∵AB∩α＝P，AC∩α＝R，
∴平面APR∩平面α＝PR.
∵B∈平面APR，C∈平面APR，
∴BC⊂平面APR.
∵Q∈BC，∴Q∈平面APR，
又Q∈α，∴Q∈PR，
∴P、Q、R三点共线．




课后作业
A组 基础题
一、选择题
1．下列四个选项中的图形表示两个相交平面，其中画法正确的是(　　)

【答案】　D
解析　画两个相交平面时，被遮住的部分用虚线表示．
2．空间中，可以确定一个平面的条件是(　　)
A．三个点 B．四个点
C．三角形 D．四边形
【答案】　C
解析　由平面的基本性质及推论得：在A中，不共线的三个点能确定一个平面，共线的三个点不能确定一个平面，故A错误；在B中，不共线的四个点最多能确定四个平面，故B错误；在C中，由于三角形的三个顶点不共线，因此三角形能确定一个平面，故C正确；在D中，四边形有空间四边形和平面四边形，空间四边形不能确定一个平面，故D错误．故选C.
3．如果A点在直线a上，而直线a在平面α内，点B在α内，可以表示为(　　)
A．A⊂a，a⊂α，B∈α B．A∈a，a⊂α，B∈α
C．A⊂a，a∈α，B⊂α D．A∈a，a∈α，B∈α
【答案】　B
解析　A点在直线a上，而直线a在平面α内，点B在α内，表示为：A∈a，a⊂α，B∈α，故选B.
4．空间四点A、B、C、D共面而不共线，那么这四点中(　　)
A．必有三点共线 B．必有三点不共线
C．至少有三点共线 D．不可能有三点共线
【答案】　B
解析　A、B、C、D共面而不共线，这四点可能有三点共线，也可能任意三点不共线，A错误；如果四点中没有三点不共线，则四点共线，矛盾，故B正确；当任意三点不共线时，也满足条件，故C错误，当其中三点共线，第四个点不共线时，也满足条件，故D错误，故选B.
5．有下列说法：
①梯形的四个顶点在同一个平面内；
②三条平行直线必共面；
③有三个公共点的两个平面必重合．
其中正确的个数是(　　)
A．0 B．1 C．2 D．3
【答案】　B
解析　因为梯形的上下底互相平行，所以梯形是平面图形，故①正确；三条平行直线不一定共面，如三棱柱的三条侧棱，故②错误；若两个平面的三个公共点不共线，则两平面重合，若三个公共点共线，两平面有可能相交，故③错误，故选B.
6．三条两两相交的直线最多可确定的平面的个数为(　　)
A．1 B．2 C．3 D．无数
【答案】　C
解析　在空间中，两两相交的三条直线最多可以确定3个平面，如图所示：

PA、PB、PC相交于一点P，则PA、PB、PC不共面，则PA、PB确定一个平面PAB，PB、PC确定一个平面PBC，PA、PC确定一个平面PAC.故选C.
7.如图所示，平面α∩β＝l，A、B∈α，C∈β，且C∉l，直线AB∩l＝M，过A，B，C三点的平面记作γ，则γ与β的交线必通过(　　)

A．点A B．点B
C．点C但不过点M D．点C和点M
【答案】　D
解析　∵AB⊂γ，M∈AB，∴M∈γ.
又α∩β＝l，M∈l，∴M∈β.
根据公理3可知，M在γ与β的交线上．
同理可知，点C也在γ与β的交线上．
二、填空题
8．三条平行直线最多能确定的平面的个数为________．
【答案】　3
解析　当三条平行直线在一个平面内时，可以确定1个平面；当三条平行直线不在同一平面上时，可以确定3个平面．综上最多可确定3个平面．
9．设平面α与平面β相交于l，直线a⊂α，直线b⊂β，a∩b＝M，则M________l.
【答案】　∈
解析　因为a∩b＝M，a⊂α，b⊂β，所以M∈α，M∈β.又因为α∩β＝l，所以M∈l.
10．已知A∈α，B∉α，若A∈l，B∈l，那么直线l与平面α有________个公共点．
【答案】　1
解析　若直线l与平面α有两个公共点，则l⊂α，那么B∈α，这与B∉α矛盾，∴l∩α＝A.
11．已知α、β为平面，A、B、M、N为点，a为直线，下列推理错误的是____．(填序号)
①A∈a，A∈β，B∈a，B∈β⇒a⊂β；
②M∈α，M∈β，N∈α，N∈β⇒α∩β＝MN；
③A∈α，A∈β⇒α∩β＝A；
④A、B、M∈α，A、B、M∈β，且A、B、M不共线⇒α、β重合．
【答案】　③
解析　∵A∈α，A∈β，∴A∈α∩β.
由公理可知α∩β为经过A的一条直线而不是点A.
故α∩β＝A的写法错误．
三、解答题
12．已知直线b∥c，且直线a与直线b，c都相交，求证：直线a，b，c共面．
证明　∵b∥c，∴直线b，c可以确定一个平面α.
设a∩b＝A，a∩c＝B，
则A∈a，B∈a，∴A∈α，B∈α，即a⊂α，
故直线a，b，c共面．
13.已知：A∈l，B∈l，C∈l，D∉l，如图所示．求证：直线AD，BD，CD共面．

证明　因为D∉l，所以l与D可以确定平面α，因为A∈l，所以A∈α，又D∈α，所以AD⊂α.同理，BD⊂α，CD⊂α，所以AD，BD，CD在同一平面α内，即它们共面．

B组 能力提升
一、选择题
1．空间中有A，B，C，D，E五个点，已知A，B，C，D在同一个平面内，B，C，D，E在同一个平面内，那么这五个点(　　)
A．共面 B．不一定共面
C．不共面 D．以上都不对
【答案】　B
解析　当B，C，D三点共线时，B，C，D三点不能确定平面．A，B，C，D所在的平面和B，C，D，E所在的平面可能不同，所以A，B，C，D，E五点不一定共面．
2．如图，α∩β＝l，A∈α，C∈β，C∉l，直线AD∩l＝D，过A、B、C三点确定的平面为γ，则平面γ、β的交线必过(　　)

A．点A　　　　　 B．点B
C．点C，但不过点D D．点C和点D
【答案】D　[A、B、C确定的平面γ与直线BD和点C确定的平面重合，故C、D∈γ，且C、D∈β，故C，D在γ和β的交线上．]
3．(多选题)如图，ABCD­A1B1C1D1是长方体，O是B1D1的中点，直线A1C交平面AB1D1于点M，则下列结论正确的是(　　)

A．A，M，O三点共线
B．A，M，O，A1四点共面
C．A，O，C，M四点共面
D．B，B1，O，M四点共面
【答案】ABC　[因为A，M，O三点既在平面AB1D1内，又在平面AA1C内，故A，M，O三点共线，从而易知ABC均正确．]
二、填空题
4．三个互不重合的平面把空间分成n部分，则n所有可能的值为________．
【答案】4,6,7或8　[若三个平面互相平行，则可将空间分为4部分；
若三个平面有两个平行，第三个平面与其他两个平面相交，则可将空间分成6部分；
若三个平面交于一线，则可将空间分成6部分；
若三个平面两两相交且三条交线平行，则可将空间分成7部分；
若三个平面两两相交且三条交线交于一点(如墙角三个墙面的关系)，则可将空间分成8部分．故n的所有可能值为4,6,7或8.]
三、解答题
5.如图所示，在空间四边形ABCD中，E，F分别是AB和CB上的点，G，H分别是CD和AD上的点，且＝＝1，＝＝2.

求证：EH，BD，FG三条直线相交于同一点．
证明　如图，连接EF，GH.因为＝＝1，＝＝2，所以EF∥AC，HG∥AC，且EF≠GH，所以EH，FG共面，且与FG不平行．不妨设EH∩FG＝O，因为O∈EH，EH⊂平面ABD，所以O∈平面ABD，因为O∈FG，FG⊂平面BCD，所以O∈平面BCD.又因为平面ABD∩平面BCD＝BD，所以O∈BD，所以EH，BD，FG三条直线相交于同一点O.


6.如图，已知在四面体A­BCD中，E，F分别是AB，AD的中点，G，H分别是BC，CD上的点，且＝＝2.求证：直线EG，FH，AC相交于同一点．

[证明]　∵E，F分别是AB，AD的中点，
∴EF∥BD，且EF＝BD．
又＝＝2，
∴GH∥BD，且GH＝BD，
∴EF∥GH，且EF>GH，

∴四边形EFHG是梯形，其两腰所在直线必相交．
设两腰EG，FH的延长线相交于一点P，
∵EG⊂平面ABC，FH⊂平面ACD，
∴P∈平面ABC，P∈平面ACD．
又平面ABC∩平面ACD＝AC，
∴P∈AC，故直线EG，FH，AC相交于同一点．
7.已知△ABC在平面α外，其三边所在的直线满足AB∩α＝P，BC∩α＝Q，AC∩α＝R，如图所示，求证：P，Q，R三点共线．

[证明]　法一　∵AB∩α＝P，
∴P∈AB，P∈平面α.
又AB⊂平面ABC，∴P∈平面ABC．
∴由基本事实3可知：点P在平面ABC与平面α的交线上，同理可证Q，R也在平面ABC与平面α的交线上．
∴P，Q，R三点共线．
法二　∵AP∩AR＝A，
∴直线AP与直线AR确定平面APR.
又∵AB∩α＝P，AC∩α＝R，
∴平面APR∩平面α＝PR.
∵B∈平面APR，C∈平面APR，∴BC⊂平面APR.
∵Q∈BC，∴Q∈平面APR，
又Q∈α，∴Q∈PR，
∴P，Q，R三点共线．