2020-2021学年8.6 空间直线、平面的垂直学案设计

这是一份2020-2021学年8.6 空间直线、平面的垂直学案设计，文件包含862直线与平面的垂直的性质2课时解析版docx、862直线与平面的垂直的性质2课时原卷版docx等2份学案配套教学资源，其中学案共28页， 欢迎下载使用。
   8.6.2直线与平面垂直的性质导学案编写：廖云波      初审：谭光垠      终审：谭光垠  廖云波【学习目标】1.记住直线与平面垂直的性质定理，并能应用定理解决有关问题2.会求直线到平面的距离【自主学习】知识点1   直线与平面垂直的性质定理1．文字语言：垂直于同一个平面的两条直线        ．简记为：若线面垂直，则线线平行．2．符号语言：⇒        .3．图形语言：知识点2   直线到平面的距离1．直线与平面平行，则直线上任意一点到平面的距离        ，一条直线与一个平面平行时，这条直线上        这个到平面的距离，叫做这条直线到这个平面的距离．2．如果两个平面平行，那么其中一个平面内的任意一点到另一个平面的距离都相等，我们把它叫做这两个平行平面间的距离．
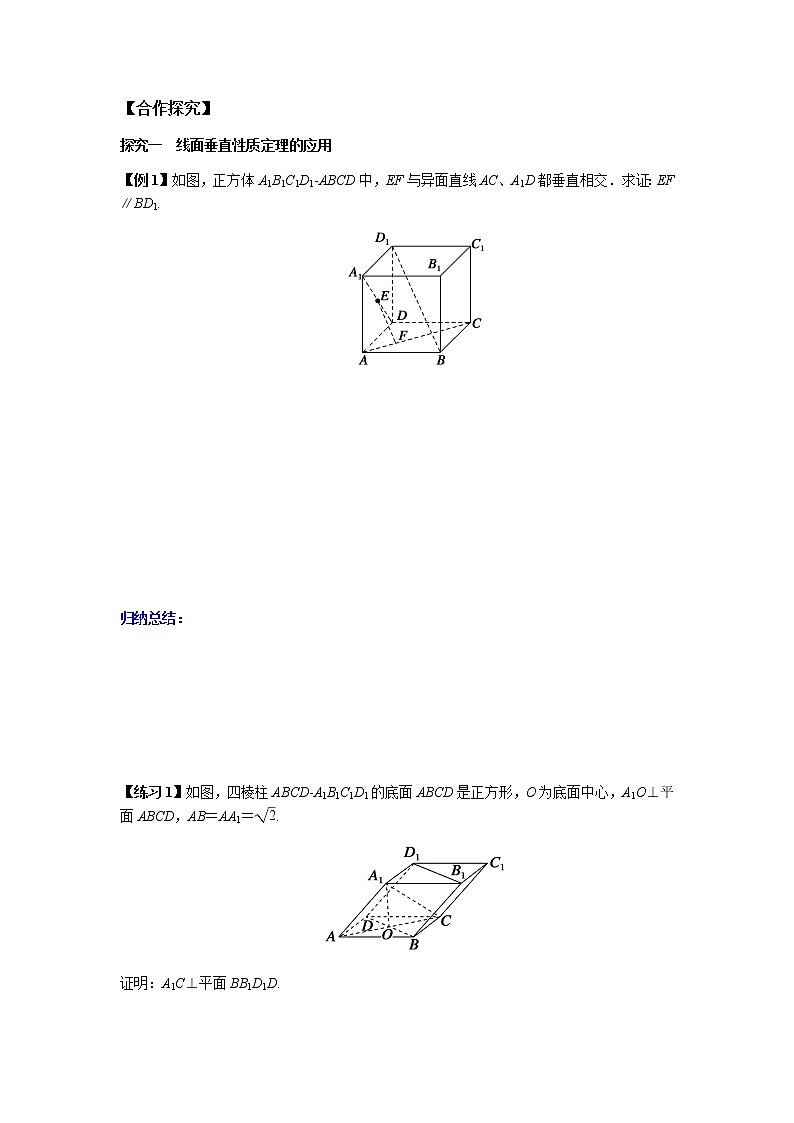
【合作探究】探究一  线面垂直性质定理的应用【例1】如图，正方体A1B1C1D1­ABCD中，EF与异面直线AC、A1D都垂直相交．求证：EF∥BD1.      归纳总结：    【练习1】如图，四棱柱ABCD­A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB＝AA1＝.证明：A1C⊥平面BB1D1D. 
探究二  直线到平面的距离【例2】正方体ABCD­A1B1C1C1，棱长为a，求：(1)直线A1A到平面B1BCC1的距离；(2)直线A1A到平面D1DBB1的距离．         归纳总结：   【练习2】如图，在长方体ABCD­A1B1C1D1中，AB＝2，AD＝1，A1A＝1.(1)证明：直线BC1平行于平面D1AC；(2)求直线BC1到平面D1AC的距离． 
 课后作业A组 基础题一、选择题1．下列命题：①垂直于同一条直线的两个平面互相平行；②垂直于同一个平面的两条直线互相平行；③一条直线在平面内，另一条直线与这个平面垂直，则这两条直线互相垂直．其中正确的个数是(　　)A．0　　　　B．1  C．2　　　　D．3 2．在空间中，下列命题中正确的是(　　)①平行于同一条直线的两条直线互相平行；②垂直于同一条直线的两条直线互相平行；③平行于同一个平面的两条直线互相平行；④垂直于同一个平面的两条直线互相平行．A．①③④   B．①④C．①   D．①②③④ 3．已知平面α与平面β相交，直线m⊥α，则(　　)A．β内必存在直线与m平行，且存在直线与m垂直B．β内不一定存在直线与m平行，不一定存在直线与m垂直C．β内不一定存在直线与m平行，必存在直线与m垂直D．β内必存在直线与m平行，不一定存在直线与m垂直 4．△ABC所在的平面为α，直线l⊥AB，l⊥AC，直线m⊥BC，m⊥AC，则直线l，m的位置关系是(　　)A．相交　　　B．异面  C．平行　　　D．不确定 5.如图，▱ADEF的边AF⊥平面ABCD，且AF＝2，CD＝3，则CE＝(　　)A．2   B．3C.   D. 
6．(多选)如图，直线PA垂直于圆O所在的平面，△ABC内接于圆O，且AB为圆O的直径，点M为线段PB的中点．以下各命题中，真命题为(　　)A．BC⊥PCB．OM∥平面APCC．点B到平面PAC的距离等于线段BC的长D．三棱锥M­PAC的体积等于三棱锥P­ABC体积的一半 二、填空题7．长方体ABCD­A1B1C1D1中，MN在平面BCC1B1内，且MN⊥BC于点M，则MN与AA1的位置关系是      ．  8．直线a和b在正方体ABCD­A1B1C1D1的两个不同平面内，使a∥b成立的条件是        .(只填序号即可)①a和b垂直于正方体的同一个面；②a和b在正方体两个相对的面内，且共面；③a和b平行于同一条棱；④a和b在正方体的两个面内，且与正方体的同一条棱垂直． 9．如图，在正方体ABCD­A1B1C1D1中，M是AB上一点，N是A1C的中点，MN⊥平面A1DC，则MN与AD1的位置关系为      ；若AM＝λAB，则λ＝      . 
三、解答题10．如图，三棱柱ABC­A1B1C1中，侧面BB1C1C为菱形，B1C的中点为O，且AO⊥平面BB1C1C.(1)证明：B1C⊥AB.(2)若AC⊥AB1，∠CBB1＝60°，BC＝1，求三棱柱ABC­A1B1C1的高．           11.如图，在四棱锥P­ABCD中，PD⊥平面ABCD，PD＝DC＝BC＝2，AB＝2DC，AB∥DC，∠BCD＝90°.(1)求证：PC⊥BC；(2)求多面体A­PBC的体积．  
B组 能力提升一、选择题1．在正方体ABCD­A1B1C1D1中，若直线l(与直线BB1不重合)⊥平面A1C1，则(　　)A．B1B⊥l   B．B1B∥lC．B1B与l异面但不垂直   D．B1B与l相交但不垂直 2．已知m，n为异面直线，m⊥平面α，n⊥平面β，直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则(　　)A．α∥β且l∥αB．α⊥β且l⊥βC．α与β相交，且交线垂直于lD．α与β相交，且交线平行于l 二、填空题3．如图所示，在三棱锥P­ABC中，PA⊥平面ABC，D是侧面PBC上的一点，过D作平面ABC的垂线DE，其中D∉PC，则DE与平面PAC的位置关系是       ． 
三、解答题4．如图，在四面体P­ABC中，PA⊥平面ABC，PA＝AB＝1，BC＝，AC＝2.(1)证明：BC⊥平面PAB.(2)在线段PC上是否存在点D，使得AC⊥BD，若存在，求PD的值，若不存在，请说明理由．