人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积同步训练题

这是一份人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积同步训练题，文件包含831棱柱棱锥棱台的表面积和体积基础练-2020-2021学年下学期高一数学同步课堂人教A版2019必修第二册解析版doc、831棱柱棱锥棱台的表面积和体积基础练-2020-2021学年下学期高一数学同步课堂人教A版2019必修第二册原卷版doc等2份试卷配套教学资源，其中试卷共12页， 欢迎下载使用。
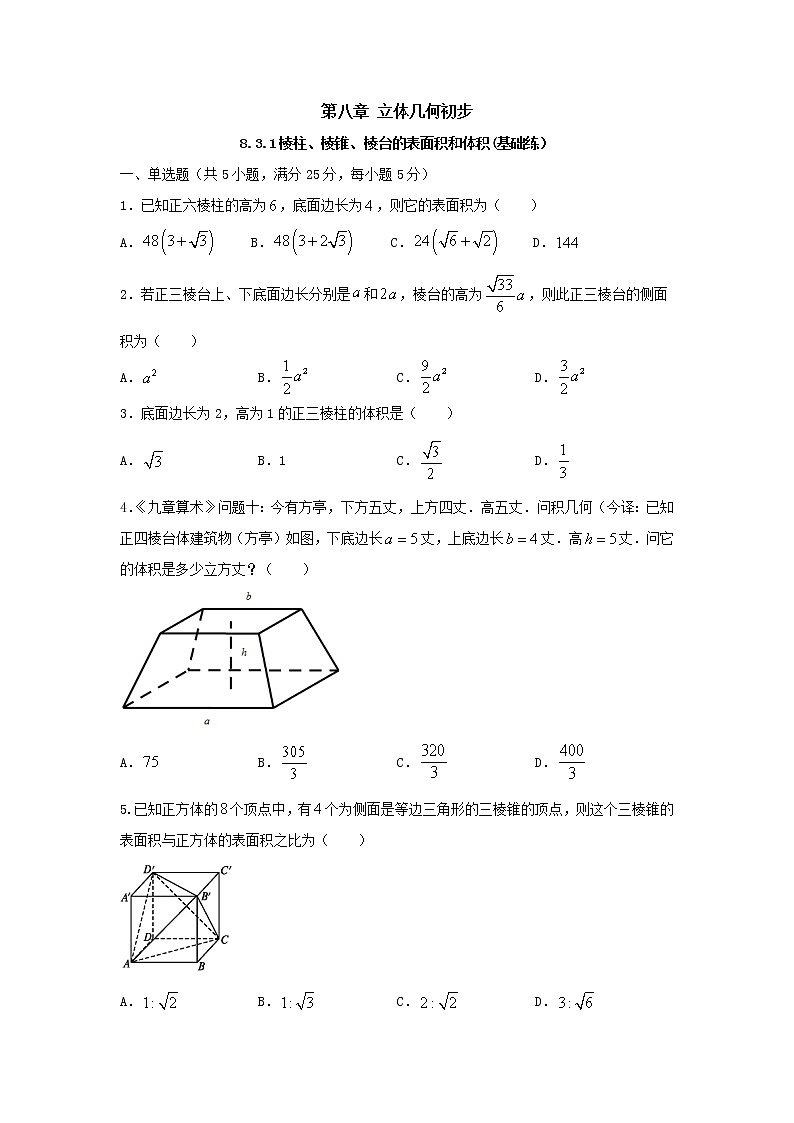
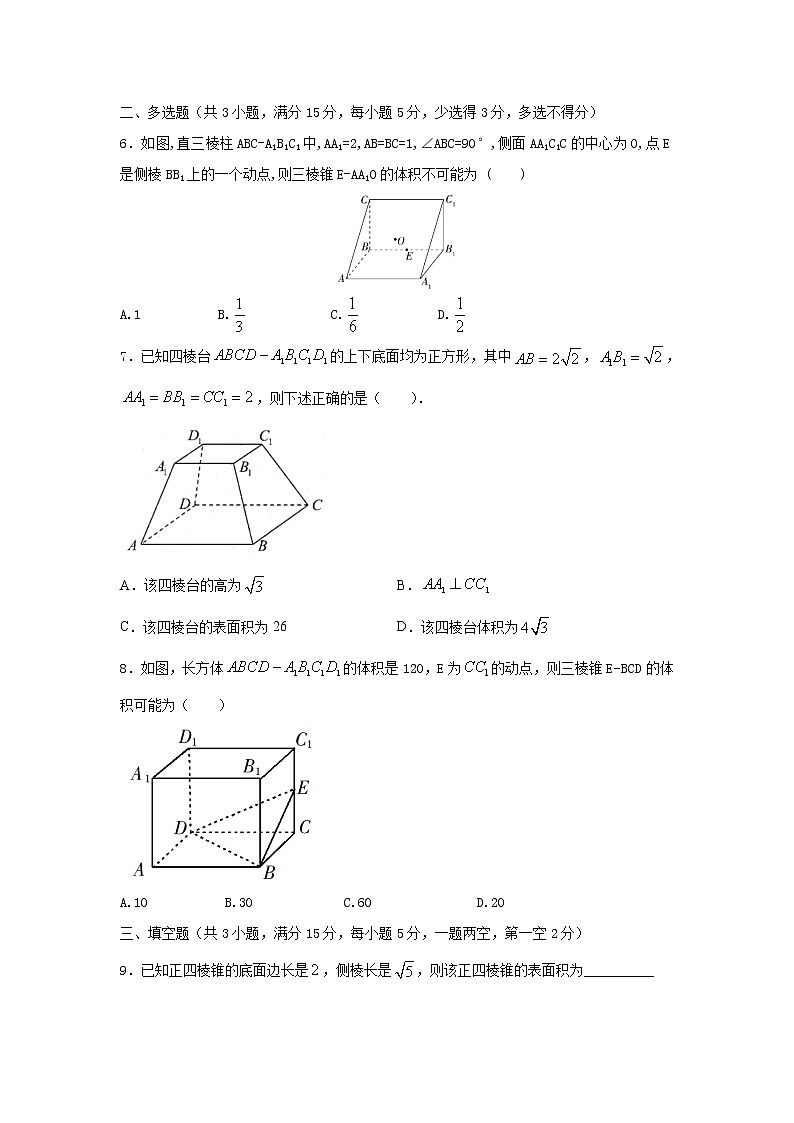
第八章 立体几何初步8.3.1棱柱、棱锥、棱台的表面积和体积(基础练）一、单选题（共5小题，满分25分，每小题5分）1．已知正六棱柱的高为，底面边长为，则它的表面积为（    ）A．     B．     C．    D．【答案】A【解析】由题知侧面积为，两底面积之和为，所以表面积.故选：A.2．若正三棱台上、下底面边长分别是和，棱台的高为，则此正三棱台的侧面积为（    ）A． B． C． D．【答案】C【解析】如图，分别为上、下底面的中心，分别是，的中点，过作于点E.在直角梯形中，，，.在中，，则..     故选：C3．底面边长为2，高为1的正三棱柱的体积是（    ）A． B．1 C． D．【答案】A【解析】底面边长为2，高为1的正三棱柱的体积是故选：A4．《九章算术》问题十：今有方亭，下方五丈，上方四丈．高五丈．问积几何（今译：已知正四棱台体建筑物（方亭）如图，下底边长丈，上底边长丈．高丈．问它的体积是多少立方丈？（    ） A． B． C． D．【答案】B【解析】. 故选:B5.已知正方体的个顶点中，有个为侧面是等边三角形的三棱锥的顶点，则这个三棱锥的表面积与正方体的表面积之比为（    ）A． B． C． D．【答案】B【解析】如图所示，在正方体中，三棱锥符合题目条件，且三棱锥的四个侧面全为等边三角形，设正方体的棱长为，则三棱锥的棱长为，所以正方体的表面积为，，即三棱锥的表面积为，则三棱锥的表面积与正方体的表面积之比为：．故选：B．二、多选题（共3小题，满分15分，每小题5分，少选得3分，多选不得分）6．如图,直三棱柱ABC-A1B1C1中,AA1=2,AB=BC=1,∠ABC=90°,侧面AA1C1C的中心为O,点E是侧棱BB1上的一个动点,则三棱锥E-AA1O的体积不可能为 (　　)A.1           B.            C.           D.【答案】ABD　【解析】∵点E是侧棱BB1上的一个动点,∴以平面AA1O为底面的三棱锥E-AA1O的高为定值,又=××2=,∴=××=,故C正确;故选:ABD7．已知四棱台的上下底面均为正方形，其中，，，则下述正确的是（    ）．A．该四棱台的高为 B．C．该四棱台的表面积为26 D．该四棱台体积为【答案】AD【解析】由棱台性质，画出切割前的四棱锥，由于，，可知△ 与相似比为；则，，则，则，该四棱台的高为，对；因为，则与夹角为，不垂直，错；该四棱台的表面积为，错；8．如图，长方体的体积是120，E为的动点，则三棱锥E−BCD的体积可能为（    ）A.10           B.30             C.60               D.20   【答案】AD【解析】因为长方体的体积为120，所以，因为为的动点，所以，()由长方体的性质知底面，所以是三棱锥的底面上的高，所以三棱锥的体积.20,故选:AD三、填空题（共3小题，满分15分，每小题5分，一题两空，第一空2分）9．已知正四棱锥的底面边长是，侧棱长是，则该正四棱锥的表面积为__________【答案】【解析】如图所示，在正四棱锥中，取中点，连接，则为直角三角形，所以，所以表面积.故答案为：12.10．某组合体如图所示，上半部分是正四棱锥，下半部分是长方体.正四棱锥的高为，，，则正四棱锥的斜高为__________,该组合体的表面积为_____________【答案】2   20【解析】由题意，正四棱锥的斜高为，该组合体的表面积为.故答案为：2   20四、解答题：（本题共3小题，共45分。解答应写出文字说明、证明过程或演算步骤。）12．如图，正三棱锥的底面边长为2，侧棱长为3.
 （1）求正三棱锥的表面积；（2）求正三棱锥的体积.【答案】（1）；（2）.【解析】（1）取的中点D，连接，在中，可得.∴.∵正三棱锥的三个侧面是全等的等腰三角形，∴正三棱锥的侧面积是.∵正三棱锥的底面是边长为2的正三角形，∴.则正三棱锥的表面积为；（2）连接，设O为正三角形的中心，则底面.且.在中，.∴正三棱锥的体积为.13．已知长方体的体积为，则求三棱锥的体积.【答案】【解析】设长方体的底面积为，高为，则长方体的体积为，由题意可知，三棱锥的底面积为，高为，因此，三棱锥的体积为，14．14．如图是一个以A1B1C1为底面的直三棱柱被一平面所截得到的几何体，截面为ABC，已知A1B1＝B1C1＝2，∠A1B1C1＝90°，AA1＝4，BB1＝3，CC1＝2， 求：（1）该几何体的体积．（2）截面ABC的面积．【答案】(1)6;(2)【解析】（1）以同样大的几何体，进行补形，可得一直三棱柱，其底面为△A1B1C1，高为4+2＝6，∴所求几何体的体积为V2×2×6＝6；（2）△ABC中，AB，BC，AC2，∴△ABC为等腰三角形，底边AC的高为：h；∴截面ABC的面积为S△ABC2．