高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用教学ppt课件

这是一份高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用教学ppt课件，共16页。PPT课件主要包含了假设C为最大角则，C90°，C30°，C105°，所以C无解，证明方法，正弦定理等内容，欢迎下载使用。

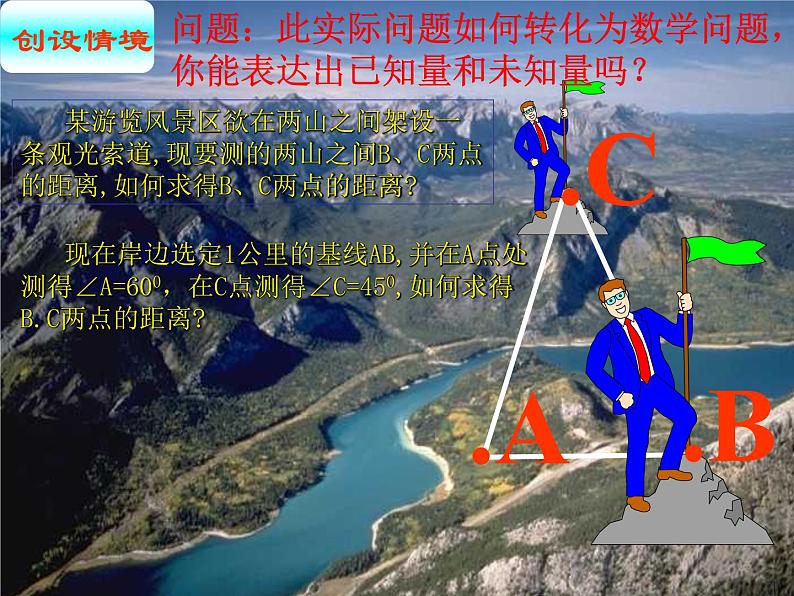
某游览风景区欲在两山之间架设一条观光索道,现要测的两山之间B、C两点的距离,如何求得B、C两点的距离?
现在岸边选定1公里的基线AB,并在A点处测得∠A=600，在C点测得∠C=450,如何求得B.C两点的距离?
问题：此实际问题如何转化为数学问题，你能表达出已知量和未知量吗？
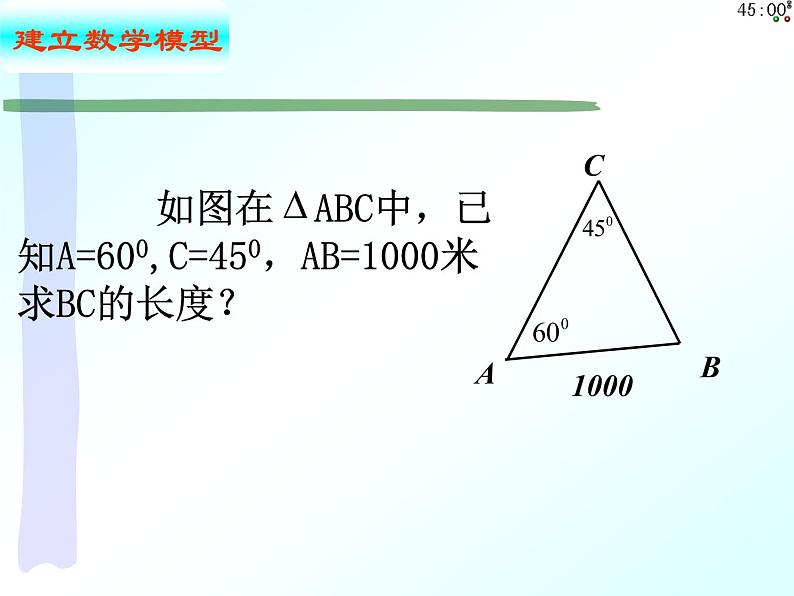
如图在 ABC中，已知A=600,C=450，AB=1000米 求BC的长度？
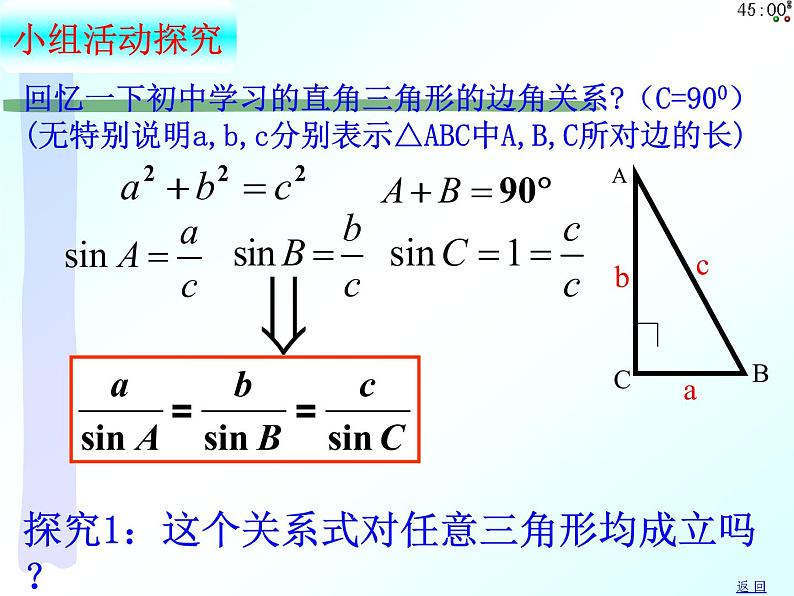
回忆一下初中学习的直角三角形的边角关系?（C=900） (无特别说明a,b,c分别表示△ABC中A,B,C所对边的长)
探究1：这个关系式对任意三角形均成立吗？
探究2：如何证明 这个等式？
证法一：不妨设C为最大角，
当C为直角时，等式成立；
当C为锐角时，过A点作AD垂直BC交于D点
当C为钝角时，过A点作AD垂直于BC交BC的延长线于点D
探究3：能不能利用我们刚学过的知识解决
过A作AD垂直于BC于D,如图,于是
其中,当C为锐角或直角时,
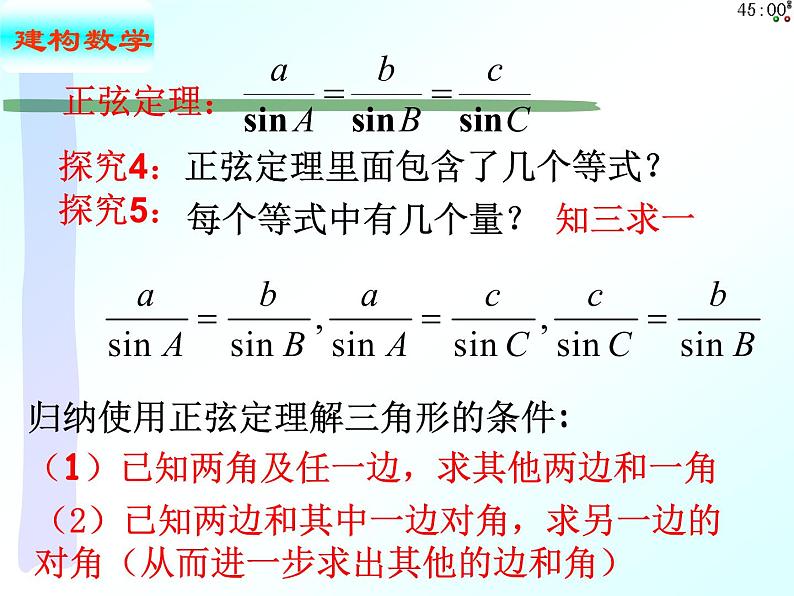
探究4：正弦定理里面包含了几个等式？
归纳使用正弦定理解三角形的条件:
（1）已知两角及任一边，求其他两边和一角
（2）已知两边和其中一边对角，求另一边的对角（从而进一步求出其他的边和角）
已知两角和任一边求其他两边和一角
本题已知条件和问题分别是什么？

答案：A=600，b= ;c=
在△ABC中，已知a=8， b= ， A=30°，求角B，C和边c
已知两边和其中一边所对的角,求其他边和角
在△ABC中，已知a=16，b= ， B=45° .求角A，C和边c
法二：利用三角形中大边对大角，小边对小角
已知两边和其中一边所对的角,求其他边和角可用正弦定理解决
②作高法证明正弦定理.
①已知两角及任一边，求其他两边和一角
②已知两边和其中一边所对的角，求另一边所对的角
（从而进一步求出其他的边和角）
已知三角形两边和其中一边所对的角时，三角形的解的个数如何判别？