第八章 立体几何初步（客观题题型全覆盖）- 学年高一数学下学期期末备考专题全攻略（人教A版2019）学案

这是一份第八章 立体几何初步（客观题题型全覆盖）- 学年高一数学下学期期末备考专题全攻略（人教A版2019）学案，文件包含第八章立体几何初步客观题题型全覆盖解析版doc、第八章立体几何初步客观题题型全覆盖原卷版doc等2份学案配套教学资源，其中学案共58页， 欢迎下载使用。
第八章 立体几何初步
客观题题型全覆盖

类型
对应典例
空间几何体的结构特征
典例一
空间中直线、平面的位置关系
典例二
异面直线的夹角
典例三
线面角
典例四
二面角
典例五
点到平面的距离
典例六
与球有关的问题
典例七
典例一、空间几何体的结构特征
1．如图，边长为1的正方形是一个水平放置的平面图形的直观图，则平面图形以为轴旋转一周所围成的几何体的体积为（ ）

A． B． C． D．
【答案】C
【详解】
由题意可得，，，
由直观图画出原平面图形如下：

因此，将以为轴旋转一周所围成的几何体是以为底面圆半径，以为高的圆锥；将以为轴旋转一周所围成的几何体是以为底面圆半径，以为高的圆柱挖去一个同底等高的圆锥；
因此将平面图形以为轴旋转一周所围成的几何体的体积为.
故选：C.
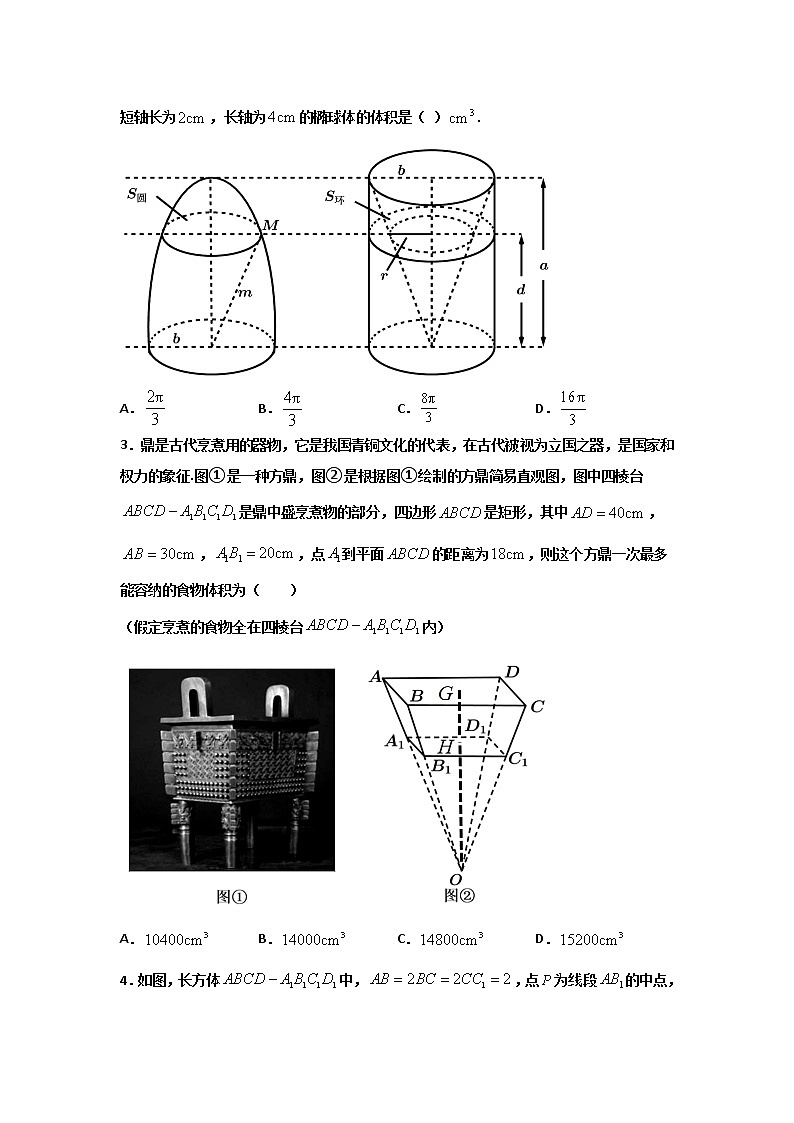
2．祖暅(公元5-6世纪，祖冲之之子，是我国齐梁时代的数学家).他提出了一条原理：“幂势既同，则积不容异.”这句话的意思是：两个等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等.该原理在西方直到十七世纪才由意大利数学家卡瓦列利发现，比祖暅晚一千一百多年.椭球体是椭圆绕其轴旋转所成的旋转体如图将底面直径皆为，高皆为的椭半球体及已被挖去了圆锥体的圆柱体放置于同一平面上，用平行于平面的平面于距平面任意高处截得到及两截面，可以证明总成立据此，短轴长为，长轴为的椭球体的体积是（ ）.

A． B． C． D．
【答案】C
【详解】根据题意，因为总成立，
所以半椭球体的体积为，
由题意可知，，，
所以半椭球体的体积为，
从而椭球体的体积是.
故选：C.
3．鼎是古代烹煮用的器物，它是我国青铜文化的代表，在古代被视为立国之器，是国家和权力的象征.图①是一种方鼎，图②是根据图①绘制的方鼎简易直观图，图中四棱台是鼎中盛烹煮物的部分，四边形是矩形，其中，，，点到平面的距离为，则这个方鼎一次最多能容纳的食物体积为（ ）
（假定烹煮的食物全在四棱台内）

A． B． C． D．
【答案】D
【详解】几何体为四棱台，所以延长必交于一点，记为O，
且四棱锥相似于，所以.过点作OH⊥面于H，
作OG⊥面于G，则,又，解得：OG=,OH=，
四棱台的体积.
故选：D
4．如图，长方体中，，点为线段的中点，，，分别为线段和棱上任意一点，则的最小值为（ ）

A． B．5 C． D．2
【答案】B
【详解】取中点，过作面，如图：

则，故，
而对固定的点，当时，最小.
此时由面，可知，
∴，,
故.
故选：B.
5．2020年12月4日，中国科学技术大学宣布该校潘建伟教授等人成功构建76个光子的量子计算原型机“九章”（命名为“九章”是为了纪念中国古代最早的数学专著《九章算术》），求解数学算法高斯玻色取样只需200秒，而目前世界最快的超级计算机要用6亿年，这一突破使我国成为全球第二个实现“量子优越性”的国家．《九章算术》是我国古代的数学巨著，其卷第五“商功”有如下的问题：“今有刍甍，下广三丈，袤四丈，上衰二丈，无广，高一丈．问积几何？”意思为：“今有底面为矩形的屋脊形状的多面体（如图）”，下底面宽丈，长丈，上棱丈，与平面平行．与平面的距离为1丈，则它的体积是（ ）

A．4立方丈 B．5立方丈 C．6立方丈 D．8立方丈
【答案】B
【详解】如图，过点作平面，垂足为，过点作平面，垂足为，
过作，交于，交于，过作，交于，交于，
所以，，且四边形与四边形都是矩形；
所以它的体积



（立方丈）
故选：B


（多选）6．在中，角，，所对的边分别为，，，且，将分别绕边，，所在的直线旋转一周，形成的几何体的体积分别记为，，，侧面积分别记为，，，则（ ）
A． B．
C． D．
【答案】ABC
【详解】
将绕边所在的直线旋转一周形成的几何体是圆锥，其底面半径是，母线长为，高为. 所以其体积，其侧面积；

将绕边所在的直线旋转一周形成的几何体是圆锥，其底面半径是，母线长为，高为. 所以其体积，其侧面积；

将绕边所在的直线旋转一周形成的几何体是两个底面重合的圆锥，其底面半径是，母线长分别为和，高之和为. 所以其体积，其侧面积.

对于选项A，

故A正确；
对于选项B，
，
故B正确；
对于选项C：
，故C正确；
对于选项D：
，而，
所以，故D错误.
故选：ABC.

典例二、空间中直线、平面的位置关系
1．已知空间中两平面，直线，则“”是“”的（ ）
A．充分而不必要条件
B．必要而不充分条件
C．充要条件
D．既不充分也不必要条件
【答案】A
【详解】且，知：；而且，则与平面的关系可能有、、，
∴“”是“”的充分不必要条件.
故选：A
2．如图，在正方体中，、分别为、的中点，则下列直线中与直线相交的是（ ）

A．直线 B．直线 C．直线 D．直线
【答案】D
【详解】通过图像易知：
直线、直线、直线与直线不在同一平面内，
直线与在同一平面内且不平行，
故直线与相交，
故选：D.
3．设，，为不重合的平面，，为不重合的直线，则其中正确命题的序号为（ ）
①，，则
②，，，则
③，，，则
④，，，则
A．①③ B．②③ C．②④ D．③④
【答案】D
【详解】①中，，可以相交并垂直于，①错误
②中，直线可能不在平面内，②错误
③中，垂直于互相垂直的两条直线的两个平面垂直，故③正确；
④中，两个平面垂直于第三个平面，这两个平面的交线也垂直于第三个平面，故④正确，
故选：D
4．已知m，n是两条不同的直线，α，β是两个不同的平面，则下列判断正确的是（ ）
A．若α⊥β，mα，nβ，则直线m与n一定平行
B．若m⊥α，n⊥β，α⊥β，则直线m与n可能相交､平行或异面
C．若m⊥α，nα，则直线m与n一定垂直
D．若mα，nβ，αβ，则直线m与n一定平行
【答案】C
【详解】

如图示，在正方体中
对于A：若α⊥β，mα，nβ，不妨取面ABCD为平面α，面ABA1B1为平面β，若取m为BC，n为A1B1，则直线m与n异面，故A错误；
对于B：若m⊥α，n⊥β，α⊥β，不妨取面ABCD为平面α，面ABA1B1为平面β，则直线m与n垂直，不可能平行，故B错误；
对于C：若m⊥α，nα，因为nα，过n作平面，则ln.因为m⊥α，所以m⊥l，又ln，所以m⊥n.故C正确；
对于D：若mα，nβ，αβ，不妨取面ABCD为平面α，面A1B1C1D1为平面β，则两个平面内的直线m与n可能平行，也可能异面.故D错误.
故选：C.
5．三棱柱中，点在上，且，若平面，则（ ）
A． B． C． D．
【答案】A
【详解】如图，连接，交于，连接，
平面，平面，平面平面，
，中，为中点，为中点，
，.
故选：A.

6．在棱长为2的正方体中，为的中点.当点在平面内运动时，有平面，则线段的最小值为（ ）
A．1 B． C． D．
【答案】B
【详解】取CD中点P，中点Q，连接PQ、PN、QN，如图所示：

因为P、N分别为CD、BC中点，
所以，
同理，P、Q分别为CD、中点，
所以，
又，平面PQN，，平面，
所以平面平面，
因为平面，
所以平面，又点在平面内运动，
所以点M在平面和平面的交线上，即，
在中，，，，
所以，
所以，

所以N点到PQ的最小距离.
所以线段的最小值为.
故选：B
7．已知棱长为1的正方体，是的中点，动点在正方体内部或表面上，且平面，则动点的轨迹所形成区域的面积是（ ）
A． B． C． D．
【答案】A
【详解】

如图所示 E、F、G、M分别是、、、的中点，
则，，所以平面，平面，且，
所以平面 平面，故点P的轨迹为矩形.
，所以，所以.
故选：A
8．如图，是正方体棱的中点，是棱上的动点，下列命题中：①若过的平面与直线垂直，则为的中点；②存在使得；③存在使得的主视图和侧视图的面积相等；④四面体的体积为定值.其中正确的是（ ）

A．①②④ B．①③
C．③④ D．①③④
【答案】D
【详解】
①当为的中点，将平移至，则为的四等分点，即，过点作，设=4，则=4，=5，，

所以
所以在△中，，故
所以，
所以过的平面与直线垂直
②过作，易知为的中点，此时和相交，所以和异面，故②错误；
③当为时，的主视图和侧视图的面积相等，故③成立；
④因为,故面，故上任一点到平面距离相等，且的面积固定，故为定值的，故④正确；
故选：D.
8．如图，在正方体，中，是棱的中点，是线段（不含端点）上的一个动点，那么在点的运动过程中，下列说法中正确的有（ ）

A．存在某一位置，使得直线和直线相交
B．存在某一位置，使得平面
C．点与点到平面的距离总相等
D．三棱锥的体积不变
【答案】BCD
【详解】
对于A，假设存在，则四点共面，而点不在平面内，故A错误．
对于B，因为，所以平面，所以当是直线与平面的交点时就满足要求，故B正确．
对于C，因为的中点在平面内，所以点与点到平面的距离总相等，故C正确．
对于D，连接，交于O，则O为中点，
所以，又平面，平面，
所以平面，所以点到平面的距离为定值，
从而三棱锥的体积为定值，即三棱锥的体积为定值，故D正确．

故选：BCD
10．如图，矩形中，已知为的中点．将沿着向上翻折至得到四棱锥．平面与平面所成锐二面角为，直线与平面所成角为，则下列说法错误的是（ ）

A．若为中点，则无论翻折到哪个位置都有平面平面
B．若为中点，则无论翻折到哪个位置都有平面
C．
D．存在某一翻折位置，使
【答案】C
【详解】
若为中点，连接交于点，则面，又面，所以平面平面，故A正确；
取中点，则，，又，
所以四边形PECQ是平行四边形，又平面，平面，所以平面，故B正确；
过作平面，则在上，所以平面与平面所成锐二面角为（或其补角），
，故C错误；
若，又，则，故D正确，
故选：C．



典例三、异面直线的夹角
1．如图，为圆锥底面直径，点是底面圆上异于的动点，已知，圆锥侧面展开图是圆心角为的扇形，当与所成角为时，与所成角为（ ）

A． B． C． D．
【答案】C
【详解】

设圆锥母线长为，则，解得，
，与所成角，
， 中，
作与圆交于点，
连接，四边形为平行四边形，，
连接，则为与所成角，
中，可得，
，
故选：C.
2．在正方体中，，，分别为，，的中点，则异面直线与所成角的余弦值为（ ）


A． B． C． D．
【答案】B
【详解】
连接，在正方体中，
由，分别为，的中点，则
所以，所以（或其补角）为异面直线与所成角
设正方体的棱长为2，则,

所以在中，
故选：B


3．已知直四棱柱中，底面为正方形，若直四棱柱的所有顶点都在半径为2的球面上，则当该直四棱柱的侧面积最大时，异面直线与所成角的余弦值为（ ）
A． B． C． D．
【答案】D
【详解】
连接BD，由题易知为直四棱柱外按球的直径，设，，
则，所以，
则该直四棱柱的侧面积为，
当且仅当，时取等号，连接，交于，易知，所以为异面直线与所成的角.因为，，所以，所以，所以异面直线与所成角的余弦值为.
故选：D．

4．在长方体中，，，，过点作直线与直线及直线所成角均为70°，这样的直线的条数为（ ）
A．4 B．3 C．2 D．1
【答案】A
【详解】
，，
则
，
而，，
所以，，
所以直线和直线所成的角为，
设与直线平行的直线为，与直线平行的直线为，
将直线、直线和直线平移至点，
则当三条直线在同一平面时，这样的直线不存在；
若三条直线不在同一平面，,是的角平分线，在PD的上方有一条直线PE与所成的角为70°，同理也满足题意.所以这样的直线有四条．
故这样的直线条数为4．
故选：A

5．已知长方体中，，，是上任意一点(不是端点)，是的中点，则异面直线与所成角的正切值的最小值为（ ）
A． B． C． D．
【答案】D
【详解】
如图所示，取中点，连接，，

∵是中点，且为正方形，
∴∥∥
则与所成角即为与所成角，设角度为
又∵AB⊥平面
∴⊥平面
又∵平面,
∴
∴
∵==3为定值，
∴要使最小，则最小，
当最小时,需⊥
∵∠=∠
∴△∽△
∴
又∵
∴
此时
∴异面直线与所成角的正切值的最小值为.
故选：D.
6．如图，在正方体中，，分别是，的中点，为线段上的动点(不含端点)，则下列结论中正确的是（ ）

A．平面
B．存在点使得
C．存在点使得异面直线与所成的角为60°
D．三棱锥的体积为定值
【答案】ABD
【详解】
如图，易证，平面，则有平面，故A正确；

设中点为，若为中点，则有，，，
则平面，则，
因为，所以，故B正确；
设正方体棱长为2，取中点为，连接，
因为，所以异面直线与所成的角即为，
在直角三角形中，，即，故C错误；
易知点到平面的距离为定值，则三棱锥的体积为定值，故D正确.
故选：ABD
7．在正方体中，M是棱的中点，P是底面ABCD内(包括边界)的一个动点，若平面，则异面直线MP与所成角的取值范围是（ ）
A． B． C． D．
【答案】C
【详解】如图，以不轴建立空间直角坐标系，设，
则，，取中点，中点，连接，则，，
，，
所以，同理，
又平面，平面，所以平面，
同理平面，而，平面，
所以平面平面，
P是底面ABCD内(包括边界)的一个动点，若平面，则在线段上．
因为，所以与所成的角，就是与所成的锐角或直角．
是等边三角形，与所平角最大为（为中点时），最小为（与或重合时），
所以所求角的范围是．
故选：C．



典例四、线面角
1．已知正方体的体积为，点在面上，且，到的距离分别为2，，则直线与平面所成角的正弦值为（ ）
A． B． C． D．
【答案】B.
【详解】
如图所示:

设正方体的边长为，则，故，即，
∴，连接，，
∴，则点在上且为中点，连接与交于，连接，
可知平面，则为直线与平面所成角，
在直角三角形中，∴.
故选：B.
2．许多球状病毒的空间结构可抽象为正二十面体．正二十面体的每一个面均为等边三角形，共有12个顶点、30条棱．如图所示，由正二十面体的一个顶点和与相邻的五个顶点可构成正五棱锥，则与面所成角的余弦值约为（ ）（参考数据）

A． B． C． D．
【答案】A
【详解】
由题意，在面上的射影，如下图示，

∴五个三角形都是等腰三角形且，易知，而，令，
∴，又正二十面体的每一个面均为等边三角形即，且面，
∴与面所成角的余弦值为.
故选：A
3．如图，在大小为的锐二面角中，，，、，，，、分别为、的中点.记直线与半平面的夹角为，直线与半平面的夹角为.若，则（ ）

A．， B．，
C．， D．，
【答案】A
【详解】
如下图所示，构造直三棱柱，分别取、的中点、，连接、、，

则，，则，同理可得，
且，、分别为、的中点，所以，且，
所以，四边形为平行四边形，所以，，同理可知，
所以，，，故，
且，、分别为、的中点，且，
设，则，，，
，则为的中点，故点与点重合，
，，，平面，
平面，则，故，
在中，，则，
，则，所以，，
由于、均为锐角，所以，，则，
过点在平面内作，垂足为点，连接，
平面，平面，，
又，，，所以，，
且为锐角，所以，，
，，
所以，，
易知、，且余弦函数在上单调递减，所以，.
故选：A.
4．如图，在正方体中，是中点，点在线段上，若直线与平面所成的角为，则的取值范围是（ ）．

A． B． C． D．
【答案】A
【详解】
如图，设正方体棱长为1，，则，

以为原点，分别以，，所在直线为，，轴建立空间直角坐标系．
则，故，，又，则，所以．
在正方体中，可知体对角线平面，
所以是平面的一个法向量，
所以．
所以当时，取得最大值，当或1时，取得最小值．
所以.
故选：A．
典例五、二面角
1．如图，已知，分别是正方体的棱，的中点，设为二面角的平面角，则（ ）

A． B．
C． D．
【答案】C
【详解】
如图，设正方体的棱长为，
在平面内过点作于点，连接，
则即是二面角的平面角，
且，由
解得，∴，∴，

故选:：C.
2．已知菱形，，将△沿折起，使二面角的大小为，则三棱锥的体积为（ ）
A． B． C． D．
【答案】A
【详解】
由题意可得如下示意图，E为BD中点，∠AEC=60°，

∵是菱形，，
∴，即△AEC为等边三角形，则A到CE的高为，
又，，，有面，面，
∴面面，且面面，故为三棱锥的高，
∵，
∴.
故选：A.
3．如图，将矩形纸片折起一角落得到，记二面角的大小为，直线，与平面所成角分别为，，则（ ）．

A． B．
C． D．
【答案】A
【详解】

如图，过作平面，垂足为，过作，垂足为，
设，
因为平面，平面，故，
而，故平面，而平面，
所以，故，
又，.
在直角三角形中，，同理，
故，同理，
故，故，
整理得到，
故，
整理得到即，
若，由 可得即，
但，故，即，矛盾，
故.
故A正确，B错误.
由可得，
而均为锐角，故，，故CD错误.
故选：A.
（多选）4．已知正方体中，以下结论正确的有（ ）

A．点P在直线BC1上运动时，三棱锥A-D1PC的体积不变
B．点P在直线BC1上运动时，直线AP与平面AD1C所成角的大小不变
C．点P在直线BC1上运动时，二面角P-AD1-C的大小不变
D．M是平面上到点D和C1距离相等的点，则点M的轨迹是过点D1的直线
【答案】ACD
【详解】
因为，，且平面，平面，所以平面，所以上的点到平面的距离相等，所以三棱锥的体积不变，故A正确；由图可知，当点在直线上运动时，直线与平面所成角和直线与平面所成角不相等，故B错误；因为平面，所以二面角的大小等于平面与平面所成角的大小，所以二面角的大小不变，故C正确；因为是平面上到点和距离相等的点，所以点的轨迹是平面与线段的垂直平分线所在平面的交线，即点的轨迹是平面与平面的交线，所以点的轨迹是过点的直线，故D正确；
故选：ACD.
5．如图，矩形中，已知，，为的中点． 将沿着向上翻折至，记锐二面角的平面角为，与平面所成的角为，则下列结论不可能成立的是（ ）

A． B．
C． D．
【答案】D
【详解】
记中点为，连接，连接与交于点， 依题意知四边形是正方形.

，故锐二面角的平面角为，
平面，过作于，则，
而相交于平面内，
故平面，故连接，则与平面所成的角为.
记，因为中，，
中，，所以①，选项A成立；
将①平方得：，所以，，
易见，都是锐角，则，∴，而，
根据余弦函数的单调性可知，，选项C成立；
因为，，若使，则需，
即当，可以成立，即B可能成立；
另外，由，都是锐角，且知，，知.
由选项C知，∴，选项D错误．
故选：D.

典例六、点到平面的距离
1．已知圆柱中，点，，为底面圆周上的三点，为圆柱的母线，，，则点到平面的距离为（ ）
A． B．1 C． D．
【答案】A
【详解】
如图所示，由题意知：平面，平面，
∴平面平面，又面面，
∴过点作，则平面，即为点到平面的距离，
在△中，，故，
故选：A

2．圆台如图所示，为圆的一条直径， 为圆弧上靠近点的一个三等分点，若，，则点到平面的距离为（ ）

A． B． C． D．
【答案】D
【详解】
如图，连接、、、，易知底面，

因为，，所以，，
因为为圆弧上靠近点的一个三等分点，所以，，
因为为圆的一条直径，所以，，，
因为底面，所以三棱锥的体积，
因为是圆的圆心，、、都在圆上，所以，
因为，，，所以，
设点到平面的距离为，
由等体积法易知，解得，
故选：D.

典例七、与球有关的问题
1．在矩形中，，沿对角线进行翻折，则三棱锥外接球的表面积为（ ）
A． B． C． D．
【答案】D
【详解】
因为在翻折过程中，始终不变，
所以的中点到，，，四点的距离始终相等，三棱锥外接球的直径为，
所以外接球的表面积为，
故选：D
2．正三棱锥P－ABC底面边长为2，M为AB的中点，且PM⊥PC，则三棱锥P－ABC外接球的体积为（ ）
A． B． C． D．
【答案】C
【详解】

由图，设，则，而，
因为PM⊥PC，所以由勾股定理得即解得，
由对称性可知：三棱锥P－ABC外接球的球心在三棱锥P－ABC的高PD上，
假设为O点，则，因为,
所以，
又由于点D是三角形ABC的外心，且三角形ABC为等边三角形，
所以,
在三角形ODC中，由勾股定理得,
即，
解得，
所以三棱锥P－ABC外接球的体积为.
故选：C
3．已知正方体的外接球的体积为，若分别为棱的中点，则三棱锥内切球的半径为（ ）
A． B． C． D．
【答案】B
【详解】

设正方体外接球的半径为，由正方体的外接球的体积为得：.
设正方体的棱长为，则，解得：；
由题意得：，，，，
，，，.
又，，平面，平面，
三棱锥的表面积；
设三棱锥内切球的半径为，
根据等体积法得：，
即.
故选：B.
4．在棱长为的正方体中，球同时与以为公共顶点的三个面相切，球同时与以为公共顶点的三个面相切，且两球相切于点，若球，的半径分别为，，则（ ）
A．
B．
C．这两个球的体积之和的最小值是
D．这两个球的表面积之和的最小值是
【答案】C
【详解】
球同时与以为公共顶点的三个面相切，以为对角线可构造一个正方体，边长为
所以同理

则
所以
故这两个球的体积之和为：
因为，所以
即，当且仅当 时等号成立;
这两个球的表面积之和
当且仅当时等号成立
故A,B,D项均错误.
故选：C.
5．在棱长为的正方体中，为棱上一点，且到的距离与到的距离相等，则四面体的外接球的表面积为（ ）
A． B． C． D．
【答案】B
【详解】
连接交于点，连接、、、，如下图所示，

在正方体中，四边形为正方形，且，则为的中点，
因为，所以.
设，则，易知，，
，由已知可得，可得，解得，
将三棱锥补成长方体，
设三棱锥的外接球半径为，则，则，
因此，三棱锥的外接球的表面积为.
故选：B.
6．学生到工厂参加劳动实践，用薄铁皮制作一个圆柱体，圆柱体的全面积为，则该圆柱体的外接球的表面积的最小值是（ ）
A． B． C． D．
【答案】B
【详解】
设圆柱的高为，底面圆的半径为，该圆柱外接球的半径为，
由题意可得，则；所以，，则，
根据圆柱与球的对称性可得：，
所以该圆柱体的外接球的表面积为，当且仅当，即时，等号成立.
故选：B.
7．在三棱锥中，平面平面，，则三棱锥的外接球的表面积为（ ）
A． B． C． D．
【答案】C
【详解】
如图，取中点，中点，连接，是等边三角形，则
因为平面平面，平面平面，平面，所以平面，又平面，所以，
过作平面，则，
因为，所以三棱锥的外接球的球心在上，设球心为，连接，设外接球半径为，
由已知，，，，
在直角梯形中，，，，
所以球表面积为．
故选：C．