专题19 立体几何综合小题-2022年新高考数学高频考点 题型专项练习(新高考适用)

这是一份专题19 立体几何综合小题-2022年新高考数学高频考点 题型专项练习(新高考适用)，文件包含专题19立体几何综合小题解析版docx、专题19立体几何综合小题原卷版docx等2份试卷配套教学资源，其中试卷共160页， 欢迎下载使用。
专题19 立体几何综合小题必刷100题
(初级)1-30题
一、单选题
1．已知正四棱锥的底面边长和侧棱长均为2，则该正四棱锥的体积为（ ）
A． B． C． D．

2．已知，为两条不同的直线，，为两个不同的平面，则下列说法正确的是（ ）
A．若，，则 B．若，，则
C．若，，，则 D．若，，则

3．如图，空间四边形中，点在线段上，且，为的中点，，则，，的值分别为（ ）

A．，， B．，， C．，， D．，，

4．已知，，是三个不同的平面，，是两条不同的直线，下列命题为真命题的是（ ）
A．若，，则 B．若，，则
C．若，，则 D．若，，则

5．已知四棱锥的正视图和侧视图均为边长为2（单位：cm）的正三角形，俯视图为正方形，则该四棱锥的体积（单位：）是（ ）
A． B． C． D．

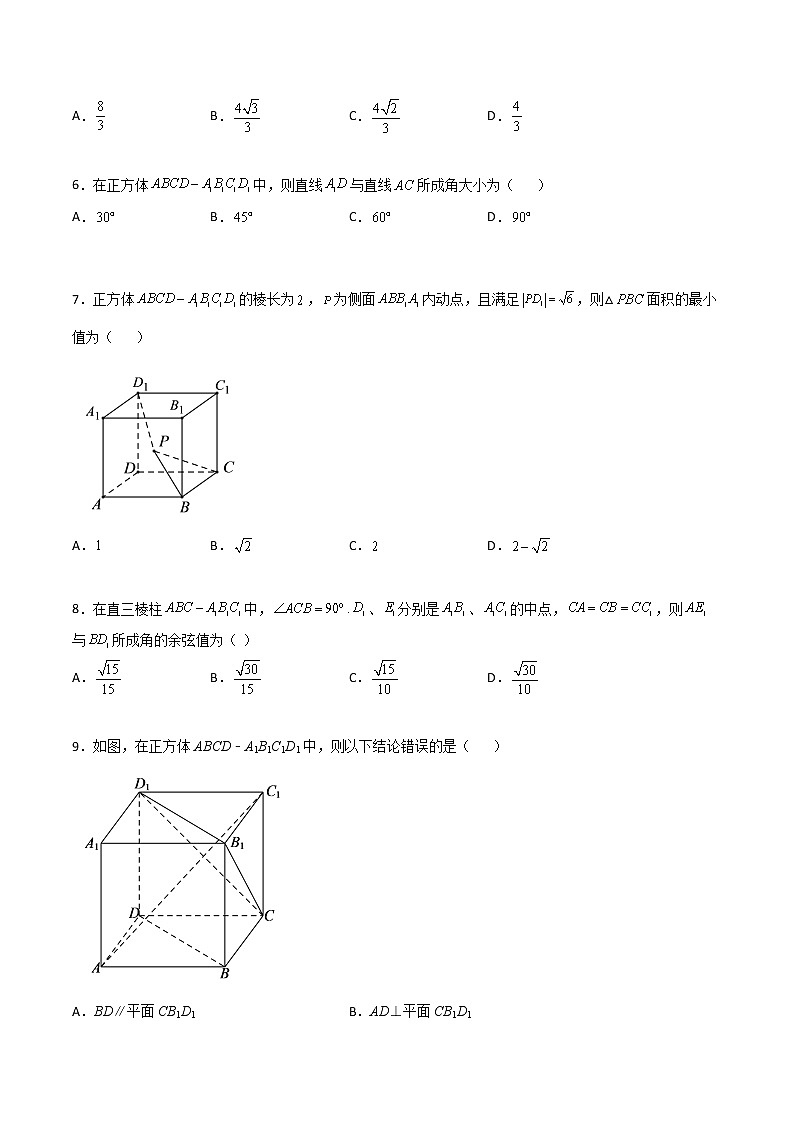
6．在正方体中，则直线与直线所成角大小为（ ）
A． B． C． D．

7．正方体的棱长为，为侧面内动点，且满足，则△面积的最小值为（ ）

A． B． C． D．

8．在直三棱柱中，.、分别是、的中点，，则与所成角的余弦值为（ ）
A． B． C． D．

9．如图，在正方体ABCD﹣A1B1C1D1中，则以下结论错误的是（ ）

A．BD∥平面CB1D1 B．AD⊥平面CB1D1
C．AC1⊥BD D．异面直线AD与CB1所成的角为45°

10．已知向量＝(2m＋1，3，m－1)，＝(2，m，－m)，且，则实数m的值等于（ ）
A． B．－2
C．0 D．或－2

11．正方体ABCD­-A1B1C1D1中，E，F分别是线段BC，CD1的中点，则直线A1B与直线EF的位置关系是（ ）
A．相交 B．异面
C．平行 D．垂直

12．已知直三棱柱中，，，，则异面直线与所成角的余弦值为（　　）
A． B．0 C． D．

13．把一个皮球放入如图所示的由8根长均为20 cm的铁丝接成的四棱锥形骨架内，使皮球的表面与8根铁丝都有接触点（皮球不变形），则皮球的半径为（ ）

A． cm B．10 cm
C． cm D．30 cm

14．一种特殊的四面体叫做“鳖臑”，它的四个面均为直角三角形.如图，在四面体PABC中，设E，F分别是PB，PC上的点，连接AE，AF，EF（此外不再增加任何连线），则图中直角三角形最多有（ ）

A．6个 B．8个
C．10个 D．12个

15．在四棱锥中，底面是边长为的正方形，且，则四棱锥外接球的表面积为（ ）
A． B． C． D．

二、多选题
16．给出下列命题，其中正确的有（ ）
A．空间任意三个向量都可以作为一组基底
B．已知向量，则、与任何向量都不能构成空间的一组基底
C．已知空间向量，，则
D．已知空间向量，，则向量在向量上的投影向量的坐标是

17．如图，正方体的棱长为4，以下结论正确的是（ ）

A．直线与是异面直线
B．直线与平行
C．直线与垂直
D．三棱锥的体积为

18．如图，正方体的棱长为1，点是棱上的一个动点（包含端点），则下列说法正确的是（ ）

A．存在点，使面
B．二面角的平面角大小为
C．的最小值是
D．到平面的距离最大值是

19．已知、是两条不同的直线，、、是三个不同的平面.下列说法中正确的是（ ）
A．若，，，则 B．若，，则
C．若，，，则 D．若，，，则

20．在下列条件中，不能使M与A，B，C一定共面的是（ ）
A．＝2－－； B．；
C．； D．＋＋＋＝0；

21．如图，在正方体中，O为底面的中心，P为所在棱的中点，M，N为正方体的顶点．则满足的是（ ）
A． B．
C． D．

22．设一空心球是在一个大球(称为外球)的内部挖去一个有相同球心的小球(称为内球)，已知内球面上的点与外球面上的点的最短距离为1，若某正方体的所有顶点均在外球面上､所有面均与内球相切，则（ ）
A．该正方体的核长为2 B．该正方体的体对角线长为
C．空心球的内球半径为 D．空心球的外球表面积为

23．在正三棱柱中，，，与交于点，点是线段上的动点，则下列结论正确的是（ ）
A．
B．存在点，使得
C．三棱锥的体积为
D．直线与平面所成角的余弦值为

第II卷（非选择题）

三、填空题
24．已知正方体ABCD-A1B1C1D1的棱长为2，M、N分别为BB1、BC的中点，则三棱锥N-DMC1的体积为___________.

25．已知正三棱锥的底面边长是，侧棱与底面所成角为，则此三棱锥的体积为__．

26．如图，在直三棱柱中，∠ACB＝90°，，则异面直线与AC所成角的余弦值是__________________．


27．已知圆台上底半径为1，下底半径为3，高为2，则此圆台的外接球的表面积为______．

28．如图，已知平行六面体中，底面是边长为2的正方形，侧棱长为3，且，则__.


29．如图，在空间四边形OABC中，，点M在OA上，且，N为BC的中点，则用向量表示向量________．


30．已知四棱锥P﹣ABCD的顶点都在球O的球面上，底面ABCD是边长为2的正方形，且PA⊥平面ABCD.若四棱锥P﹣ABCD的体积为，则球O的表面积为___________.




















(中级)1-40题
一、单选题
1．在三棱锥P－ABC中，，△PAB，△PAC，△PBC的面积分别记为，且，则此三棱锥的内切球的半径为（ ）
A． B．
C． D．

2．在立体几何探究课上，老师给每个小组分发了一个正四面体的实物模型，同学们在探究的过程中得到了一些有趣的结论.已知直线平面，直线平面，F是棱BC上一动点，现有下列三个结论：

①若分别为棱的中点，则直线平面；
②在棱BC上存在点F，使平面；
③当F为棱BC的中点时，平面平面.
其中所有正确结论的编号是（ ）
A．③ B．①③ C．①② D．②③

3．已知圆台上底面半径为3，下底面半径为4，高为7，若点A、B、C在下底面圆的圆周上，且，点Р在上底面圆的圆周上，则的最小值为（ ）
A．246 B．226 C．208 D．198

4．北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性，规定：多面体顶点的曲率等于与多面体在该点的面角之和的差（多面体的面的内角叫做多面体的面角，角度用弧度制），多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和，例如：正四面体在每个顶点有3个面角，每个面角是，所以正四面体在各顶点的曲率为，故其总曲率为，则四棱锥的总曲率为（ ）

A． B． C． D．

5．如图，正方体的棱长为1，线段上有两个动点E，F，且，则三棱锥的体积为（ ）

A． B． C． D．不确定

6．如图已知正方体，点是对角线上的一点且，，则（ ）

A．当时，平面 B．当时，平面
C．当为直角三角形时， D．当的面积最小时，

7．如图所示，已知空间四边形的每条边和对角线长都等于a，点E、F、G分别为AB、AD、DC的中点，则a2等于（　　）

A．2• B．2• C．2• D．2•

8．如图一，矩形中，，交对角线于点，交于点．现将沿翻折至的位置，如图二，点为棱的中点，则下列判断一定成立的是（ ）

A． B．平面
C．平面 D．平面平面

9．点M是棱长为3的正方体中棱的中点，，动点P在正方形（包括边界）内运动，且平面，则的长度范围为（ ）
A． B． C． D．

10．如图，在正方体中，点M在线段(不包含端点)上运动，则下列判断中正确的是（ ）

①平面； ②异面直线与所成角的取值范围是；
③平面恒成立； ④三棱锥的体积不是定值．
A．①③ B．①② C．①②③ D．②④

11．在四面体中，平面，，，，则该四面体的外接球的表面积是（ ）
A． B．100π C． D．20π

12．已知圆锥的母线长为，侧面展开图的圆心角为，则该圆锥外接球的表面积为（ ）
A． B． C． D．

13．如图，四棱锥的底面为矩形，底面，，，点是的中点，过，，三点的平面与平面的交线为，则下列结论中正确的有（ ）

（1）平面；
（2）平面；
（3）直线与所成角的余弦值为；
（4）平面截四棱锥所得的上、下两部分几何体的体积之比为．
A．1个 B．2个
C．3个 D．4个

14．在四棱锥中，平面平面，且是边长为2的正三角形，是正方形，则四棱锥外接球的表面积为（ ）

A． B． C． D．

15．已知在正四面体ABCD中，E是AD的中点，P是棱AC上的一动点，BP＋PE的最小值为，则该四面体内切球的体积为（ ）
A．π B．π
C．4π D．π

16．在棱长为2的正方体中，点，，，分别为棱，，，的中点，若平面平面，且平面与棱，，分别交于点，，，其中点是棱的中点，则三棱锥的体积为（ ）
A．1 B． C． D．

17．已知球，过其球面上，，三点作截面，若点到该截面的距离是球半径的一半，且，，则球的表面积为（ ）（注：球的表面积公式
A． B． C． D．

18．如图，在正三棱柱ABC-A1B1C1中，AC=CC1，P是A1C1的中点，则异面直线BC与AP所成角的余弦值为（ ）

A．0 B． C． D．

19．一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱，这个四棱锥的底面为正方形，且底面边长与各侧棱长相等，这个三棱锥的底面边长与各侧棱长也都相等．设四棱锥、三棱锥、三棱柱的高分别为、、，则（ ）
A． B． C． D．

20．如图，二面角的大小是，线段．，与所成的角为．直线与平面所成的角的正弦值是（ ）

A． B． C． D．

二、多选题
21．如图，已知正方体，则四个推断正确的是（ ）

A． B．
C．平面平面 D．平面平面

22．正方体的棱长为2，E，F，G分别为的中点，则（ ）

A．直线与直线垂直 B．直线与平面平行
C．平面截正方体所得的截面面积为 D．点C到平面的距离为

23．正四棱锥的所有棱长为2，用垂直于侧棱的平面截该四棱锥，则（ ）
A．截面可以是三角形
B．与底面所成的角为
C．与底面所成的角为
D．当平面经过侧棱中点时，截面分四棱锥得到的上下两部分几何体体积之比为3：1

24．如图，等腰直角三角形的斜边为正四面体的侧棱，，直角边绕斜边旋转一周，在旋转的过程中，下列说法正确的是（ ）

A．三棱锥体积的最大值为
B．三棱锥体积的最小值为
C．存在某个位置，使得
D．设二面角的平面角为，且，则

25．如图，在平行六面体中，以顶点A为端点的三条棱长均为6，且它们彼此的夹角都是60°，下列说法中不正确的是（ ）

A．
B．平面
C．向量与的夹角是60°
D．直线与AC所成角的余弦值为

26．正方体中，是棱的中点，在侧面上运动，且满足平面.以下命题正确的有（ ）

A．侧面上存在点，使得
B．直线与直线所成角可能为
C．平面与平面所成锐二面角的正切值为
D．设正方体棱长为1，则过点，，的平面截正方体所得的截面面积最大为

27．如图，边长为1的正方形ABCD所在平面与正方形ABEF所在平面互相垂直，动点M，N分别在正方形对角线AC和BF上移动，且.则下列结论中正确的有（ ）

A．当时，ME与CN相交
B．MN始终与平面BCE平行
C．异面直线AC与BF所成的角为
D．当时，MN的长最小，最小为

28．(多选)如图，ABCD­A1B1C1D1为正方体，下面结论正确的是（ ）

A．BD∥平面CB1D1
B．AC1⊥BD
C．AC1⊥平面CB1D1
D．异面直线AD与CB1所成的角为60°

29．已知四边形ABCD为正方形，GD⊥平面ABCD，四边形DGEA与四边形DGFC也都为正方形，连接EF，FB，BE，H为BF的中点，则下列结论正确的是（ ）
A．DE⊥BF
B．EF与CH所成角为
C．EC⊥平面DBF
D．BF与平面ACFE所成角为

30．下图中正方体边长为2，则下列说法正确的是（ ）

A．平面平面
B．正方体外接球与正四面体外接球半径相等均为
C．正四面体内切球半径为
D．四面体内切球半径为

第II卷（非选择题）

三、填空题
31．空间四面体中，，，，直线和所成的角为，则该四面体的外接球的表面积为 __.

32．如图，A、B、C、D、P是球O上5个点，ABCD为正方形，球心O在平面ABCD内，，，则PA与CD所成角的余弦值为______．


33．已知圆锥、圆柱的底面半径和体积都相等，则它们的轴截面的面积之比的比值是___________

34．中国有悠久的金石文化，印信是金石文化的代表之一.下左图是南北朝官员独孤信的印信，它是由正方形和正三角形围成.右图是根据这只印信作出的直观图，直观图的所有顶点都在一正方体的表面上（如果一个正八边形的八个顶点都在这个正方体同一个侧面的四条棱上，那么这个八边形的边长就等于这个直观图的棱长）.若这个正方体的所有顶点都在半径为的球面上，则这只印信的表面积为__________.


35．如图，在直三棱柱中，，，已知G与E分别为和的中点，D和F分别为线段AC和AB上的动点（不包括端点），若，则线段DF的长度的平方取值范围为__________.


36．如图，在长方体中，已知，点，分别在棱，上.二面角的大小为30°.若三棱锥的体积为，则三棱锥的外接球的表面积为___________.



37．异面直线a、b所成角为，直线c与a、b垂直且分别交于A、B，点C、D分别在直线a、b上，若，，，则________．

38．已知四棱锥S﹣ABCD的底面是边长为4的正方形，SD⊥面ABCD，点M、N分别是AD、CD的中点，P为SD上一点，且SD＝3PD＝3，H为正方形ABCD内一点，若SH∥面PMN，则SH的最小值为__．

39．如图，在中，，，是棱的中点，以为折痕把折叠，使点到达点的位置，则当三棱锥体积最大时，其外接球的表面积为___________.


40．在如图所示的实验装置中，正方形框架的边长都是，且平面平面，活动弹子分别在正方形对角线上移动，若，则长度的最小值为__________．


















(高级)1-30题
一、单选题
1．已知四面体ABCD的所有棱长均为，M，N分别为棱AD，BC的中点，F为棱AB上异于A，B的动点．有下列结论：
①线段MN的长度为1；
②若点G为线段MN上的动点，则无论点F与G如何运动，直线FG与直线CD都是异面直线；
③的余弦值的取值范围为；
④周长的最小值为．
其中正确结论的为（ ）
A．①② B．②③ C．③④ D．①④

2．已知三棱锥，其中平面，，，.已知点为棱（不含端点）上的动点，若光线从点出发，依次经过平面与平面反射后重新回到点，则光线经过路径长度的取值范围为（ ）
A． B．
C． D．

3．如图，已知锐二面角的大小为，，，，，，，C，D为AB，MN的中点，若，记AN，CD与半平面所成角分别为，，则（ ）


A．， B．，
C．， D．，

4．在棱长为2的正方体中，点是对角线上的点（点与不重合），有以下四个结论：

①存在点，使得平面平面；
②存在点，使得平面；
③若的周长为L，则L的最小值为；
④若的面积为，则．
则正确的结论为（ ）
A．①③ B．①②③ C．①②④ D．②④

5．在棱长为1的正方体中，点P是正方体棱上一点，若满足的点P的个数为4，则d的取值范围为（ ）
A． B． C． D．

6．在三棱锥中，，点在面上的投影是的垂心，二面角的平面角记为，二面角的平面角记为，二面角的平面角记为，则（ ）

A． B．
C． D．

7．已知正方体的棱长为1，是的中点，是棱上一点（不包括端点），则下列结论错误的是（ ）
A．三棱锥的体积为定值
B．存在点，使得直线与直线相交
C．当是棱的中点时，直线与直线所成的角为
D．平面截正方体所得的截面是五边形

8．如图，在等边三角形中，分别是线段上异于端点的动点，且，现将三角形沿直线折起，使平面平面，当从滑动到的过程中，则下列选项中错误的是（ ）

A．的大小不会发生变化 B．二面角的平面角的大小不会发生变化
C．与平面所成的角变大 D．与所成的角先变小后变大

9．蹴鞠，又名“蹴球”“蹴圆”等，“蹴”有用脚蹴、踢的含义，“鞠”最早系外包皮革、内饰米糠的球，因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动，类似今日的踢足球活动.如图所示，已知某“鞠”的表面上有四个点，，，满足，，则该“鞠”的表面积为（ ）

A． B．
C． D．

10．已知在中，斜边，，若将沿斜边上的中线折起，使平面平面，则三棱锥的外接球的表面积为（ ）
A． B． C． D．

11．如图，在长方体中，，，，点是的中点，点为棱上的动点，则平面与平面所成的锐二面角正切的最小值是（ ）

A． B．
C． D．

12．已知正方体的棱长为，M，N为体对角线的三等分点，动点P在三角形内，且三角形的面积，则点P的轨迹长度为（ ）

A． B． C． D．

13．已知半球与圆台有公共的底面，圆台上底面圆周在半球面上，半球的半径为1，则圆台侧面积取最大值时，圆台母线与底面所成角的余弦值为（ ）
A． B． C． D．

14．如图，等腰直角中，，点为平面外一动点，满足，，给出下列四个结论：

①存在点，使得平面平面；
②存在点，使得平面平面；
③设的面积为，则的取值范围是；
④设二面角的大小为，则的取值范围是.
其中正确结论是（ ）
A．①③ B．①④ C．②③ D．②④

15．已知AB、CD是圆O的两条直径，且，如图1，沿AB折起，使两个半圆面所在的平面垂直，折到点位置，如图2．设直线与直线OC所成的角为，则（ ）

A．且 B．且
C．且 D．且

二、多选题
16．如图，底面ABCD为边长是4的正方形，半圆面底面ABCD．点P为半圆弧(不含A，D点)一动点．下列说法正确的是（ ）

A．三梭锥P—ABD的每个侧面三角形都是直角三角形
B．三棱锥P—ABD体积的最大值为
C．三棱锥P—ABD外接球的表面积为定值
D．直线PB与平面ABCD所成最大角的正弦值为

17．已知正方体的棱长为2，动点在正方形内，则（ ）
A．若，则三棱锥的的外接球表面积为
B．若平面，则不可能垂直
C．若平面，则点的位置唯一
D．若点为中点，则三棱锥的体积是三棱锥体积的一半

18．为弘扬中华民族优秀传统文化，某学校组织了《诵经典，获新知》的演讲比赛，本次比赛的冠军奖杯由一个铜球和一个托盘组成，如图①，已知球的体积为，托盘由边长为的正三角形铜片沿各边中点的连线垂直向上折叠而成，如图②.则下列结论正确（ ）

A．经过三个顶点的球的截面圆的面积为
B．异面直线与所成的角的余弦值为
C．多面体的体积为
D．球离球托底面的最小距离为

19．已知边长为的菱形中，，将沿翻折，下列说法正确的是（ ）
A．在翻折的过程中，直线，始终不可能垂直
B．在翻折的过程中，三棱锥体积最大值为
C．在翻折过程中，三棱锥表面积最大时，其内切球表面积为
D．在翻折的过程中，点在面上的投影为，为棱上的一个动点，的最小值为

20．如图，是由具有公共直角边的两块直角三角板组成的三角形，，.现将沿斜边翻折成△不在平面内）.若，分别为和的中点，则在翻折过程中，下列结论正确的是（ ）

A．平面
B．与不可能垂直
C．二面角正切值的最大值为
D．直线与所成角的取值范围为

21．已知边长为的菱形中，，将沿翻折，下列说法正确的是（ ）
A．在翻折的过程中，直线，可能相互垂直
B．在翻折的过程中，三棱锥体积最大值为
C．在翻折的过程中，三棱锥表面积最大时，其内切球表面积为
D．在翻折的过程中，点在面上的投影为，为棱上的一个动点，的最小值为

22．已知正方体的棱长为2，是底面的中心，是棱上一点（不与端点重合），则（ ）
A．平面截正方体所得截面一定是梯形
B．存在点，使得三棱锥的体积为
C．存在点，使得与相交
D．当是棱的中点时，平面截正方体外接球所得截面圆的面积

23．在四面体中，，，直线，所成的角为60°，，，则四面体的外接球表面积为（ ）
A． B． C． D．

第II卷（非选择题）

三、填空题
24．已知一正三棱锥的体积为，设其侧面与底面所成锐二面角为，则当等于______时，侧面积最小．

25．球面几何学是几何学的一个重要分支，在航海、航空、卫星定位等面都有广泛的应用，如图，A，B，C是球面上不同的大圆（大圆是过球心的平面与球面的交线）上的三点，经过这三个点中任意两点的大圆的劣弧分别为，由这三条劣弧围成的图形称为球面．已知地球半径为R，北极为点N，P，Q是地球表面上的两点若P，Q在赤道上，且，则球面的面积为________；若，则球面的面积为________．


26．如图，在矩形中，是边的中点，将沿直线折成，使得二面角的平面角为锐角，点在线段上运动(包括端点)，当直线与平面所成角最大时，在底面内的射影面积为___________.


27．已知三棱锥的三条侧棱两两垂直，与底面成角，是平面内任意一点，则的最小值是________.

28．已知正方体的棱长为2，点E是棱的中点，点在平面内，若，，则的最小值为_________．



29．在棱长为的正方体中，过对角线的一个平面交于，交于，得四边形，给出下列结论：
①四边形有可能为梯形；
②四边形有可能为菱形；
③四边形在底面内的投影一定是正方形；
④四边形有可能垂直于平面；
⑤四边形面积的最小值为.
其中正确结论的序号是_____________

30．在棱长为4的正方体中，E，F分别是和的中点，经过点A，E，F的平面把正方体截成两部分，则截面的周长为________.