



所属成套资源:2022年新高考数学高频考点 题型专项练习(新高考适用)
专题20 立体几何综合大题-2022年新高考数学高频考点 题型专项练习(新高考适用)
展开
这是一份专题20 立体几何综合大题-2022年新高考数学高频考点 题型专项练习(新高考适用),文件包含专题20立体几何综合大题解析版docx、专题20立体几何综合大题原卷版docx等2份试卷配套教学资源,其中试卷共252页, 欢迎下载使用。
专题20 立体几何综合大题必刷100题
(初级)1-30题
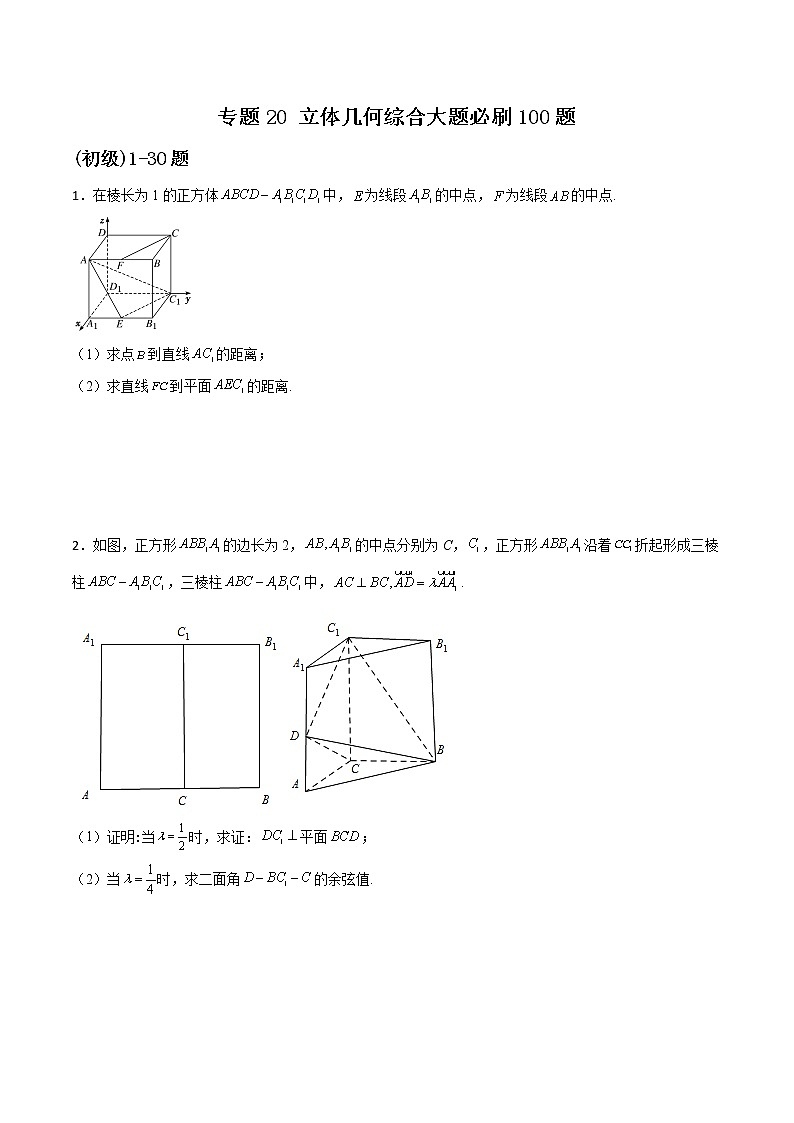
1.在棱长为1的正方体中,为线段的中点,为线段的中点.
(1)求点到直线的距离;
(2)求直线到平面的距离.
【答案】(1);(2).
【分析】
(1)以为原点,所在直线分别为轴,轴,轴,建立空间直角坐标系,取,,根据空间向量点到直线距离公式,可得点点到直线的距离;
(2)易证平面,则点到平面的距离为直线到平面的距离,求出平面的一个法向量,再求出,根据点到面的距离公式,可得直线到平面的距离.
【详解】
以为原点,所在直线分别为轴,轴,轴,建立如图所示的空间直角坐标系,
则,
所以,,, .
(1)取,,则.
所以,点到直线的距离为.
(2)因为,所以,所以平面.
所以点到平面的距离为直线到平面的距离.
设平面的法向量为,则
所以
所以
取,则.所以,是平面的一个法向量.
又因为,所以点到平面的距离为.
即直线到平面的距离为.
2.如图,正方形的边长为2,的中点分别为C,,正方形沿着折起形成三棱柱,三棱柱中,.
(1)证明:当时,求证:平面;
(2)当时,求二面角的余弦值.
【答案】(1)详见解析;(2)
【分析】
(1)要证明线面垂直,转化为证明线线垂直,关键证明,;
(2)以点为原点,建立空间直角坐标系,分别求平面和平面的法向量,利用法向量公式求二面角的余弦值.
【详解】
(1)当时,点是的中点,
因为,所以,又,
所以,所以,
因为,,所以平面,平面
所以,且,
所以平面;
(2)因为,,两两互相垂直,所以以点为原点,以,,作为轴的正方向,建立空间直角坐标系,如下图,
平面,所以向量是平面的法向量,
,,,,,
设平面的法向量,
所以,即 ,令,, ,
所以平面的一个法向量,
,
所以二面角的余弦值是
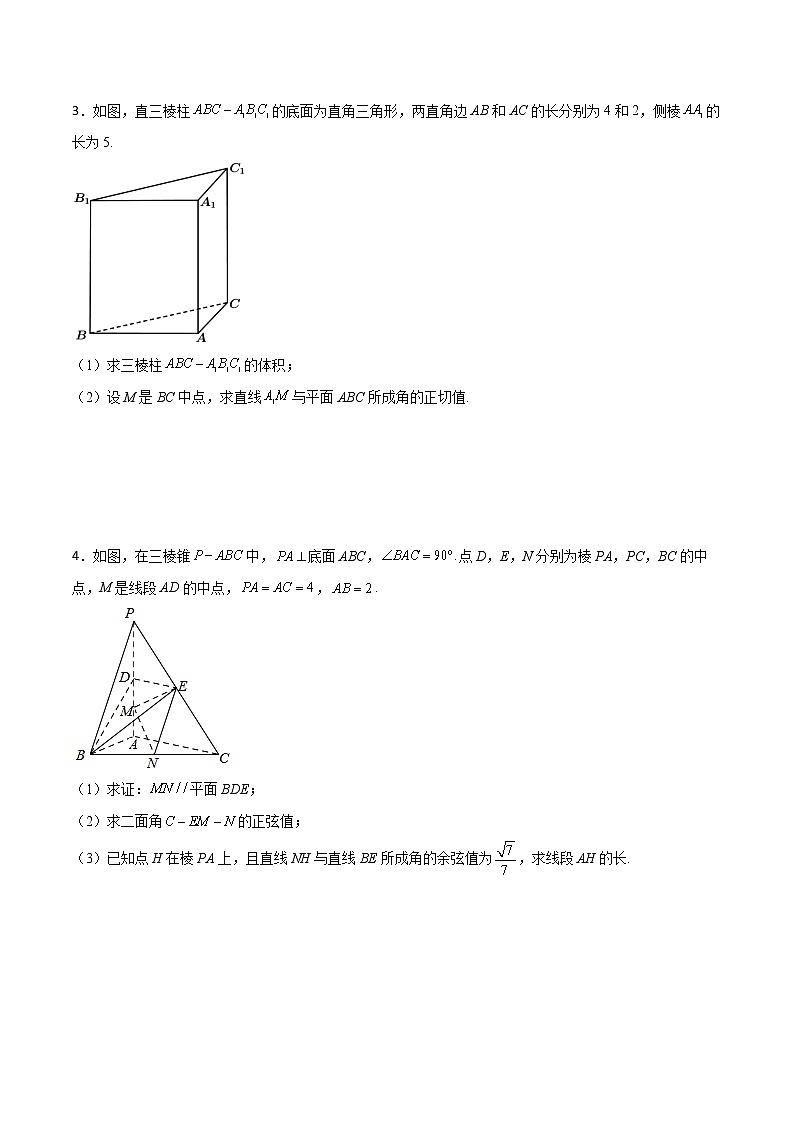
3.如图,直三棱柱的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱的长为5.
(1)求三棱柱的体积;
(2)设M是BC中点,求直线与平面ABC所成角的正切值.
【答案】(1)20;(2).
【分析】
(1)根据棱柱的体积公式进行求解即可;
(2)根据线面角的定义,结合锐角三角函数定义进行求解即可.
【详解】
(1)直三棱柱的底面为直角三角形,
两直角边AB和AC的长分别为4和2,侧棱的长为5.
三棱柱的体积:
.
(2)连接AM,
直三棱柱的底面为直角三角形,
两直角边AB和AC的长分别为4和2,侧棱的长为5,M是BC中点,
底面ABC,,
是直线与平面ABC所成角,
,
直线与平面ABC所成角的正切值为.
4.如图,在三棱锥中,底面ABC,点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,,.
(1)求证:平面BDE;
(2)求二面角的正弦值;
(3)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为,求线段AH的长.
【答案】(1)证明见解析;(2);(3)4
【分析】
(1)根据三角形中位线定理,结合面面平行的判定定理和性质进行证明即可;
(2)建立空间直角坐标系,利用空间向量夹角公式进行求解即可;
(3)利用空间向量夹角公式进行求解即可.
【详解】
(1)证明:取AB中点F,连接MF、NF,
为AD中点,
,
平面BDE,平面BDE,
平面BDE.
为BC中点,
,
又D、E分别为AP、PC的中点,
,则.
平面BDE,平面BDE,
平面BDE.
又,平面MFN,平面MFN,
平面平面BDE,又平面MFN,
则平面BDE;
(2)底面ABC,.
以A为原点,分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系.
,,
0,,0,,4,,0,,2,,2,,
则,,
设平面MEN的一个法向量为,
由,得
取,得.
由图可得平面CME的一个法向量为.
.
由图可知二面角的平面角为锐角,
二面角的余弦值为,则正弦值为;
(3)设,则0,,,.
直线NH与直线BE所成角的余弦值为,
.
解得:.
当H与P重合时直线NH与直线BE所成角的余弦值为,此时线段AH的长为4.
5.已知圆锥的顶点为P,底面圆心为O,半径为2.
(1)设圆锥的母线长为4,求圆锥的体积;
(2)设,OA、OB是底面半径,且,M为线段AB的中点,如图.求异面直线PM与OB所成的角的余弦值.
【答案】(1) ;(2).
【分析】
(1)利用圆锥的体积公式进行求解即可;
(2)建立空间直角坐标系,利用空间向量夹角公式进行求解即可.
【详解】
(1)圆锥的顶点为P,底面圆心为O,半径为2,圆锥的母线长为4,
圆锥的体积
;
(2),OA,OB是底面半径,且,
M为线段AB的中点,
以O为原点,OA为x轴,OB为y轴,OP为z轴,
建立空间直角坐标系,
0,,0,,2,,
1,,0,,
1,,2,,
设异面直线PM与OB所成的角为,
则.
异面直线PM与OB所成的角的余弦值为.
6.如图所示,已知四棱锥中,四边形为正方形,三角形为正三角形,侧面底面,M是棱的中点.
(1)求证:;
(2)求二面角的正弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)取的中点O,连接,并过O点作的平行线,交于E,即可得到,,从而得到底面,如图建立空间直角坐标系,利用空间向量法证明线线垂直;
(2)利用空间向量法求出二面角的余弦值,从而求出其正弦值;
【详解】
解:(1)取的中点O,连接,并过O点作的平行线,交于E,则
∵三角形为正三角形
∴
∵平面底面且平面底面
∴底面
以O为坐标原点,的方向为x轴正方向,建立如图所示空间直角坐标系,令,
则,,,
,
∴
(2),
设平面的一个法向量为
则即
令,
设平面的一个法向量为
则即
令,
所以,
所以
∴二面角的正弦值为
7.已知点,分别是正方形的边,的中点.现将四边形沿折起,使二面角为直二面角,如图所示.
(1)若点,分别是,的中点,求证:平面;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)要证明线面平行,可转化为证明面面平行;
(2)根据面面垂直的性质定理,可知平面,再结合线面角的定义,可得得到直线与平面所成角的正弦值.
【详解】
证明:(1)连接,
设点为的中点,连接,,
在中,又因为点为中点,
所以.
同理可证得,
又因为,分别为正方形的边,的中点,
故,所以.
又因为,所以平面平面.
又因为平面,所以平面.
(2)因为为正方形,,分别是,的中点,
所以四边形为矩形,则.
又因为二面角为直二面角,平面平面,平面,
所以平面,
则为直线在平面内的射影,
因为为直线与平面所成的角.
不妨设正方形边长为,则,
在中,,
因为平面,平面,所以,
在中,,
,
即为直线与平面所成角的正弦值.
8.已知如图1所示,等腰中,,,为中点,现将沿折痕翻折至如图2所示位置,使得,、分别为、的中点.
(1)证明:平面;
(2)求四面体的体积.
【答案】(1)证明见解析;(2).
【分析】
(1)由线面平行的判断定理即得;
(2)根据题意可得,即求
【详解】
(1)证明:
、分别为、的中点,,
平面,平面,
平面;
(2)在原等腰三角形中,,,为中点,
,,且,
在折叠后的三棱锥中,,,
又,平面,
,,
,
,
为中点,,
可得.
9.在三棱柱ABC-A1B1C1中,AB=2,BC=BB1=4,,且∠BCC1=60°.
(1)求证:平面ABC1⊥平面BCC1B1:
(2)设二面角C-AC1-B的大小为θ,求sinθ的值.
【答案】(1)证明见解析;(2).
【分析】
(1)勾股定理证明结合证明即可证明;(2)建立空间坐标系求解
【详解】
解:(1)在中,,所以,即
因为,所以
所以,即
又,所以平面
又平面,所以平面平面.
(2)由题意知,四边形为菱形,且,则为正三角形,取的中点,连接,则
以为原点,以的方向分别为轴的正方向,建立空间直角坐标系,则
设乎面的法向量为,且.
由得取.
由四边形为菱形,得;
又平面,所以;
又,所以平面,
所以平面的法向量为.
所以.
故.
10.如图,四棱锥中,底面是直角梯形,,∠BAD=90°,已知,.
(1)证明:;
(2)若二面角的余弦值为,求四棱锥的体积.
【答案】(1)证明见解析;(2).
【分析】
(1)过作交于点,求得,取中点为点,连接,
证得,证得平面,即可证得.
(2)由(1)知,得到,求得点到平面的距离为,和梯形的面积,结合体积公式,即可求解.
【详解】
(1)过作交于点,则,
在直角中,则,
取中点为点,连接,
因为,所以,
又因为,且平面,所以平面,
又由平面,所以.
(2)由题意知,二面角的余弦值为,
由(1)知,二面角的平面角为,故,
在中,可得,所以,
所以,
设点到平面的距离为,则,
又梯形的面积为,
故四棱锥的体积.
11.如图,四棱柱ABCD—A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
(1)求证:平面CC1D1D⊥底面ABCD;
(2)若平面BCC1B1与平面BED1所成的锐二面角的大小为,求线段ED1的长度.
【答案】(1)证明见解析;(2).
【分析】
(1)利用线面垂直的判定定理证明AD⊥平面CDD1C1,可得AD⊥D1E,又CD⊥D1E,即可证明D1E⊥平面ABCD,再由面面垂直的判定定理证明即可;
(2)D1E=a,建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,然后利用待定系数法求出平面的法向量,由向量的夹角公式列出关于a的方程求解即可.
【详解】
(1)证明:因为底面ABCD和侧面BCC1B1都是矩形,
所以AD⊥CD,AD⊥DD1,
又CD∩DD1=D,CD,DD1⊂平面CDD1C1,
所以AD⊥平面CDD1C1,又D1E⊂平面CDD1C1,
所以AD⊥D1E,又CD⊥D1E,且CD∩AD=D,CD,AD⊂平面ABCD,
故D1E⊥平面ABCD,又D1E⊂平面CC1D1D,
则平面CC1D1D⊥平面ABCD;
(2)解:取AB得中点F,连结EF,则四边形EFBC为正方形,
所以EF⊥CD,故以E为坐标原点,建立空间直角坐标系如图所示,
设D1E=a,则E(0,0,0),F(1,0,0),B(1,1,0),C(0,1,0),C1(0,2,a),
所以,
设平面BCC1B1的法向量为,
则有,即,
令z=1,则,
因为FC⊥BE,又FC⊥D1E,BE∩D1E=E,BE,D1E⊂平面BED1,
所以FC⊥平面BED1,
故为平面BD1E的一个法向量,
所以,
因为平面BCC1B1与平面BED1所成的锐二面角的大小为,
,解得a=1,
所以D1E=1.
12.如图,四棱锥的底面是边长为2的正方形,平面平面,是斜边的长为的等腰直角三角形,,分别是棱,的中点,是棱上一点.
(1)求证:平面平面;
(2)若直线与平面所成角的正切值为,求锐二面角的余弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)根据面面垂直的性质定理,结合线面垂直的判定定理、面面垂直的判定定理进行证明即可;
(2)根据(1),结合线面角的定义得出点是的中点,建立空间直角坐标系,利用空间向量夹角公式进行求解即可.
【详解】
解:(1)依题意可得:,.
∵平面平面,平面平面,,平面,
∴平面,平面∴.
在中,,是棱的中点,所以.
又,,平面,∴平面.
又平面,∴平面平面.
(2)如图,取的中点,连接,,
则,
由(1)知平面,∴平面
∴是直线与平面所成角
∴,
∴,∴
∴是棱的中点,
以为坐标原点,,,分别为轴,轴,轴建立空间直角坐标系,
则有:,,,
∴,,
设平面的法向量为,平面的法向量为
则,令,则
有,令,则
∴
∴锐二面角的余弦值为.
13.如图所示,四棱锥的底面是边长为2的正方形,侧面底面,,F在侧棱上,且平面.
(1)求证:平面;
(2)求点D到平面的距离.
【答案】(1)证明见解析;(2).
【分析】
(1)证得和,结合线面垂直的判定定理即可证得结论;
(2)等体积法即可求出结果.
【详解】
证明:(1)∵侧面底面,侧面底面,且,底面,∴平面,∴,∵平面,平面,故,,故平面;
(2)过点E作,垂足为O,则平面,在中,,可求得,设D到平面的距离为h,由,
所以,,
即点D到平面的距离为.
14.在三棱锥B-ACD中,平面ABD⊥平面ACD,若棱长AC=CD=AD=AB=1,且∠BAD=30°,求点D到平面ABC的距离.
【答案】.
【分析】
建立空间直角坐标系,求出平面ABC的一个法向量,利用空间距离的公式即可求出结果.
【详解】
解 如图所示,以AD的中点O为原点,以OD,OC所在直线为x轴、y轴,过O作OM⊥平面ACD交AB于M,以直线OM为z轴建立空间直角坐标系,
则A,B,C,D,
∴=,=,=,
设=(x,y,z)为平面ABC的一个法向量,
则,所以y=-x,z=-x,可取=(-,1,3),
代入d= ,得d==,
即点D到平面ABC的距离是.
15.如图,在长方体中,,,为棱的中点.
(1)证明:平面;
(2)求二面角的大小.
【答案】(1)证明见解析;(2).
【分析】
(1)根据侧平面得出,再利用勾股定理即可证明,从而证明平面.
(2)以点为坐标原点,以分别为轴,建立空间直角坐标系,利用向量法即可解决.
【详解】
(1)证明:因为是长方体,所以侧平面,
而平面,所以,
在中,,
所以,所以,
又,平面,因此平面.
(2)如图所示,以点为坐标原点,以分别为轴,建立空间直角坐标系,
则,
,
设是平面的法向量,
则,
设是平面的法向量,
则,
所以,因为二面角为钝角,所以二面角的大小为.
16.如下图,在四棱锥中,底面是正方形,平面平面,,.
(1)求与所成角的余弦值;
(2)求证:.
【答案】(1);(2)证明见解析.
【分析】
(1)由题意可得 即为SA 与 BC所成的角,根据余弦定理计算即可;
(2)结合面面垂直的性质和线面垂直的性质即可证明.
【详解】
【考查内容】异面直线所成的角,直线与平面垂直的判定和性质
【解】(1)因为,因此即为与所成的角,在中,,
又在正方形中,因此,
因此与所成角的余弦值是.
(2)因为平面平面,平面平面,在正方形中,,
因此平面,又因为平面,因此.
17.如图,四棱锥的底面是矩形,底面,M为的中点,且.
(1)证明:平面平面;
(2)若,求四棱锥的体积.
【答案】(1)证明见解析;(2).
【分析】
(1)由底面可得,又,由线面垂直的判定定理可得平面,再根据面面垂直的判定定理即可证出平面平面;
(2)由(1)可知,,由平面知识可知,,由相似比可求出,再根据四棱锥的体积公式即可求出.
【详解】
(1)因为底面,平面,
所以,
又,,
所以平面,
而平面,
所以平面平面.
(2)由(1)可知,平面,所以,
从而,设,,
则,即,解得,所以.
因为底面,
故四棱锥的体积为.
18.如图,在四棱锥中,底面是平行四边形,,M,N分别为的中点,.
(1)证明:;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)要证,可证,由题意可得,,易证,从而平面,即有,从而得证;
(2)取中点,根据题意可知,两两垂直,所以以点为坐标原点,建立空间直角坐标系,再分别求出向量和平面的一个法向量,即可根据线面角的向量公式求出.
【详解】
(1)在中,,,,由余弦定理可得,
所以,.由题意且,平面,而平面,所以,又,所以.
(2)由,,而与相交,所以平面,因为,所以,取中点,连接,则两两垂直,以点为坐标原点,如图所示,建立空间直角坐标系,
则,
又为中点,所以.
由(1)得平面,所以平面的一个法向量
从而直线与平面所成角的正弦值为.
19.如图,
(I)求证
(II)设
【答案】见解析
【详解】
(I),
,
(II)
,,
20.如图,在四棱锥中,底面,,点在线段上,且.
(Ⅰ)求证:平面;
(Ⅱ)若,,,,求四棱锥的体积.
【答案】(Ⅰ)证明见解析 (Ⅱ)
【分析】
(Ⅰ)由已知可得,,即可证明结论;
(Ⅱ)底面,,根据已知条件求出梯形面积,即可求解.
【详解】
(Ⅰ)证明:因为底面,平面,
所以.因为,,
所以.又,
所以平面.
(Ⅱ)解:由(Ⅰ)可知,
在中,,
,
又因为,则.
又,,
所以四边形为矩形,四边形为梯形.
因为,所以,
,
,
于是四棱锥的体积为.
21.如图,直三棱柱,,点M,N分别为和的中点.
(Ⅰ)证明:∥平面;
(Ⅱ)若二面角为直二面角,求的值.
【答案】(Ⅰ)见解析 (Ⅱ)
【详解】
试题分析:(Ⅰ)分别取的中点,再连结,则有
,,所以
则四边形为平行四边形,所以,则∥平面
(Ⅱ)分别以所在直线为轴,建立空间直角坐标系(如图)
设,则,
设平面的一个法向量,
由得平面的一个法向量,
同理可得平面的一个法向量,
因为二面角A为直二面角,所以,则有
22.如图,在三棱锥中, 侧面与侧面均为等边三角形,为中点.
(Ⅰ)证明:平面
(Ⅱ)求二面角的余弦值.
【答案】(Ⅰ)平面
(Ⅱ)二面角的余弦值为
【详解】
证明:
(Ⅰ)由题设AB=AC=SB=SC=SA. 连结OA,△ABC为等腰直角三角形,所以OA=OB=OC=SA,且AO⊥BC. 又△SBC为等腰三角形,故SO⊥BC,
SO=SA,
从而OA2+SO2=SA2,
所以△SOA为直角三角形,.
又AO∩BC=O,
所以SO⊥平面ABC.
(Ⅱ)解法一:
取SC中点M, 连结AM,OM, 由(Ⅰ)知, 得OM⊥SC,AM⊥SC.
为二面角的平面角.
由AO⊥BC,AO⊥SO,SO∩BC得
AO⊥平面SBC,
所以AO⊥OM. 又,故
所以二面角的余弦值为
解法二:
以O为坐标原点,射线OB、OA分别为x轴、y轴的正半轴,建立如图的空间直角坐标系
设B(1,0,0),则
SC的中点
,.
故MO⊥SC,MA⊥SC,等于二面角的平面角.
所以二面角的余弦值为
23.如图,在四棱锥P—ABCD中,底面是边长为的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA= ,M,N分别为PB,PD的中点.
(1)证明:MN∥平面ABCD;
(2) 过点A作AQ⊥PC,垂足为点Q,求二面角A—MN—Q的平面角的余弦值.
【答案】(1)见解析;(2) .
【分析】
(1)证明:连接BD,因为M、N分别是PB、PD的中点,所以MN是△PBD的中位线,所以MN∥BD.
又因为MN⊄平面ABCD,BD⊂平面ABCD,
所以MN∥平面ABCD.
(2)解: 在菱形ABCD中,∠BAD=120°,
得AC=AB=BC=CD=DA,
BD=AB.
又因为PA⊥平面ABCD,
所以PA⊥AB,PA⊥AC,
PA⊥AD.
所以PB=PC=PD.
所以△PBC≌△PDC.
而M、N分别是PB、PD的中点,
所以MQ=NQ,
且AM=PB=PD=AN.
取线段MN的中点E,连接AE,EQ,
则AE⊥MN,QE⊥MN,
所以∠AEQ为二面角AMNQ的平面角.
由AB=2,PA=2,故在△AMN中,AM=AN=3,MN=BD=3,得AE=.
在直角△PAC中,AQ⊥PC,得AQ=2,QC=2,PQ=4,
在△PBC中,cos∠BPC==,
得MQ==.
在等腰△MQN中,MQ=NQ=,MN=3,
得QE==.
在△AEQ中,AE=,QE=,AQ=2,
得cos∠AEQ==.
所以二面角AMNQ的平面角的余弦值为.
24.如图,在三棱锥中,,,为的中点.
(1)证明:平面;
(2)若点在棱上,且,求点到平面的距离.
【答案】(1)详见解析(2).
【详解】
分析:(1)连接,欲证平面,只需证明即可;(2)过点作,垂足为,只需论证的长即为所求,再利用平面几何知识求解即可.
详解:(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=.
连结OB.因为AB=BC=,所以△ABC为等腰直角三角形,且OB⊥AC,OB==2.
由知,OP⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,所以CH⊥平面POM.
故CH的长为点C到平面POM的距离.
由题设可知OC==2,CM==,∠ACB=45°.
所以OM=,CH==.
所以点C到平面POM的距离为.
点睛:立体几何解答题在高考中难度低于解析几何,属于易得分题,第一问多以线面的证明为主,解题的核心是能将问题转化为线线关系的证明;本题第二问可以通过作出点到平面的距离线段求解,也可利用等体积法解决.
25.如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
【答案】(1)证明见解析;(2)证明见解析;(3)
【详解】
试题分析:(Ⅰ)要证明线线垂直,一般转化为证明线面垂直;(Ⅱ)要证明面面垂直,一般转化为证明线面垂直、线线垂直;(Ⅲ)由即可求解.
试题解析:(I)因为,,所以平面,
又因为平面,所以.
(II)因为,为中点,所以,
由(I)知,,所以平面.
所以平面平面.
(III)因为平面,平面平面,
所以.
因为为的中点,所以,.
由(I)知,平面,所以平面.
所以三棱锥的体积.
26.如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=AD.
(Ⅰ)在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;
(Ⅱ)证明:平面PAB⊥平面PBD.
【答案】(Ⅰ)详见解析;(Ⅱ)详见解析.
【详解】
试题分析:本题考查线面平行、线线平行、线线垂直、线面垂直等基础知识,考查空间想象能力、分析问题的能力、计算能力.第(Ⅰ)问,先证明线线平行,再利用线面平行的判定定理证明线面平行;第(Ⅱ)问,先由线面垂直得到线线垂直,再利用线面垂直的判定定理得到BD⊥平面PAB,最后利用面面垂直的判定定理证明面面垂直.
试题解析:
(Ⅰ)取棱AD的中点M(M∈平面PAD),点M即为所求的一个点.理由如下:
因为AD∥BC,BC=AD,所以BC∥AM, 且BC=AM.
所以四边形AMCB是平行四边形,从而CM∥AB.
又AB平面PAB,CM平面PAB,
所以CM∥平面PAB.
(说明:取棱PD的中点N,则所找的点可以是直线MN上任意一点)
(Ⅱ)由已知,PA⊥AB, PA⊥CD,
因为AD∥BC,BC=AD,所以直线AB与CD相交,
所以PA⊥平面ABCD.
从而PA⊥BD.
因为AD∥BC,BC=AD,
所以BC∥MD,且BC=MD.
所以四边形BCDM是平行四边形.
所以BM=CD=AD,所以BD⊥AB.
又AB∩AP=A,所以BD⊥平面PAB.
又BD平面PBD,
所以平面PAB⊥平面PBD.
27.如图,在三棱台ABC–DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
(Ⅰ)求证:BF⊥平面ACFD;
(Ⅱ)求直线BD与平面ACFD所成角的余弦值.
【答案】(1)证明详见解析;(2).
【详解】
试题分析:本题主要考查空间点、线、面位置关系,线面角等基础知识,同时考查空间想象能力和运算求解能力.
试题解析:(Ⅰ)延长相交于一点,如图所示.
因为平面平面,且,所以
平面,因此,.
又因为,,,所以
为等边三角形,且为的中点,则
所以平面.
(Ⅱ)因为平面,所以是直线与平面所成的角.
在中,,得.
所以,直线与平面所成的角的余弦值为.
28.如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且 ,.
求证:(1)直线DE平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
【答案】(1)详见解析(2)详见解析
【详解】
试题分析:(1)利用线面平行判定定理证明线面平行,而线线平行的寻找往往结合平面几何的知识,如中位线的性质等;(2)利用面面垂直判定定理证明,即从线面垂直出发给予证明,而线面垂直的证明,往往需要多次利用线面垂直性质定理与判定定理.
试题解析:证明:(1)在直三棱柱中,
在三角形ABC中,因为D,E分别为AB,BC的中点,
所以,于是,
又因为DE平面平面,
所以直线DE//平面.
(2)在直三棱柱中,
因为平面,所以,
又因为,
所以平面.
因为平面,所以.
又因为,
所以.
因为直线,所以
29.如图,在三棱锥中,在底面ABC的射影为BC的中点,D为的中点.
(1)证明:;
(2)求直线和平面所成的角的正弦值.
【答案】(1)见解析;(2)
【详解】
(1)利用线面垂直的定义得到线线垂直,根据线面垂直的判定证明直线与平面垂直;
(2)通过添加辅助线,证明平面,以此找到直线与平面所成角的平面角,在直角三角形中通过确定边长,计算的正弦值.
试题解析:(1)设为中点,由题意得平面,所以.
因为,所以.
所以平面.
由,分别为的中点,得且,从而且,
所以是平行四边形,所以.
因为平面,所以平面.
(2)作,垂足为,连结.
因为平面,所以.
因为,所以平面.
所以平面.
所以为直线与平面所成角的平面角.
由,得.
由平面,得.
由,得.
所以
30.如图,在四棱锥中,底面,,是的中点.
(Ⅰ)证明;
(Ⅱ)证明平面;
(Ⅲ)求二面角的大小.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ)
【分析】
(1)证得平面 ,结合线面垂直的性质定理即可得出结论;
(2)证得和,结合线面垂直的判定定理即可得出结论;
(3)作出辅助线,证得是二面角 的平面角.进而在中,即可求出其正弦值,进而求出结果.
【详解】
(Ⅰ)证明:在四棱锥中,因 底面, 平面,故 . ,平面 .
而平面 ,所以.
(Ⅱ)证明: ,所以,又因为是的中点,所以,由(Ⅰ)知,且,所以平面 ,
又因为平面 ,所以,又因为因 底面, 平面,故 ,又因为,且,所以底面,且平面 ,所以,又因为,所以平面.
(Ⅲ)
过点作 ,垂足为,连结 .则(Ⅱ)知平面 ,
在平面内的射影是,则.
因此是二面角 的平面角.
由已知,得,设,可得,
在中, 因为,,
则.
在中,.
所以二面角的大小是.
(中级)30-70题
31.如图,在四棱锥P-ABCD中,底面ABCD为菱形,△PAD为正三角形,平面PAD⊥平面ABCD,E,F分别是AD,CD的中点.
(1)证明:BD⊥PF;
(2)若AD=DB=2,求点C到平面PBD的距离;
【答案】
(1)证明见解析
(2)
【分析】
(1)连接AC,证得EFAC, 利用面面垂直的性质定理,证得PE⊥平面ABCD,进而证得BD⊥平面PEF,即可得到BD⊥PF.
(2)设点到平面的距离为,结合,即可求解.
(1)
证明:连接AC,因为在中,E,F分别是AD,CD的中点,所以EFAC,
又因为在菱形ABCD中,可得AC⊥BD,所以BD⊥EF,
因为为正三角形,E为AD中点,所以PE⊥AD,
又因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以PE⊥平面ABCD,
又BD⊂平面ABCD,所以PE⊥BD,
因为PE∩EF=E,所以BD⊥平面PEF,
又PF⊂平面PEF,所以BD⊥PF.
(2)
解:设点到平面的距离为,
由,可得,
在正三角形中,;
在菱形中,因为,所以为正三角形,
所以,
在中,,所以,
所以,
即点到平面的距离.
32.如图,在四棱锥P-ABCD中,底面ABCD为菱形,△PAD为正三角形,平面PAD⊥平面ABCD,E,F分别是AD,CD的中点.
(1)证明:BD⊥PF;
(2)若∠BAD=60°,求直线PC与平面PBD所成角的正弦值;
【答案】
(1)证明见解析
(2)
【分析】
(1)连接AC,菱形中易得,再由面面垂直的性质定理得平面,从而得,则可证得线面垂直,从而有线线垂直;
(2)以E为原点,建立如图所示的空间直角坐标系,用空间向量法求线面角.
(1)
连接AC,因为在△ADC中,E,F分别是AD,CD的中点,所以EF//AC,
又因为在菱形ABCD中AC⊥BD,所以BD⊥EF;
因为△PAD为正三角形,E为AD中点,所以PE⊥AD;
又因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,平面,
所以PE⊥平面ABCD,又BD⊂平面ABCD,所以PE⊥BD;
因为PE∩EF=E,平面PEF,所以BD⊥平面PEF,
又PF⊂平面PEF,所以BD⊥PF;
(2)
连接BE,因为∠BAD=60°,所以△ADB为等边三角形,所以BE⊥AD;
由(1)知,PE⊥平面ABCD,故以E为原点,建立如图所示的空间直角坐标系
设AD=2,则
则
设平面PBD的法向量为,则,可取
所以,故直线PC与平面PBD所成角的正弦值为.
33.如图,在四棱锥E-ABCD中,ABCE,AECD,,AB=3,CD=4,AD=2BC=10.
(1)证明:∠AED是锐角;
(2)若AE=10,求二面角A-BE-C的余弦值.
【答案】
(1)证明见解析
(2)
【分析】
(1)延长AB、DC交于点M,结合已知条件利用线面垂直判定定理和性质证明平面,然后利用勾股定理和余弦定理即可证明;
(2)结合已知条件建立空间直角坐标系,分别求出平面和平面的法向量,然后利用二面角的空间向量公式求解即可.
(1)
延长AB、DC交于点M,连接EM,如下图所示:
因为,,所以为的中位线,
从而,,,
所以,故,
又因为ABCE,AECD,,,
所以平面,平面,
因为平面,平面,
所以,,
因为,所以平面,
令,则,,
所以,
所以是锐角.
(2)
以为坐标原点,建立如下图的空间直角坐标系:
由题意可知,,,,,,,
故,,,
设平面的法向量为,
由,令,则,,
从而,
因为平面,所以是平面的一个法向量,
由图可知,二面角为钝二面角,
故,
从而二面角A-BE-C的余弦值.
34.如图,在直四棱柱中,
(1)若为的中点,试在上找一点,使平面;
(2)若四边形是正方形,且与平面所成角的余弦值为,求二面角的余弦值.
【答案】
(1)点为的中点
(2)
【分析】
(1)当点为的中点时平面,连接,可得,再由棱柱的性质得到,即可得到,从而得证;
(2)建立空间直角坐标系,设正方形的边长为,,利用空间向量法表示出与平面所成角的正弦值,即可求出,从而求出二面角的余弦值;
(1)
解:当点为的中点时平面,
证明如下:连接,∵、分别为、的中点,∴,
在直四棱柱中,,
∴,∵平面,平面,∴平面;
(2)
解:以为坐标原点,、、的方向分别为、、轴的正方向,
建立空间直角坐标系,如图所示,
设正方形的边长为,,则、、,
则、,设为平面的法向量,
则,即,令,则、,即,
与平面所成角的余弦值为,
与平面所成角的正弦值为,且,
∴,解得,∴,
又平面的一个法向量为,
∴,
设二面角的平面角为,为锐角,则.
35.如图1,已知为等边三角形,四边形为平行四边形,,把沿向上折起,使点E到达点P位置,如图2所示;且平面平面.
(1)证明:;
(2)在(1)的条件下求二面角的余弦值.
【答案】
(1)证明见解析
(2)
【分析】
(1)先由平面平面,证明,再由勾股定理证明,最后由判定定理以及性质证明;
(2)建立空间直角坐标系,利用向量法得出二面角的余弦值.
(1)
证明:如图,设的中点为F,连接.
∵为等边三角形,∴.
又平面平面,平面平面,
∴平面.
∵平面,∴.
∵,
∴,∴.
又,∴平面.
又∵平面,∴.
(2)
由(1)知平面,则平面平面.
设中点为O,连接,则.
又平面平面,平面平面,∴平面.
设中点为,连接.
∵,∴,
故以点O为坐标原点,,,所在直线分别为x,y,z轴建立空间直角坐标系如图所示,
则,
∴,
.
设平面的法向量为,
由得取,则
设平面的法向量为,
由得取,则,
∴二面角的余弦值为
36.如图所示,在四棱锥中,平面,,四边形为梯形,,,,,,,点在上,满足.
(1)求证:平面平面;
(2)若点为的中点,求平面与平面所成角的余弦值.
【答案】
(1)证明见解析
(2)
【分析】
(1)求出可得可得结合可证明面,再由面面垂直的判定定理即可求证;
(2)如图建立空间直角坐标系,求出平面与平面的法向量,由空间向量夹角公式即可求解.
(1)
因为,,,所以,
因为,所以,可得,
因为平面,平面,所以,
因为,所以面,
因为面,所以平面平面.
(2)
因为,,所以四边形是平行四边形,
所以,,,
如图:以为原点,分别以,所在的直线为,轴,过点垂直于面的直线为轴建立空间直角坐标系,则,,,,,所以,,,,
设平面的法向量,
由,令,则,,
所以
设平面的法向量,
由,令,则,,
所以,
所以.
37.在四棱锥中,平面,,,,为的中点,在平面内作于点.
(1)求证:平面平面;
(2)求二面角的余弦值.
【答案】
(1)证明见解析
(2)
【分析】
(1)证明出平面,,可得出平面,再利用面面垂直的判定定理可证得结论成立;
(2)以点为坐标原点,、、分别为、、的正方向建立空间直角坐标系,利用空间向量法可求得二面角的余弦值.
(1)
证明:平面,平面,,
,,平面,
平面,,
,、平面,,平面,
平面,所以,平面平面,
平面平面.
(2)
,以点为坐标原点,、、的方向 分别为、、的正方向建立如下图所示的空间直角坐标系,
则、、、、,
,,设平面的法向量为,
则,取,可得,
,设平面的法向量为,
则,取,可得,
,
由图形可知,二面角的平面角为锐角,
因此,二面角的余弦值为.
38.在正方体中,点、分别在、上,且,.
(1)求证:;
(2)求直线与平面所成角的正弦值.
【答案】
(1)证明见解析;
(2).
【分析】
(1)以为轴,为轴,为轴建立空间直角坐标系,设正方体的棱长为,写出各点坐标并得出,,根据空间向量的数量积运算求得,即可证出;
(2)设平面的法向量为,直线与平面所成角为,利用空间向量法求出,再根据空间向量法求线面夹角的公式,即可求出直线与平面所成角的正弦值.
(1)
证明:以为轴,为轴,为轴建立空间直角坐标系,
因为,,设正方体的棱长为,
则点,
则,,
所以,即.
(2)
解:设平面的法向量为,直线与平面所成角为,
,,
由,得,
令,得,则,
所以,
所以直线与平面所成角的正弦值为.
39.如图,在多面体中,均垂直于平面,,,,.
(1)证明:平面;
(2)求与平面所成角的余弦值.
【答案】
(1)证明见解析
(2)
【分析】
(1)连接易得为平行四边形,即,根据线面垂直的性质及判定即可证结论.
(2)法一:过作于,延长至使,过作交于,连接,根据线面垂直的性质及判定、平行四边形的性质证面,进而确定线面角的平面角,即可求余弦值;法二:构建空间直角坐标系,分别求出的方向向量和面的一个法向量,利用空间向量夹角的坐标表示求线面角的余弦值.
(1)
连接,由且,
∴四边形为平行四边形,即,
由为等腰梯形,结合题设:,,则.
由平面,平面,则,又,
∴平面,故平面.
(2)
法一:过作于,延长至使,过作交于,连接,
面,面,则,又,,
面,
即为平行四边形,
则四边形为平行四边形,
面,则即为所求线面角,
由题意:,,,.
在梯形中,易得,所以,得,则,
在中,易得,则.
∴.
法二:以为原点,为轴,为轴,作轴,建立空间直角坐标系,
易得,,,,
,,,
设面的一个法向量为, 由,可得,
记与面所成角为,,
,即与面所成角的余弦值为 .
40.某商品的包装纸如图1,其中菱形的边长为3,且,,,将包装纸各三角形沿菱形的边进行翻折后,点E,F,M,N汇聚为一点P,恰好形成如图2的四棱锥形的包裹.
(1)证明底面;
(2)设点T为BC上的点,且二面角的正弦值为,试求PC与平面PAT所成角的正弦值.
【答案】
(1)证明见解析
(2)
【分析】
(1)由翻折之前的边长关系得,,进而得翻折后有,,进而得底面;
(2)解法一:以点A为原点,AB为x轴,过点A作AB的垂线为y轴,AP为z轴建立空间直角坐标系,进而得为二面角的平面角,再结合正弦定理得,再写坐标,利用坐标法求解即可.
解法二:由(1)知为二面角的平面角,即,进而由正弦定理得,再由余弦定理可得,设过点C作平面PAT的垂线,垂足为Q,连接PQ,所以为PC与面PAT所成角,再利用得,进而得答案;
解法三:由(1)得为二面角的平面角,即,进而得,,再过点C作CQ垂直于AT于Q,连接CQ、AC
进而证明面PAT,再根据几何关系求解即可.
(1)
由菱形的边长为3,,
可得:,即有
同理,即有
在翻折的过程中,垂直关系保持不变可得:,,.
可得底面
(2)
解法一:如图,以点A为原点,AB为x轴,过点A作AB的垂线为y轴,AP为z轴建立空间直角坐标系.
由第(1)问可得底面,可得:,.
则为二面角的平面角,由题意可得:
考虑,,可得.
利用正弦定理
可得:,可得点T的坐标为.
点,,
设面的法向量为,则有,即:.
令,则有,
则有:
则PC与面PAT所成角的正弦值为.
解法二:由第(1)问可知底面,,
所以,,.
则为二面角的平面角,由题意可得:
考虑,,可得.
利用正弦定理
可得:,即点T为BC上靠近点B的三等分点
所以在中,由余弦定理可得:,
设过点C作平面PAT的垂线,垂足为Q,连接PQ,
所以为PC与面PAT所成角
考虑三棱锥,由于,
,
因为,所以
所以
所以PC与面PAT所成角的正弦值为
解法三:由面,可得:,.
故为二面角的平面角,由题意可得:
因为为锐角,所以
故
过点C作CQ垂直于AT于Q,连接CQ、AC
则
∵,∴
∵面,∴
又因为,,故面PAT
故为与面PAT所成的角,∴
即PC与面PAT所成角的正弦值为
41.如图,在四棱锥中,底面是菱形,侧面底面,且PA=AB, .
(1)证明:;
(2)若,求直线与平面所成角的正弦值.
【答案】
(1)证明见解析
(2)
【分析】
(1)要证明,只需证明平面即可;
(2)由(1)可得平面平面,所以为直线与平面所成角,在三角形POC中由正弦定理即可得到答案.
(1)
证明:
∵侧面底面,
∴底面
∴
如图,连接,交于,
∵四边形是菱形 ∴
又
∴平面,因为平面,
∴
(2)
连接,由(1)知平面,又平面,
∴ 平面平面,
∴ 为直线与平面所成角
设,由知,
在中,,
在中,由正弦定理,,
即.
42.1.如图,正方形所在平面与等边所在平面成的锐二面角为,设平面与平面相交于直线.
(1)求证:;
(2)求直线与平面所成角的正弦值.
【答案】
(1)证明见解析
(2)
【分析】
(1)利用线面平行的判定及线面平行的性质来证明;(2)建立空间直角坐标系解决线面角的正弦值.
(1)
因为CD//AB,平面ABE,所以CD//平面ABE
又面ABE平面CDE=l,所以l//CD
(2)
如图建立空间直角坐标系,设AE=2,则
所以A(1,0,0),B(1,0,0),E(0,,0),C(1,1,),D(1,1,),
所以=(1,,0),=(0,1,),
设平面BCE的法向量为(x,y,z),则
取,则,
故平面BCE的法向量为,
又
设直线DE与平面BCE所成角为,
则
43.如图,在四棱锥中,,,平面平面ABCD,点E在AD上,且,.
(1)求证:.
(2)设平面平面,求二面角的余弦值.
【答案】
(1)证明见解析
(2)
【分析】
(1)由,→四边形ABCE是平行四边形→,结合,再由面面垂直性质得平面APD→;
(2)延长AB,DC交于点Q,连接PQ→直线PO就是交线l→二面角就是二面角,结合建系法,以E为坐标原点,直线EC,ED,EP分别为x轴、y轴、z轴建立空间直角坐标系,分别求出平面ABP,平面PEQ的法向量,结合向量夹角的余弦公式即可求解.
(1)
在四边形ABCD中,,,
所以四边形ABCE是平行四边形,所以.
因为,所以,
因为平面平面ABCD,平面平面,
所以平面APD,
又平面APD,所以;
(2)
延长AB,DC交于点Q,连接PQ,则直线PQ就是交线l,(突破:通过作辅助线找到两平面的交线),
连接EP,EQ,则二面角就是二面角.
因为,且,所以B为AQ的中点.
设,则在△PAD中,,,所以,
则,平面ABCD,
由(1)可知,故以E为坐标原点,直线EC,ED,EP分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则,,,,,所以,,,.
设平面ABP的法向量为,则,,
可得,即,取,则,
故为平面ABP的一个法向量,
设平面PEQ的法向量为,则,,
可得,即,
取,则,故为平面PEQ的一个法向量,
所以.
由图易知,二面角为锐二面角,所以二面角的余弦值为.
44.如图,在四棱锥中,底面是平行四边形,,,M,N分别为,的中点,.
(1)证明:;
(2)若,求直线与平面所成角的正弦值.
【答案】(1)答案见解析(2)
【分析】
(1)要证,可证,由题意可得,,又,从而平面,即有,再由,可得平面从而得证;
(2)取中点,根据题意可知,两两垂直,所以以点为坐标原点,建立空间直角坐标系,再分别求出向量和平面的一个法向量,即可根据线面角的向量公式求出.
【详解】
(1)底面是平行四边形,,
,
又,,
由余弦定理可得,
,
,又,,
平面,又平面,
,又,
平面,
平面
(2)连接,在中,,
由余弦定理可知,,即,
在中,,
取中点,连接,则两两垂直,
以点为坐标原点,如图所示,建立空间直角坐标系, 如图,
则,
所以,
又为中点,所以.
设平面的一个法向量,
则,即,令,则,
所以
从而直线与平面所成角的正弦值为.
45.如图,已知点在圆柱的底面圆上,,圆的直径,圆柱的高.
(1)求点到平面的距离;
(2)求二面角的余弦值大小.
【答案】(1);(2).
【分析】
(1)根据等体积法,由即可求出点到平面的距离;
(2)先证明,,由线面垂直的判定定理可得面,进而可得即为所求二面角的平面角,在中,计算即可求解.
【详解】
(1)因为,,
所以,
在中,由余弦定理可得:,
所以,,
在中,由余弦定理可得,
所,
所以,
设点到平面的距离为,
由,得,
即,
解得:,
所以点到平面的距离为;
(2)二面角即二面角,
因为是圆的直径,点在圆柱的底面圆上,所以,
因为面,面,可得,
因为,所以面,
因为面,面,所以,,
所以即为二面角的平面角,
在中,,,
所以,
所以二面角的余弦值为.
46.如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=2,点P为棱B1C1的中点,点Q为线段A1B上的一动点.
(1)求证:当点Q为线段A1B的中点时,PQ⊥平面A1BC;
(2)设=λ,试问:是否存在实数λ,使得平面A1PQ与平面B1PQ的夹角的余弦值为?若存在,求出这个实数λ;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,λ=或λ=.
【分析】
(1)由题易知PQ∥AC1,利用线面垂直的判定定理可证AC1⊥平面A1BC,即得;
(2)利用坐标系,结合条件可求.
【详解】
(1)连接AB1,AC1,
∵点Q为线段A1B的中点,四边形A1B1BA为矩形,
∴A,Q,B1三点共线,且点Q为AB1的中点.
∵点P,Q分别为B1C1和AB1的中点,
∴PQ∥AC1.
在直三棱柱ABC-A1B1C1中,AC⊥BC,
∴BC⊥平面ACC1A1,
又AC1⊂平面ACC1A1,∴BC⊥AC1.
又AC=AA1,∴四边形ACC1A1为正方形,
∴AC1⊥A1C.
∵A1C∩BC=C,∴AC1⊥平面A1BC.
而PQ∥AC1,∴PQ⊥平面A1BC.
(2)以C为原点,分别以CA,CB,CC1所在直线为x轴,y轴,z轴建立空间直角坐标系,连接A1P,B1Q,BP,则B(0,2,0),A1(2,0,2).设Q(x,y,z).
∵=λ ,∴(x,y-2,z)=λ(2,-2,2).
∴∴Q(2λ,2-2λ,2λ).
∵点Q在线段A1B上运动,
∴平面A1PQ的法向量即为平面A1PB的法向量.
设平面A1PB的法向量为=(x1,y1,z1),
∵C(0,0,0),P(0,1,2),
∴=(0,-1,2),=(2,-1,0).
由得
令y1=2,得=(1,2,1).
设平面B1PQ的法向量为=(x2,y2,z2),
∵B1(0,2,2),∴=(0,1,0),=(2λ,-2λ,2λ-2).
由得
令z1=λ,得=(1-λ,0,λ).
由题意得|cos|===,
∴9λ2-9λ+2=0,解得λ=或λ=.
∴当λ=或λ=时,平面A1PQ与平面B1PQ所成夹角的余弦值为.
47.如图,在三棱锥中,底面,,,.
(1)求证:平面平面;
(2)若二面角的大小为,过点作于,求直线与平面所成角的大小.
【答案】(1)证明见解析;(2)60°.
【分析】
(1)根据根据线面垂直的判断得平面,进而证明平面平面;
(2)解法一:根据题意得,进而过点作于,则平面且为中点,连接,则为直线与平面所成的角,再根据几何关系求解即可;
解法二:建立空间直角坐标系,利用坐标法求解即可.
【详解】
(1)因为底面,所以,
又,所以,
又,为平面内的两条相交直线,
所以平面,
因为平面,
所以平面平面;
(2)解法一:由(1)可知,为二面角的平面角,所以,
又,,,所以,
过点作于,则平面且为中点,连接,
则为直线与平面所成的角,
在中,,,
所以,
故,
所以直线与平面所成的角为60°.
解法二:建立如图所示的空间直角坐标系,
则由已知,可得,,,,
设,(),则,,,
因为,,,
所以,
解得,所以,故,
设平面的法向量为,因为,,
由,得,
令,则,
所以为平面的一个法向量,
所以,
故直线与平面所成的角的正弦值为,
所以直线与平面所成的角为60°.
48.如图,在四棱锥中,平面,底面是菱形,,.
(1)求证:直线平面;
(2)设点在线段上,且二面角的余弦值为,求点到底面的距离.
【答案】(1)证明见解析;(2)或者.
【分析】
(1)由题意利用线面垂直的判定定理即可证得题中的结论;
(2)设,由题意结合空间直角坐标系求得的值即可确定点到底面的距离.
【详解】
(1)由菱形的性质可知,
因为平面
所以,且,
所以直线平面;
(2)以点A为坐标原点,AD,AP方向为y轴,z轴正方向,
如图所示,在平面ABCD内与AD垂直的方向为x轴正方向,
建立如图所示的空间直角坐标系,
设,且,
由于,
故:,据此可得:,
即点M的坐标为,
设平面CMB的法向量为:,则:
,
据此可得平面CMB的一个法向量为:,
设平面MBA的法向量为:,则:
,
据此可得平面MBA的一个法向量为:,
二面角的余弦值为,故:,
整理得,
解得:.
由点M的坐标为或.
易知点到底面的距离为或者.
49.如图,在三棱锥中,底面是边长2的等边三角形,,点F在线段BC上,且,为的中点,为的中点.
(Ⅰ)求证://平面;
(Ⅱ)若二面角的平面角的大小为,求直线与平面所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ).
【分析】
(Ⅰ) 取的中点,连接、,即可证明,,从而得到面面,即可得证;
(Ⅱ) 连接,为二面角的平面角,如图建立空间直角坐标系,利用空间向量法求出线面角的正弦值;
【详解】
解:(Ⅰ)取的中点,连接、,因为为的中点,为的中点,所以,,又,所以,因为面,面,面,所以面,面,又,面,所以面面,因为面,所以平面;
(Ⅱ)连接,因为底面是边长2的等边三角形,,所以,,所以为二面角的平面角,即,如图建立空间直角坐标系,则,,,,,所以,,,设面的法向量为,则,令,则,,所以,设直线与平面所成角为,所以
故直线与平面所成角的正弦值为;
50.如图,直四棱柱的底面是菱形,侧面是正方形,,经过对角线的平面和侧棱相交于点,且.
(1)求证:平面平面;
(2)求二面角的余弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)延长和的延长线相交于点,连接,设四棱柱的棱长为,推导出,由四棱柱的性质得平面,从而平面,由此能证明平面平面;(2)建立空间直角坐标系,写出对应点的坐标,求解平面的法向量,利用向量夹角的计算公式求解即可.
【详解】
(1)如图所示,延长和的延长线相交于点,连接.
设四棱柱的棱长为,
因为,,所以.
由,得,
由余弦定理,得,.
因为,所以,.
又是直四棱柱,故平面.
又平面,所以.
因为,所以平面.
又平面,所以平面平面.
(2)以为坐标原点,,所在直线分别为轴、轴,平行于的直线为轴建立空间直角坐标系,则,,.
设平面的法向量为,则,
即,不妨设,
由(1)得,,平面的一个法向量为.
设二面角的平面角为,则,且由题图知为锐角,所以二面角的余弦值为.
51.直角梯形绕直角边旋转一周的旋转的上底面面积为,下底面面积为,侧面积为,且二面角为,,分别在线段,上.
(Ⅰ)若,分别为,中点,求与所成角的余弦值;
(Ⅱ)若为上的动点、为的中点,求与平面所成最大角的正切值,并求此时二面角的余弦值.
【答案】(Ⅰ);(Ⅱ),.
【分析】
(Ⅰ)设出圆台上、下底面半径,求出圆台高,再利用直二面角建立合适的空间直角坐标系,即可求解;(Ⅱ)取的中点,连接,,,由线线平行与线面垂直性质,即可求解最大值,再利用空间向量法即可求解二面角的余弦值.
【详解】
(Ⅰ)设圆台上、下底面半径分别为,.
∵,∴;∵,∴.
∵,∴.
过点作于点,则,
,∴圆台的高为.
∵二面角是直二面角,
∴建立空间直角坐标系如图所示,
点,,,,,
∴,
∴与所成角的余弦值为.
(Ⅱ)取的中点,连接,,,
∴,则.
∵平面,∴平面,
∴为直线与平面所成角,,
当时,最小,最大.
在中,,,,,
,即与平面所成最大角的正切值为.
又点,,,,
设点,平面的法向量,,,即,∴,
则,,,即,
解得,.
即令得.
易知平面的一个法向量为,
设二面角的平面角为,
则.
由图易得二面角为锐二面角,
∴二面角的余弦值为.
52.正多面体也称柏拉图立体,被喻为最有规律的立体结构,其所有面都只由一种正多边形构成的多面体(各面都是全等的正多边形,且每一个顶点所接的面数都一样,各相邻面所成二面角都相等).数学家已经证明世界上只存在五种柏拉图立体,即正四面体、正六面体、正八面体、正十二面体、正二十面体.已知一个正四面体和一个正八面体的棱长都是a(如图),把它们拼接起来,使它们一个表面重合,得到一个新多面体.
(1)求新多面体的体积;
(2)求二面角的余弦值;
(3)求新多面体为几面体?并证明.
【答案】(1);(2);(3)新多面体是七面体;证明见解析.
【分析】
(1)分别求得正四面体和正八面体的体积,由新多面体体积为原正四面体体积与正八面体体积之和求解;
(2)在正八面体中,取的中点为M,连结,易得为二面角的平面角,利用余弦定理求解;
(3)由(2)可知,正八面体任何相邻面构成的二面角余弦值均为,设此角为.再求得四面体相邻面所构成的二面角的余弦值为判断.
【详解】
(1)如图所示:,在正四面体中,分别取PT,QR的中点,连接QN,RN,NG,
则 ,
所以平面QNR,
所以正四面体的体积为 ,
如图所示,在正八面体中,连接AC交平面EFBH于点O,则平面EFBH,
所以 ,
所以正八面体的体积为,
因为新多面体体积为原正四面体体积与正八面体体积之和,
所以.
(2)如图,在正八面体中,取的中点为M,连结,易得为二面角的平面角.
易得,,
由余弦定理得.
(3)新多面体是七面体,证明如下:
由(2)可知,正八面体任何相邻面构成的二面角余弦值均为,设此角为.
在正四面体中,易得为二面角的平面角.
由余弦定理得,
即正四面体相邻面所构成的二面角的余弦值为,
所以,因此新多面体是七面体.
53.中国是风筝的故乡,南方称“鹞”,北方称“鸢”,如图,某种风筝的骨架模型是四棱锥,其中于,,,平面.
(1)求证:;
(2)试验表明,当时,风筝表现最好,求此时直线与平面所成角的正弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)利用平面可得,再利用即可;
(2)以为坐标原点,分别以,,为,,轴正方向,建立空间直角坐标系即可求出;或利用等体积法也可.
【详解】
(1)证明:∵平面,平面,
∴,又,
,平面,平面,
∴平面,
又平面.
∴.
(2)解:法一:如图,
以为坐标原点,分别以,,为,,轴正方向,建立空间直角坐标系,则,,,,
∴,,,
设为平面的法向量,
则,即,
令,则,
设直线与平面所成角为,
则.
法二:如图,
在中,由得,
在中,由得,
在中,由得.
在中,由得,
在中,由,
得,
,
设点到平面的距离为,
由,
得,
即,
设直线与平面所成的角为,
则.
54.在陕西汉中勉县的汉江河与定军山武侯坪一带,经常出土有铜、铁扎马钉等兵器文物.扎马钉(如题21图(1))是三国时蜀汉的著名政治家、军事家诸葛亮所发明的一种对付骑兵的武器,状若荆刺,故学名蒺藜,有铜、铁两种.扎马钉有四个锋利的尖爪,随手一掷,三尖撑地,一尖直立向上,推倒上尖,下尖又起,始终如此,使触者不能避其锋而被刺伤.即总有一个尖垂直向上,三尖对称支承于地.简化扎马钉的结构,如图(2),记组成该“钉”的四条等长的线段公共点为,钉尖为().
(Ⅰ)判断四面体的形状特征;
(Ⅱ)若某个出土的扎马钉因年代久远,有一尖爪受损,其长度仅剩其他尖爪长度的(即),如图(3),将,,置于地面,求与面所成角的正弦值.
【答案】(Ⅰ)该四面体的各个面都是全等的正三角形.;(Ⅱ).
【分析】
(Ⅰ)根据扎马钉总有一个尖垂直向上,可推出,从而可得答案;
(Ⅱ)为原点,以、所在直线为、轴,建立空间直角坐标系,利用空间向量可求出结果.
【详解】
(Ⅰ)点为四面体外接球的球心,即,且面,面,面,面,则空间四面体的每一条棱都相等,即;
所以该四面体的各个面都是全等的正三角形.
(Ⅱ)在四面体中,不妨令,,
在面内作点的射影,连接,
在等边中,为其外心,则,
在直角中,可得,
所以 ,解得,所以,
又因为面,且垂足为,
故以为原点,以、所在直线为、轴,建立空间直角坐标系,则 ,,,,,,
因为,即,则 ,
所以 ,,
设平面的一个法向量为,
则 ,即,令,得,
又 ,所以 ,
故与面所成角的正弦值为.
55.正多面体也称柏拉图立体,被誉为最有规律的立体结构,其所有面都只由一种正多边形构成的多面体(各面都是全等的正多边形,且每一个顶点所接的面数都一样,各相邻面所成二面角都相等).数学家已经证明世界上只存在五种柏拉图立体,即正四面体、正六面体、正八面体、正十二面体、正二十面体.已知一个正四面体和一个正八面体的棱长都是(如图),把它们拼接起来,使它们一个表面重合,得到一个新多面体.
(1)求新多面体的体积;
(2)求正八面体中二面角的余弦值;
(3)判断新多面体为几面体?(只需给出答案,无需证明)
【答案】(1);(2);(3)七面体.
【分析】
(1)分别取、的中点、,连接、、,证明出平面,计算出的面积,利用锥体的体积公式可求得正四面体的体积,利用锥体的体积公式可求得正八面体的体积,进而可得出新多面体的体积为正四面体和正八面体体积之积,即可得解;
(2)在正八面体中,取的中点为,连接,分析出为二面角的平面角,计算出三边边长,利用余弦定理可求得结果;
(3)计算出正四面体相邻面所构成的二面角与正八面体相邻面所构成的二面角互补,由此可得出结论.
【详解】
(1)分别取、的中点、,连接、、,如下图所示:
因为,为的中点,则且,
同理可知且,
,所以,平面,
为的中点,则,且,
,
所以正四面体的体积为;
如下图所示:
在正八面体中,连接交平面于点,则平面,
所以,,
所以正八面体的体积为,
因为新多面体体积为原正四面体体积与正八面体体积之和,
所以,新多面体的体积为;
(2)如图,在正八面体中,取的中点为,连接,
,为的中点,则,且,
同理可知,且,
所以,为二面角的平面角.
,
由余弦定理得,
故二面角的余弦值为;
(3)新多面体是七面体.
证明如下:由(2)可知,正八面体任何相邻面构成的二面角余弦值均为,设此角为.
在正四面体中,因为,,故为二面角的平面角.由余弦定理得,
即正四面体相邻面所构成的二面角的余弦值为,
所以,因此新多面体是七面体.)
56.如图,已知在四棱锥中,底面为等腰梯形,,,为棱上一点,与交于点,且,,,.
(1)证明:;
(2)是否存在点,使二面角的余弦值为?若存在,求出点位置,若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在;位置在靠近点的三等分点处.
【分析】
(1)根据几何关系得,进而得以平面,故;
(2)根据几何关系得,进而得平面,故以为原点,,,分别为,轴建立空间直角坐标系,利用坐标法求解即可.
【详解】
解:(1)证明:因为四边形为等腰梯形,且
所以为等腰直角三角形
因为,
所以,
因为,,
所以
所以
又因为平面,平面,
所以平面
因为平面
所以
(2)因为,,
所以,即
因为,平面,平面,
所以平面
如图,以为原点,,,分别为,轴建立空间直角坐标系,
由(1)知,
故,,,,,
,,
假设在棱上存在一点满足题意,设,.
所以
设平面的一个法向量为,
则,即,
令,解得,故
易得平面的一个法向量为
设二面角为,可知二面角为锐二面角
解得,
所以存在满足题意的点,位置在靠近点的三等分点处
57.如图,在三棱柱中点,在棱上,点F在棱CC1上,且点均不是棱的端点,平面且四边形与四边形的面积相等.
(1)求证:四边形是矩形;
(2)若,求平面与平面所成角的正弦值.
【答案】(1)证明见解析;(2)
【分析】
(1)由平面AEF,知平面AEF,求得,由四边形与四边形面积相等知,,则,故,结合,从而有四边形为矩形.
(2)证得平面,取BC的中点H,以G点为坐标原点,的方向分别为x,y,z轴建立空间直角坐标系,求得平面AEF和平面ABC的一个法向量,利用向量夹角求得二面角的正弦值.
【详解】
(1)在三棱柱中,,则由平面AEF,知平面AEF,
故,,,从而,
由四边形与四边形面积相等知,
又,则,故
结合,知四边形为平行四边形,又,
故四边形为矩形.
(2)取EF的中点G,联结AG,由(1)知,
且平面,则平面平面,
又平面平面,则平面,
取BC的中点H,以G点为坐标原点,的方向分别为x,y,z轴建立如图所示空间直角坐标系,
由知,为正三角形,故,
故,,,,,
设平面ABC的一个法向量为
则,故,
取,则,
因为平面AEF的一个法向量为
则
则二面角的余弦值为,故二面角的正弦值为
58.如图,在三棱台中,侧棱平面点在棱上,且
(1)证明:平面;
(2)当二面角的余弦值为,求的值.
【答案】(1)证明见解析;(2).
【分析】
(1)通过已知条件证明、,由此结合线面垂直的判定定理完成证明;
(2)建立合适空间直角坐标系,分别表示出平面、平面的一个法向量,然后表示出法向量夹角的余弦值,根据二面角的余弦值和法向量夹角的余弦值的关系求解出的值.
【详解】
(1)因为,所以,
又因为平面,平面,所以,
又,所以平面,所以,
又因为,,
所以,所以,
又,所以平面;
(2)以为坐标原点,分别为轴建立空间直角坐标系,如下图所示:
因为,
所以,
因为,所以,
设平面一个法向量为,设平面一个法向量为,
且,
因为,所以,令,所以,
又因为,所以,令,所以,
所以,
又因为二面角的余弦值为,
所以,所以解得(舍去),
综上可知:.
59.在直四棱柱中,底面ABCD为平行四边形,,点M在棱上,点N是BC的中点,且满足.
(1)证明:AM⊥平面;
(2)若M是的中点,求二面角的正弦值.
【答案】(1)证明见解析;(2)
【分析】
(1)由条件求得,结合,证得平面ACM,则,则,由条件知,平面;
(2)取的中点为E,则,,从而有平面,,为二面角的平面角,又M是的中点,根据线线关系求得侧棱长,从而求得,,在三角形中求得正弦值即可.
【详解】
(1)联结AC,由知,,即,
由在直四棱柱中,平面ABCD,则
又,则平面ACM,又平面ACM,
则,又,则,由条件知,
且,故平面;
(2)由(1)知为等腰直角三角形,取的中点为E,
联结,则,
又在直四棱柱中,平面,则,
从而有平面,
过E点作的垂线,垂直为F,联结,
此时由知,平面,
则,为二面角的平面角,
又M是的中点,取的中点为G,易知,由题知,设,
则,,
则
则在中,,即,
解得
则在中,,,
则,
故二面角的正弦值为.
60.在四棱锥中,四边形是边长为4的菱形,,.
(1)证明:平面;
(2)如图,取的中点为,在线段上取一点使得,求二面角的大小.
【答案】(1)证明见解析;(2).
【分析】
(1)利用勾股定理逆定理计算证明,,进而利用线面垂直判定定理证得平面,从而,在计算证得,得到平面,从而,证得平面;
(2)以,,所在的直线为,,轴,建立空间直角坐标系,利用空间向量计算求解.
【详解】
(1)因为,,所以,所以,
又因为为平行四边形,所以,,
因为,,,所以,所以,
因为,所以平面,所以,
因为,,,所以,所以,
因为,所以平面,所以,
因为,所以平面.
(2)由(1)知,,,两两垂直,分别以,,所在的直线为,,轴,建立如图所示的空间直角坐标系,
在三角形中,,
则,,,,,,
所以,
因为,,,
,
设平面的一个法向量为,
则,即,
令,得,,于是取,
又由(1)知,底面为正方形,所以,
因为平面,所以,
因为,所以平面,
所以是平面的一个法向量,
设二面角的大小为,则,
所以二面角的大小为.
61.如图,在底面是菱形的四棱柱中,,,点在上.
(1)求证:平面;
(2)当为线段的中点时,求点到平面的距离.
【答案】(1)证明见解析;(2).
【分析】
(1)由得,由得可得答案;
(2)当时得点为的中点时,可得平面,转化为求点到平面的距离,设的中点为,则,得平面,利用可求得,利用可得答案.
【详解】
(1)证明:因为底面为菱形,,所以,由知
,由知,
又因为,所以平面.
(2)当时,平面.证明如下:
连结交于,当时,即点为的中点时,连结,
则,平面,平面,所以平面,
所以直线与平面之间的距离等于点到平面的距离,
因为点为的中点,可转化为到平面的距离,,
设的中点为,连结,则,
所以平面,且,可求得,
所以,
又,,,,
所以(表示点到平面的距离),,
所以直线与平面之间的距离为.
62.已知四棱锥的底面是菱形,对角线、交于点,,,底面,设点满足.
(1)若三棱锥体积是,求的值;
(2)若直线与平面所成角的正弦值是,求的值.
【答案】(1);(2).
【分析】
(1)由题意知,、、两两垂直,建立空间直角坐标系,设,由 ,求得M的坐标,过作于,于,再由求解;
(2)由(1)知,求得平面的一个法向量为,设直线与平面所成的角为,然后由求解.
【详解】
(1)因为四边形是菱形,所以,
因为底面,所以、,
所以、、两两垂直,
建立如图所示的空间直角坐标系,
设,,,
因为,所以,
于是,所以,
过作于,过作于,
所以
,
解得.
(2)由(1)知,,,
设平面的一个法向量为,
,
令,,
设直线与平面所成的角为,
所以,
解得或(舍去).
63.光学器件在制作的过程中往往需要进行切割,现生产一种光学器件,有一道工序为将原材料切割为两个部分,然后在截面上涂抹一种光触媒化学试剂,加入纳米纤维导管后粘合.在如图所示的原材料器件直三棱柱ABC﹣A'B'C'中,AB⊥AC,AB=AC=AA'=a,现经过AB作与底面ABC所成角为θ的截面,且截面与B'C',A'C'分别交于不同的两点E,F.
(1)试求截面面积S随θ变化的函数关系式S(θ);
(2)当E和F分别为和的中点时,需要在线段AF上寻找一个点Q,用纳米纤维导管连接EQ,使得EQ与AB'所在直线的夹角最小,试求出纤维导管EQ的长.
【答案】(1) ;(2) 纤维导管EQ的长为.
【分析】
(1)利用直棱柱的结果特征确定截面的形状,然后利用相关量的位置关系和数量关系求解S(θ)的解析式即可;
(2)建立适当的空间直角坐标系,得到相关的坐标,设,根据向量的夹角公式并利用换元法求得满足题目要求时点Q的坐标,进而求出BQ的长.
【详解】
解:(1)该几何体是直棱柱,故平面平面,
而平面平面,,故平面,
因为过的截面与平面的交线都与垂直,
又平面平面,平面平面ABEF=EF,所以,
所以截面ABEF为直角梯形,且截面与底面的平面角为,
则,,
过F作于点D,则,,
所以梯形ABEF面积
,
所以;
(2)以A为坐标原点,直线AC、AB、分别为x,y,z轴,
建立如图空间直角坐标系,
则,,
而E和F分别为和的中点,
故,.
设,,
则,则,
所以.设EQ与的夹角为,
则
,设,则
则,
当且仅当时,即时,取得最大值,为.
因为余弦函数在上单调递减,
所以当时直线EQ与AB'的夹角最小,此时,,
所以,
所以纤维导管EQ的长为.
64.如图,四棱锥P﹣ABCD的底面ABCD为菱形,∠ABC=60°,PA⊥平面ABCD,且E,M分别为BC,PD的中点,点F为棱PC上一动点.
(1)证明:平面AEF⊥平面PAD.
(2)若AB=PA,在线段PC上是否存在一点F,使得二面角F﹣AE﹣M的正弦值为?若存在,试确定F的位置;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在点F,当F为线段PC的中点或F为线段PC的靠近点C的五等分点,能够使得得二面角F﹣AE﹣M的正弦值为.
【分析】
(1)连结AC,证明AE⊥BC和PA⊥AE,得到AE⊥面,再利用面面垂直的判定定理可以证明面AEF⊥平面PAD;
(2)以A为原点,分别为x、y、z轴正方向建立空间直角坐标系,用向量法求解即可.
【详解】
(1)连结AC,
因为底面ABCD为菱形,∠ABC=60°,所以三角形ABC为等边三角形,
因为E为BC的中点,所以AE⊥BC.
又AD∥BC,所以AE⊥AD.
因为PA⊥平面ABCD,所以PA⊥AE.
因为,所以AE⊥面.
因为面,所以面AEF⊥平面PAD.
(2)
以A为原点,分别为x、y、z轴正方向建立空间直角坐标系,不妨设,则:
所以
设,则
设平面AEM的一个法向量为,则,即,
不妨设y=1,则.
同理可求平面AEF的一个法向量为.
假设存在点F符合题意,即存在点F,使得二面角F﹣AE﹣M的正弦值为,
所以二面角F﹣AE﹣M的余弦值为,
所以,解得:或,
故存在点F,当F为线段PC的中点或F为线段PC的靠近点C的五等分点,能够使得得二面角F﹣AE﹣M的正弦值为.
65.如图,三棱柱中,,,.
(1)求证:为等腰三角形;
(2)若,,点在线段上,设,若二面角的余弦值为,求的值.
【答案】(1)证明见解析;(2).
【分析】
(1)取的中点,连接,,,可证,,即可得到平面,根据线面垂直的性质得到,即可得证;
(2)设,以为原点,,,分别为,,轴建立空间直角坐标系,设,表示出平面的法向量,求出平面的法向量,根据二面角的余弦值为,得到方程,解得即可;
【详解】
(1)如图,取的中点,连接,,,
∵,∴;
而,∴为等边三角形,∴.
又∵,,∴,∴,
又,平面,∴平面,
又平面,∴,
∵为中点,∴,即为等腰三角形.
(2)设,则,
∵,故,∴,
又,,∴,
以为原点,,,分别为,,轴建立空间直角坐标系,
则,,.
设,则,,
设平面的法向量为,则由,,
得,取,
易知平面的法向量为,
则,解得(舍去).
66.如图,四棱锥中,底面为菱形,,,平面,.
(1)点E在线段PC上,,点F在线段PD上,,求证:平面;
(2)设M是直线AC上一点,求CM的长,使得MP与平面PCD所成角为.
【答案】(1)证明见解析;(2)或
【分析】
方法一:(1)根据题意,在中,由余弦定理得,进而得,在中,由余弦定理,进而在中,由余弦定理得,故,进而平面;
(2)设,点M到平面的距离为,由得,进而由得,解方程即可得答案.
方法二:以所在直线为x轴,以所在直线为z轴建立空间直线坐标系利用坐标法证明.
【详解】
法1:(1)因为平面ABCD,,
所以,
因为底面为菱形,,
所以,
因为,所以,
所以在中,由余弦定理得,
所以,即,
所以在中,由余弦定理
所以在中,由余弦定理得,
因为,所以
又,所以平面
(2)设,点M到平面的距离为,则由,得,
所以,即
解得或
从而得M点与A点重合或在的反向延长线上,则得或
法2:(1)以所在直线为x轴,以所在直线为z轴建立空间直线坐标系
则
,
所以
,
所以
又,所以平面
(2),
设是平面的一个法向量,则,得
,设,
所以,
因为MP与平面PCD所成角为,
所以
解得或
从而得M点与A点重合或在的反向延长线上,则得或
67.如图,在四棱锥中,底面为正方形,侧棱底面,,,为的中点,点在棱上,且.
(1)求直线与直线所成角的余弦值;
(2)当直线与平面所成的角最大时,求此时的值.
【答案】(1);(2).
【分析】
(1)以为坐标原点,,,所在直线为,,轴,建立空间直角坐标系,利用向量法能求出与所成角的余弦值.
(2)求出平面的法向量,利用向量法能求出的值.
【详解】
(1)如图,以为坐标原点,,,所在直线为,,轴,建立空间直角坐标系,
则,,,,
,,
∴,
∴与所成角的余弦值为.
(2)点在棱上,且,∴,
∴,,
又,.
设为平面的法向量,
则,取,得,
设直线与平面所成的角为,
则
,
令,则,
∴,
当,即时,有最小值,此时取得最大值为,
即与平面所成的角最大,此时,即的值为.
68.如图,在四棱锥中,四边形为直角梯形,,,且,,,M为的中点,平面平面,直线与平面所成角的正切值为.
(1)求四棱锥的体积;
(2)在棱上(不含端点)是否存在一点Q,使得二面角的余弦值为?若存在,请确定点Q的位置;若不存在,请说明理由.
【答案】(1);(2)存在,为的中点,理由见解析.
【分析】
(1)先根据面面垂直,线面垂直的性质定理以及线面垂直的判定定理得到为四棱锥的高,再根据直线与平面所成角的正切值为,即可求出,最后根据椎体的体积公式即可求解;(2)先假设存在,设,再根据二面角的余弦值为以及二面角的向量求法即可判断是否存在点.
【详解】
解:(1),M为的中点,
,
又平面平面,
平面,
即,
又,
平面,
故为四棱锥的高,
为直线与平面所成角,
又,
即,
四棱锥的体积为;
(2)假设存在点,建立如图所示的空间直角坐标系,
设,,
则,
则,,,
设平面和平面的法向量分别为,,
则,令,则,
,令,
则,
二面角的余弦值为,
化简得:,
又,
解得:,
即在棱上(不含端点)存在的中点Q,使得二面角的余弦值为.
69.已知四棱锥中,底面是平行四边形,,分别是的中点,.
(1)求证:平面;
(2)若,求二面角的余弦值.
【答案】(1)证明见解析;(2).
【分析】
(1)若要证明线面垂直,只要证明该直线垂直于平面内的两条相交直线,结合图像利用线面关系即可得解;
(2)建立空间直角坐标系,利用空间向量法,求出各个面的法向量,利用向量的夹角公式,即可得解.
【详解】
连接,
因为是平行四边形的的中点,
所以
又,所以,所以
从而.
因为,所以,所以
作BP的中点M,连接DM,AM
所以,DM⊥BP,AM⊥BP,又
故BP⊥平面ADM,又 平面,所以BP⊥AD.
又面面且
所以平面;
(2)设,则 ,
在中, ①,
在中,,②
联立①②得:,于是,即.
建立如图所示的空间直角坐标系,得
故,设是平面BPC的法向量,
所以,
取得.又AP⊥AD,AP⊥AB,AD∩AB=A,所以AP⊥平面ABCD,
平面 , 所以AP⊥BD
又BD⊥AC,AC∩AP=A,所以BD⊥平面APC,即是平面APC的一个法向量.
所以
所以二面角的余弦值为.
70.如图,矩形中,,将其沿翻折,使点到达点的位置,且二面角为直二面角.
(1)求证:平面平面;
(2)设是的中点,二面角的平面角的大小为,当时,求的取值范围.
【答案】(1)证明见解析;(2).
【分析】
(1)由直二面角证得,,进而证得平面即可得证;
(2) 作平面,射线EB,EA,Ez分别为x,y,z轴非负半轴建立空间直角坐标系,借助空间向量建立函数关系即可作答.
【详解】
(1)因二面角为直二面角,即平面平面,又,
平面平面,则平面,
即,而,,于是平面,平面,
所以平面平面;
(2)过E作平面,由(1)知,以为原点,射线EB,EA,Ez分别为x,y,z轴非负半轴建立空间直角坐标系,如图,
令,则,,,,,
,,,
设平面的法向量为,则,即
取,则,
设平面的法向量为,则,即,
取,则,由图可知二面角为锐二面角,
从而有,而,
所以.
(高级)70-100题
71.如图,在四棱锥中,底面是正方形,侧面底面,
,分别为中点,.
(1)求证:平面;
(2)求二面角的余弦值;
(3)在棱上是否存在一点,使平面?若存在,指出点的位置;若不存在,说明理由.
【答案】(1)证明见解析;(2);(3)不存在;理由见解析.
【分析】
(1)作的中点,连接,先利用面面平行的判定定理,证明出平面平面,进而根据面面平行的性质证明出平面;
(2)作垂直于,作,连接,作中点,连接,先证出为二面角的平面角,进而求得和,最后在直角三角形中求得;
(3)先假设存在点,建立空间直角坐标系,求得平面的一个法向量,表示出和,根据向量共线的性质建立等式对求解.
【详解】
(1)作的中点,连接,
∵在中,为中点,
∴,
∵平面,平面,
∴平面,
同理可证明平面,
∵平面,平面,,
∴平面平面,
∵平面,
∴平面;
(2)作垂直于,作,连接,作中点,连接,
∵,
∴,
∵,
∴,
∵为中点,
∴,,
∵侧面底面,
∴底面,
∵,
∴,
∴为二面角的平面角,
∵,
∴∽,
∴,,
∴
∴,
∴,
即二面角的余弦值为;
(3)不存在.
假设存在,连接,交于点,为平面和平面的交线,
以为原点,分别为轴建立空间直角坐标系,
则(1,0,0),(1,2,0),(﹣1,2,0),(﹣1,0,0),
,,(0,1,0),
设,则,
设平面的一个法向量是,
∵,
即,令,则,
∵因为平面,
∴,
∴,,,
∵,共线,,,
∴,
∴,无解,
故在棱上不存在一点,使得平面.
72.请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①;②;③点在平面的射影在直线上.如图,平面五边形中,是边长为的等边三角形,,,,将沿翻折成四棱锥,是棱上的动点(端点除外),分别是的中点,且___________.
(1)求证:;
(2)当与平面所成角最大时,求平面与平面所成的锐二面角的余弦值.
注:如果选择多个条件分别解答,按第一个解答计分.
【答案】条件选择见解析;(1)证明见解析;(2).
【分析】
(1)取的中点分别为,连接.
选择①:根据,,得到,进而得到平面,易得平面平面,从而得到平面即可.
选择②:连接,易得,进而得到,进而得到平面,易得平面平面,从而得到平面即可.
选择③:根据点在平面的射影在直线上,得到平面平面,进而得到平面,则,进而得到平面,易得平面平面,从而得到平面即可.
(2)连接,由平面,得到即为与平面所成的角,由,得到为中点时,最小,然后建立空间直角坐标系,取得平面的一个法向量为,以及平面的一个法向量为求解.
【详解】
(1)如图所示:
取的中点分别为,连接.
选择①:
因为,,
所以,即.
又,,
所以平面.
因为分别为的中点,
所以,且平面,平面,
所以平面.
同理可得:平面.
因为,
所以平面平面,…
所以平面.
又平面,
所以.
选择②:
连接,则,,
因为,
所以.
又,,
所以平面.
因为分别为的中点,
所以,且平面,平面,
所以平面.
同理可得:平面.
因为,
所以平面平面,
所以平面.
又平面,
所以.
选择③:
因为点在平面的射影在直线上,
所以平面平面.
因为平面平面,平面,,
所以平面,
所以.
又,,
所以平面.
因为分别为的中点,
所以,且平面,平面,
所以平面.…
同理可得:平面.
因为,
所以平面平面,
所以平面.
又平面,
所以.
(2)连接,由(1)可知:平面,
所以即为与平面所成的角.
因为,所以当最小时,最大,
所以当,即为中点,最小.
以点为坐标原点,以为轴,为轴,为轴,建立如图所示的空间直角坐标系,
则.
所以,.
设平面的一个法向量为,
则,令,得.
由题意可知:平面的一个法向量为,
所以,
所以平面与平面所成的锐二面角的余弦值为.
73.蜂房是自然界最神奇的“建筑”之一,如图1所示.蜂房结构是由正六棱柱截去三个相等的三棱锥,,,再分别以,,为轴将,,分别向上翻转,使,,三点重合为点所围成的曲顶多面体(下底面开口),如图2所示.蜂房曲顶空间的弯曲度可用曲率来刻画,定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和,而每一顶点的曲率规定等于减去蜂房多面体在该点的各个面角之和(多面体的面角是多面体的面的内角,用弧度制表示).
(1)求蜂房曲顶空间的弯曲度;
(2)若正六棱柱的侧面积一定,当蜂房表面积最小时,求其顶点的曲率的余弦值.
【答案】(1);(2);
【分析】
(1)根据蜂房曲顶空间的弯曲度的定义进行求解即可;(2)根据图形结构,设,接着将蜂房表面积表示成关于的函数,求导判断函数取最小值时的值,进而求得的大小,最后求解顶点的曲率的余弦值即可.
【详解】
(1)蜂房曲顶空间的弯曲度为顶端三个菱形的7个顶点的曲率之和,根据定义其度量值等于减去三个菱形的内角和,再减去6个直角梯形中的两个非直角内角和,
即蜂房曲顶空间的弯曲度为.
(2)设底面正六边形的边长为1,
如图所示,连接AC,SH,则,
设点在上底面ABCDEF的射影为O,则,
令,则,
菱形SAHC的面积,
的面积为,
令正六棱柱的侧面积为定值时,
蜂房的表面积为,
,令得到,
经研究函数的单调性,
得到函数在处取得极小值,
此时,
在中,令,
由余弦定理得,
顶点的曲率为,
其余弦值为.
74.2022年北京冬奥会标志性场馆——国家速滑馆的设计理念来源于一个冰和速度结合的创意,沿着外墙面由低到高盘旋而成的“冰丝带”,就像速度滑冰运动员高速滑动时留下的一圈圈风驰电掣的轨迹,冰上划痕成丝带,22条“冰丝带”又象征北京2022年冬奥会.其中“冰丝带”呈现出圆形平面、椭圆形平面、马鞍形双曲面三种造型,这种造型富有动感,体现了冰上运动的速度和激情这三种造型取自于球、椭球、椭圆柱等空间几何体,其设计参数包括曲率、挠率、面积体积等对几何图形的面积、体积计算方法的研究在中国数学史上有过辉煌的成就,如《九章算术》中记录了数学家刘徽提出利用牟合方盖的体积来推导球的体积公式,但由于不能计算牟合方盖的体积并没有得出球的体积计算公式直到200年以后数学家祖冲之、祖眶父子在《缀术》提出祖暅原理:“幂势既同,则积不容异”,才利用牟合方盖的体积推导出球的体积公式原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.
(Ⅰ)利用祖暅原理推导半径为的球的体积公式时,可以构造如图②所示的几何体,几何体的底面半径和高都为,其底面和半球体的底面同在平面内.设与平面平行且距离为的平面截两个几何体得到两个截面,请在图②中用阴影画出与图①中阴影截面面积相等的图形并给出证明;
(Ⅱ)现将椭圆所围成的椭圆面分别绕其长轴、短轴旋转一周后得两个不同的椭球,(如图),类比(Ⅰ)中的方法,探究椭球的体积公式,并写出椭球,的体积之比.
【答案】(Ⅰ)答案见解析;(Ⅱ),体积之比为.
【分析】
(Ⅰ)由题意,直接画出阴影即可,然后分别求出图①中圆的面积及图②中圆环的面积即可证明;
(Ⅱ)类比(Ⅰ)可知,椭圆的长半轴为,短半轴为,构造一个底面半径为,高为的圆柱,把半椭球与圆柱放在同一个平面上,在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,即挖去的圆锥底面半径为,高为,证明截面面积相等,由祖暅原理求出出椭球的体积,同理求出椭球的体积,作比得出答案.
【详解】
(Ⅰ)由图可知,图①几何体的为半径为的半球,图②几何体为底面半径和高都为的圆柱中挖掉了一个圆锥,与图①截面面积相等的图形是圆环(如阴影部分)
证明如下:
在图①中,设截面圆的圆心为,易得截面圆的面积为,
在图②中,截面截圆锥得到的小圆的半径为,所以,圆环的面积为,所以,截得的截面的面积相等
(Ⅱ)类比(Ⅰ)可知,椭圆的长半轴为,短半轴为,构造一个底面半径为,高为的圆柱,把半椭球与圆柱放在同一个平面上(如图),在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,即挖去的圆锥底面半径为,高为;
在半椭球截面圆的面积,
在圆柱内圆环的面积为
∴距离平面为的平面截取两个几何体的平面面积相等,
根据祖暅原理得出椭球的体积为:
,
同理:椭球的体积为
所以,两个椭球,的体积之比为.
75.如图,已知边长为2的正方形材料,截去如图所示的阴影部分后,可焊接成一个正四棱锥的封闭容器.设.
(1)用表示此容器的体积;
(2)当此容器的体积最大时,求的值.
【答案】(1),;(2).
【分析】
(1)取的中点,连接,连接交于,根据题意可求出正方形的边长,进而求出底面积和高,即可求出体积;
(2)令,求出的导数,利用导数判断其单调性,从而可求出其最大值,即得解.
【详解】
(1)取的中点,连接,连接交于,如图.
由题意知,在直角三角形中,.
在直角三角形中,,
所以,所以.
因为,所以.
从而,正四棱锥高
,
所以正四棱锥的体积
,.
(2)令,,则,
.
令,得.
+
0
-
↗
极大值
↘
所以在单调递增,在单调递减,
所以在时取到最大值,此时.
76.如图,在四面体中,,平面与平面垂直且.
(1)若,证明:;
(2)若,当与面积之和最大时,求二面角的余弦值.
【答案】(1)见详解;(2).
【分析】
(1)作于点,连接,根据线面垂直的判定定理,以及面面垂直的性质,得到;推出,得到,即可证明结论成立;
(2)先由(1)知:,设,作于点,用表示出,求出其最大时,作交于点,于是即是二面角的平面角,根据题中数据,计算的余弦值,即可得出结果.
【详解】
(1)证:作于点,连接,
由平面与平面垂直,知平面.
则;
又,,平面,平面,
所以平面,所以;
于是,又,
所以,故;
(2)同(1)可知:,
设,作于点,由得:,,,,
所以,
令,
由柯西不等式可得:,
当且仅当,即时,等号成立;
所以,
当且仅当,即时,等号成立;
即与面积之和最大时,,即,
所以,,,,
作交于点,于是即是二面角的平面角,
又,
所以,
则,则,
,
所以,
故.
77.某人设计了一个工作台,如图所示,工作台的下半部分是个正四棱柱ABCD﹣A1B1C1D1,其底面边长为4,高为1,工作台的上半部分是一个底面半径为的圆柱体的四分之一.
(1)当圆弧E2F2(包括端点)上的点P与B1的最短距离为5时,证明:DB1⊥平面D2EF.
(2)若D1D2=3.当点P在圆弧E2E2(包括端点)上移动时,求二面角P﹣A1C1﹣B1的正切值的取值范围.
【答案】(1)见解析,(2)
【分析】
(1)以为原点,以的方向分别为轴,轴,轴的正方向建立空间直角坐标系,可得,从而可证DB1⊥平面D2EF;
(2)设,则,所以,求出平面的法向量,而平面的一个法向量,设二面角的大小为,则先求出,从而可得,再由可得的范围.
【详解】
(1)证明:作平面于,则在圆弧上,
因为,所以当取最小值时,最小,
由圆的对称性可知,的最小值为,
所以,
如图,以为原点,以的方向分别为轴,轴,
轴的正方向建立空间直角坐标系,
则,
,
因为,
所以,
因为平面,平面,,
所以DB1⊥平面D2EF,
(2)解:若D1D2=3,由(1)知,
设,因为,
设
所以,
,
设平面的法向量为,
则,
令,则,
取平面的一个法向量,
设二面角的大小为,显然是钝角,
则,
,
则,
所以二面角的正切值的取值范围为.
78.平面凸六边形的边长相等,其中为矩形,.将,分别沿,折至,,且均在同侧与平面垂直,连接,如图所示,E,G分别是,的中点.
(1)求证:多面体为直三棱柱;
(2)求二面角平面角的余弦值.
【答案】(1)详见解析;(2).
【分析】
(1) 取中点F,连接,,再证明四边形为平行四边形,进而根据平行四边形的性质证得平面平面,同时证得侧棱且互相相等,再证明平面即可.
(2) 过F作交于点D,连接,根据线面垂直的性质可得为二面角的平面角以及二面角的平面角为,进而根据三角形中的边长关系结合勾股定理求解即可.
【详解】
(1)证明:取中点F,连接,.
∵F为中点,,又面平面,
且面平面,
∴平面.
同理可证平面,,而,故四边形为平行四边形,从而,,
又,,,故且,因此四边形为平面四边形,则,
而平面,平面,故平面;
由题设显然有平面,而,故平面平面,
又四边形,为平行四边形,则,从而四边形为平行四边形,而平面,因此多面体为直三棱柱;
(2)过F作交于点D,连接.
由(1)平面知,而,,因此平面,则 ,
故为二面角的平面角,
而平面,平面,则平面平面,
因此二面角的平面角为,
设,则,,,
从而,
故,
则
79.如图,是圆的直径,点是圆上异于的点,直线平面,分别是的中点.
(1)记平面与平面的交线为,试判断直线与平面的位置关系,并加以证明;
(2)设(1)中的直线与圆的另一个交点为,且点满足.记直线与平面所成的角为,异面直线与所成的角为,二面角的大小为,求证:.
【答案】(1)见解析;(2)见解析;
【分析】
(1)直线平面PAC. 连接EF,利用三角形的中位线定理可得,EFAC,再利用线面平行的判定定理即可得到平面ABC,再由线面平行的性质定理可得EF,再利用线面平行的判定定理即可证明直线平面PAC;
(2)以点为原点,向量所在直线分别为轴,建立空间直角坐标系,利用平面的法向量和直线的方向向量可得出线面角,两个直线的方向向量可得出线线角,两个平面的法向量的夹角即可得出二面角,从面即可证明结论.
【详解】
(1)直线平面,证明如下:
连接EF,因为分别是的中点,所以EFAC,
又平面,且平面,
所以平面,
而平面,且平面平面,
所以EF,
又因为平面,平面,
所以直线平面
(2) 由题意得:,作,且,
连接,由(1)可知交线即为直线,
以点为原点,向量所在直线分别为轴,建立空间直角坐标系( 如图):
设,则有
所以:,
又取平面的一个法向量为,
,
设平面的法向量为,
所以由可得,令,
则,
,
,
故,
即
80.已知,图中直棱柱的底面是菱形,其中.又点分别在棱上运动,且满足:,.
(1)求证:四点共面,并证明∥平面.
(2)是否存在点使得二面角的余弦值为?如果存在,求出的长;如果不存在,请说明理由.
【答案】(1)见解析(2)不存在点使之成立.见解析
【分析】
(1) 在线段上分别取点,使得,进而得到与即可.
(2) 以为原点,分别以,及过且与平行的直线为轴建立空间直角坐标系,再求解平面的法向量与平面的法向量,再设,,再根据二面角的计算方法分析是否存在使得二面角为的余弦值为即可.
【详解】
解:(1)证法1:在线段上分别取点,使得,易知四边形是平行四边形,所以,联结,
则,且
所以四边形为矩形,故,同理,
且,故四边形是平行四边形,所以,所以
故四点共面
又,平面,平面,
所以平面.
证法2:因为直棱柱的底面是菱形,∴,底面,设交点为,以为原点,分别以,及过且与平行的直线为轴建立空间直角坐标系.则有,,,,设,,则,,,,,,所以,故四点共面.又,平面,平面,所以平面.
(2)平面中向量,,设平面的一个法向量为,则,可得其一个法向量为.
平面中,,,设平面的一个法向量为
,则,所以取其一个法向量.
若,则,
即有,,解得,故不存在点使之成立.
81.如图1,与是处在同-个平面内的两个全等的直角三角形,,,连接是边上一点,过作,交于点,沿将向上翻折,得到如图2所示的六面体
(1)求证:
(2)设若平面底面,若平面与平面所成角的余弦值为,求的值;
(3)若平面底面,求六面体的体积的最大值.
【答案】(1)证明见解析(2)(3)
【分析】
根据折叠图形, ,由线面垂直的判定定理可得平面,再根据平面,得到.
(2)根据,以为坐标原点,为轴建立空间直角坐标系,根据,可知,,表示相应点的坐标,分别求得平面与平面的法向量,代入求解.
设所求几何体的体积为,设为高,则,表示梯形BEFD和 ABD的面积由,再利用导数求最值.
【详解】
(1)证明:不妨设与的交点为与的交点为
由题知,,则有
又,则有
由折叠可知所以可证
由平面平面,
则有平面
又因为平面,
所以....
(2)解:依题意,有平面平面,
又平面,
则有平面,,又由题意知,
如图所示:
以为坐标原点,为轴建立如图所示的空间直角坐标系
由题意知
由可知,
则
则有,
,
设平面与平面的法向量分别为
则有
则
所以
因为,解得
设所求几何体的体积为,设,
则,
当时,,当时,
在是增函数,在上是减函数
当时,有最大值,
即
六面体的体积的最大值是
82.设三棱锥的每个顶点都在球的球面上,是面积为的等边三角形,,,且平面平面.
(1)确定的位置(需要说明理由),并证明:平面平面.
(2)与侧面平行的平面与棱,,分别交于,,,求四面体的体积的最大值.
【答案】(1)在上,理由见解析,证明见解析,(2)
【分析】
(1)取的中点,连接,可证在线段上,且平面,从而得到平面平面.
(2)设,可证,利用导数可求体积的最大值.
【详解】
(1)证明:取的中点,连接,取点为的三等分点且,
连接.
因为,所以.
又平面平面,平面平面,平面,
所以平面.
因为平面,故.
因为为等腰直角三角形,为的中点,故,
因为,,
故,故,同理,
因为是等边三角形,故为的中心,故,
故为三棱锥的外接球的球心,
故与重合即在线段上且.
因为在上,所以平面,
又平面,所以平面平面.
(2)由题意得,解得,
因为为等腰直角三角形,为的中点,故,
而平面平面,平面平面,
平面,故平面,故为点到平面的距离.
在等腰直角三角形中,即到平面的距离.
设,到平面的距离为.
因为平面平面,平面平面,平面平面,
故,同理,因为方向相同,故,
同理,
所以,则的面积为.
又,所以到平面的距离为,
所以四面体的体积.
设,,
当时,;当时,.
所以在为增函数,在为减函数,
所以,
即四面体的体积的最大值为.
83.如图,在三棱柱中,平面,是的中点,,,.
(Ⅰ)求证:平面;
(Ⅱ)求平面与平面所成锐二面角的平面角的余弦值.
【答案】(Ⅰ)证明见解析,(Ⅱ)
【分析】
(Ⅰ)连结交于点,连结,可知,根据线面平行的判定定理,证明即可.
(Ⅱ)法一: 由,,可知,即,根据平面,可知平面,即,,以为原点,,,所在直线分别为,, 轴,建立空间直角坐标系,求各点坐标,计算平面的法向量为,平面的法向量为,根据,求解即可. 法二:延长、交于,连接,过作于,过作于,连接,则平面,,又,所以平面,为平面与平面所成锐二面角的平面角. 由,,,计算
,,利用,求解,即可.
【详解】
(Ⅰ)证明:连结交于点,连结.
则为中点,为中位线.
所以.
又平面,平面.
所以平面.
(Ⅱ)法一:因为,是的中点,所以.
又因为,所以,则
即,所以.
又因为平面,所以建立如图所示空间直角坐标系,则,,,,.
平面的法向量为.
设平面的法向量为,则由,,得
令,则,.
所以平面与平面所成的锐二面角的余弦值为.
法二:延长、交于,连接,过作于,
过作于,连接,
则平面,,又,所以平面,
为平面与平面所成锐二面角的平面角.
中,,所以高为中线,,,
∵,∴,∴,
中,,
,∴
中,,,
所以平面与平面所成锐二面角的平面角的余弦值为.
84.如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,为底面圆的内接正三角形,且边长为在母线上,且.
(1)求证:平面平面;
(2)设线段上动点为,求直线与平面所成角的正弦值的最大值.
【答案】
(1)证明见解析
(2)1
【分析】
(1)设交于点连接,由,
并结合可证得平面由此证得,
再利用三角形相似证得从而证得平面进而证得平面平面;
(2)建立空间直角坐标系,设,
通过向量和平面的法向量建立直线与平面所成角的正弦值的关系式,并利用基本不等式,即可求最值.
(1)
证明:如图,设交于点连接,
易知,
又平面平面,
又平面.又是底面圆的内接正三角形,
由,可得,.又,,
即.又,,
,即.又平面,,
平面.又平面,平面平面.
(2)
易知.以点为坐标原点,所在直线分别为轴、轴、轴,建立如图所示的空间直角坐标系,
则,
设平面的法向量为,
则,即,令,则.设,
可得.
设直线与平面所成的角为,则.
令,,则
,当且仅当时,等号成立,
当时,有最大值,
于是当时,有最大值为,
的最大值为,
故直线与平面所成角的正弦值的最大值为.
85.如图,三棱柱的底面是边长为4的正三角形,侧面底面,且侧面为菱形,.
(1)求二面角所成角的正弦值.
(2)分别是棱,的中点,又.求经过三点的平面截三棱柱的截面的周长.
【答案】(1);(2).
【分析】
(1)为的中点,连接,以为坐标原点,分别以的方向为轴,轴,z轴的正方向,建立如图所示的空间直角坐标系.求出平面的一个法向量,平面的一个法向量.利用空间向量的数量积求解二面角所成角的正弦值即可;
(2)连接,经过三点的平面截三棱柱的截面即为平面,利用余弦定理,结合求解三角形推出截面的周长.
【详解】
(1)为的中点,连接,侧面为菱形,,
△为正三角形,,
侧面底面,侧面底面,侧面,
底面,
底面为正三角形,为的中点,,
以为坐标原点,分别以,,的方向为轴,轴,轴的正方向,建立如图所示的空间直角坐标系.
底面是边长为4的正三角形,
,0,,,,,,,2,,,
,,,
设平面的一个法向量为,
由得,令,得,
,
又易知为平面的一个法向量.
.
所以二面角所成角的正弦值为.
(2)连接,,,,分别是棱,的中点,,
又因为,,经过,,三点的平面截三棱柱的截面即为平面,
其中,在△中,因为三棱柱的底面是边长为4的正三角形,
侧面为菱形,,
由余弦定理得,
取的中点,连接,四边形为平行四边形,,
又因为侧面为菱形,,△为两个全等的等边三角形,
连接,,又因为,,
又因为侧面底面,且侧面底面,平面,
又平面,,
又因为,,
即,所以截面的周长为:.
86.如图,在三棱台中,底面是边长为2的正三角形,侧面为等腰梯形,且,为的中点.
(1)证明:;
(2)记二面角的大小为,时,求直线与平面所成角的正弦值的取值范围.
【答案】(1)证明见解析;(2).
【分析】
(1)通过证明,得出平面,即可由线面垂直的性质得出;
(2)以为坐标原点建立空间直角坐标系,可得为二面角的平面角,,求出平面的法向量和,利用向量关系可表示出直线与平面所成角的正弦值,即可根据范围求出.
【详解】
(1)证明:如图,作的中点,连接,,
在等腰梯形中,,为,的中点,
∴,
在正中,为的中点,
∴,
∵,,,,平面,
∴平面,
又平面,∴.
(2)解:∵平面,
在平面内作,以为坐标原点,以,,,分别为,,,轴正向,如图建立空间直角坐标系,
∵,,∴为二面角的平面角,即,
,,,,,,
设平面的法向量为,,,
则有,即,
则可取,又,
设直线与平面所成角为,
∴,
∵,∴,
∴.
87.如图,在四棱锥中,,分别是,的中点,,,,,,,,.
(Ⅰ)证明:平面;
(Ⅱ)求直线与平面所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ).
【分析】
(Ⅰ)要证明线面平行,根据判断定理,需证明线线平行,做辅助线,连接,交于,再连接,证明,即可证明;(Ⅱ)点到平面的距离转化为点到平面的距离的2倍,利用,即上任何一个点到平面的距离相等,通过做辅助线转化.
【详解】
(Ⅰ)连接,交于,再连接
因为,是的中点,所以是的中点,
又是的中点,
所以,且平面,平面
所以平面;
(Ⅱ)过作于,连接,
又因为,且
所以平面,
所以平面,
所以平面平面,过作于,
又因为平面平面,
且平面,
所以平面.
在中,,
在直角梯形中,,则
在中,,
在中,,,,
则,
所以,从而,
又由,,知,
所以由可得,
因为点到平面的距离是点到平面的距离的2倍,点到平面的距离和点到平面距离相等,所以点到平面的距离是点到平面的距离的2倍,
所以直线与平面所成角的正弦值为.
88.设P为多面体M的一个顶点,定义多面体M在点P处的离散曲率为,其中Qi(i=1,2,…,k,k≥3)为多面体M的所有与点P相邻的顶点,且平面Q1PQ2,平面Q2PQ3,…,平面Qk﹣1PQk和平面QkPQ1遍历多面体M的所有以P为公共点的面.
(1)如图1,已知长方体A1B1C1D1﹣ABCD,AB=BC=1,,点P为底面A1B1C1D1内的一个动点,则求四棱锥P﹣ABCD在点P处的离散曲率的最小值;
(2)图2为对某个女孩面部识别过程中的三角剖分结果,所谓三角剖分,就是先在面部取若干采样点,然后用短小的直线段连接相邻三个采样点形成三角形网格.区域α和区域β中点的离散曲率的平均值更大的是哪个区域?(确定“区域α”还是“区域β”)
【答案】(1);(2)区域β.
【分析】
(1)计∠Q1PQ2+∠Q2PQ3+…+∠QnPQ1=θ,则离散曲率为1﹣,θ越大离散曲率越小.由四棱锥的性质求得θ=,可求得四棱锥P﹣ABCD在点P处的离散曲率的最小值;
(2)区域β比区域α更加平坦,所以θ更大,离散曲率更小.可得答案.
【详解】
(1)计∠Q1PQ2+∠Q2PQ3+…+∠QnPQ1=θ,则离散曲率为1﹣,θ越大离散曲率越小.
P在底面ABCD的投影记为H,通过直观想象,当H点在平面ABCD中逐渐远离正方形ABCD的中心,以至于到无穷远时,θ逐渐减小以至于趋近于0.所以当H点正好位于正方形ABCD的中心时,θ最大,离散曲率最小.此时HA=HB==PH,所以PA=PB=1=AB,所以∠APB=60°,θ=,
离散曲率为1﹣×=,所以四棱锥P﹣ABCD在点P处的离散曲率的最小值为;
(2)区域β比区域α更加平坦,所以θ更大,离散曲率更小.
所以区域α和区域β中点的离散曲率的平均值更大的是区域β.
89.如图,四棱锥的底面是边长为的正方形,.
(1)证明:;
(2)当直线与平面所成角的正弦值最大时,求此时二面角的大小.
【答案】(1)证明见解析;(2).
【分析】
(1)分别取、的中点、,连接、、,证明出,可证得,由此可证得结论成立;
(2)推导出为二面角的平面角,设,可得出,以点为坐标原点,、所在直线分别为、轴建立空间直角坐标系,利用空间向量法结合基本不等式求出直线与平面所成角的正弦值的最大值,求出对应的值,即可得解.
【详解】
(1)分别取、的中点、,连接、、.
因为,为的中点,所以.
又因为,所以.
因为四边形为正方形,则且,
、分别为、的中点,且,
,所以,四边形为矩形,则,
,所以平面.
因为平面,所以.
在中,为的中点,,所以.
又因为,,所以,从而可得;
(2)由(1)可知,平面,,平面,
平面,,所以,为二面角的平面角,且,
以点为坐标原点,、所在直线分别为、轴建立如下图所示的空间直角坐标系,
设,其中,则、、、、、,
,,,
设平面的法向量为,
由,即,
取,则,,,
,
令,则,
则,
当且仅当时,即当时,即当时,等号成立.
所以,当直线与平面所成角的正弦值最大时,二面角为.
90.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是,所以正四面体在各顶点的曲率为,故其总曲率为.
(1)求四棱锥的总曲率;
(2)若多面体满足:顶点数-棱数+面数,证明:这类多面体的总曲率是常数.
【答案】(1);(2)证明见解析.
【分析】
(1)四棱锥的总曲率等于四棱锥各顶点的曲率之和,写出多边形表面的所有内角即可.(2)设顶点数、棱数、面数分别为、、,设第个面的棱数为,所以,按照公式计算总曲率即可.
【详解】
(1)由题可知:四棱锥的总曲率等于四棱锥各顶点的曲率之和.
可以从整个多面体的角度考虑,所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知:四棱锥共有5个顶点,5个面,其中4个为三角形,1个为四边形.
所以四棱锥的表面内角和由4个为三角形,1个为四边形组成,
则其总曲率为:.
(2)设顶点数、棱数、面数分别为、、,所以有
设第个面的棱数为,所以
所以总曲率为:
所以这类多面体的总曲率是常数.
91.已知四棱锥的底面是平行四边形,平面与直线,,分别交于点,,且,点在直线上,为的中点,且直线平面.
(1)设,,,试用基底表示向量;
(2)证明,四面体中至少存在一个顶点从其出发的三条棱能够组成一个三角形;
(3)证明,对所有满足条件的平面,点都落在某一条长为的线段上.
【答案】(1);(2)证明见解析;(3)证明见解析.
【分析】
(1)利用向量加减法的几何意义有,,即可求;
(2)假设四面体的最长棱为,只需以为顶点的其它两组棱中或即得证至少存在一个顶点从其出发的三条棱能够组成一个三角形;
(3)由平面,令结合向量共面定理有,即得一元二次方程在有解,求的范围且范围长度为即得证.
【详解】
(1)∵,而,
∴,
所以.
(2)不妨设是四面体最长的棱,则在,中,,,
∴,即,
故,至少有一个大于,不妨设,
∴,,构成三角形.
(3)设,,,由(1)知.
又,有,,,
∴,
,
,
设,又
∴
因为平面,所以存在实数,使得:,
∴
∴,消元:在有解.
当时,,即;
当时,,解得.
综上,有.
所以对所有满足条件的平面,点都落在某一条长为的线段上.
92.如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是菱形,∠ABC=,∠B1BD=,
(1)求证:直线AC⊥平面BDB1;
(2)求直线A1B1与平面ACC1所成角的正弦值.
【答案】(1)证明见解析;(2)
【分析】
(1)由边角边证得,即,在等腰三角形中由三线合一证得,在菱形中由菱形的对角线垂直证得,由线面垂直的判定定理说明即得证;
(2)延长交于点,平面即为平面,平面即平面,由(1)得平面平面,平面平面,所以过做,由面面垂直的性质则平面,故即为直线与平面所成角(若研究直线与平面所成角的正弦值则线段等比例扩大2倍结果不变),在菱形ABCD中求出BD,作,由和勾股定理可求得,由余弦定理和同角三角函数关系求得,,进而求得,最后由正弦函数定义可求得答案;也可以利用建立空间直角坐标系的方式运算求解.
【详解】
(1)连接交于,
因为,,,
所以,故
又因为为菱形对角线交点,即是线段的中点,所以
又四边形为菱形,故
而,所以平面
方法二:因为,
所以点在平面内的射影在为的平分线,
又四边形为菱形,故为的平分线,则直线
故平面平面,而平面平面,
又四边形为菱形,故
所以平面
(2)延长交于点,平面即为平面,平面即平面
由(1)得平面平面,平面平面,
所以过做,则平面,故即为直线与平面所成角(若研究直线与平面所成角的正弦值则线段等比例扩大2倍结果不变)
因为四棱台中,所以,
由菱形有,且∠ABC=,所以,
作,因为,则,,所以,
则,,,
故.
法二:延长交于点,
平面即为平面,平面即平面,
设直线与平面所成角为
过作,垂足为,因为,所以
建系,以为轴,作轴,
设平面的法向量为,则
,
所以,
所以
93.如图1所示为一种魔豆吊灯,图2为该吊灯的框架结构图,由正六棱锥和构成,两个棱锥的侧棱长均相等,且棱锥底面外接圆的直径为,底面中心为,通过连接线及吸盘固定在天花板上,使棱锥的底面呈水平状态,下顶点与天花板的距离为,所有的连接线都用特殊的金属条制成,设金属条的总长为y.
(1)设∠O1AO =(rad),将y表示成θ的函数关系式,并写出θ的范围;
(2)请你设计θ,当角θ正弦值的大小是多少时,金属条总长y最小.
【答案】(1),(,).(2)当角满足()时,金属条总长y最小.
【分析】
(1)在直角三角形OAO1中,利用三角函数的定义,用表示,其中由实际问题可得θ的范围,最后把吊灯12条侧棱,6条底边,1条顶悬长相加表示y,得答案;
(2)为了方便运算,只令,利用求导的方式得极值,此时即为最小值.
【详解】
(1)在直角三角形OAO1中,,,
由,所以,
所以θ的范围是,其中,.
从而有
,
所以,(,).
(2)令,所以,
令,则,则.
当时,;当时,.
函数的单调性与关系列表如下:
0
+
极小值
所以当,其中时取得最小值,即y最小.
故当角满足()时,金属条总长y最小.
94.如图,菱形的边长为2,现将沿对角线AC折起至位置,并使平面平面.
(1)求证:;
(2)在菱形中,若,求直线AB与平面PBC所成角的正弦值;
(3)求四面体PABC体积的最大值.
【答案】(1)证明见解析;(2);(3).
【详解】
试题分析:(1)要证线线垂直,就是要证线面垂直,由于是菱形,因此取中点则有,这样可得线面垂直,从而得结论线线垂直;(2)在(1)的证明中正好有三线两两垂直,因此以它们为坐标轴,建立空间直角坐标系,用空间向量法求出直线与平面所成角;(3)引入一个参数,设,则,,(),变形有
,用均值不等式可求得最大值,也可设,然后用导数的方法求得最大值.
试题解析:(1)证明:取中点,连接,由于四边形为菱形,
,又,
平面,又平面,.
(2)平面平面, 平面平面,,,
两两垂直,
故以为原点,以方向分别为轴正方向建立空间直角坐标系,
,菱形的边长为,
∴,
,
设平的法向量,直线与平成角为,
∴,取,则,于是,
∴, ∴直线与平面成角的正弦值为.
(3)法一:
设, ∴,,
又平面ABC, ∴
(),
∴
,
∴,当且仅当,即时取等号,
∴四面体PABC体积的最大值为.
法二:设,
∴,,又平面ABC,
∴
(),
设,则,且,
∴,
∴当时,,当时,,
∴当时,取得最大值,∴四面体PABC体积的最大值为.
法三:设,则,,
又平面ABC,
∴,
∵,
当且仅当,即时取等号,∴四面体PABC体积的最大值为.
95.在①平面,②平面平面,③这三个条件中任选一个,补充在下面的问题中,并解决该问题.
问题:如图,在三棱锥中,平面平面,是以为斜边的等腰直角三角形,,,为中点,为内的动点(含边界).
(1)求点到平面的距离;
(2)若__________,求直线与平面所成角的正弦值的取值范围.
注:若选择多个条件分别解答,按第一个解答计分.
【答案】(1);(2).
【分析】
(1)利用等体积,转换顶点即可;(2)建立空间直角坐标系,求其法向量,表示出线面角的正弦值,按照求值域的思路适当换元求范围即可.
【详解】
(1)在三棱锥中,连接,,
因为是以为斜边的等腰直角三角形,,为中点,
所以,
又平面平面,平面平面,平面
∴平面
又平面∴∴,,两两垂直.
∴
又
∴
∴点到平面的距离为.
(2)与平面所成角的正弦值的取值范围为.
以选条件①为例(亦可使用综合法、综合与向量混用法)
在三棱锥中,以为坐标原点,为正交基底,
建立空间直角坐标系,
则,,,,,
设,则,,,
,
设平面的法向量为,则
即即,
不妨令,则
同理可求得平面的法向量
(选条件①)因为平面,平面
∴即
即∴
又∴∴
又平面,∴是平面的一个法向量
设直线与平面所成角为,则
令,,
∴
令,则
∴在上单调递增
∴,∴,∴
∴直线与平面所成角的正弦值的取值范围为.
选条件②,条件③结果相同.
96.如下图,在四棱锥中,已知平面,且四边形为直角梯形,,,.
(1)求平面与平面夹角的余弦值;
(2)定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值,利用此定义求异面直线与之间的距离.
【答案】(1);(2)
【分析】
(1)以为正交基底建立如图所示的空间直角坐标系,求出平面PAB和平面PCD的法向量,利用夹角公式求解即可;
(2)设为直线PB上一点,且,利用坐标运算求出点到直线的距离,求出最值即可.
【详解】
解:以为正交基底建立如图所示的空间直角坐标系,
则各点的坐标为B(1,0,0),,,
(1)因为平面,且面,
,又,且,
AD⊥平面PAB,
所以是平面PAB的一个法向量,
因为,.
设平面PCD的法向量为,
则,
即,令,解得,.
所以是平面PCD的一个法向量,
从而,
所以平面PAB与平面PCD所成二面角的余弦值为;
(2)因为,
设为直线PB上一点,且,
又,
则,
则点到直线的距离
∵
∴
所以异面直线PB与CD之间的距离为.
97.椭圆的左、右焦点分别为、.经过点且倾斜角为的直线与椭圆交于A、B两点(其中点A在x轴上方),的周长为8.
(1)求椭圆的标准方程;
(2)如图,把平面沿x轴折起来,使y轴正半轴和x轴所确定的半平面,与y轴负半轴和x轴所确定的半平面互相垂直:
①若,求异面直线和所成角的大小;
②若折叠后的周长为,求的大小.
【答案】(1);(2)①;②.
【分析】
(1)根据条件求得,即得,即得椭圆方程;
(2)①先根据直线方程与椭圆方程解得A,B坐标,再建立空间直角坐标系,利用空间向量数量积求线线角;
②设折叠前,,则得折叠后A,B坐标,代入化简周长条件,再利用直线方程 与椭圆方程联立方程组,结合韦达定理代入化简条件,解得,即得的大小.
【详解】
(1)因为的周长为8,所以.
由题意得
所以椭圆的方程为.
(2)①由直线与 联立求得,(因为点A在x轴上方)以及
再以O为坐标原点,折叠后原y轴负半轴,原x轴,原y轴正半轴所在直线为x,y,z轴建立空间直角坐标系,则
,. ,,, .
异面直线和所成角为,则
所求角为
②由, ,故
由, ,故
设折叠前, .
直线与椭圆联立方程,得
, .
在折叠后的图形中建立如图所示的空间直角坐标系(原x轴仍然为x轴,原y轴正半轴为y轴,原y轴负半轴为z轴):
设A,B在新图形中对应点记为,,
,
,
( i)
所以( ii)
由(i)(ii)可得
, ,
解得,,所以
98.某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆及其内接等腰三角形绕底边上的高所在直线旋转而成,如图2.已知圆的半径为10cm,设,圆锥的侧面积为cm2.
(1)求关于的函数关系式;
(2)为了达到最佳观赏效果,要求最大,求的最大值并求此时腰的长度.
【答案】(1),;(2)的最大值为,的长度为cm..
【分析】
(1)利用含的式子表示出圆锥的母线,表示出圆锥的底面半径,计算出底面圆的周长即为圆锥侧面展开扇形的弧长,再根据扇形面积公式表示出;
(2)由(1)可知的表达式,代入得关于的表达式,然后利用三角恒等变换公式进行化简整理,结合三角函数知识分析其最值.
【详解】
解:(1)设交于点,过作,垂足为,
在中,,,
在中,,
所以,
(2)由(1)得:
当时,的最大值为.
此时,,为正三角形.此时,.
答:的最大值为,此时的长度为cm.
99.如图,在直四棱柱中,底面是边长为1的菱形,侧棱长为2.
(1)与能否垂直?说明理由;
(2)当在上变化时,求异面直线与所成角的取值范围.
【答案】(1)不能.见解析;(2)
【分析】
(1)以分别为,,轴建立空间直角坐标系,设,进而得到,结合向量的数量积的运算,即可求解;
(2)求得,求得,根据,设,化简得到,再由题设条件和二次函数的性质,即可求解.
【详解】
由题意,菱形中,于,设,
以分别为,,轴建立空间直角坐标系,
设,则,
(1)因为,
可得,所以与不能垂直.
(2)因为,所以,
由,所以,则,
又由,
所以,
因为,设,
因为,所以,所以,
所以,
因为,可得,
所以异面直线与所成角的取值范围.
100.如图,一条东西流向的笔直河流,现利用航拍无人机监控河流南岸相距150米的两点处(在的正西方向),河流北岸的监控中心在的正北方100米处,监控控制车在的正西方向,且在通向的沿河路上运动,监控过程中,保证监控控制车到无人机和到监控中心的距离之和150米,平面始终垂直于水平面,且,两点间距离维持在100米.
(1)当监控控制车到监控中心的距离为100米时,求无人机距离水平面的距离;
(2)若记无人机看处的俯角(),监控过程中,四棱锥内部区域的体积为监控影响区域,请将表示为关于的函数,并求出监控影响区域的最大值.
【答案】(1)米;(2),立方米
【分析】
(1)过D作,垂足为F,由面面垂直的性质定理可知,平面ABCE,即线段DF长为点D到平面ABCE的距离,在中利用面积相等求出DF即可;
(2)由(1)知,DF是四棱锥D-ABCE的高,在中,把DF表示成关于的表达式,再利用四棱锥的体积公式把四棱锥内部区域的体积为监控影响区域表示成关于的函数,对函数进行求导,利用导数判断其单调性并求其最大值.
【详解】
(1)过D作,垂足为F,
又因为平面平面ABCE,平面平面,
所以平面ABCE,
所以线段DF长为点D到平面ABCE的距离,
在中,,(米),(米),
所以(米).
即点D到水平面ABCE的距离为米.
(2)由(1)知,DF是四棱锥D-ABCE的高,
在中,因为(米),,
所以(米),(米),
所以(米),
所以梯形ABCE的面积(米),
所以四棱锥的体积
,
分析知,,且,
所以V关于的函数关系为
,
.
因为,
所以当时,;当时,,
即当时,函数单调递增;当时,函数单调递减,
所以当,即时,
(立方米).
即监控影响区域的最大值为立方米.
相关试卷
这是一份专题37 导数证明恒成立问题大题-2022年新高考数学高频考点 题型专项练习(新高考适用),文件包含专题37导数证明恒成立问题大题解析版docx、专题37导数证明恒成立问题大题原卷版docx等2份试卷配套教学资源,其中试卷共154页, 欢迎下载使用。
这是一份专题30 圆锥曲线求过定点大题-2022年新高考数学高频考点 题型专项练习(新高考适用),文件包含专题30圆锥曲线求过定点大题解析版docx、专题30圆锥曲线求过定点大题原卷版docx等2份试卷配套教学资源,其中试卷共167页, 欢迎下载使用。
这是一份专题23 概率统计综合大题-2022年新高考数学高频考点 题型专项练习(新高考适用),文件包含专题23概率统计综合大题解析版docx、专题23概率统计综合大题原卷版docx等2份试卷配套教学资源,其中试卷共223页, 欢迎下载使用。









