（全国通用）2022年中考数学一轮复习高频考点精讲精练 专题15 反比例函数（原卷版+解析版）学案

这是一份（全国通用）2022年中考数学一轮复习高频考点精讲精练 专题15 反比例函数（原卷版+解析版）学案，文件包含全国通用2022年中考数学一轮复习高频考点精讲精练专题15反比例函数解析版docx、全国通用2022年中考数学一轮复习高频考点精讲精练专题15反比例函数原卷版docx等2份学案配套教学资源，其中学案共33页， 欢迎下载使用。

【高频考点精讲】
1．用描点法画反比例函数的图象，步骤：列表—描点—连线．
（1）列表取值时，x≠0，因为x＝0函数无意义，为了使描出的点具有代表性，可以以“0”为中心，向两边对称式取值，即正、负数各一半，且互为相反数，这样也便于求y值。
（2）由于函数图象的特征还不清楚，所以要尽量多取数值，多描点，便于连线，使画出的图象更精确。
（3）连线时要用平滑的曲线按照自变量从小到大的顺序连接。
（4）由于x≠0，k≠0，所以y≠0，函数图象永远不会与x轴、y轴相交，只是无限靠近两坐标轴。
2．反比例函数的性质
（1）反比例函数y＝（k≠0）的图象是双曲线；
（2）当k＞0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小；
（3）当k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大；
注意：反比例函数的图象与坐标轴没有交点。
【热点题型精练】
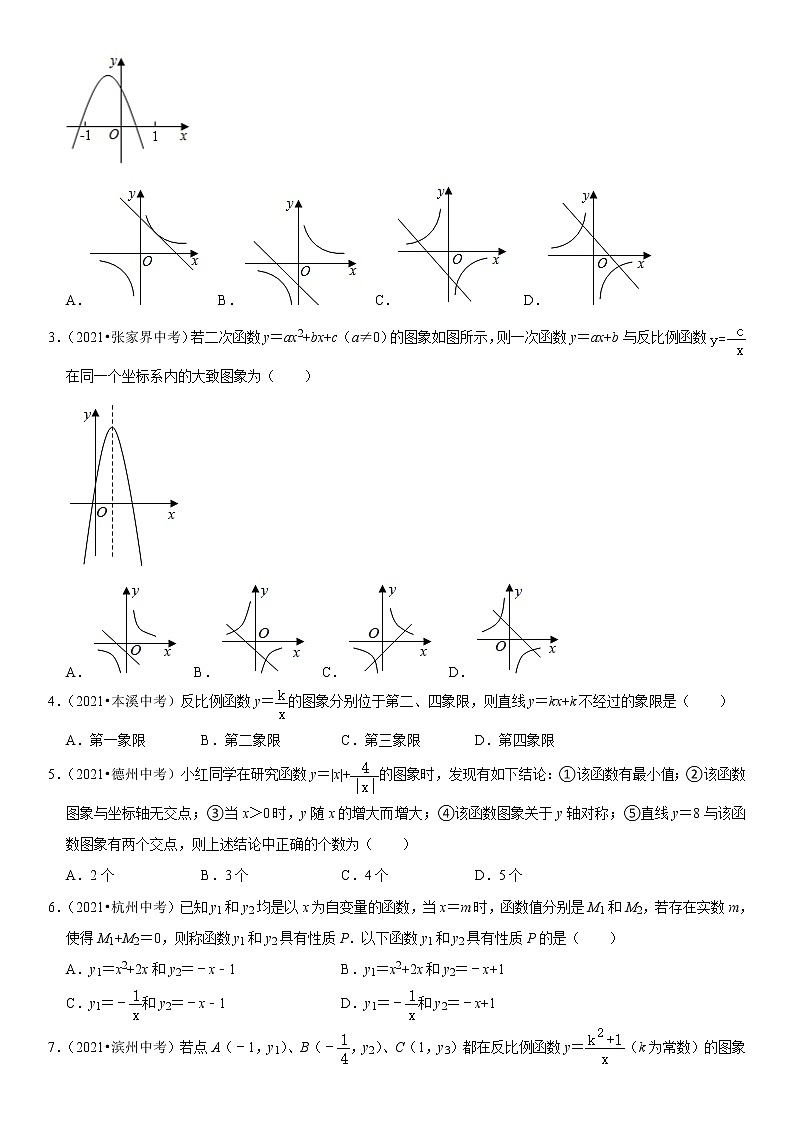
1．（2021•荆门中考）在同一平面直角坐标系中，函数y＝kx﹣k与y＝（k≠0）的大致图象是（ ）
A．①②B．②③C．②④D．③④
解：当k＞0时，
一次函数y＝kx﹣k经过一、三、四象限，
函数y＝（k≠0）的图象在一、二象限，
故选项②的图象符合要求．
当k＜0时，
一次函数y＝kx﹣k经过一、二、四象限，
函数y＝（k≠0）的图象经过三、四象限，
故选项③的图象符合要求．
答案：B．
2．（2021•聊城中考）已知二次函数y＝ax2+bx+c的图象如图所示，则一次函数y＝bx+c的图象和反比例函数y＝的图象在同一坐标系中大致为（ ）
A． B． C． D．
解：∵二次函数的图象开口向下，
∴a＜0，
∵﹣＜0，
∴b＜0，
∵抛物线与y轴相交于正半轴，
∴c＞0，
∴直线y＝bx+c经过一、二、四象限，
由图象可知，当x＝1时，y＜0，
∴a+b+c＜0，
∴反比例函数y＝的图象必在二、四象限，
故A、B、C错误，D正确；
答案：D．
3．（2021•张家界中考）若二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则一次函数y＝ax+b与反比例函数在同一个坐标系内的大致图象为（ ）
A． B． C． D．
解：∵抛物线开口向下，对称轴位于y轴右侧，与y轴的交点在y轴正半轴上，
∴a＜0，﹣＞0，c＞0，
∴b＞0，
∴一次函数y＝ax+b的图象经过第一、二、四象限，反比例函数y＝﹣的图象在第二、四象限．
答案：D．
4．（2021•本溪中考）反比例函数y＝的图象分别位于第二、四象限，则直线y＝kx+k不经过的象限是（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
解：∵反比例函数y＝的图象分别位于第二、四象限，
∴k＜0，
∴一次函数y＝kx+k的图象经过第二、三、四象限，即不经过第一象限．
答案：A．
5．（2021•德州中考）小红同学在研究函数y＝|x|+的图象时，发现有如下结论：①该函数有最小值；②该函数图象与坐标轴无交点；③当x＞0时，y随x的增大而增大；④该函数图象关于y轴对称；⑤直线y＝8与该函数图象有两个交点，则上述结论中正确的个数为（ ）
A．2个B．3个C．4个D．5个
解：列表：
画出函数图象如图，
观察图象：
①该函数有最小值，符合题意；
②该函数图象与坐标轴无交点，符合题意；
③当x＞0时，y随x的增大而增大，不合题意；
④该函数图象关于y轴对称，符合题意；
⑤令|x|+＝8，整理得x2﹣8x+4＝0或x2+8x+4＝0，
∵Δ＝82﹣4×1×4＞0，
∴两个方程均有两个不相等的实数根，即共有四个根，且这四个根互不相等．
∴直线y＝8与该函数图象有四个交点，不符合题意，
综上，以上结论正确的有：①②④，
答案：B．
6．（2021•杭州中考）已知y1和y2均是以x为自变量的函数，当x＝m时，函数值分别是M1和M2，若存在实数m，使得M1+M2＝0，则称函数y1和y2具有性质P．以下函数y1和y2具有性质P的是（ ）
A．y1＝x2+2x和y2＝﹣x﹣1B．y1＝x2+2x和y2＝﹣x+1
C．y1＝﹣和y2＝﹣x﹣1D．y1＝﹣和y2＝﹣x+1
解：A．令y1+y2＝0，则x2+2x﹣x﹣1＝0，解得x＝或x＝，即函数y1和y2具有性质P，符合题意；
B．令y1+y2＝0，则x2+2x﹣x+1＝0，整理得，x2+x+1＝0，方程无解，即函数y1和y2不具有性质P，不符合题意；
C．令y1+y2＝0，则﹣﹣x﹣1＝0，整理得，x2+x+1＝0，方程无解，即函数y1和y2不具有性质P，不符合题意；
D．令y1+y2＝0，则﹣﹣x+1＝0，整理得，x2﹣x+1＝0，方程无解，即函数y1和y2不具有性质P，不符合题意；
答案：A．
7．（2021•滨州中考）若点A（﹣1，y1）、B（﹣，y2）、C（1，y3）都在反比例函数y＝（k为常数）的图象上，则y1、y2、y3的大小关系为 y2＜y1＜y3 ．
解：∵反比例函数y＝（k为常数），k2+1＞0，
∴该函数图象在第一、三象限，在每个象限内y随x的增大而减小，
∵点A（﹣1，y1）、B（﹣，y2）、C（1，y3）都在反比例函数y＝（k为常数）的图象上，﹣1＜﹣，点A、B在第三象限，点C在第一象限，
∴y2＜y1＜y3，
答案：y2＜y1＜y3．
8．（2021•临沂中考）已知函数y＝
（1）画出函数图象；
列表：
描点，连线得到函数图象：
（2）该函数是否有最大或最小值？若有，求出其值，若没有，简述理由；
（3）设（x1，y1），（x2，y2）是函数图象上的点，若x1+x2＝0，证明：y1+y2＝0．
解：（1）列表如下：
函数图象如图所示：
（2）根据图象可知：
当x＝1时，函数有最大值3；当x＝﹣1时，函数有最小值﹣3．
（3）∵（x1，x2）是函数图象上的点，x1+x2＝0，
∴x1和x2互为相反数，
当﹣1＜x1＜1时，﹣1＜x2＜1，
∴y1＝3x1，y2＝3x2，
∴y1+y2＝3x1+3x2＝3（x1+x2）＝0；
当x1≤﹣1时，x2≥1，
则y1+y2＝＝0；
同理：当x1≥1时，x2≤﹣1，
y1+y2＝0，
综上：y1+y2＝0．
二、反比例函数图象上点的坐标特征及系数k的几何意义
【高频考点精讲】
1．反比例函数y＝（k为常数，k≠0）的图象是双曲线
（1）图象上的点（x，y）的横纵坐标的积是定值k，即x y＝k；
（2）双曲线是关于原点对称的，两个分支上的点也是关于原点对称；
（3）在y＝图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|。
2．比例系数k的几何意义
在反比例函数y＝图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|；
在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k|，
且保持不变。
【热点题型精练】
9．（2021•广州中考）在平面直角坐标系xOy中，矩形OABC的点A在函数y＝（x＞0）的图象上，点C在函数y＝﹣（x＜0）的图象上，若点B的横坐标为﹣，则点A的坐标为（ ）
A．（，2）B．（，）C．（2，）D．（，）
解：如图，作AD⊥x轴于D，CE⊥x轴于E，
∵四边形OABC是矩形，
∴∠AOC＝90°，
∴∠AOD+∠COE＝90°，
∵∠AOD+∠OAD＝90°，
∴∠COE＝∠OAD，
∵∠CEO＝∠ODA，
∴△COE∽△OAD，
∴＝（）2，，
∵S△COE＝×|﹣4|＝2，S△AOD＝＝，
∴＝，
∴OE＝2AD，CE＝2OD，
设A（m，）（m＞0），
∴C（﹣，2m），
∴OE＝0﹣（﹣）＝，
∵点B的横坐标为﹣，
∴m﹣（﹣）＝，
整理得2m2+7m﹣4＝0，
∴m1＝，m2＝﹣4（舍去），
经检验，m＝是方程的解，
∴A（，2），
答案：A．
10．（2021•长春中考）如图，在平面直角坐标系中，点A、B在函数y＝（k＞0，x＞0）的图象上，过点A作x轴的垂线，与函数y＝﹣（x＞0）的图象交于点C，连结BC交x轴于点D．若点A的横坐标为1，BC＝3BD，则点B的横坐标为（ ）
A．B．2C．D．3
解：作BE⊥x轴于E，
∴AC∥BE，
∴△CDF∽△BDE，
∴＝＝，
∵BC＝3BD，
∴＝＝，
∴CF＝2BE，DF＝2DE，
设B（，b），
∴C（1，﹣2b），
∵函数y＝﹣（x＞0）的图象交于点C，
∴﹣k＝1×（﹣2b）＝﹣2b，
∴k＝2b，
∴B的横坐标为＝＝2，
答案：B．
11．（2021•十堰中考）如图，反比例函数y＝（x＞0）的图象经过点A（2，1），过A作AB⊥y轴于点B，连OA，直线CD⊥OA，交x轴于点C，交y轴于点D，若点B关于直线CD的对称点B′恰好落在该反比例函数图象上，则D点纵坐标为（ ）
A．B．C．D．
解：设BB′交直线CD于点E，过点E作EG⊥BD于G，过B′作B′F⊥BD于点F，如图，
∵B与B′关于直线CD对称，
∴CD垂直平分BB′．
即E为BB′的中点，EB＝EB′．
∵EG⊥BD，B′F⊥BD，
∴EG∥B′F．
∴EG＝B′F．
∵直线OA经过点A（2，1），
∴直线OA的解析式为：y＝x．
∵CD⊥OA，BB′⊥CD，
∴BB′∥OA．
设直线BB′的解析式为y＝x+b，
∵B（0，1），
∴b＝1．
∴直线BB′的解析式为y＝x+1．
∵反比例函数y＝（x＞0）的图象经过点A（2，1），
∴反比例函数y＝．
联立方程得：．
解得：，．
∴B′（）．
∴B′F＝．
∴EG＝．
∵AB⊥BD，
∴∠OAB＝∠ODC．
∴tan∠OAB＝tan∠ODC＝．
在Rt△DGE中，
∵tan∠ODC＝，
∴DG＝﹣1．
同理：BG＝．
∴OD＝OB+BG+DG＝．
∴D点纵坐标为．
答案：A．
12．（2021•武汉中考）已知点A（a，y1），B（a+1，y2）在反比例函数y＝（m是常数）的图象上，且y1＜y2，则a的取值范围是 ﹣1＜a＜0 ．
解：∵k＝m2+1＞0，
∴反比例函数y＝（m是常数）的图象在一、三象限，在每个象限，y随x的增大而减小，
①当A（a，y1），B（a+1，y2）在同一象限，
∵y1＜y2，
∴a＞a+1，
此不等式无解；
②当点A（a，y1）、B（a+1，y2）在不同象限，
∵y1＜y2，
∴a＜0，a+1＞0，
解得：﹣1＜a＜0，
答案：﹣1＜a＜0．
13．（2021•深圳中考）如图，已知反比例函数过A，B两点，A点坐标（2，3），直线AB经过原点，将线段AB绕点B顺时针旋转90°得到线段BC，则C点坐标为 （4，﹣7） ．
解：∵A点坐标（2，3），直线AB经过原点，
∴B（﹣2，﹣3）
过点B作x轴的平行线l过点A，点C作l的垂线，分别交于D，E两点，则D（2，﹣3），
∵∠ABD+∠CBE＝90°，∠ABD+∠BAD＝90°，
∴∠CBE＝∠BAD，
在△ABD与△BEC 中，
，
∴△ABD≌△BEC（AAS），
∴BE＝AD＝6，CE＝BD＝4，
∴C（4，﹣7），
答案：（4，﹣7）．
14．（2021•温州中考）如图，点A，B在反比例函数y＝（k＞0，x＞0）的图象上，AC⊥x轴于点C，BD⊥x轴于点D，BE⊥y轴于点E，连结AE．若OE＝1，OC＝OD，AC＝AE，则k的值为（ ）
A．2B．C．D．2
解：∵BD⊥x轴于点D，BE⊥y轴于点E，
∴四边形BDOE是矩形，
∴BD＝OE＝1，
把y＝1代入y＝，求得x＝k，
∴B（k，1），
∴OD＝k，
∵OC＝OD，
∴OC＝k，
∵AC⊥x轴于点C，
把x＝k代入y＝得，y＝，
∴AE＝AC＝，
∵OC＝EF＝k，AF＝﹣1＝，
在Rt△AEF中，AE2＝EF2+AF2，
∴（）2＝（k）2+（）2，解得k＝±，
∵在第一象限，
∴k＝，
答案：B．
15．（2021•绥化中考）如图，在平面直角坐标系中，O为坐标原点，MN垂直于x轴，以MN为对称轴作△ODE的轴对称图形，对称轴MN与线段DE相交于点F，点D的对应点B恰好落在y＝（k≠0，x＜0）的双曲线上，点O、E的对应点分别是点C、A．若点A为OE的中点，且S△AEF＝1，则k的值为 ﹣24 ．
解：如图，MN交x轴于点G，连接OB，
由于Rt△DOE与Rt△BCA关于MN成轴对称，且OA＝AE，
由对称性可知，AG＝GE，OA＝AE＝EC，
∴AG＝AC，
∵S△AEF＝1，
∴S△AFG＝S△AEF＝，
∵MN∥BC∥OD，
∴△AFG∽△ABC，
∴＝（）2＝，
∴S△ABC＝×16＝8，
又∵OA＝AC，
∴S△OAB＝S△ABC＝4，
∴S△OBC＝8+4＝12，
∵点B在反比例函数y＝的图象上，
∴S△OBC＝12＝|k|，
∵k＜0，
∴k＝﹣24，
答案：﹣24．
16．（2021•日照中考）如图，在平面直角坐标系xOy中，正方形OABC的边OC、OA分别在x轴和y轴上，OA＝10，点D是边AB上靠近点A的三等分点，将△OAD沿直线OD折叠后得到△OA′D，若反比例函数y＝（k≠0）的图象经过A′点，则k的值为 48． ．
解：过A′作EF⊥OC于F，交AB于E，
∵∠OA′D＝90°，
∴∠OA′F+∠DA′E＝90°，
∵∠OA′F+∠A′OF＝90°，
∴∠DA′E＝∠A′OF，
∵∠A′FO＝∠DEA′，
∴△A′OF∽△DA′E，
∴＝＝，
设A′（m，n），
∴OF＝m，A′F＝n，
∵正方形OABC的边OC、OA分别在x轴和y轴上，OA＝10，点D是边AB上靠近点A的三等分点，
∴DE＝m﹣，A′E＝10﹣n，
∴＝＝3，
解得m＝6，n＝8，
∴A′（6，8），
∵反比例函数y＝（k≠0）的图象经过A′点，
∴k＝6×8＝48，
答案：48．
17．（2021•绍兴中考）如图，在平面直角坐标系中，正方形ABCD的顶点A在x轴正半轴上，顶点B，C在第一象限，顶点D的坐标（，2）．反比例函数y＝（常数k＞0，x＞0）的图象恰好经过正方形ABCD的两个顶点，则k的值是 5或22.5 ．
解：作DM⊥x轴于M，BN⊥x轴于N，过C点作x轴的平行线，交DM于E，交BN于F，
正方形ABCD中，∠BAD＝90°，
∴∠DAM+∠BAN＝90°，
∵∠ADM+∠DAM＝90°，
∴∠ADM＝∠BAN，
在△ADM和△BAN中，
，
∴△ADM≌△BAN（AAS），
∴AM＝BN，DM＝AN，
∵顶点D的坐标（，2）．
∴OM＝，DM＝2，
同理：△ADM≌△DCE，
∴AM＝DE，CE＝DM，
∴AM＝BN＝DE，DM＝AN＝CE＝2，
设AM＝BN＝DE＝m，
∴ON＝+m+2＝4.5+m，
∴B（4.5+m，m），C（4.5，2+m），
当反比例函数y＝（常数k＞0，x＞0）的图象经过点B、D时，则k＝×2＝5；
当反比例函数y＝（常数k＞0，x＞0）的图象经过点B、C时，则k＝（4.5+m）•m＝4.5•（2+m），
解得m＝3（负数舍去），
∴k＝4.5×（2+3）＝22.5，
答案：5或22.5．
18．（2021•无锡中考）一次函数y＝x+n的图象与x轴交于点B，与反比例函数y＝（m＞0）的图象交于点A（1，m），且△AOB的面积为1，则m的值是（ ）
A．1B．2C．3D．4
解：在y＝x+n中，令y＝0，得x＝﹣n，
∴B（﹣n，0），
∵A（1，m）在一次函数y＝x+n的图象上，
∴m＝1+n，即n＝m﹣1，
∴B（1﹣m，0），
∵△AOB的面积为1，m＞0，
∴OB•|yA|＝1，即|1﹣m|•m＝1，
解得m＝2或m＝﹣1（舍去），
∴m＝2，
答案：B．
三、反比例函数与一次函数的交点问题
【高频考点精讲】
1．求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点；
2．判断正比例函数y＝k1x和反比例函数y＝在同一直角坐标系中的交点个数可总结为：
（1）当k1与k2同号时，正比例函数y＝k1x和反比例函数y＝在同一直角坐标系中有2个交点；
（2）当k1与k2异号时，正比例函数y＝k1x和反比例函数y＝在同一直角坐标系中有0个交点。
【热点题型精练】
19．（2021•南通中考）平面直角坐标系xOy中，直线y＝2x与双曲线y＝（k＞2）相交于A，B两点，其中点A在第一象限．设M（m，2）为双曲线y＝（k＞2）上一点，直线AM，BM分别交y轴于C，D两点，则OC﹣OD的值为（ ）
A．2B．4C．6D．8
解：取k＝8，如图，则M（4，2），A（2，4），B（﹣2，﹣4），
得AM的解析式为：y＝﹣x+6，BM的解析式为：y＝x﹣2，
∴OC＝6，OD＝2，
∴OC﹣OD＝6﹣2＝4．
答案：B．
20．（2021•枣庄中考）如图，正比例函数y1＝k1x（k1≠0）与反比例函数y2＝（k2≠0）的图象相交于A，B两点，其中点A的横坐标为1．当k1x＜时，x的取值范围是 0＜x＜1或x＜﹣1 ．
解：由正比例函数与反比例函数的对称性可得点B横坐标为﹣1，
由图象可得当k1x＜时，x的取值范围是0＜x＜1或x＜﹣1．
答案：0＜x＜1或x＜﹣1．
21．（2021•河北中考）用绘图软件绘制双曲线m：y＝与动直线l：y＝a，且交于一点，图1为a＝8时的视窗情形．
（1）当a＝15时，l与m的交点坐标为 （4，15） ；
（2）视窗的大小不变，但其可视范围可以变化，且变化前后原点O始终在视窗中心．
例如，为在视窗中看到（1）中的交点，可将图1中坐标系的单位长度变为原来的，其可视范围就由﹣15≤x≤15及﹣10≤y≤10变成了﹣30≤x≤30及﹣20≤y≤20（如图2）．当a＝﹣1.2和a＝﹣1.5时，l与m的交点分别是点A和B，为能看到m在A和B之间的一整段图象，需要将图1中坐标系的单位长度至少变为原来的，则整数k＝ 4 ．
解：（1）a＝15时，y＝15，
由得：，
答案：（4，15）；
（2）由得，
∴A（﹣50，﹣1.2），
由得，
∴B（﹣40，﹣1.5），
为能看到m在A（﹣50，﹣1.2）和B（﹣40，﹣1.5）之间的一整段图象，需要将图1中坐标系的单位长度至少变为原来的，
∴整数k＝4．
答案：4．
22．（2021•兰州中考）如图，一次函数y＝﹣x+b与反比例函数y＝﹣（x＞0）的图象分别交于点A（﹣2，m），B（4，n），与y轴交于点C，连接OA，OB．
（1）求一次函数y＝﹣x+b和反比例函数y＝（x＞0）的表达式；
（2）求△AOB的面积．
解：（1）∵点A在反比例函数y＝上，
∴﹣2m＝﹣10，
解得m＝5，
∴点A坐标为（﹣2，5）．
把（﹣2，5）代入y＝﹣x+b得5＝1+b，
解得b＝4，
∴一次函数表达式为y＝x+4，
把B（4，n）代入y＝x+4得n＝﹣2+4＝2，
∴点B坐标为（4，2），
∵点B在反比例函数y＝图象上，
∴k＝4×2＝8，
∴反比例函数表达式为y＝．
（2）把x＝0代入y＝x+4得y＝4，
∴点C坐标为（0，4），
∴S△AOB＝S△AOC+S△BOC＝×4×2+×4×4＝12．
四、反比例函数的应用
【高频考点精讲】
1．利用反比例函数解决实际问题
（1）能把实际的问题转化为数学问题，建立反比例函数的数学模型；
（2）注意在自变量和函数值的取值上的实际意义；
（3）问题中出现的不等关系转化成相等的关系来解，然后在作答中说明。
2．跨学科的反比例函数应用题
要熟练掌握物理或化学学科中的一些具有反比例函数关系的公式，同时体会数学中的转化思想。
3．反比例函数中的图表信息题
正确的认识图象，找到关键的点，运用好数形结合的思想。
【热点题型精练】
23．（2021•宜昌中考）某气球内充满了一定质量m的气体，当温度不变时，气球内气体的气压p（单位：kPa）是气体体积V（单位：m3）的反比例函数：p＝，能够反映两个变量p和V函数关系的图象是（ ）
A．B．
C．D．
解：∵气球内气体的气压p（单位：kPa）是气体体积V（单位：m3）的反比例函数：p＝（V，p都大于零），
∴能够反映两个变量p和V函数关系的图象是：．
答案：B．
24．（2021•青岛中考）车从甲地驶往乙地，行完全程所需的时间t（h）与行驶的平均速度v（km/h）之间的反比例函数关系如图所示．若列车要在2.5h内到达，则速度至少需要提高到 240 km/h．
解：∵从甲地驶往乙地的路程为200×3＝600（km），
∴汽车行驶完全程所需的时间t（h）与行驶的平均速度v（km/h）之间的关系式为t＝，
当t＝2.5h时，即2.5＝，
∴v＝240，
答：列车要在2.5h内到达，则速度至少需要提高到240km/h．
答案：240．
25．（2021•潍坊中考）某山村经过脱贫攻坚和乡村振兴，经济收入持续增长．经统计，近五年该村甲农户年度纯收入如表所示：
若记2016年度为第1年，在直角坐标系中用点（1，1.5），（2，2.5），（3，4.5），（4，7.5），（5，11.3）表示近五年甲农户纯收入的年度变化情况．如图所示，拟用下列三个函数模拟甲农户从2016年开始的年度纯收入变化趋势：y＝（m＞0），y＝kx+b（k＞0），y＝ax2﹣0.5x+c（a＞0），以便估算甲农户2021年度的纯收入．
（1）能否选用函数y＝（m＞0）进行模拟，请说明理由；
（2）你认为选用哪个函数模拟最合理，请说明理由；
（3）甲农户准备在2021年底购买一台价值16万元的农机设备，根据（2）中你选择的函数表达式，预测甲农户2021年度的纯收入能否满足购买农机设备的资金需求．
解：（1）∵1×1.5＝1.5，2×2.5＝5，
∴1.5≠5，
∴不能选用函数y＝（m＞0）进行模拟．
（2）选用y＝ax2﹣0.5x+c（a＞0），理由如下，
由（1）可知不能选用函数y＝（m＞0），
由（1，1.5），（2，2.5），（3，4.5），（4，7.5），（5，11.3）可知，
x每增大1个单位，y的变化不均匀，
∴不能选用函数y＝kx+b（k＞0），
故只能选用函数y＝ax2﹣0.5x+c（a＞0）模拟．
（3）把（1，1.5），（2，2.5）代入y＝ax2﹣0.5x+c（a＞0）得：
，解得：，
∴y＝0.5x2﹣0.5x+1.5，
当x＝6时，y＝0.5×36﹣0.5×6+1.5＝16.5，
∵16.5＞16，
∴甲农户2021年度的纯收入满足购买农机设备的资金需求．x
…
﹣4
﹣3
﹣2
﹣1
1
2
3
4
…
y
…
5
4
5
5
4
5
…
x
…
﹣3
﹣2
﹣1
0
1
2
3
4
…
y
…
﹣1

﹣3
0
3

1

.…
x
．．．
﹣3
﹣2
﹣1
0
1
2
3
4
．．．
y
．．．
﹣1
﹣3
0
3
1
．．．
年度（年）
2016
2017
2018
2019
2020
2021
年度纯收
入（万元）
1.5
2.5
4.5
7.5
11.3