2022年广东省深圳市龙岗区金稻田学校中考数学模拟试卷（四）

这是一份2022年广东省深圳市龙岗区金稻田学校中考数学模拟试卷（四），共21页。试卷主要包含了5)B，60，cs37∘≈0，【答案】B，【答案】D，【答案】C，【答案】A等内容，欢迎下载使用。
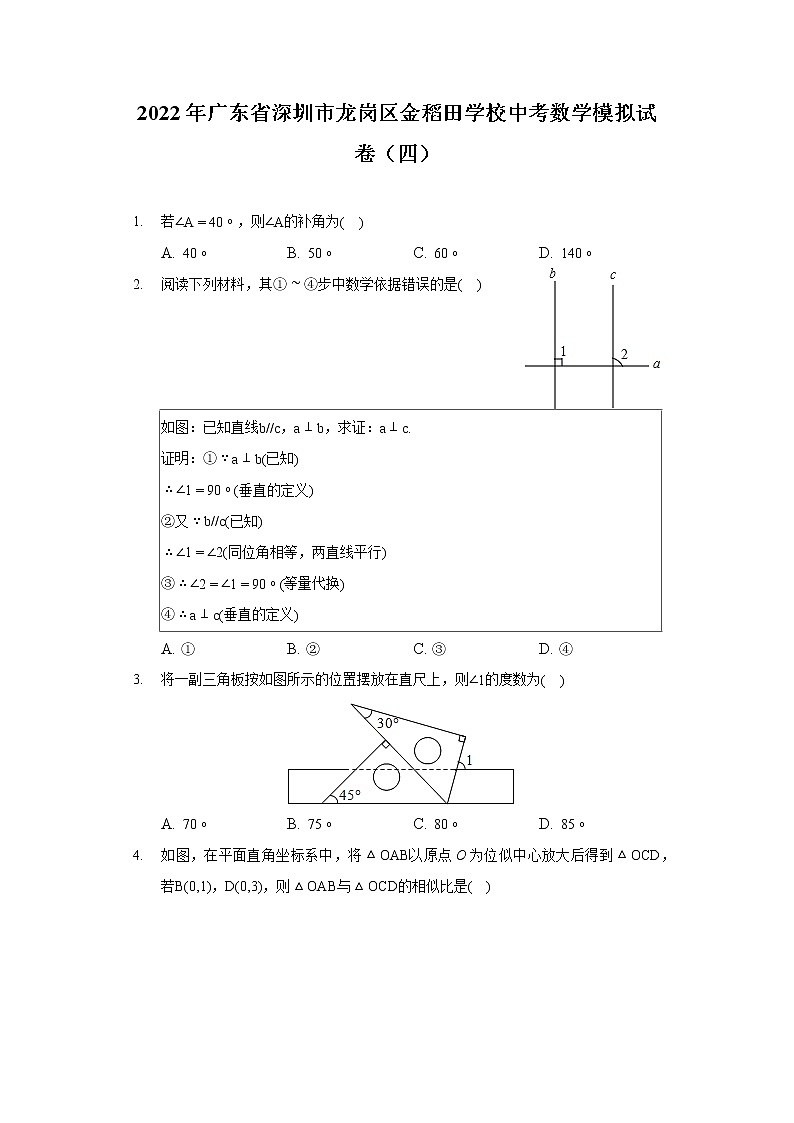
 2022年广东省深圳市龙岗区金稻田学校中考数学模拟试卷（四） 若，则的补角为A.  B.  C.  D. 阅读下列材料，其①④步中数学依据错误的是如图：已知直线，，求证：
证明：①已知
垂直的定义
②又已知
同位角相等，两直线平行
③等量代换
④垂直的定义A. ① B. ② C. ③ D. ④将一副三角板按如图所示的位置摆放在直尺上，则的度数为
A.  B.  C.  D. 如图，在平面直角坐标系中，将以原点O为位似中心放大后得到，若，，则与的相似比是
A. 2：1 B. 1：2 C. 3：1 D. 1：3如图，在中，AB的垂直平分线分别交AB、BC于点D、E，连接AE，若，，则BC的长是
A. 2 B. 4 C. 6 D. 8如图，≌，且点在AB边上，点恰好在BC的延长线上，下列结论错误的是
A.  B.
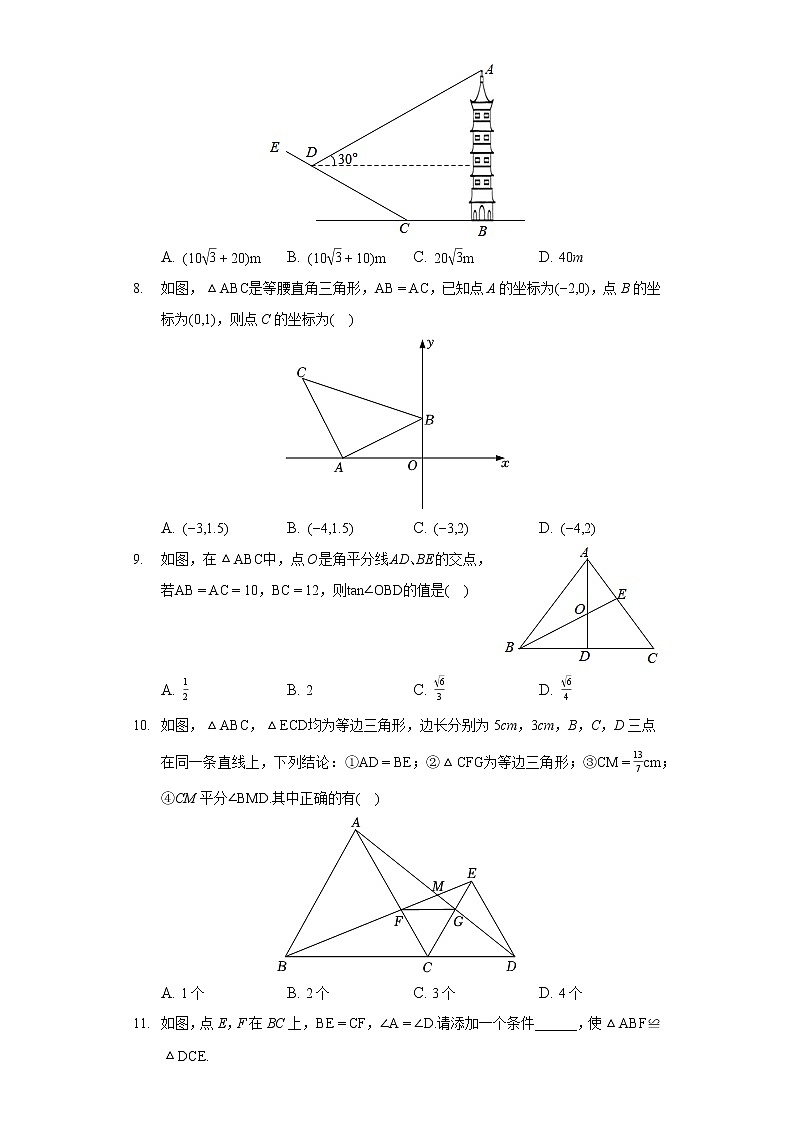
C.  D. 平分如图，在一次数学实践活动中，小明同学要测量一座与地面垂直的古塔AB的高度，他从古塔底部点B处前行30m到达斜坡CE的底部点C处，然后沿斜坡CE前行20m到达最佳测量点D处，在点D处测得塔顶A的仰角为，已知斜坡的斜面坡度：，且点A，B，C，D，E在同一平面内，小明同学测得古塔AB的高度是
A.  B.  C.  D. 40m如图，是等腰直角三角形，，已知点A的坐标为，点B的坐标为，则点C的坐标为
A.  B.  C.  D. 如图，在中，点O是角平分线AD、BE的交点，若，，则的值是

 A.  B. 2 C.  D. 如图，，均为等边三角形，边长分别为5cm，3cm，B，C，D三点在同一条直线上，下列结论：①；②为等边三角形；③；④CM平分其中正确的有
A. 1个 B. 2个 C. 3个 D. 4个如图，点E，F在BC上，，请添加一个条件______，使≌
如图，已知每个小方格的边长均为1，则与的周长比为______.


  如图，在中，，D，E分别是AB，BC的中点，连接AE，DE，若，，则点A到BC的距离是______.



  把两个含角的直角三角板按如图所示拼接在一起，点E为AD的中点，连结BE交AC于点则______.


  如图，，在OM上截取过点作，交ON于点，以点为圆心，为半径画弧，交OM于点；过点作，交ON于点，以点为圆心，为半径画弧，交OM于点；按此规律，所得线段的长等于______.
如图，，，点E在BC上，且求证：







 如图，在中，的平分线BD交AC边于点D，于点已知，
求证：；
若，求的面积.

  






 如图，某地政府为解决当地农户网络销售农特产品物流不畅问题，计划打通一条东西方向的隧道无人机从点A的正上方点C，沿正东方向以的速度飞行15s到达点D，测得A的俯角为，然后以同样的速度沿正东方向又飞行50s到达点E，测得点B的俯角为
求无人机的高度结果保留根号；
求AB的长度结果精确到
参考数据：，，，







 如图，在中，于点D，E为BD上一点，过点E作交AB于点F，过点F作分别交AD，AC于点N，G，过点G作交BC于点
求证：∽；
若，，设EF的长度为x，四边形EFGH的面积为y，求y与x之间的函数表达式，并求y的最大值．







 如图，和都是等腰直角三角形，，，，，D为BC边中点，连接AF，且A、F、E三点恰好在一条直线上，EF交BC于点H，连接BF，
求证：；
猜想CE，BF，BC之间的数量关系，并证明；
若，，请直接写出线段AC，AE的长.








答案和解析 1.【答案】D
 【解析】解：因为，
所以的补角为：
故选：
根据互补两角的和为，即可求出的补角的度数．
本题考查了补角的知识．掌握互为补角的两角之和为180度是解题的关键．
 2.【答案】B
 【解析】证明：①已知，
垂直的定义，
②又已知，
两直线平行，同位角相等，
③等量代换，
④垂直的定义，
①④步中数学依据错误的是②，
故选：
根据垂直的定义得到，再根据两直线平行，同位角相等得到，即可判定
此题考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解题的关键．
 3.【答案】B
 【解析】解：如图，

，
，
，
，
故选：
利用三角形内角和定理和平行线的性质解题即可．
此题考查平行线的性质，关键是根据两直线平行，同位角相等解答．
 4.【答案】D
 【解析】解：，
，
以原点O为位似中心放大后得到
与的相似比是OB：：
故选：
根据信息，找到OB与OD的比值即可．
本题考查位似变换、坐标与图形的性质．关键在于找到相似比就是对应边的比．
 5.【答案】C
 【解析】解：是AB的垂直平分线，，
，
，
故选：
根据线段的垂直平分线的性质得到，结合图形计算，得到答案．
本题考查的是线段的垂直平分线的性质，解题的关键是掌握线段的垂直平分线上的点到线段的两个端点的距离相等．
 6.【答案】C
 【解析】解：≌，
，，，
A.，
，
，故本选项不符合题意；
B.，
，
，
，
，故本选项不符合题意；
C.不能推出，故本选项符合题意；
D.，，
，
即平分，故本选项不符合题意；
故选：
根据全等三角形的性质得出，，，再逐个判断即可．
本题考查了全等三角形的性质定理，能熟记全等三角形的性质全等三角形的对应角相等，对应边相等是解此题的关键．
 7.【答案】A
 【解析】解：过D作于F，于H，
，，
斜坡的斜面坡度：，
：，
设，，
，
，
，，
，
，
，
，
故选：
过D作于F，于H，得到，，设，，根据勾股定理得到，求得，，，于是得到结论．
本题考查了解直角三角形的应用-仰角俯角问题，解直角三角形的应用-坡角坡度问题，正确的作出辅助线构造直角三角形是解题的关键．
 8.【答案】C
 【解析】解：过C作轴于D，则，

是等腰直角三角形，
，
又，
，，
，
在和中，
，
≌，
，，
又点A的坐标为，点B的坐标为，
，，
，
又点C在第三象限，
点C的坐标为
故选：
先根据AAS判定≌，得出，，再根据点A的坐标为，点B的坐标为，求得CD和OD的长，得出点C的坐标．
本题主要考查了等腰直角三角形的性质，全等三角形的判定与性质，解决问题的关键是根据全等三角形的性质，求得点C到坐标轴的距离．
 9.【答案】A
 【解析】解：如图：

作于F，
，AD平分

根据勾股定理得：
平分
，，
设，则，在中，根据勾股定理得：



在中，
故选：
放在中利用三角函数定义即可求．
本题考查勾股定理，角平分线性质及锐角三角函数的定义，构造直角三角形求线段的长是求解本题的关键．
 10.【答案】C
 【解析】解：，均为等边三角形，
，，，
，
在和中，
，
≌，
，故①正确；
，
在和中，
，
≌，
，
，
为等边三角形，故②正确；

，
、F、C、G四点共圆，
，，
，
平分，故④正确；
过点E作，则，
，
，
，
，，
∽
，
，
故③错误．
故选：
根据等边三角形的性质得，，，，则，利用“SAS”可判断≌，则，可判断①；
由等边三角形的判定得出是等边三角形，可判断②；
证明∽，求出CM长，可判断③；
证明M、F、C、G四点共圆，由圆周角定理得出，，得出，所以CM平分，可判断④．
本题考查全等三角形、相似三角形综合，熟练掌握全等三角形的手拉手模型是解题关键．
 11.【答案】
 【解析】解：，
，
，
添加，
在和中，
，
≌，
故答案为：
求出，再根据全等三角形的判定定理判断即可．
本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键．
 12.【答案】2：1
 【解析】解：如图，

分别过点A、点E作，，垂足分别为点M、N，
则，
，，，，
，
∽，
，，
，
，
又，
∽，
与的周长之比为2：
故答案为：2：
根据题意构造直角三角形并根据其各边的长度证明∽，从而推出，再利用平行线的性质得到，进而推出∽，则两三角形的周长之比就是两三角形的相似比．
本题考查相似三角形的判定与性质，解题的关键是通过构造直角三角形推出，再利用相似三角形的性质求解．
 13.【答案】
 【解析】解：设点A到BC的距离是h，
在中，，E是BC的中点，，
，
，E分别是AB，BC的中点，，
，
由勾股定理得：，
则，
解得：，
故答案为：
根据直角三角形的性质求出BC，根据三角形中位线定理求出AC，根据勾股定理求出AB，根据三角形的面积公式计算，得到答案．
本题考查的是三角形中位线定理、直角三角形的性质、勾股定理、三角形的面积计算，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
 14.【答案】
 【解析】解：连接CE，，，E是AD的中点，
，，

，，
，，
，
∽，
，
，

故答案为
连接CE，根据直角三角形的性质，用AD表示AB，CE，再证明得∽，由相似三角形的性质得，进而得便可．
本题主要考查了直角三角形的性质，相似三角形的性质与判定，关键是证明三角形相似．
 15.【答案】
 【解析】解：，，
，
，，
，
，
，
同法可得，…，
由此规律可得，
，
，
故答案为
利用三角形中位线定理证明，，寻找规律解决问题即可．
本题考查解直角三角形，规律型问题，解题的关键是学会探究规律的方法，属于中考常考题型．
 16.【答案】证明：，
，
在和中，
，
≌，

 【解析】先根据平行线的性质得到，然后根据“SAS”可判断≌，从而根据全等三角形的性质得到结论．
本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
 17.【答案】证明：平分，，
，
，
，
，
；
解：由题意得，，，
，

 【解析】计算出和，利用等角对等边即可证明；
利用锐角三角函数求出BC即可计算的面积．
本题考查等腰三角形的判定以及利用锐角三角函数求值，解题的关键是求出和的度数．
 18.【答案】解：由题意，，
在中，，
，
答：无人机的高度AC是米；

过点B作于点F，则四边形ABFC是矩形，
，，
在中，，
，
，
米，
答：隧道AB的长度约为243米．
 【解析】利用正切函数即可求出AC的长；
过点B作于点F，则四边形ABFC是矩形，得到，，在中利用正切函数即可求得EF，进而即可求得米．
本题考查了解直角三角形的应用--仰角俯角问题，要求学生能借助俯角构造直角三角形并解直角三角形．注意方程思想与数形结合思想的应用．
 19.【答案】证明：，，
▱EFGH为矩形，
，
，
，
∽；
解：，，
，，
，
又，，
，
四边形EFGH，EFND都是矩形，
，，
，，
，

由得∽，
，即，
，
，


，
当时，y取得最大值，最大值为
 【解析】利用平行，垂直关系，判定四边形EFHG为矩形，再根据平行关系判定角度相等，进而判定三角形相似；
利用相似三角形的判定和二次函数极值的求解，找到相似三角形，找出函数表达式，求出极值，即可解决问题．
本题考查了相似三角形的判定和二次函数极值的求解，解题关键是找到相似三角形，找出函数表达式．
 20.【答案】证明：连接
，，，
，
，
，
，
≌，


结论：
理由：，都是等腰直角三角形，
，，
≌，
，，
，
，
，
，，
≌，
，
，
，


解：设
，，
∽，
，
，
，
，
在中，，
，
，
或舍弃，
，
，

 【解析】连接AD，证明≌，可得
结论：利用全等三角形的性质证明，再证明，可得结论．
设证明∽，可得，推出，推出，，在中，根据，构建方程求出m即可解决问题．
本题属于三角形综合题，考查了等腰直角三角形的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理等知识，解题的关键是证明≌，≌，∽