数学八年级下册18.2.3 正方形同步达标检测题

这是一份数学八年级下册18.2.3 正方形同步达标检测题，共13页。
B.添加“AB//CD”，则四边形ABCD是菱形
C.添加“OA=OC”，则四边形ABCD是菱形
D.添加“∠ABC=∠BCD=90∘”，则四边形ABCD是正方形
2. 将图1中两个三角形按图2所示的方式摆放，其中四边形ABCD为矩形，分别连接PQ，MN，甲、乙两人有如下结论：
甲：若四边形ABCD为正方形，则四边形PQMN必是正方形；
乙：若四边形PQMN为正方形，则四边形ABCD必是正方形．
下列判断正确的是( )

A.甲正确，乙不正确B.甲不正确，乙正确
C.甲、乙都不正确D.甲、乙都正确
3. 如图，在△ABC中，点E，D，F分别在边AB，BC，CA上，且DE // CA，DF // BA，下列四个判断中，不正确的是( )

A.四边形AEDF是平行四边形
B.如果AD=EF，那么四边形AEDF是矩形
C.如果AD平分∠EAF，那么四边形AEDF是菱形
D.如果AD⊥BC且AB=AC，那么四边形AEDF是正方形
4. 在一次数学课上，张老师出示了一个题目：“如图，▱ABCD的对角线相交于点O，过点O作EF垂直于BD交AB，CD分别于点F，E，连接DF，BE．请根据上述条件，写出一个正确结论．”其中四位同学写出的结论如下：
小青：OE=OF；小何：四边形DFBE是正方形；
小夏：S四边形AFED=S四边形FBCE；小雨：∠ACE=∠CAF．
这四位同学写出的结论中不正确的是( )

A.小青B.小何C.小夏D.小雨

5. 如图所示，在正方形ABCD中，G为CD边中点，连接AG并延长线于E点，对角线BD交AG于F点，已知FG=2，则线段AE的长度为（ ）
A.6B.8C.10D.12
6. 如图，在矩形ABCD中，∠ADC的平分线于AB交于E，点F在DE的延长线上，∠BFE=90∘，连接AF，CF，CF与AB交于G，有以下结论：
①AE=BC ②AF=CF ③BF2=FG⋅FC ④EG⋅AE=BG⋅AB
其中正确的个数是（ ）
A.1B.2C.3D.4
7. 矩形ABCD与CEFG如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH，若BC=EF=2,CD=CE=1，则GH=（ ）
A.1B.23C.22D.52

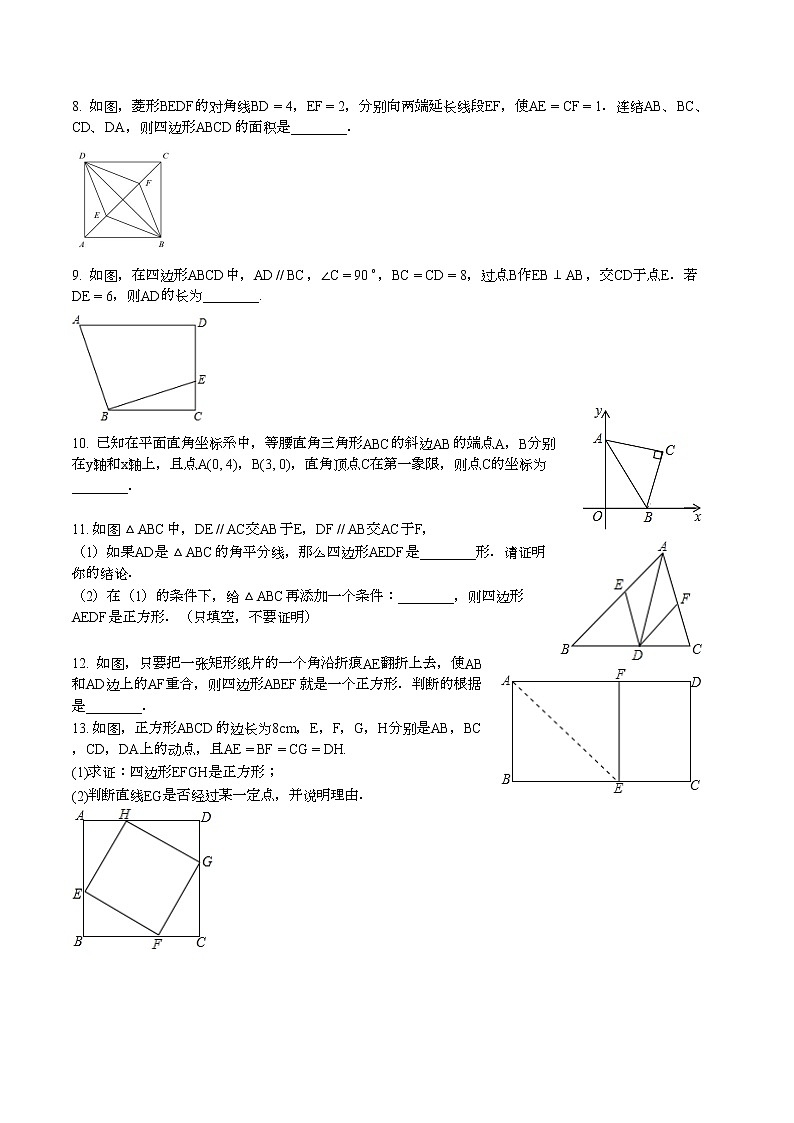
8. 如图，菱形BEDF的对角线BD=4，EF=2，分别向两端延长线段EF，使AE=CF=1．连结AB、BC、CD、DA，则四边形ABCD的面积是________．

9. 如图，在四边形ABCD中，AD // BC，∠C=90∘，BC=CD=8，过点B作EB⊥AB，交CD于点E．若DE=6，则AD的长为________.

10. 已知在平面直角坐标系中，等腰直角三角形ABC的斜边AB的端点A，B分别在y轴和x轴上，且点A(0, 4)，B(3, 0)，直角顶点C在第一象限，则点C的坐标为________．

11. 如图△ABC中，DE // AC交AB于E，DF // AB交AC于F，
（1）如果AD是△ABC的角平分线，那么四边形AEDF是________形．请证明你的结论．
（2）在（1）的条件下，给△ABC再添加一个条件：________，则四边形AEDF是正方形．（只填空，不要证明）

12. 如图，只要把一张矩形纸片的一个角沿折痕AE翻折上去，使AB和AD边上的AF重合，则四边形ABEF就是一个正方形．判断的根据是________．
13. 如图，正方形ABCD的边长为8cm，E，F，G，H分别是AB，BC，CD，DA上的动点，且AE=BF=CG=DH.
(1)求证：四边形EFGH是正方形；
(2)判断直线EG是否经过某一定点，并说明理由．

14. 如图，四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交BC于点F，以DE，EF为邻边作矩形DEFG，连接CG.
(1)求证：矩形DEFG是正方形；
(2)若AB=22，CE=2，求CG的长；
(3)当∠ADE=40∘时，求∠EFC的度数.

15. 在8×6的正方形网格中，正方形边长为1单位，△ABC的三个顶点均在格点上，请用无刻度的直尺作图．

（1）在图1中画一个与△ABC面积相等，且以BC为边的平行四边形，顶点均在格点上；
（2）在图2中画一个以点C为顶点的正方形，其余三点均在格点上，此正方形的面积与△ABC面积相等．

16. 已知：如图，E是正方形ABCD的对角线BD上的点，连接AE，CE．
(1)求证：AE=CE；
(2)若将△ABE沿AB对折后得到△ABF；当点E在BD的何处时，四边形AFBE是正方形？请证明你的结论．

17. 如图1，E是▱ABCD边AB上的一点，连接CE，以CE为边作▱CEGF 使点D在线段GF上（不与端点重合）．
(1)求证： ∠CDF=∠CEB；
(2)如图2，连接AG，当点E是AB中点且AG=AE时，求证：四边形CEGF是矩形；
(3)在(2)的情况下，当AB=AD且∠DAB=90∘时，判断线段DG和DF的数量关系，并证明．

18. 在▱ABCD中，∠ABC的平分线交AD于点E，交CD的延长线于点F，分别过点E，F作EG//DF，GF//AD.

(1)如图1，求证：四边形EDFG是菱形；
(2)如图2，连接AG，DG，DG与EF相交于点O，若∠AGD=90∘，求证：AD=2AB；
(3)如图3，连接DG交EF于点O，连接OC，若∠ABC=90∘，AB=6，BC=10，直接写出OC的长．
参考答案与试题解析
一、 选择题
1.
【答案】
A
2.
【答案】
B
3.
【答案】
D
4.
【答案】
B
5.
【答案】
D
6.
【答案】
C
7.
【答案】
C
二、 填空题
8.
【答案】
8
9.
【答案】
10
10.
【答案】
(3.5, 3.5)
11.
【答案】
（1）菱形，
证明：∵ DE // AF，DF // AE，
∴ 四边形AEDF是平行四边形．
∵ DE // AC
∴ ∠1=∠3
又∵ ∠1=∠2∘
∴ ∠2=∠3
∴ AE=ED
∴ □AEDF是菱形；
（2）∠BAC=90∘，
理由如下：∵ 四边形AEDF是菱形，∠BAC=90∘，
∴ 四边形AEDF是正方形．
12.
【答案】
有一组邻边相等的矩形是正方形
三、 解答题
13.
【答案】
(1)证明：∵ ∠BAD=∠ABC=∠BCD=∠CDA=90∘，
AB=BC=CD=DA，
∵ AE=BF=CG=DH，
∴ AH=BE=CF=DG，
∴ △EAH≅△FBE≅△GCF≅△HDG，
∴ EH=EF=FG=HG，∠AEH=∠BFE，
∴ 四边形EFGH是菱形．
∴ ∠BEF+∠BFE=90∘，∠AEH=∠BFE，
∴ ∠BEF+∠AEH=90∘，
∴ ∠HEF=90∘，
∵ 四边形EFGH是菱形，∠HEF=90∘，
∴ 四边形EFGH是正方形．
(2)解：直线EG经过正方形ABCD的中心，理由如下：
连接BD交EG于点O．
∵ 四边形ABCD是正方形．
∴ AB//DC，
∴ ∠EBD=∠GDB，
∵ ∠EOB=∠GOD，∠EBD=∠GDB，BE=DG，
∴ △EOB≅△GOD，
∴ BO=DO，即点O为BD的中点．
∴ 直线EG经过正方形ABCD的中心．
14.
【答案】
(1)证明：过点E作EP⊥CD于P，EQ⊥BC于Q，如图，
∵ 四边形ABCD为正方形，
∴∠DCA=∠BCA=45∘.
∵EP⊥CD，EQ⊥BC，
∴∠QEC=∠PEC=45∘，EQ=EP.
∵ ∠QEF+∠FEC=45∘，∠PED+∠FEC=45∘，
∴ ∠QEF=∠PED.
在Rt△EQF和Rt△EPD中，
∠QEF=∠PED，EQ=EP，∠EQF=∠EPD，
∴ Rt△EQF≅Rt△EPD(ASA)，
∴ EF=ED，
∴ 矩形DEFG是正方形.
(2)解：如图2，
在Rt△ABC中，AC=2AB=4，
∵ CE=2，
∴ AE=CE，
∴ 点F与C重合，此时△DCG是等腰直角三角形，
∴CG=2.
(3)解：当∠ADE=40∘时，
∠DEC=45∘+40∘=85∘，
∵ ∠DEF=90∘，
∴ ∠CEF=5∘.
∵ ∠ECF=45∘，
∴ ∠EFC=130∘，
15.
【答案】
如图1所示：平行四边形BCFE即为所求；
如图2所示：正方形CDEF即为所求．
16.
【答案】
(1)证明：∵ 四边形ABCD是正方形，
∴ AB=CB，∠BAD=∠ABC=90∘，
∠ABE=∠CBE=45∘，
在△ABE和△CBE中，
AB=CB，∠ABE=∠CBE，BE=BE，
∴ △ABE≅△CBE(SAS)，
∴ AE=CE．
(2)解：点E在BD的中点时，四边形AFBE是正方形.
理由如下：
由折叠的性质得：∠F=∠AEB，
AF=AE，BF=BE，
∵ ∠BAD=90∘，E是BD的中点，
∴ AE=12BD=BE=DE，
∵ AE=CE，
∴ AE=BE=CE=DE=AF=BF，
∴ 四边形AFBE是菱形，E是正方形ABCD对角线的交点，
∴ AE⊥BD，
∴ ∠AEB=90∘，
∴ 四边形AFBE是正方形．
17.
【答案】
(1)证明：∵ 四边形ABCD与四边形CEGF是平行四边形，
∴ AB//CD,CE//FG，
∴ ∠BEC=∠DCE，∠DCE=∠CDF，
∴ ∠CDF=∠CEB.
(2)证明：延长FG，BA交于点H．
∵ 四边形ABCD是平行四边形，
∴ AB=CD，
∵ E是AB中点，
∴ AE=12AB=12CD .
∵ AB//CD，CE//FG，
∴ 四边形CDHE是平行四边形，
∴ HE=CD，
∴ AE=12HE，
∴ AH=12HE=AE．
∵ AG=AE，
∴ ∠AGE=∠AEG ，AG=AH，
∴ ∠H=∠AGH ．
在△EGH中，∠H+∠HEG+∠HGE=180∘，
即∠H+∠AGH+∠AGE+∠AEG=180∘，
∴ ∠HGE=∠AGH+∠AGE=90∘，
∴ ∠EGF=90∘，
∵ 四边形CEGF是平行四边形，
∴ 平行四边形CEGF是矩形．
(3)解：DG=32DF，理由如下：
连接DE，设AE=a，
∵ AB=AD，∠DAB=90∘，
四边形ABCD为平行四边形，
∴ 平行四边形ABCD是正方形，
∴ BC=AB=AD=2a，EB=a， ∠B=90∘，
在Rt△ADE和Rt△BCE中，
DE=AD2+AE2=5a，
CE=BE2+BC2=5a，
∵ 四边形CEGF是矩形，
∴ GF=CE=5a，∠EGF=90∘，
由(1)得，在平行四边CDHE中，
EH=CD=2a，DH=CE=5a．
S△DHE=12AD⋅HE=12EG⋅DH，
∴ EG=AD⋅HEDH=455a ，
在Rt△EDG中，DG=ED2−DG2=355a，
∴ DF=GF−DG=255a，
∴ DG=32DF.
18.
【答案】
(1)证明：∵EG//DF，GF//AD，
∴四边形EDFG是平行四边形．
∵AB//CD，∴∠ABF=∠CFB.
∵AD//BC，∴∠CBF=∠DEF.
∵BF平分∠ABC，∴∠ABF=∠CBF，
∴∠DEF=∠CFB，∴DE=DF，
∴四边形EDFG是菱形．
(2)证明：由(1)知四边形EDFG是菱形，
∴∠BOD=90∘，GF//AD．
∵∠AGD=90∘，
∴AG//BF，
∴四边形AEFG是平行四边形，
∴AE=GF．
∵GF=DE，
∴AD=2AE．
∵AD//BC，
∴∠CBF=∠AEB．
∵∠ABE=∠CBF，
∴∠ABE=∠AEB，
∴AB=AE，
∴AD=2AB．
(3)解：∵∠ABC=90∘，
∴四边形ABCD是矩形，
∴∠ADC=90∘，
∴∠EDF=90∘，
∴菱形EDFG是正方形，
∴∠CBF=45∘.
∵∠FCB=90∘，
∴∠CFB=45∘，
∴∠CBF=∠CFB，
∴BC=CF=10．
同理，AB=AE=6，则ED=4.
如图，过点O作ON⊥DF于点N，
则ON=DN=2，
∴CN=6+2=8，
∴OC=ON2+CN2=22+82=217．