
2022年北京市朝阳区中考数学模拟试卷(2)(word版含答案)
展开2022年北京市朝阳区中考数学模拟试卷(2)
一.选择题(共8小题,满分16分,每小题2分)
1.(2分)若式子有意义,则x的取值范围是( )
A.x≥﹣ B.x≥﹣2 C.x≠﹣2 D.x≠﹣
2.(2分)根据测试,华为首款5G手机传输1M的文件只需0.0025秒,其中0.0025用科学记数法表示为( )
A.2.5×10﹣3 B.2.5×10﹣4 C.25×10﹣4 D.0.25×10﹣2
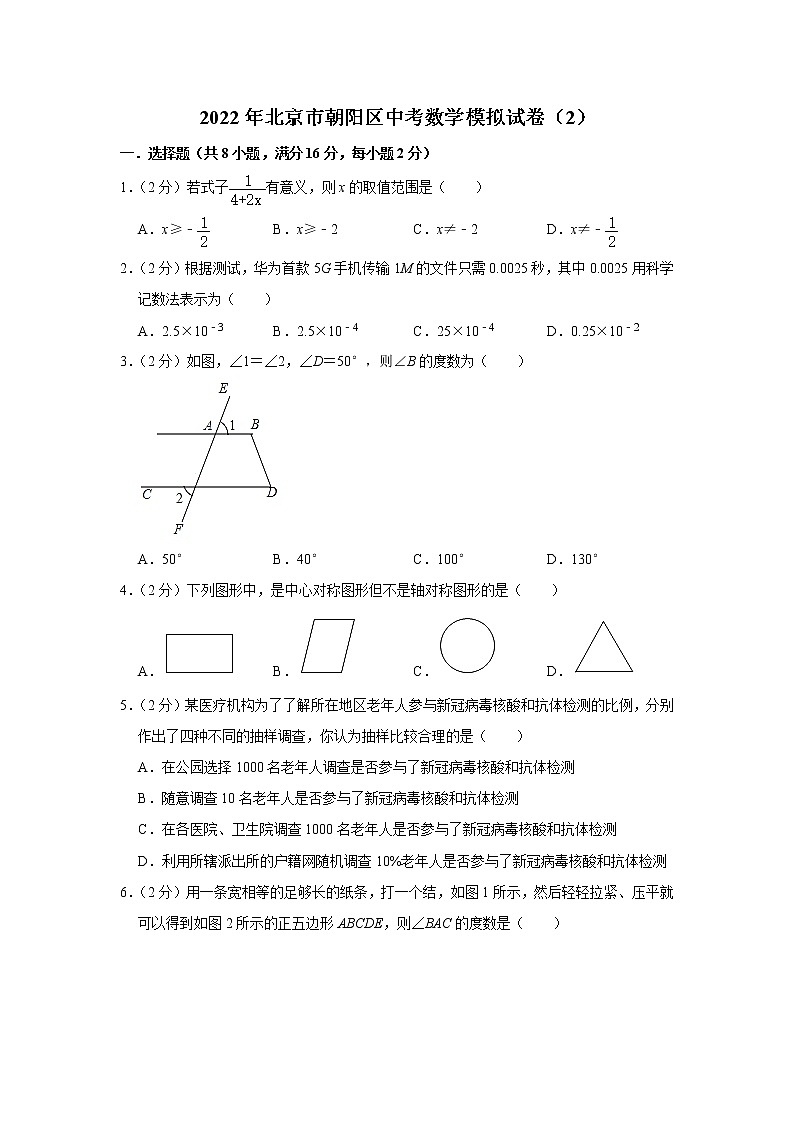
3.(2分)如图,∠1=∠2,∠D=50°,则∠B的度数为( )
A.50° B.40° C.100° D.130°
4.(2分)下列图形中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
5.(2分)某医疗机构为了了解所在地区老年人参与新冠病毒核酸和抗体检测的比例,分别作出了四种不同的抽样调查,你认为抽样比较合理的是( )
A.在公园选择1000名老年人调查是否参与了新冠病毒核酸和抗体检测
B.随意调查10名老年人是否参与了新冠病毒核酸和抗体检测
C.在各医院、卫生院调查1000名老年人是否参与了新冠病毒核酸和抗体检测
D.利用所辖派出所的户籍网随机调查10%老年人是否参与了新冠病毒核酸和抗体检测
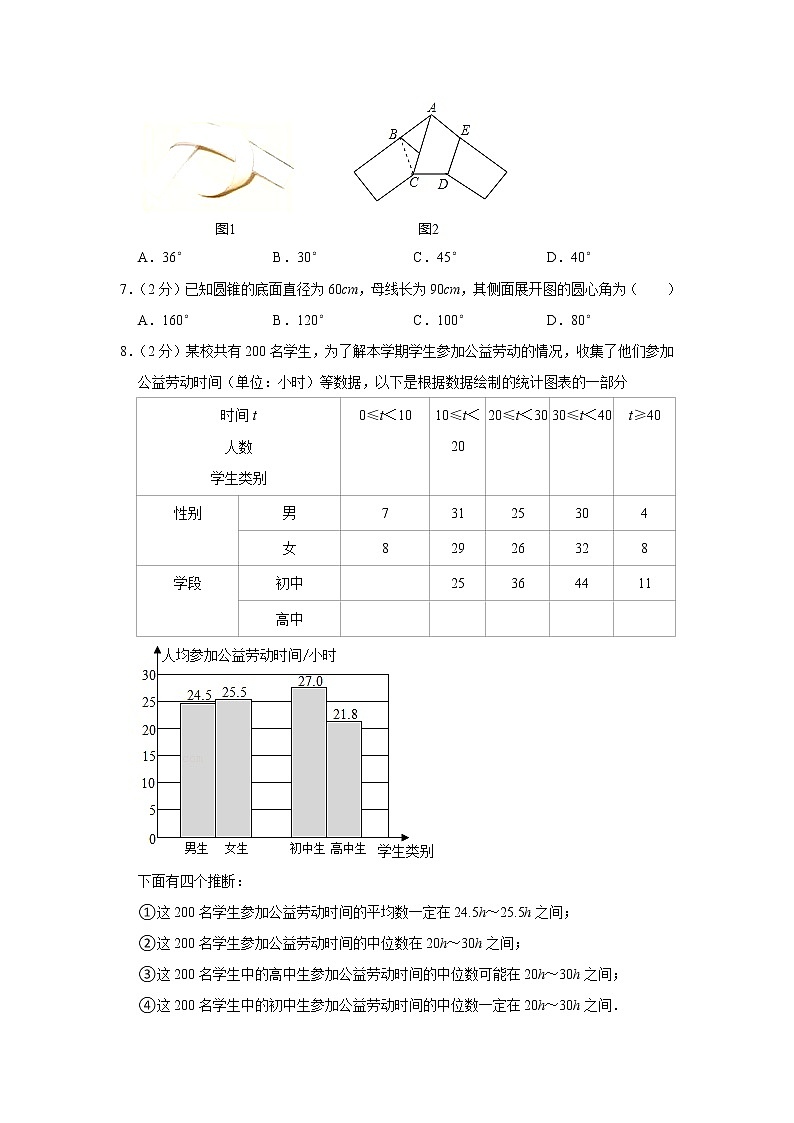
6.(2分)用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE,则∠BAC的度数是( )
A.36° B.30° C.45° D.40°
7.(2分)已知圆锥的底面直径为60cm,母线长为90cm,其侧面展开图的圆心角为( )
A.160° B.120° C.100° D.80°
8.(2分)某校共有200名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:小时)等数据,以下是根据数据绘制的统计图表的一部分
时间t
人数
学生类别
0≤t<10
10≤t<20
20≤t<30
30≤t<40
t≥40
性别
男
7
31
25
30
4
女
8
29
26
32
8
学段
初中
25
36
44
11
高中
下面有四个推断:
①这200名学生参加公益劳动时间的平均数一定在24.5h~25.5h之间;
②这200名学生参加公益劳动时间的中位数在20h~30h之间;
③这200名学生中的高中生参加公益劳动时间的中位数可能在20h~30h之间;
④这200名学生中的初中生参加公益劳动时间的中位数一定在20h~30h之间.
所有合理推断的序号是( )
A.①②③④ B.①②④ C.①②③ D.①④
二.填空题(共8小题,满分16分,每小题2分)
9.(2分)只有 不同的两个数叫互为相反数.0的相反数是 ,1的相反数是 .
10.(2分)分解因式:x3﹣xy2= .
11.(2分)在一个不透明的盒子中,装有除颜色外完全相同的乒乓球共24个,从中随机摸出一个乒乓球,若摸到黄色乒乓球的概率为,该盒子中装有黄色乒乓球的个数是 .
12.(2分)如图,△ABC内接于⊙O,若∠AOB=110°,则∠C= 度.
13.(2分)某型号飞机的机翼形状如图所示,根据图中数据计算AB的长为 m.(结果保留根号)
14.(2分)将直线y=2x向下平移3个单位长度后,得到的直线经过点(m+2,﹣5),则m的值为 .
15.(2分)用一个a的值说明命题“若a2>1,则a>1”是假命题,这个值可以是a= .
16.(2分)上学期学校举办了“SD杯古诗词”竞赛.小宇、小尧、小非三位同学进入了最后冠军的角逐.决
赛共分六轮,规定:每轮分别决出第1,2,3名(不并列),对应名次的得分都分别为a,b,c(a>b>c且a,b,c均为正整数);选手最后得分为各轮得分之和,得分最高者为冠军.
下表是三位选手在每轮比赛中的部分得分情况,根据题中所给信息,
第一轮
第二轮
第三轮
第四轮
第五轮
第六轮
最后得分
小宇
a
a
26
小尧
a
b
c
11
小非
b
b
11
判断下列说法一定错误的是 .(填序号)
①小宇可能有一轮比赛获第二名;
②小尧有三轮比赛获第三名;
③小非可能有一轮比赛获第一名;
④每轮比赛第一名得分a为5.
三.解答题(共12小题,满分68分)
17.(5分)计算:|﹣2|﹣(π﹣2019)0+()﹣2﹣2sin60°+.
18.(5分)解下列不等式,并把解在数轴上表示出来.
(1)5x﹣5<2(2+x);
(2)>1;
(3);
(4)x(x+4)≤(x+1)2+9.
19.(5分)(1)计算:
(2)计算:
(3)先化简,再求值:
已知=3,求的值.
20.(5分)如图,已知△ABC中,∠ACB=60°,BC<AB<AC.
(1)求作∠PBC,使得∠PBC=30°且点P在AC上;
(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若AB=4,∠A=45°,求AC的长度.
21.(5分)已知关于x的一元二次方程x2+(m+2)x+2m=0.
(1)求证:方程总有两个实数根;
(2)若该方程有一个根大于3,求m的取值范围.
22.(5分)如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、作CE∥BD,DE∥AC,CE和DE交于点E
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=10时,求CE和AE的长.
23.(6分)如图,一次函数y=kx+b的图象交反比例函数y=的图象于A(2,﹣4),B(a,﹣1)两点.
(1)求反比例函数与一次函数解析式.
(2)连接OA,OB,求△OAB的面积.
(3)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?
24.(6分)如图,⊙O与△ABC的AC边相切于点C,与BC边交于点E,⊙O过AB上一点D,且DE∥AO,CE是⊙O的直径.
(1)求证:AB是⊙O的切线;
(2)若BD=4,EC=6,求AC的长.
25.(6分)为全力抗击疫情,响应政府“停课不停学”的号召,某市教育局发布关于疫情防控期间开展在线课程教学的通知:从2月10日开始,全市初高中毕业班按照教学计划,开展在线课程教学和答疑,据互联网后台数据显示,某中学九年级七科老师3月5日在线答疑问题各学科个数如下表:
学科
语文
数学
英语
物理
化学
道德与法治
历史
数量/个
27
28
28
26
23
21
22
(1)直接写出九年级七科老师3月5日在线答疑问题各学科个数的众数与中位数;
(2)计算九年级七科老师在线答疑问题各学科个数的平均数.
26.(6分)如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.
(1)求证:△FAC≌△BAE;
(2)图中可以通过旋转△BAE而得到△FAC,请你说出旋转中心、旋转方向和旋转角的度数.
27.(7分)已知二次函数y=ax2﹣2ax﹣2图象经过点P(﹣1,1).
(1)求a的值和图象的顶点坐标;
(2)若点Q(m,n)在该二次函数图象上,当﹣1≤m<4时,请根据图象直接写出n的取值范围.
28.(7分)如图,在等腰直角△ABC中,∠B=90°,AB=BC=4.动点P以每秒2个单位长度的速度沿射线AB运动,过点P作PF⊥AC于点F,以AF,AP为邻边作▱FAPG;▱FAPG与等腰直角△ABC的重叠部分面积为y(平方单位),y>0,点F与点C重合时运动停止,设点P的运动时间为x秒.
(1)直接写出点G落在BC边上时x的值.
(2)求y与x的函数关系式.
(3)直接写出点G与△ABC各顶点的连线平分△ABC面积时x的值.
2022年北京市朝阳区中考数学模拟试卷(2)
参考答案与试题解析
一.选择题(共8小题,满分16分,每小题2分)
1.(2分)若式子有意义,则x的取值范围是( )
A.x≥﹣ B.x≥﹣2 C.x≠﹣2 D.x≠﹣
【解答】解:∵式子有意义,
∴4+2x≠0.
解得:x≠﹣2.
故选:C.
2.(2分)根据测试,华为首款5G手机传输1M的文件只需0.0025秒,其中0.0025用科学记数法表示为( )
A.2.5×10﹣3 B.2.5×10﹣4 C.25×10﹣4 D.0.25×10﹣2
【解答】解:0.0025用科学记数法表示为2.5×10﹣3.
故选:A.
3.(2分)如图,∠1=∠2,∠D=50°,则∠B的度数为( )
A.50° B.40° C.100° D.130°
【解答】解:如图所示:
∵∠1=∠2,∠1=∠3,
∴∠2=∠3,
∴AB∥CD,
∴∠B+∠D=180°,
又∵∠D=50°,
∴∠B=130°,
故选:D.
4.(2分)下列图形中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
【解答】解:A、既是中心对称图形,又是轴对称图形,故本选项不合题意;
B、是中心对称图形,但不是轴对称图形,故本选项符合题意;
C、既是中心对称图形,又是轴对称图形,故本选项不合题意;
D、不是中心对称图形,是轴对称图形,故本选项不合题意;
故选:B.
5.(2分)某医疗机构为了了解所在地区老年人参与新冠病毒核酸和抗体检测的比例,分别作出了四种不同的抽样调查,你认为抽样比较合理的是( )
A.在公园选择1000名老年人调查是否参与了新冠病毒核酸和抗体检测
B.随意调查10名老年人是否参与了新冠病毒核酸和抗体检测
C.在各医院、卫生院调查1000名老年人是否参与了新冠病毒核酸和抗体检测
D.利用所辖派出所的户籍网随机调查10%老年人是否参与了新冠病毒核酸和抗体检测
【解答】解:在公园、医院、卫生院选择老人调查,样本不具有代表性,故选项A、C抽样不合理;
随机调查10人,样本容量太小,不具有代表性,故选项B抽样不合理;
利用所辖派出所的户籍网随机调查10%老年人进行调查,抽样具有随机性和代表性,抽样合理.
故选:D.
6.(2分)用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE,则∠BAC的度数是( )
A.36° B.30° C.45° D.40°
【解答】解:因为正五边形的每个内角都相等,边长相等,
所以∠ABC==108°,
∵正五边形的每个条边相等,
∴△ABC是等腰三角形,
∴∠BAC=∠BCA,
∴∠BAC=(180°﹣108°)÷2=36°.
故选:A.
7.(2分)已知圆锥的底面直径为60cm,母线长为90cm,其侧面展开图的圆心角为( )
A.160° B.120° C.100° D.80°
【解答】解:设圆心角为n°.
由题意:圆锥的底面的周长=展开图扇形的弧长,
∴60π=,
解得n=120°,
故选:B.
8.(2分)某校共有200名学生,为了解本学期学生参加公益劳动的情况,收集了他们参加公益劳动时间(单位:小时)等数据,以下是根据数据绘制的统计图表的一部分
时间t
人数
学生类别
0≤t<10
10≤t<20
20≤t<30
30≤t<40
t≥40
性别
男
7
31
25
30
4
女
8
29
26
32
8
学段
初中
25
36
44
11
高中
下面有四个推断:
①这200名学生参加公益劳动时间的平均数一定在24.5h~25.5h之间;
②这200名学生参加公益劳动时间的中位数在20h~30h之间;
③这200名学生中的高中生参加公益劳动时间的中位数可能在20h~30h之间;
④这200名学生中的初中生参加公益劳动时间的中位数一定在20h~30h之间.
所有合理推断的序号是( )
A.①②③④ B.①②④ C.①②③ D.①④
【解答】解:①解这200名学生参加公益劳动时间的平均数:①(24.5×97+25.5×103)÷200=25.015,一定在24.5~25.5之间,正确;
②由统计表类别栏计算可得,各时间段人数分别为 15,60,51,62,12,则中位数在20~30 之间,故②正确.
③由统计表计算可得,高中学段栏各时间段人数分别为 0﹣15,35,15,18,1,当0≤t<10时间段人数为 0 时,中位数在 10~20 之间;当 0≤t<10时间段人数为 15 时,中位数在 10~20 之间,故③错误.
④由统计表计算可得,初中学段栏0≤t<10 的人数在 0~15 之间,当人数为 0 时中位数在 20~30 之间;当人数为 15 时,中位数在 20~30 之间,故④正确.
故选:B.
二.填空题(共8小题,满分16分,每小题2分)
9.(2分)只有 符号 不同的两个数叫互为相反数.0的相反数是 0 ,1的相反数是 ﹣1 .
【解答】解:只有符号不同的两个数叫互为相反数.0的相反数是0,1的相反数是﹣1.
故答案为:符号;0;﹣1.
10.(2分)分解因式:x3﹣xy2= x(x+y)(x﹣y) .
【解答】解:原式=x(x2﹣y2)
=x(x+y)(x﹣y).
故答案为:x(x+y)(x﹣y).
11.(2分)在一个不透明的盒子中,装有除颜色外完全相同的乒乓球共24个,从中随机摸出一个乒乓球,若摸到黄色乒乓球的概率为,该盒子中装有黄色乒乓球的个数是 9 .
【解答】解:设盒子中黄色乒乓球的个数为x,
根据题意,得:=,
解得x=9,
∴该盒子中装有黄色乒乓球的个数是9,
故答案为:9.
12.(2分)如图,△ABC内接于⊙O,若∠AOB=110°,则∠C= 55 度.
【解答】解:∵∠C与∠AOB是同弧所对的圆周角与圆心角,∠AOB=110°,
∴∠ACB=∠AOB=55°.
故答案为:55.
13.(2分)某型号飞机的机翼形状如图所示,根据图中数据计算AB的长为 (﹣1.6) m.(结果保留根号)
【解答】解:如图,
在Rt△DEA中,∠ADE=45°,
∴AE=DE=5m,
DA==5(m);
在Rt△BCF中,∵cos∠BCF=,
∴CB==(m),
∴BF=BC=(m),
∵AB+AE=EF+BF,
∴AB=3.4+﹣5=﹣1.6(m).
答:AB的长为(﹣1.6)m.
故答案为:(﹣1.6).
14.(2分)将直线y=2x向下平移3个单位长度后,得到的直线经过点(m+2,﹣5),则m的值为 ﹣3 .
【解答】解:直线y=2x向下平移3个单位长度后的函数解析式是y=2x﹣3,
把x=m+2,y=﹣5代入y=2x﹣3,可得:2(m+2)﹣3=﹣5,
解得:m=﹣3,
故答案为:﹣3.
15.(2分)用一个a的值说明命题“若a2>1,则a>1”是假命题,这个值可以是a= ﹣2(答案不唯一) .
【解答】解:当a=﹣2时,a2=4>1,而﹣2<1,
∴命题“若a2>1,则a>1”是假命题,
故答案为:﹣2(答案不唯一).
16.(2分)上学期学校举办了“SD杯古诗词”竞赛.小宇、小尧、小非三位同学进入了最后冠军的角逐.决
赛共分六轮,规定:每轮分别决出第1,2,3名(不并列),对应名次的得分都分别为a,b,c(a>b>c且a,b,c均为正整数);选手最后得分为各轮得分之和,得分最高者为冠军.
下表是三位选手在每轮比赛中的部分得分情况,根据题中所给信息,
第一轮
第二轮
第三轮
第四轮
第五轮
第六轮
最后得分
小宇
a
a
26
小尧
a
b
c
11
小非
b
b
11
判断下列说法一定错误的是 ①②③ .(填序号)
①小宇可能有一轮比赛获第二名;
②小尧有三轮比赛获第三名;
③小非可能有一轮比赛获第一名;
④每轮比赛第一名得分a为5.
【解答】解:由题可知:(a+b+c)×6=26+11+11=48,其中a>b>c且a,b,c均为正整数.
∴a+b+c也是正整数,
∴a+b+c=8.
∵若每轮比赛第一名得分a为4,则最后得分最高为:4×6=24<26,
∴a>4,
∵又a>b>c,b+c最小取3,
∴4<a<6.
∴a=5,b=2,c=1,
∴每轮比赛第一名得分a为5,小宇5轮得第一,1轮得第三;小尧4轮得第三,1轮得第一,1轮得第二;小非5轮得第二,1轮得第三.
故答案为:①②③.
三.解答题(共12小题,满分68分)
17.(5分)计算:|﹣2|﹣(π﹣2019)0+()﹣2﹣2sin60°+.
【解答】解:原式=2﹣1+4﹣2×+2
=2﹣1+4﹣+2
=5+.
18.(5分)解下列不等式,并把解在数轴上表示出来.
(1)5x﹣5<2(2+x);
(2)>1;
(3);
(4)x(x+4)≤(x+1)2+9.
【解答】解:(1)去括号得,5x﹣5<4+2x,
移项得,5x﹣2x>4+5,
合并同类项,3x>9,
∴x>3.
在数轴上表示此不等式的解集如下:
(2)去分母,得4x﹣1﹣3x>3,
移项,得4x﹣3x>3+1,
合并同类项,得x>4,
∴x>4.
在数轴上表示此不等式的解集如下:
(3)去分母,得12≥4x﹣(2x﹣3),
去括号,得12≥4x﹣2x+3,
移项,得﹣4x+2x≥3﹣12,
合并同类项,得﹣2x≥﹣9,
∴x≤4.5.
在数轴上表示此不等式的解集如下:
(4)去括号,得x2+4x≤x2+2x+1+9,
移项,得x2﹣x2+4x﹣2x≤1+9,
合并同类项,得2x≤10,
∴x≤5.
在数轴上表示此不等式的解集如下:
19.(5分)(1)计算:
(2)计算:
(3)先化简,再求值:
已知=3,求的值.
【解答】解:(1)
=
=;
(2)
=•
=•
=x﹣1;
(3)
=÷
=•
=
∵=3,
∴a=3b,
故原式==﹣5.
20.(5分)如图,已知△ABC中,∠ACB=60°,BC<AB<AC.
(1)求作∠PBC,使得∠PBC=30°且点P在AC上;
(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若AB=4,∠A=45°,求AC的长度.
【解答】解:(1)如图,∠PBC即为所求.
(2)如图,由(1)得∠APB=∠BPC=90°,
∵∠A=45°,
∴∠ABP=45°,∠PBC=30°,
在Rt△ABP中,AP=BP=AB•sin45°=,
在Rt△BPC中,PC=BP•tan30°=,
∴.
21.(5分)已知关于x的一元二次方程x2+(m+2)x+2m=0.
(1)求证:方程总有两个实数根;
(2)若该方程有一个根大于3,求m的取值范围.
【解答】(1)证明:∵a=1,b=m+2,c=2m,
∴Δ=b2﹣4ac=(m+2)2﹣4×1×2m=m2+4m+4﹣8m=m2﹣4m+4=(m﹣2)2.
∵无论m取何值时,(m﹣2)2≥0,即△≥0,
∴原方程总有两个实数根.
(2)解:∵x2+(m+2)x+2m=0,即(x+2)(x+m)=0,
∴x1=﹣2,x2=﹣m.
∵该方程有一个根大于3,
∴﹣m>3,
∴m<﹣3.
22.(5分)如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、作CE∥BD,DE∥AC,CE和DE交于点E
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=10时,求CE和AE的长.
【解答】(1)证明:∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,即∠DOC=90°,
∴平行四边形ODEC是矩形;
(2)解:∵在Rt△AOD中,∠ADO=60°,
∴∠OAD=30°,
∵AD=10 OD=AD=5,
∴AO==5,
∵四边形ABCD是菱形,
∴AC=2A0=10,
∵四边形ODEC是矩形,∠ACE=90°,CE=OD=5,
在Rt△ACE中,由勾股定理得:AE===.
23.(6分)如图,一次函数y=kx+b的图象交反比例函数y=的图象于A(2,﹣4),B(a,﹣1)两点.
(1)求反比例函数与一次函数解析式.
(2)连接OA,OB,求△OAB的面积.
(3)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?
【解答】解:(1)把A(2,﹣4)的坐标代入y=得:m=﹣8,
∴反比例函数的解析式是y=﹣;
把B(a,﹣1)的坐标代入y=﹣得:﹣1=﹣,
解得:a=8,
∴B点坐标为(8,﹣1),
把A(2,﹣4)、B(8,﹣1)的坐标代入y=kx+b,得:,
解得:,
∴一次函数解析式为y=x﹣5;
(2)设直线AB交x轴于C.
∵y=x﹣5,
∴当y=0时,x=10,
∴OC=10,
∴△AOB的面积=△AOC的面积﹣三角形BOC的面积
=×10×4﹣×10×1
=15;
(3)由图象知,当0<x<2或x>8时,一次函数的值大于反比例函数的值.
24.(6分)如图,⊙O与△ABC的AC边相切于点C,与BC边交于点E,⊙O过AB上一点D,且DE∥AO,CE是⊙O的直径.
(1)求证:AB是⊙O的切线;
(2)若BD=4,EC=6,求AC的长.
【解答】(1)证明:连接OD,
∵OD=OE,
∴∠OED=∠ODE,
∵DE∥OA,
∴∠ODE=∠AOD,∠DEO=∠AOC,
∴∠AOD=∠AOC,
∵AC是切线,
∴∠ACB=90°,
在△AOD和△AOC中
,
∴△AOD≌△AOC(SAS),
∴∠ADO=∠ACB=90°,
∵OD是半径,
∴AB是⊙O的切线;
(2)解:∵AB是⊙O的切线,
∴∠BDO=90°,
∴BD2+OD2=OB2,
∴42+32=(3+BE)2,
∴BE=2,
∴BC=BE+EC=8,
∵AD,AC是⊙O的切线,
∴AD=AC,
设AD=AC=x,
在Rt△ABC中,AB2=AC2+BC2,
∴(4+x)2=x2+82,
解得:x=6,
∴AC=6.
25.(6分)为全力抗击疫情,响应政府“停课不停学”的号召,某市教育局发布关于疫情防控期间开展在线课程教学的通知:从2月10日开始,全市初高中毕业班按照教学计划,开展在线课程教学和答疑,据互联网后台数据显示,某中学九年级七科老师3月5日在线答疑问题各学科个数如下表:
学科
语文
数学
英语
物理
化学
道德与法治
历史
数量/个
27
28
28
26
23
21
22
(1)直接写出九年级七科老师3月5日在线答疑问题各学科个数的众数与中位数;
(2)计算九年级七科老师在线答疑问题各学科个数的平均数.
【解答】解:(1)九年级七科老师3月5日在线答疑问题各学科个数中,28出现次数最多,共出现2次,因此众数是28,
将这七科老师在线答疑问题各学科个数从小到大排列后,处在中间位置的一个数是26,因此中位数是26,
答:众数是28,中位数是26;
(2)平均数为:=25(个),
答:九年级七科老师在线答疑问题各学科个数的平均数为25个.
26.(6分)如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.
(1)求证:△FAC≌△BAE;
(2)图中可以通过旋转△BAE而得到△FAC,请你说出旋转中心、旋转方向和旋转角的度数.
【解答】证明:(1)∵四边形ABGF和四边形ACDE是正方形,
∴AF=AB,AC=AE,
∵∠BAF=∠CAE=90°,
∴∠BAF+∠BAC=∠CAE+∠BAC,
即∠FAC=∠BAE,
在△FAC和△BAE中,
,
∴△FAC≌△BAE(SAS);
(2)解:以点A为旋转中心,顺时针旋转90°得到△FAC.
27.(7分)已知二次函数y=ax2﹣2ax﹣2图象经过点P(﹣1,1).
(1)求a的值和图象的顶点坐标;
(2)若点Q(m,n)在该二次函数图象上,当﹣1≤m<4时,请根据图象直接写出n的取值范围.
【解答】解:(1)把P(﹣1,1)代入y=ax2﹣2ax﹣2中,
∴a=1,
∴y=x2﹣2x﹣2=(x﹣1)2﹣3
∴图象的顶点坐标为(1,﹣3);
(2)如图所示:
点Q(m,n)在该二次函数图象上,当﹣1≤m<4时,﹣3≤n<6.
28.(7分)如图,在等腰直角△ABC中,∠B=90°,AB=BC=4.动点P以每秒2个单位长度的速度沿射线AB运动,过点P作PF⊥AC于点F,以AF,AP为邻边作▱FAPG;▱FAPG与等腰直角△ABC的重叠部分面积为y(平方单位),y>0,点F与点C重合时运动停止,设点P的运动时间为x秒.
(1)直接写出点G落在BC边上时x的值.
(2)求y与x的函数关系式.
(3)直接写出点G与△ABC各顶点的连线平分△ABC面积时x的值.
【解答】解:(1)如图1,点G在BC上,
∵∠B=90°,AB=BC,
∴∠A=∠C=45°,
∵PF⊥AC,
∴∠AFP=90°,
∴∠A=∠APF=45°,
∴AF=PF;
∵四边形FAPG是平行四边形,
∴PG∥AC,AF=PG,
∴AF=PG=PF,∠BPG=∠A=45°,∠BGP=∠C=45°,
∵PA=2x,
∴AF=PG=PF=AP•sin45°=2x•=x,
∴PB=BG=PG•sin45°=x•=x,
∵PA+PB=AB=4,
∴2x+x=4,
解得,x=.
(2)∵∠B=90°,AB=BC=4,
∴AC===,
当点F与点C重合时,则x=,解得,x=4,
当点P与点B重合时,则2x=4,解得x=2.
当0<x≤时,如图2,y=S平行四边形FAPG=AF•PF=x•x,
即y=2x2;
当<x≤2时,如图3,PG交BC于点M,FG交BC于点N,作PQ⊥FG于点Q,
∵∠BMP=∠C=45°=∠BPG,
∴MB=PB=4﹣2x;
∵∠FPG=∠AFP=90°,PG=PF,FG=AP=2x,
∴FQ=GQ,
∴PQ=FG=×2x=x;
∵FG∥AB,
∴∠BPQ=∠PQF=90°,
∴∠B=∠BPQ=∠PQN=90°,
∴四边形BPQN是矩形,
∴BN=PQ=x,
∵∠G=∠A=45°,∠NMG=∠C=45°,
∴∠G=∠NMG,
∴GN=MN=x﹣(4﹣2x)=3x﹣4,
∴y=S平行四边形FAPG﹣S△NMG=2x2﹣(3x﹣4)2,
即y=﹣x2+12x﹣8;
当2<x≤4时,如图4,∵∠CFN=∠A=∠C=45°,
∴FN=CN=4﹣x,
∵∠CNF=∠ABC=90°,
y=S△ABC﹣S△NCF=×4×4﹣(4﹣x)2,
即y=﹣x2+4x.
综上所述,.
(3)如图5,点G在△ABC的中线CK上,则直线CG平分△ABC的面积,
∵PG∥AC,
∴△PKG∽△AKC,
∴,
∵AK==×4=2,
∴PK=2﹣2x,
∴,
解得,x=;
如图6,点G在△ABC的中线BL上,则直线BG平分△ABC的面积,
∵BL⊥AC,
∴∠FPG=∠PFL=∠FLG=90°,
∴四边形PFLG是矩形,
∴FL=PG=AF=x,
∵AL=AC=×4=2
∴x+x=,
解得,x=1,
综上所述,x的值为或1.
2022年北京市中考数学模拟试卷(word版含答案): 这是一份2022年北京市中考数学模拟试卷(word版含答案),共19页。试卷主要包含了估计26-4的值应在,因式分解等内容,欢迎下载使用。
2022年北京市顺义区中考数学模拟试卷(word版含答案): 这是一份2022年北京市顺义区中考数学模拟试卷(word版含答案),共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022年北京市朝阳区中考数学模拟试卷(word版含答案): 这是一份2022年北京市朝阳区中考数学模拟试卷(word版含答案),共10页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












