2021届河北省承德高三二模数学试卷及答案

2021届河北省承德高三二模数学试卷及答案

一、单选题

1．已知集合，，则（       ）

A． B． C． D．

2．设且，若复数是实数，则（       ）

A．9 B．6 C．3 D．2

3．若，，则（       ）

A． B． C． D．

4．双曲线的一个焦点到渐近线的距离为（       ）

A． B． C． D．

5．设平面向量，若，，则（       ）

A．2 B．3 C．9 D．6

6．人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律，可以为有效控制人口增长提供依据.我国在2020年进行了第七次人口普查登记，到2021年4月以后才能公布结果.人口增长可以用英国经济学家马尔萨斯(T.R.Malthus，1766—1834)提出的模型：，其中t表示经过的时间，表示时的人口数，r表示人口的年平均增长率.以国家统计局发布的2000年第五次人口普查登记(已上报户口)的全国总人口12.43亿人(不包括香港､澳门和台湾地区)和2010年第六次人口普查登记(已上报户口)的全国总人口13.33亿人(不包括香港､澳门和台湾地区)为依据，用马尔萨斯人口增长模型估计我国2020年末(不包括香港､澳门和台湾地区)的全国总人口数约为（       ）(，)

A．14.30亿 B．15.20亿 C．14.62亿 D．15.72亿

7．在三棱柱中，侧棱底面ABC.所有棱长都为1，E，F分别为棱BC和的中点，若经过点A，E，F的平面将三棱柱分割成两部分，则这两部分体积的比值为（       ）

A． B． C． D．

8．对于任意，总存在三个不同的实数，使得成立，则实数a的取值范围是（       ）

A． B． C． D．

二、多选题

9．已知直线与圆，则下列说法中正确的是（       ）

A．直线l与圆M一定相交

B．若，则直线l与圆M相切

C．当时，直线l与圆M的相交弦最长

D．圆心M到直线l的距离的最大值为

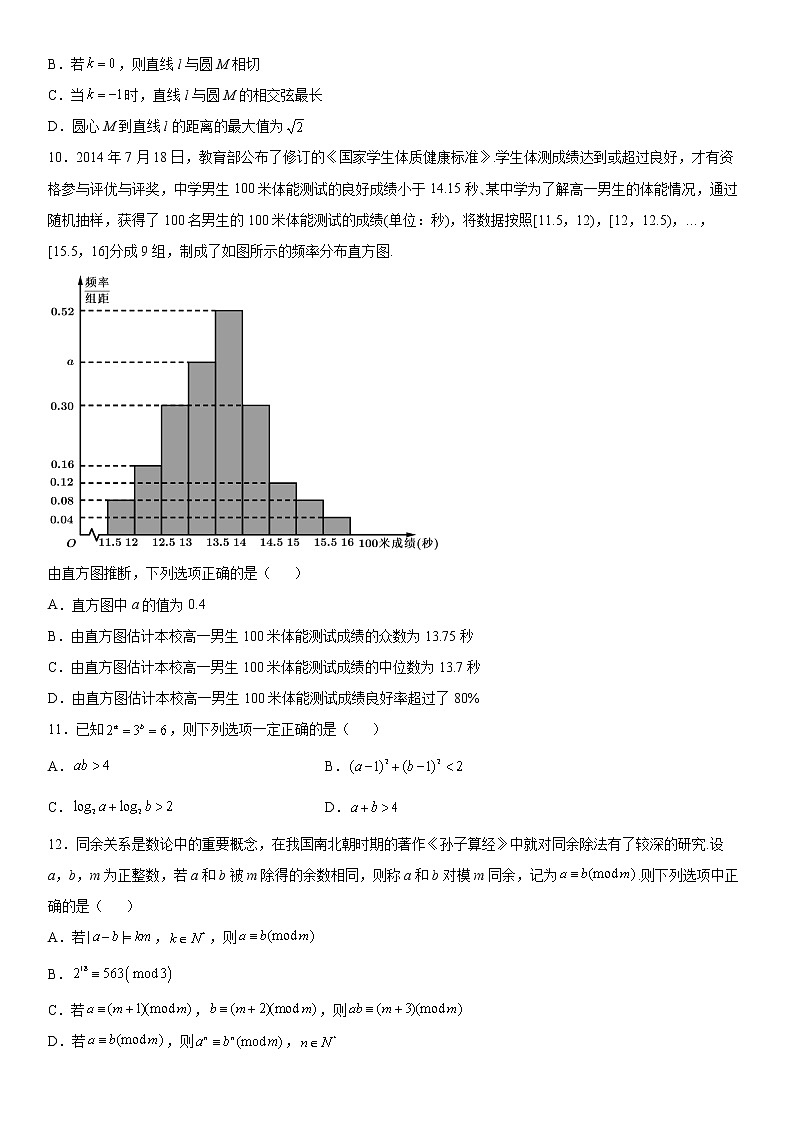
10．2014年7月18日，教育部公布了修订的《国家学生体质健康标准》.学生体测成绩达到或超过良好，才有资格参与评优与评奖，中学男生100米体能测试的良好成绩小于14.15秒､某中学为了解高一男生的体能情况，通过随机抽样，获得了100名男生的100米体能测试的成绩(单位：秒)，将数据按照[11.5，12)，[12，12.5)，…，[15.5，16]分成9组，制成了如图所示的频率分布直方图.

由直方图推断，下列选项正确的是（       ）

A．直方图中a的值为0.4

B．由直方图估计本校高一男生100米体能测试成绩的众数为13.75秒

C．由直方图估计本校高一男生100米体能测试成绩的中位数为13.7秒

D．由直方图估计本校高一男生100米体能测试成绩良好率超过了80%

11．已知，则下列选项一定正确的是（       ）

A． B．

C． D．

12．同余关系是数论中的重要概念，在我国南北朝时期的著作《孙子算经》中就对同余除法有了较深的研究.设a，b，m为正整数，若a和b被m除得的余数相同，则称a和b对模m同余，记为.则下列选项中正确的是（       ）

A．若，，则

B．

C．若，，则

D．若，则，

三、填空题

13．已知随机变量，若，则___________.

14．已如点，F为抛物线的焦点，过点F且斜率为k的直线l与抛物线C交于A，B两点，若，则k2的取值范围是___________.

15．某中学开展劳动实习，学习加工制作模具，有一个模具的毛坯直观图如图所示，是由一个圆柱体与两个半球对接而成的组合体，其中圆柱体的底面半径为1，高为2，半球的半径为1.现要在该毛坯的内部挖出一个中空的圆柱形空间，该中空的周柱形空间的上下底面与毛坯的圆柱体底面平行，挖出中空的圆柱形空间后模具制作完成，则该模其体积的最小值为___________.

四、双空题

16．当时，函数取得最大值为___________，且___________.

五、解答题

17．已知是数列的前n项和，且，.

（1）证明数列是等比数列，并求数列的通项.

（2）是否存在整数k，使得？若存在，求出k的最小值，若不存在，请说明理由.

18．已知在中，内角A，B，C的对边分别为a，b，c，.

（1）求B；

（2）若，，求的面积.

19．某中学的学习兴趣小组随机调查了该校110名学生的到校形式，整理后得到如下的列联表：

（1）根据列联表的数据判断，能否在犯错误的概率不超过0.01的前提下认为到校形式与性别有关系？

（2）若以上述样本的频率作为概率，在该校中随机抽取6人，用X表示6人中“独自到校”的人数，求X的数学期望和方差.

附表：

附：

20．如图，在四棱锥中，底面ABCD是菱形，，.

（1）证明：；

（2）若异面直线PB与CD所成角的余弦值为，求二面角的余弦值.

21．已知函数.

（1）当时，求曲线在点处的切线与两坐标轴围成的三角形的面积；

（2）若恒成立，求实数a的取值范围.

22．已知，，动点P满足：直线PM与直线PN的斜率之积为常数，设动点P的轨迹为曲线.抛物线与在第一象限的交点为A，过点A作直线l交曲线于点B.交抛物线于点E(点B，E不同于点A).

（1）求曲线的方程.

（2）是否存在不过原点的直线l，使点E为线段AB的中点？若存在，求出p的最大值；若不存在，请说明理由.

参考答案：

1．B

【解析】

【分析】

根据绝对值不等式的解法，结合集合交集的定义进行求解即可.

【详解】

因为，所以，，

故选：B.

2．C

【解析】

【分析】

对给定式子进行运算，利用复数为0的充要条件求解即得.

【详解】

因为，

所以，又，所以.

故选：C

3．A

【解析】

【分析】

对等式进行平方运算，用同角三角函数关系式中平方和关系进行代换，最后利用同角三角函数关系式中的商关系进行求解即可.

【详解】

，所以，解得或，又，所以.

故选：A

4．C

【解析】

【分析】

根据点到直线距离公式进行求解即可.

【详解】

设双曲线的一条渐近线方程为，

右焦点坐标为，又，

则焦点到渐近线的距离为，

故选：C.

5．D

【解析】

【分析】

根据平面向量夹角公式，结合平面向量模的坐标表示公式进行求解即可.

【详解】

.

故选：D

6．A

【解析】

【分析】

利用给定公式计算出，然后以2010年底的人口数为基数求t=10时的值即为所求.

【详解】

由马尔萨斯模型，得，即，

所以我国2020年末的全国总人口数(亿).

故选：A.

7．D

【解析】

【分析】

如图，平面AEF与交于点G，根据题意可以判断为三棱台，根据棱柱的体积公式和棱台体积公式进行求解即可.

【详解】

解析：如图，平面AEF与交于点G，且，故为三棱台，

因为，所以，，

所以棱台的体积：

，

三棱柱的体积，所以，

故选：D.

【点睛】

关键点睛：根据已知判断为三棱台是解题的关键.

8．B

【解析】

【分析】

对等式进行变形，根据等式特征构造两个分别关于函数，根据所给区间，利用导数求出每个函数的单调性及取值范围，

【详解】

由，得，设，.

因为，故当时，，

所以函数在上单调递增，所以.

因为，故当时，，当时，，

当时，，所以函数在上单调递减，在上单调递增，

在上单调递减，且，

函数在上的图象如下图所示：

要总存在三个不同的实数，使得，

只要且，所以.

故选：B.

【点睛】

方法点睛：关于方程有根的问题一般采用构造函数，利用导数判断出在指定区间的单调性和值域，结合数形结合思想进行求解.

9．BCD

【解析】

【分析】

A.由直线l过原点，再判断原点与圆的位置关系即可； B.利用圆心到直线的距离和半径的关系判断；C.由直线l的方程为，判断是否过圆M的圆心即可；D.建立圆心到直线距高公式模型求解判断

【详解】

，即，是以为圆心，以1为半径的圆，

A.因为直线，直线l过原点，，原点在圆外，所以直线l与圆M不一定相交，故错误；

B.若，则直线，直线l与圆M相切，故正确；

C.当时，直线l的方程为，过圆M的圆心，故正确；

D.由点到直线距高公式，知(当时，等号成立).故正确，

故选：BCD.

10．AB

【解析】

【分析】

A：根据各组频率之和为1，进行求解判断即可；

B：根据直方图的众数是频率最高组的中点进行判断即可；

C：根据直方图的中位数是频率相等的分点进行判断即可：

D：根据直方图求出成绩小于14.15秒的人数所占百分比进行判断即可.

【详解】

A：由概率统计相关知识，可知各组频率之和为1.

频率=(频率/组距)×组距，

，解得，故A正确；

B：直方图的众数是频率最高组的中点，即，故B正确；

C：直方图的中位数是频率相等的分点，设为x，

则，

解得，故C错误；

D：由图可知.成绩小于14.15秒的人数所占百分比为：

，

故D错误.

故选：AB

11．ACD

【解析】

【分析】

根据指数式与对数式互化公式，结合基本不等式进行判断即可.

【详解】

由，得，，，

所以，，又，所以，故A正确；

因为，

所以，故B错误；

因为，又，所以，故C正确；

因为，又，所以，D正确，

故选：ACD.

【点睛】

关键点睛：根据指数式与对数式互化公式、对数的运算性质得到是解题的关键.

12．AD

【解析】

【分析】

A：根据绝对值的性质，结合已知的定义进行判断即可；

B：运用二项式定理进行判断即可；

C：根据已知通过数学运算计算判断即可；

D：根据已知结合二项式定理进行判断即可.

【详解】

A：若，则或，故，故A正确；

B：因为，所以218被3除得的余数为1，563除得的余数为2，故B错误；

C：由得，由，得，

，ab被m除得的余数为2，而被m除得余数为3，故C错误；

D：若，则，，

，

，

所以，故D正确，

故选：AD.

【点睛】

关键点睛：读懂同余关系的定义，并转化为数学式子是解题的关键.

13．0.2

【解析】

【分析】

利用正态分布的对称性列式计算求解而得.

【详解】

由，得，，

所以.

故答案为：0.2

14．(0，4]

【解析】

【分析】

设，，直线l的方程为，联立直线和抛物线方程得到韦达定理，代入化简即得解.

【详解】

由题意，知，设，，直线l的方程为，

由得，

所以，.

由，得

又，，所以，所以.

又，所以，故.

故答案为：(0，4]

【点睛】

方法点睛：圆锥曲线中最值范围问题常用的方法有：（1）函数法；（2）导数法；（3）数形结合法；（4）基本不等式法. 要根据已知条件灵活选择方法求解.

15．

【解析】

【分析】

设中空圆柱的底面半径为，圆柱的高为，把圆柱的体积用含有的代数式表示，利用导数求其最大值，即可求得模具体积的最小值．

【详解】

设中空圆柱的底面半径为，圆柱的高为，

则，，

中空圆柱的体积．

，可得当时，，当，时，，

则当时，取得最大值为，

又毛坯的体积为，

该模具体积的最小值为．

故答案为：．

【点睛】

关键点点睛：本题解题关键是利用单变量来表示体积，然后利用导数法求出最值.

16．          2

【解析】

【分析】

根据辅助角公式，正弦型函数的性质，结合同角的三角函数关系式、诱导公式进行求解即可.

【详解】

解析：，，

当，即时，的函数值最大，

故，

.

故答案为：；2

17．（1）证明见解析，；（2）存在，k最小为10.

【解析】

【分析】

（1）根据问题对递推公式进行变形，结合等比数列的定义进行求解即可；

（2）根据等比数列的前n项和公式，结合做差比较法判断出数列的单调性进行求解即可.

【详解】

（1）由，得，

所以.，故数列是以4为首项，2为公比的等比数列，

所以，

所以.

（2）由（1），得，

又当时，，，

，

，

故当k最小为10时，.

【点睛】

关键点睛：利用做差比较法判断数列的单调性是解题的关键.

18．（1）；（2）.

【解析】

【分析】

(1)利用正弦定理边化角，再用三角函数诱导公式及和角化简求解而得；

(2)利用余弦定理求出边c，再用三角形面积定理求解即得.

【详解】

（1）在中，由正弦定理，得，

又，所以，

即，

即，又，所以；

（2）由余弦定理得，得，

解得，

所以.

【点睛】

解三角形的基本策略：一是利用正弦定理实现“边化角”，二是利用余弦定理实现“角化边”.

19．（1）错误的概率不超过0.01的前提下认为到校形式与性别有关系；（2），.

【解析】

【分析】

（1）根据题中所给的公式以及附表进行计算求解判断即可；

（2）根据二项分布的定义、数学期望和方差公式进行求解即可.

【详解】

解：（1）假设性别与到校形式无关，根据列联表中的数据，得到

，

因此，错误的概率不超过0.01的前提下认为到校形式与性别有关系.

（2）X的可能取值为0，1，2，3，4，5，6.

若以样本的频率视为概率，则在该校中随机抽取1人为“独自到校”的概率为，

在该校中随机抽取6人，可视为6次独立重复试验，

所以，

故，.

20．（1）证明见解析；（2）.

【解析】

【分析】

（1）设AD的中点为O，利用等边三角形的性质、菱形的性质，结合线面垂直的判定定理进行证明即可；

（2）根据异面直线所成角的定义，结合（1）建立空间直角坐标系，利用空间向量夹角公式进行求解即可.

【详解】

（1）证明：如图，设AD的中点为O，连接OP，OB，BD.

由，，，可知，为等边三角形，

又点O为AD的中点，所以，.

又，故平面POB.

又平面POB，

所以.

（2）解：不妨设，则.

由，得，又，

，

解得，

在中，，所以.

由（1）可知，，故PO，OB，AD两两垂直.

以O为坐标原点，分別以OA，OB，OP所在直线为x轴､y轴､z轴的正方向，建立如图所示的空间直角坐标系.

则，，，.

设为平面APB的法向量，

则，即可取.

设为平面PBC的法向量，

则，即可取.

.

由题意，可知二面角的平面角为钝角，

二面角的余弦值为.

21．（1）；（2）.

【解析】

【分析】

（1）利用导数的几何意义求出切线方程，最后根据切线与横轴、纵轴的交点坐标进行求解即可；

（2）构造函数，判断其奇偶性，问题转化为：当时，恒成立，经过三次求导，根据导数的性质进行求解即可.

【详解】

解：（1）因为，所以，故.

又，所以切点坐标为，

故函数在点处的切线方程为，即，

所以切线与坐标轴交点坐标分别为，，

故所求三角形面积为.

（2）由，得恒成立，

令，则，所以为偶函数.

故只要求当时，恒成立即可.

，

设，故，

设，则，

显然为的増函数，故，

即在上单调递增，.

当时，，则有在上单调递增，故，

则在上单调递增，故，符合题意；

当时，，又，故存在，使得，

故在上单调递减，在上单调递增.

当时，，故在上单调递减，

故，与矛盾.

综上，实数a的取值范围为.

【点睛】

关键点睛：解题的关键第一是构造函数，利用函数的奇偶性进行转化问题求解；第二是三次求导，利用导数的性质进行求解.

22．（1）；（2）存在，p的最大值为.

【解析】

【分析】

（1）利用斜率公式进行求解即可；

（2）根据直线l与椭圆的方程联立、直线l与抛物线方程联立、抛物线方程与椭圆方程联立，结合一元二次方程根与系数、中点坐标公式、基本不等式进行求解判断即可.

【详解】

解：（1）设动点，则，.

，，

即，

即，

曲线C1的方程为.

（2）设，，，显然直线l存在斜率，

设，

，

，.

又，

，

，因此有，

，，

，

设，

当且仅当时取等号，即当时取等号，

则，当时，，

当，即时，取得最大值，最大值为，即.

此时，直线不过点M，N.

故存在不过原点的直线，使点E为线段AB的中点，且p的最大值为.

【点睛】

关键点睛：通过解方程组求出相应点的坐标，运用基本不等式进行求解是解题的关键.