2020-2021学年广东省深圳市龙岗区龙岭中学七年级（下）第一次月考数学试卷

2020-2021学年广东省深圳市龙岗区龙岭中学七年级（下）第一次月考数学试卷

1. 一种感冒病毒的直径约为，将这个数用科学记数法可表示为

A.  B.  C.  D.

2. 下列计算正确的是

A.  B.  C.  D.

3. 计算的结果是

A.  B.  C.  D.

4. 下列各式中，不能够用平方差公式计算的是

A.  B.
C.    D.

5. 若，则整式M为

A.  B. 2xy C.  D. 4xy

6. 如果一个单项式与的积为，则这个单项式为

A.  B.  C.  D.

7. 若，，则的值为

A. 5 B. 4 C. 3 D. 1

8. 比较、、的大小

A.  B.  C.  D.

9. 已知，，则的值是

A. 24 B. 36 C. 72 D. 6

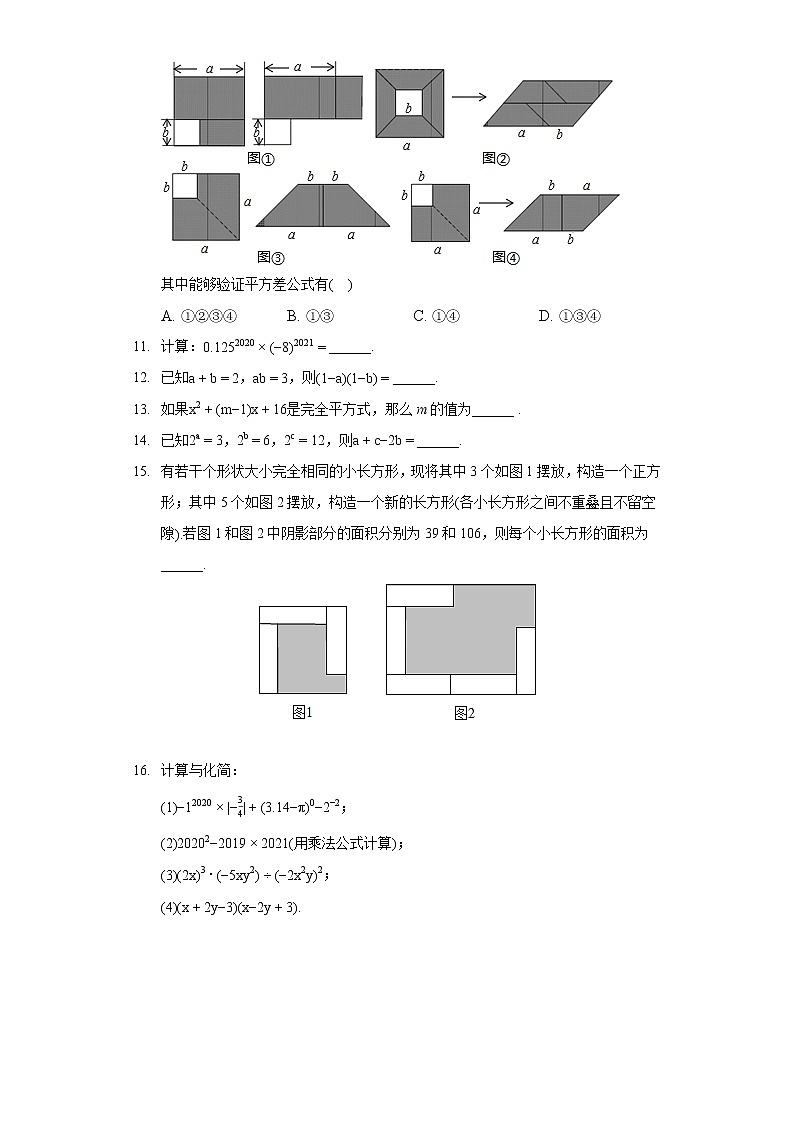
10. 如图，阴影部分是边长是a的大正方形剪去一个边长是b的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，给出下列4幅图割拼方法：
    
    其中能够验证平方差公式有

A. ①②③④ B. ①③ C. ①④ D. ①③④

11. 计算：______.
12. 已知，，则______.
13. 如果是完全平方式，那么m的值为______ .
14. 已知，，，则______.
15. 有若干个形状大小完全相同的小长方形，现将其中3个如图1摆放，构造一个正方形；其中5个如图2摆放，构造一个新的长方形各小长方形之间不重叠且不留空隙若图1和图2中阴影部分的面积分别为39和106，则每个小长方形的面积为______.

16. 计算与化简：
    ；
    用乘法公式计算；
    ；
    
    
    
    
    
    
    
     
17. 先化简，再求值：，其中，
    
    
    
    
    
    
     
18. 已知多项式与的乘积中不含项和x项，试求m和n的值，并求这两个多项式的乘积．
    
    
    
    
    
    
     
19. 如图，有一块长米，宽米的长方形广场，园林部门要对阴影区城进行绿化，空白区城进行广场硬化，阴影部分是边长为米的正方形．
    计算广场上需要硬化部分的面积；
    若，，求硬化部分的面积．
    
    
    
    
    
    
     
20. 用四个长为m，宽为n的相同长方形按如图方式拼成一个正方形．
    请用两种不同的方法表示图中阴影部分的面积．
    方法①：______；
    方法②：______.
    由 可得出，，4mn这三个代数式之间的一个等量关系为：______.
    利用中得到的公式解决问题：已知，，试求的值．
    
    
    
    
    
    
     
21. 如图1，边长为a的大正方形有一个边长为b的小正方形，把图1中的阴影部分拼成一个长方形如图2所示
    如图1，可以求出阴影部分的面积是______写成平方差的形式
    如图2，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是______，长是______，面积是______写成多项式乘法形式
    比较左、右两图的阴影部分面积，可以得到公式______.
    请应用这个公式完成下列各题：
    ①已知，，则______.
    ②计算：
    ③计算：
     

22. 如果，那么我们规定例如：因为，所以
    理解]根据上述规定，填空：______，______；
    说理]记，，试说明：；
    应用]若，求t的值．
    
    
    
    
    
    
    
    

答案和解析

1.【答案】B
 

【解析】

【分析】
本题考查用科学记数法表示较小的数，一般形式为，其中，n由原数左边起第一个不为零的数字前面的0的个数所决定.
绝对值小于1的正数用科学记数法表示为的形式，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【解答】
解：
故选  

2.【答案】D
 

【解析】解：，故本选项不合题意；
B.，故本选项不合题意；
C.，故本选项不合题意；
D.，故本选项符合题意．
故选：
分别根据幂的运算法则，合并同类项法则，积的乘方运算法则以及同底数幂的乘法法则逐一判断即可．
本题主要考查了合并同类项，同底数幂的乘法以及幂的乘方与积的乘方，熟记幂的运算法则是解答本题的关键．
 

3.【答案】B
 

【解析】

【分析】
此题考查多项式的乘法，关键是根据多项式乘法的法则解答．
根据多项式的乘法解答即可．
【解答】
解：，
故选：  

4.【答案】B
 

【解析】解：B、两项都是相反项的项，不能运用平方差公式；
A、C、D中均存在相同和相反的项，
故选：
运用平方差公式时，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方．
本题考查了平方差公式的应用，熟记公式是解题的关键．
 

5.【答案】D
 

【解析】解：因为，，
所以，
故选：
根据完全平方公式，即可解答．
本题考查了完全平方公式，解决本题的关键是熟记完全平方公式．
 

6.【答案】B
 

【解析】解：设这个单项式为A，
由题意得，，
，
故选：
根据单项式除以单项式的运算法则计算，得到答案．
本题考查的是单项式除以单项式，掌握单项式除以单项式的运算法则是解题的关键．
 

7.【答案】B
 

【解析】解：
故选：
依据平方根公式进行计算即可．
本题主要考查的是平方根公式，熟练掌握平方差公式是解题的关键．
 

8.【答案】C
 

【解析】解：，
，
，
，

故选：
根据幂的乘方，底数不变指数相乘都转换成指数是11的幂，再根据底数的大小进行判断即可．
本题考查了幂的乘方的性质，解题的关键在于都转化成以11为指数的幂的形式．
 

9.【答案】C
 

【解析】

【分析】
此题主要考查了同底数幂的乘法运算以及幂的乘方运算，正确将原式变形是解题关键．
直接利用同底数幂的乘法运算法则结合幂的乘方运算法则计算得出答案．
【解答】
解：，，



故选：  

10.【答案】A
 

【解析】解：图①，左边图形的阴影部分的面积，右边图形阴影部分的面积，
，故①可以验证平方差公式；
图②，阴影部分面积相等，左边的阴影部分的面积，右边图形阴影部分的面积，
，故②可以验证平方差公式；
图③，阴影部分面积相等，左边的阴影部分的面积，右边图形阴影部分的面积，
，故③可以验证平方差公式；
图④，阴影部分面积相等，左边的阴影部分的面积，右边图形阴影部分的面积，
，故④可以验证平方差公式．
正确的有①②③④．
故选：
分别对各个图形中的阴影面积用不同方法表示出来，即可得到等式，则可对各个选项是否可以验证平方差公式作出判断．
本题考查了平方差公式的几何背景，数形结合并熟练掌握相关几何图形的面积计算方法是解题的关键．
 

11.【答案】
 

【解析】解：





根据积的乘方运算法则计算即可，积的乘方，等于每个因式乘方的积．
本题主要考查了幂的乘方与积的乘方，熟记幂的运算法则是解答本题的关键．
 

12.【答案】2
 

【解析】解：

，
当，时，
原式

故答案为：
先把多项式乘以多项式展开，再整体代入求值即可．
本题主要考查了多项式乘以多项式的法则，考核学生的计算能力，整体代入是解题的关键．
 

13.【答案】9或
 

【解析】

【分析】
本题主要考查对完全平方公式的理解和掌握，能根据已知得出是解此题的关键．根据完全平方公式得出，代入求出即可．
【解答】
解：是完全平方式，
，
，
或，
故答案为9或  

14.【答案】1
 

【解析】解：，
即




故答案为：
先计算，再逆运用同底数幂的乘除法法则，代入求值即可．
本题考查了同底数幂的乘除法法则及幂的乘方法则，熟练掌握同底数幂的乘除法法则及逆运用，是解决本题的关键．
 

15.【答案】14
 

【解析】解：设小长方形的宽为a，长为b，根据题意可得：
，
故，
，
故，
则，
即，
则，
解得：，
故每个小长方形的面积为：
故答案为：
直接利用整式的混合运算法则结合已知阴影部分面积进而得出答案．
此题主要考查了整式的混合运算，正确掌握整式的混合运算法则是解题关键．
 

16.【答案】解：原式

；
原式

；
原式
；
原式



 

【解析】化简有理数的乘方，绝对值，零指数幂，负整数指数幂，然后再计算；
利用平方差公式进行简便计算；
先利用幂的乘方和积的乘方运算法则计算乘方，然后再算乘除；
将原式进行变形，然后利用平方差公式和完全平方公式进行计算．
本题考查整式的混合运算，掌握幂的乘方，积的乘方运算法则，完全平方公式和平方差公式是解题关键．
 

17.【答案】解：原式

，
当、时，
原式


 

【解析】先计算括号内的乘方和乘法，再合并括号内的同类项，最后计算除法即可得．
本题主要考查整式的化简求值能力，熟练掌握整式的混合运算顺序及运算法则是解题的关键．
 

18.【答案】解：由题意可知：，
不含项和x项，
，，
，
这两个多项式的乘积
 

【解析】根据多项式乘多项式的运算法则即可求出答案．
本题考查多项式乘多项式，解题的关键是熟练运用多项式乘以多项式，本题属于基础题型．
 

19.【答案】解：
根据题意，广场上需要硬化部分的面积是





答：广场上需要硬化部分的面积是
把，代入

答：广场上需要硬化部分的面积是
 

【解析】由题意可知空白部分的面积=长方形的面积-阴影部分的面积．长方形的面积是长宽，即；阴影部分是正方形，其面积是，所以空白部分的面积是；
将a，b的数值代入题中的代数式求值即可．
本题考查多项式乘多项式在几何图形中的应用．图中空白部分的面积不方便直接求出，可通过间接求面积法获得，这种方法在很多几何图形求面积的题目中应用广泛，需重点把握．
 

20.【答案】解：①；②；
；
由得：，



 

【解析】

【分析】
直接利用正方形的面积公式得到图中阴影部分的面积为；也可以用大正方形的面积减去4个长方形的面积得到图中阴影部分的面积为；
根据图中阴影部分的面积是定值得到等量关系式；
利用中的公式得到，再代入计算可得．
本题考查了列代数式与完全平分公式的几何背景，解决问题的关键是读懂题意，找到所求的量的等量关系．本题更需注意要根据所找到的规律做题．
【解答】
解：方法①：；
方法②：
故答案为①，②
因为图中阴影部分的面积不变，所以：
故答案为；
见答案．  

21.【答案】  或
 

【解析】解：大正方形面积，小正方形面积，
阴影部分面积=大正方形面积-小正方形面积，
故答案为：；
由图可知，长方形的宽，长方形的长，
长方形的面积，
故答案为，；；；
或；
①，，
，
故答案为：3；
②



；
③




由面积公式可得到答案；
根据图形可知长方形的长是，宽是，由长方形面积公式可得到答案；
根据图1和图2阴影部分面积相等可得到答案；
①根据平方差公式，，已知代入即可求出答案；
②可先把化为，再利用平方差公式计算即可得出答案；
③先利用平方差公式变形，再约分即可得到答案．
本题主要考查了平方差公式的几何背景及其应用与拓展，计算具有一定的难度，属于中档题．
 

22.【答案】
 

【解析】解：，，
，，
故答案为：3；；

证明：，，，
，，，
，
，
；

设，，，
，，，
，
，
，
，
即，

根据规定的两数之间的运算法则解答；
根据积的乘方法则，结合定义计算；
根据定义解答即可．
本题考查的是幂的乘方和积的乘方以及有理数的混合运算，掌握幂的乘方和积的乘方法则是解题的关键．