合肥市2022年高三第一次教学质量检测 文科数学试题

这是一份合肥市2022年高三第一次教学质量检测 文科数学试题，共13页。试卷主要包含了答第Ⅱ卷时，必须使用0，若为角终边上的一点，则值等于，命题等内容，欢迎下载使用。
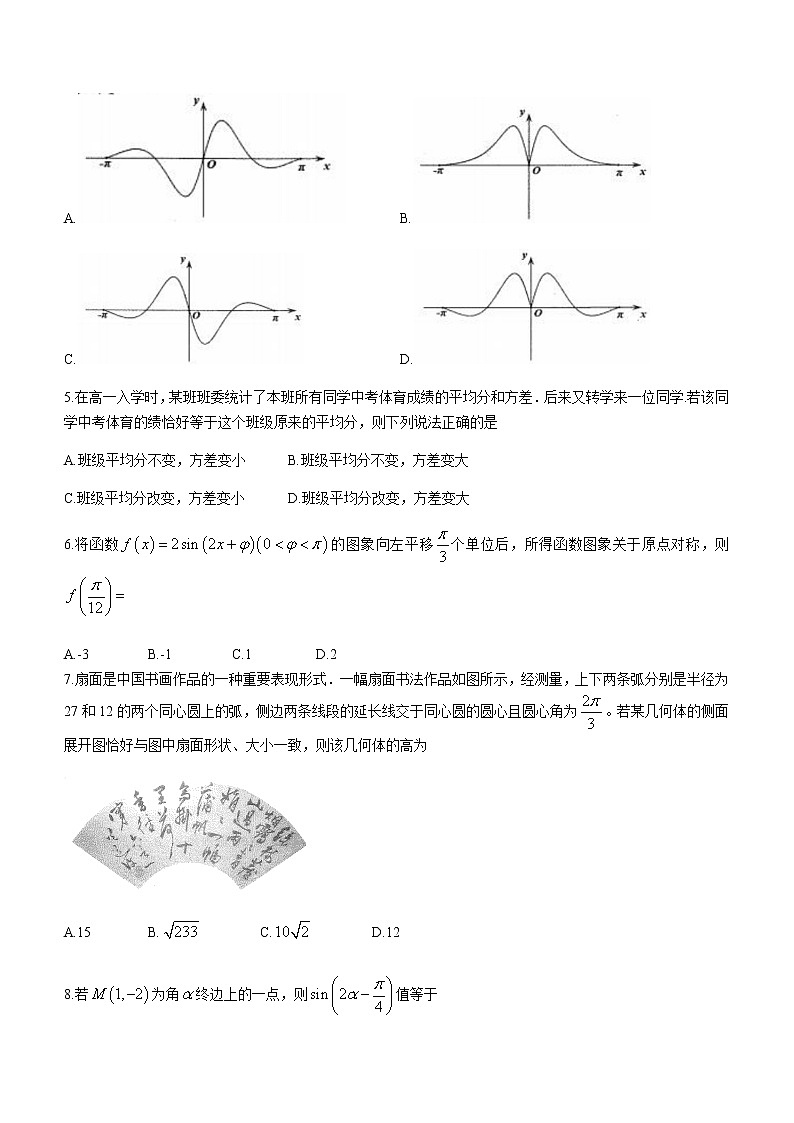
合肥市2022年高三第一次教学质量检测数学试题（文科）（考试时间：120分钟满分：150分）注意事项：1.答题前，务必在答题卡和答题卷规定的地方填写自己的姓名、准考证号和座位号后两位.2.答第I卷时，每小题选出答案后，用2B铅笔将答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.3.答第Ⅱ卷时，必须使用0.5毫米的黑色墨水签字笔在答题卷上书写，要求字体工整、笔迹清晰.作图题可先用铅笔在答题卷规定的位置绘出，确认后再用0.5毫米的黑色墨水签字笔描清楚.必须在题号所指示的答题区域作答，超出答题区域书写的答案无效，在试题卷、草稿纸上答题无效.4.考试结束，务必将答题卡和答题卷一并上交.第I卷（满分60分）一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1.集合，，则A.   B.   C.   D.2.若（i为虚数单位），则实数a的值为A.-3   B.-1   C.1   D.33.若向量，为单位向量，，则向量与向量的夹角为A.30°   B.60°   C.120°   D.150°4.函数在的图象大致为A.  B.C.    D.5.在高一入学时，某班班委统计了本班所有同学中考体育成绩的平均分和方差．后来又转学来一位同学.若该同学中考体育的绩恰好等于这个班级原来的平均分，则下列说法正确的是A.班级平均分不变，方差变小  B.班级平均分不变，方差变大C.班级平均分改变，方差变小  D.班级平均分改变，方差变大6.将函数的图象向左平移个单位后，所得函数图象关于原点对称，则A.-3   B.-1   C.1   D.27.扇面是中国书画作品的一种重要表现形式．一幅扇面书法作品如图所示，经测量，上下两条弧分别是半径为27和12的两个同心圆上的弧，侧边两条线段的延长线交于同心圆的圆心且圆心角为。若某几何体的侧面展开图恰好与图中扇面形状、大小一致，则该几何体的高为A.15   B.   C.   D.128.若为角终边上的一点，则值等于A.   B.   C.   D.9.若是定义在上的偶函数，对，当时，都有，则，，的大小关系是A.   B.   C.   D.10.命题：，（为自然对数的底数）；命题：，，则下列命题中，真命题是A.   B.   C.   D.11.椭圆的左焦点关于直线：的对称点是，连接FM并延长交椭圆C于点P.若，则椭圆C的离心率是A.   B.   C.   D.12.在四棱锥中，，，，，M是AC的中点若平面平面BCDE，则下列三个结论：①;②;③中，正确的是A.①②   B.①③   C.②③   D.①②③第Ⅱ卷（非选择题共90分）本卷包括必考题和选考题两部分．第13题—第21题为必考题，每个试题考生都必须作答．第22题、第23题为选考题，考生根据要求作答．二、填空题：本大题共4小题，每小题5分，满分20分．第16题第一空2分，第二空3分．把答案填在答题卡上的相应位置.13.双曲线的一个顶点为，焦距为6，其标准方程为___________.14.若x，y满足约束条件则的最小值为___________.15.曲线（为自然对数的底数）在处的切线与圆相交于点，，则___________.16.锐角的内角，，的对边分别为，，.若，则__________，的取值范围是__________.三、解答题：本大题共6小题，满分70分．解答应写出文字说明、证明过程或演算步骤．17.（本小题满分12分）已知数列的前项和为，2，，成等差数列．（1）求数列的通项公式；（2）设，求数列的前项和.18.（本小题满分12分）第24届冬奥会将于2022年2月4日在北京国家体育场开幕，“冬奥热”在国民中迅速升温。为了解冬奥会知识在某校高中生中的普及程度，该校按性别分层抽样，随机从高中生中抽取了50人参加测试，成绩统计图：（1）估计该校高中生男生和女生哪个群体掌握冬奥会知识的平均水平更高？（2）该校计划从得分为100分的高中生中随机抽取两名学生参加市级比赛，抽取的两名学生性别不同的概率。19.（本小题满分12分）如图，在三棱柱中，为棱的中点，平面.（1）试确定点的位置，并证明平面；（2）若是等边三角形，，，且平面平面，求四面体的体积．20.（本小题满分12分）在平面直角坐标系中，顶点在原点、以坐标轴为对称轴的抛物线经过点.（1）求抛物线的方程；（2）已知抛物线关于x轴对称，过焦点F的直线交C于A，B两点，线段AB的垂直平分线交直线AB于点P，交C的准线于点Q.若，求直线AB的方程。21.（本小题满分12分）已知函数.（1）讨论函数的单调性；（2）若函数有两个极值点，，且，证明：.请考生在第22、23题中任选一题作答．注意：只能做所选定的题目，如果多做，则按所做的第一个题目计分，作答时，请用2B铅笔在答题卡上，将所选题号对应的方框涂黑．22.（本小题满分10分）选修4-4：坐标系与参数方程在平面直角坐标系中，曲线的参数方程为（t为参数）.以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线的极坐标方程为.（1）求的普通方程和的直角坐标方程；（2）点P是曲线上的动点，过点P作直线与曲线有唯一公共点Q，求的最大值．23.（本小题满分10分）选修4-5：不等式选讲已知.（1）当时，求与所围成封闭图形的面积；（2）若对于任意的，都存在，使成立，求的取值范围．合肥市2022年高三第一次教学质量检测数学（文）试题参考答案及评分标准一、选择题：本大题共12小题，每小题5分，共60分.题号123456789101112答案BACDADCBABAD二、填空题：本大题共4小题，每小题5分，共20分.13.    14.-2    15.4    16.（1）；（2）三、解答题：17.（本小题满分12分）解：（1）∵2，，成等差数列，∴.当时，；当，且时，，，两式相减得，，即.∴数列是首项为2，公比为2的等比数列，.（2）∵，∴，①∴，②①-②：，∴.18.（本小题满分12分）解：（1）设男生和女生的平均得分分别为，，则，.∵，∴该校高中生男生群体掌握冬奥会知识的平均水平高于女生.（2）设男生中满分学生分别为，，，，女生满分学生分别为，，共6人，现从6人中随机抽取两人，共有如下15种可能：，，，，，，，，，，，，，，，其中性别不同的有如下8种可能：，；，；，；，.∴抽取的两名学生性别不同的概率为.19.（本小题满分12分）解：（1）延长，交的延长线于点N.∵，平面，∴平面.又∵，∴平面，点N即为所求.连接，交直线于点O，连接OM.∵，∴.又∵M为线段的中点，∴，即M为线段NB的中点.在三棱柱中，四边形为平行四边形，∴O为线段中点，∴OM为中位线，∴.又∵平面，平面，∴平面.（2）取线段的中点G，连接.由条件知，为等边三角形，∴，且.∵平面平面，平面平面，平面，∴平面，即是三棱锥的高.又∵，∴.由（1）知，，，∴，∴四面体的体积.20.（本小题满分12分）解：（1）当焦点在轴时，设抛物线：.将点坐标代入得，此时抛物线的方程为.当焦点在轴时，设抛物线：，将点坐标代入得，此时抛物线的方程为.综上，抛物线的方程为或.（2）当抛物线的焦点在轴时，其方程为.∵直线的斜率不存在时，，，不符合题意，∴直线的斜率存在，设直线的方程为，与抛物线的交点为，.由消去得，.∴，，∴，线段AB的中点P为，∴直线PQ的方程为.令，得，∴，∴.由得，，解得，∴直线的方程为或.21.（本小题满分12分）解：（1），.∵，，∴当时，，所以，当时，在上单调递增；当时，令，即，解得，.所以，当时，在，，上单调递增，在上单调递减.（2）由（1）知，若函数有两个极值点，则，，，.设，则.∵，∴.设，易知在单调递减，且，∴在恒成立，在区间单调递增，∴，∴.22.（本小题满分10分）解：（1）∵曲线的参数方程为（t为参数）由得，，∴曲线的普通方程为.∵曲线的极坐标方程为，，，∴曲线的直角坐标方程为，即.（2）设，，记，∴，∴当时，取最大值27，∵，∴的最大值为.23.（本小题满分10分）解：（1）由条件作出函数的图象和直线，记交点为，.易求，，.如图，所围图形为梯形ABCD，梯形的高为3，另一底长为3，∴封闭图形的面积为.（2）对，，，等价于，，，等价于.∵，，当且仅当时取等号，∴，解得或，∴的取值范围为.