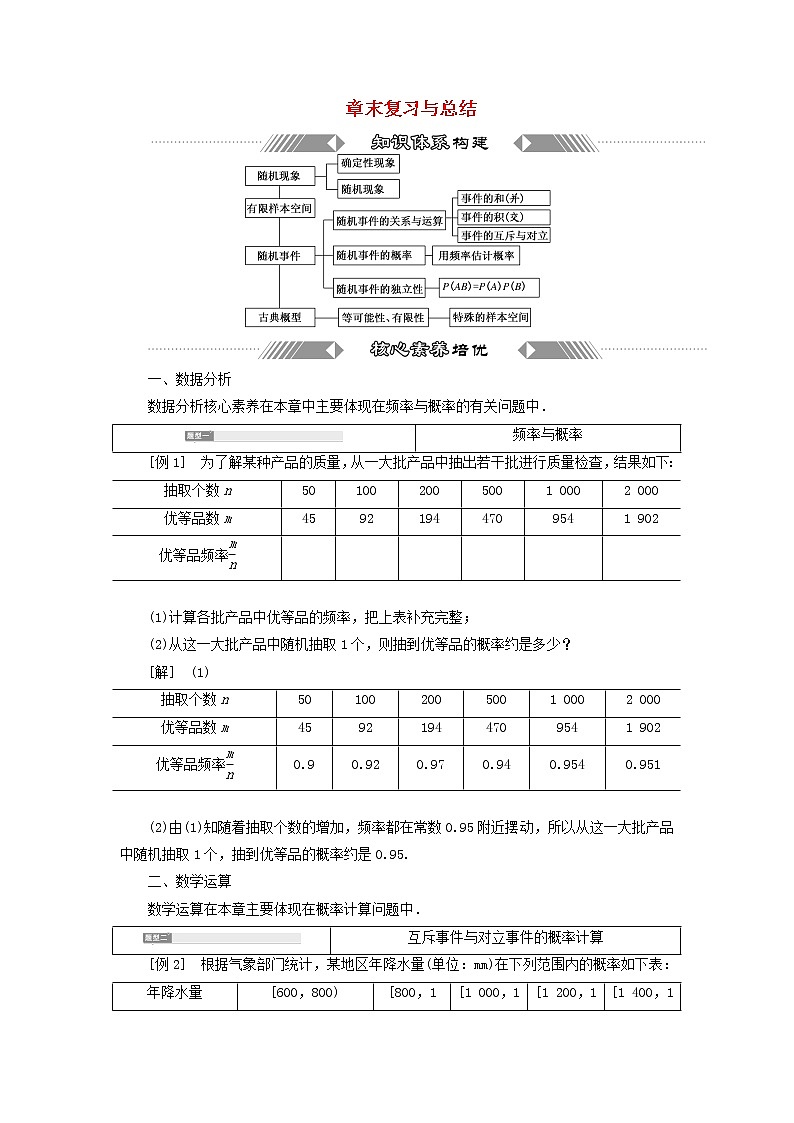
2021_2022学年新教材高中数学第七章概率章末复习与总结学案北师大版必修第一册
展开章末复习与总结
一、数据分析
数据分析核心素养在本章中主要体现在频率与概率的有关问题中.
频率与概率 |
[例1] 为了解某种产品的质量,从一大批产品中抽出若干批进行质量检查,结果如下:
抽取个数n | 50 | 100 | 200 | 500 | 1 000 | 2 000 |
优等品数m | 45 | 92 | 194 | 470 | 954 | 1 902 |
优等品频率 |
|
|
|
|
|
|
(1)计算各批产品中优等品的频率,把上表补充完整;
(2)从这一大批产品中随机抽取1个,则抽到优等品的概率约是多少?
[解] (1)
抽取个数n | 50 | 100 | 200 | 500 | 1 000 | 2 000 |
优等品数m | 45 | 92 | 194 | 470 | 954 | 1 902 |
优等品频率 | 0.9 | 0.92 | 0.97 | 0.94 | 0.954 | 0.951 |
(2)由(1)知随着抽取个数的增加,频率都在常数0.95附近摆动,所以从这一大批产品中随机抽取1个,抽到优等品的概率约是0.95.
二、数学运算
数学运算在本章主要体现在概率计算问题中.
互斥事件与对立事件的概率计算 |
[例2] 根据气象部门统计,某地区年降水量(单位:mm)在下列范围内的概率如下表:
年降水量 | [600,800) | [800,1 000) | [1 000,1 200) | [1 200,1 400) | [1 400,1 600] |
概率 | 0.12 | 0.26 | 0.38 | 0.16 | 0.08 |
(1)求年降水量在[800,1 200)范围内的概率;
(2)如果年降水量≥1 200 mm就可能发生涝灾,求该地区可能发生涝灾的概率.
[解] (1)记事件A为“年降水量在[800,1 000)”,B为“年降水量在[1 000,1 200)”,则所求事件为互斥事件A和B的并事件,所以年降水量在[800,1 200)范围内的概率是P(A∪B)=P(A)+P(B)=0.26+0.38=0.64.
(2)记事件C为“年降水量在[1 200,1 400)”,事件D为“年降水量在[1 400,1 600]”,则所求事件为互斥事件C和D的并事件,所以年降水量≥1 200 mm的概率是P(C∪D)=P(C)+P(D)=0.16+0.08=0.24.
古典概型的求法 |
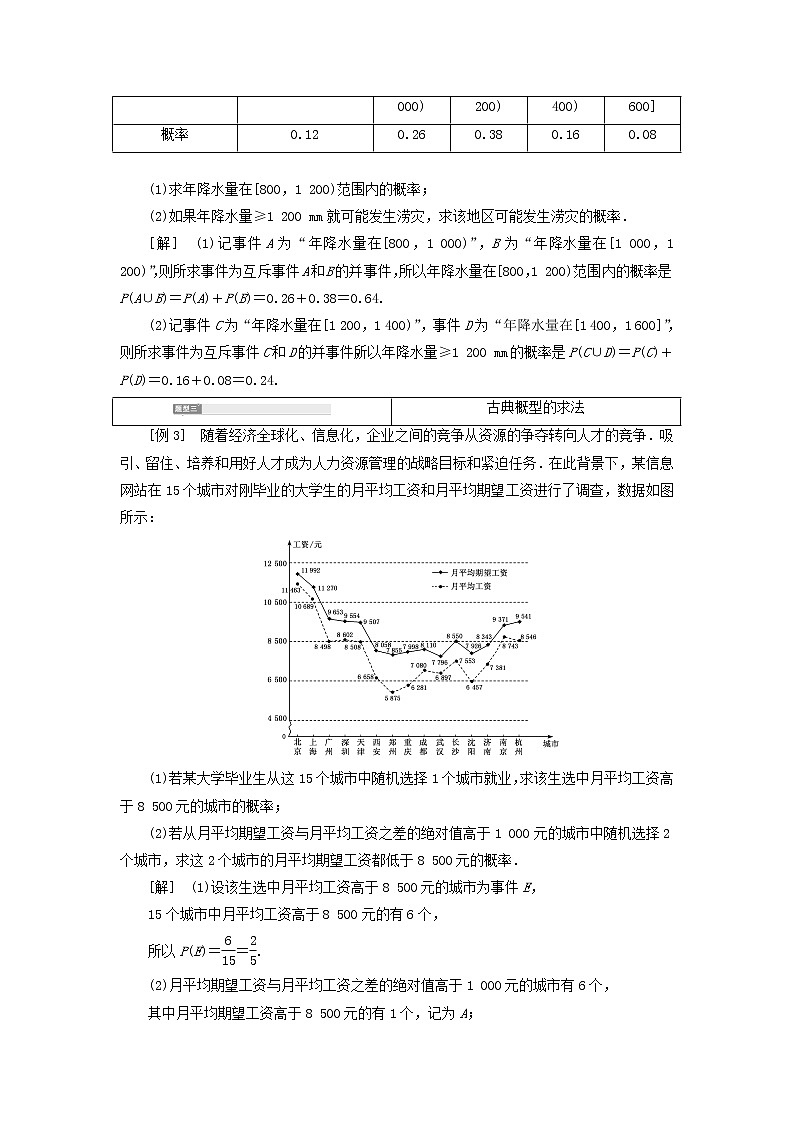
[例3] 随着经济全球化、信息化,企业之间的竞争从资源的争夺转向人才的竞争.吸引、留住、培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市对刚毕业的大学生的月平均工资和月平均期望工资进行了调查,数据如图所示:
(1)若某大学毕业生从这15个城市中随机选择1个城市就业,求该生选中月平均工资高于8 500元的城市的概率;
(2)若从月平均期望工资与月平均工资之差的绝对值高于1 000元的城市中随机选择2个城市,求这2个城市的月平均期望工资都低于8 500元的概率.
[解] (1)设该生选中月平均工资高于8 500元的城市为事件E,
15个城市中月平均工资高于8 500元的有6个,
所以P(E)==.
(2)月平均期望工资与月平均工资之差的绝对值高于1 000元的城市有6个,
其中月平均期望工资高于8 500元的有1个,记为A;
月平均期望工资低于8 500元的有5个,记为B1,B2,B3,B4,B5.
选取2个城市的所有可能情况为AB1,AB2,AB3,AB4,AB5,B1B2,B1B3,B1B4,B1B5,B2B3,B2B4,B2B5,B3B4,B3B5,B4B5,共15种,
其中2个城市的月平均期望工资都低于8 500元的有B1B2,B1B3,B1B4,B1B5,B2B3,B2B4,B2B5,B3B4,B3B5,B4B5,共10种.
所以所求概率为=.
事件的相互独立性 |
[例4] 计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书.甲、乙、丙三人在理论考试中“合格”的概率依次为,,,在实际操作考试中“合格”的概率依次为,,,所有考试是否合格相互之间没有影响.
(1)假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
(2)这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
[解] (1)设“甲获得合格证书”为事件A,“乙获得合格证书”为事件B,“丙获得合格证书”为事件C,则
P(A)=×=,P(B)=×=,
P(C)=×=.
因为P(C)>P(B)>P(A),所以丙获得合格证书的可能性最大.
(2)设“三人考试后恰有两人获得合格证书”为事件D,则
P(D)=P(AB)+P(AC)+P(BC)
=××+××+××=.
三、数学建模
数学建模核心素养在本章主要体现在概率的实际应用问题中.
概率的实际应用 |
[例5] 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:[40,50),[50,60),…,[80,90),[90,100].
(1)求频率分布直方图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60)的受访职工中,随机抽取2人,求此2人的评分都在[40,50)的概率.
[解] (1)因为(0.004+a+0.018+0.022×2+0.028)×10=1,所以a=0.006.
(2)由所给频率分布直方图知,50名受访职工评分不低于80的频率为(0.022+0.018)×10=0.4,
所以估计该企业的职工对该部门评分不低于80的概率为0.4.
(3)受访职工中评分在[50,60)的有50×0.006×10=3(人),记为A1,A2,A3;
受访职工中评分在[40,50)的有50×0.004×10=2(人),记为B1,B2.
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,即(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).
因为所抽取2人的评分都在[40,50)的结果有1种,即(B1,B2),所以所求的概率为.
[例6] 海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:
设两种养殖方法的箱产量相互独立,记A表示事件“旧养殖法的箱产量低于50 kg,新养殖法的箱产量不低于50 kg”,估计A的概率.
[解] 记B表示事件“旧养殖法的箱产量低于50 kg”,C表示事件“新养殖法的箱产量不低于50 kg”.
由题意知P(A)=P(BC)=P(B)P(C).
旧养殖法的箱产量低于50 kg的频率为(0.012+0.014+0.024+0.034+0.040)×5=0.62,
故P(B)的估计值为0.62.
新养殖法的箱产量不低于50 kg的频率为(0.068+0.046+0.010+0.008)×5=0.66,
故P(C)的估计值为0.66.
因此,事件A的概率估计值为0.62×0.66=0.409 2.









