人教版八年级下册第十七章 勾股定理综合与测试课堂检测

这是一份人教版八年级下册第十七章 勾股定理综合与测试课堂检测，共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．下列选项中不是勾股数的是（ ）
A．7，24，25B．4，5，6C．3，4，5D．9，12，15
2．如图，赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形两条直角边长分别为和，若，大正方形的边长为，则小正方形的面积为（ ）
A．B．C．D．
3．如图，在平面直角坐标系中，点P坐标为（﹣2，3），以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于（ ）
A．﹣4和﹣3之间B．﹣5和﹣4之间C．3和4之间D．4和5之间
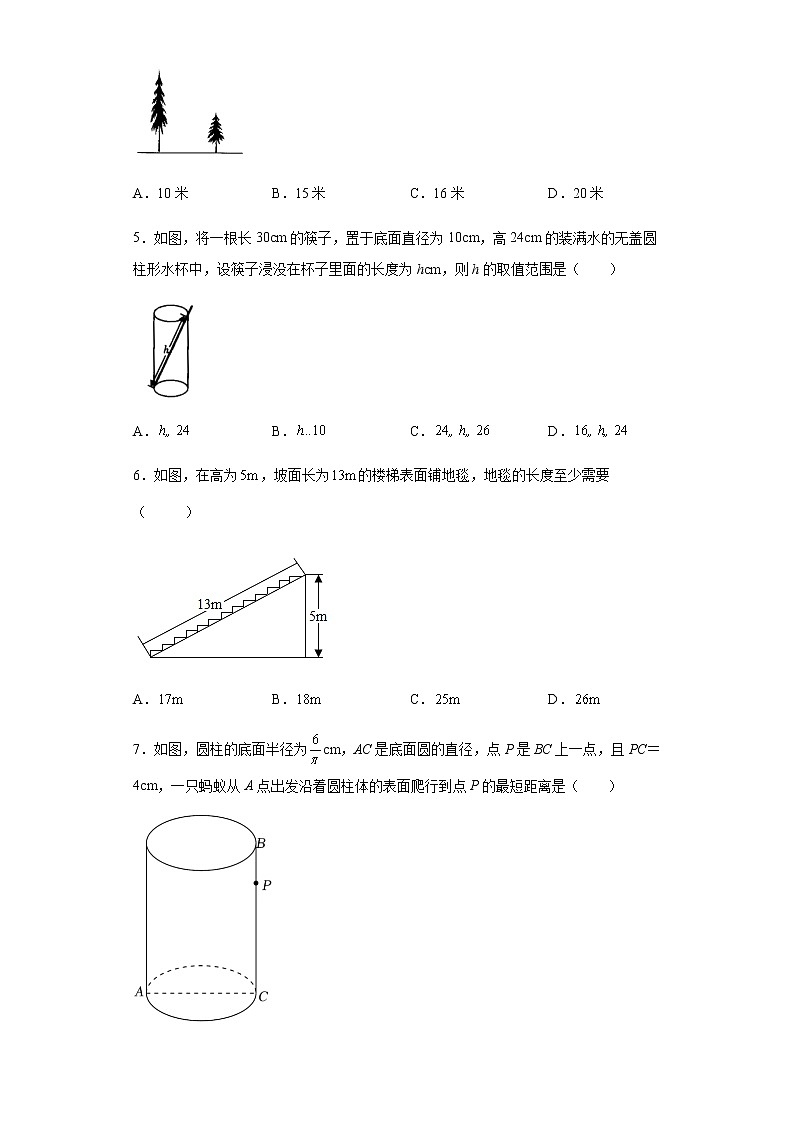
4．如图，有两棵树，一棵高19米，另一棵高10米，两树相距12米．若一只小鸟从一棵树的树梢飞到另一棵树的树梢，则小鸟至少飞行（ ）
A．10米B．15米C．16米D．20米
5．如图，将一根长30cm的筷子，置于底面直径为10cm，高24cm的装满水的无盖圆柱形水杯中，设筷子浸没在杯子里面的长度为hcm，则h的取值范围是（ ）
A．B．C．D．
6．如图，在高为，坡面长为的楼梯表面铺地毯，地毯的长度至少需要（ ）
A．B．C．D．
7．如图，圆柱的底面半径为cm，AC是底面圆的直径，点P是BC上一点，且PC＝4cm，一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是（ ）
A．4cmB．2cmC．5cmD．10cm
8．如果的三边分别为，且满足，则的面积为（ ）
A．6B．8C．10D．12
9．如图，点P是等边三角形ABC内一点，且PA＝3，PB＝4，PC＝5，则∠APB的度数是（ ）．
A．90°B．100°C．120°D．150°
二、填空题
10．已知点O（0，0），A（6，8），则线段AO的长度为______．
11．一个三角形的两边的长分别是3和5，要使这个三角形为直角三角形，则第三条边的长为_____．
12．如图，分别以此直角三角形的三边为直径在三角形外部画半圆，若S1＝9π，S2＝16π，则S3＝_____．
13．在一棵树的5米高B处有两个猴子为抢吃池塘边水果，一只猴子爬下树跑到A处（离树10米）的池塘边．另一只爬到树顶D后直接跃到A处，距离以直线计算，如果两只猴子所经过的距离相等，则这棵树高_______米.
14．《九章算术》中有一道“引葭赴岸”问题：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问水深，葭长各几何？”题意是：有一个池塘，其底面是边长为10尺的正方形，一棵芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B'（如图）．则芦苇长_____尺．
三、解答题
15．如图所示的一块地，，，，，，求这块地的面积．
16．如图，四边形ABCD中，AB=4，BC=3，CD=13，AD=12，∠B=90°．
(1)连接AC，求AC的长；
(2)求四边形ABCD的面积．
17．如图，连接四边形的对角线，已知，，，，．
(1)求证：是直角三角形；
(2)求四边形的面积．
18．如图，AD是△ABC的中线，DE⊥AC于点E，DF是△ABD的中线，且CE=2，DE=4，AE=8．
(1)求证：；
(2)求DF的长．
勾股定理章节巩固训练参考答案
1.【答案】B
2.【答案】A
3．【答案】A
4．【答案】B
5．【答案】C
6．【答案】A
7．【答案】B
8．【答案】A
9．【答案】D
二、填空题
10．【答案】10
11．【答案】4或
12．【答案】
13．【答案】
14．【答案】13
三、解答题
15．【答案】384
【详解】
解：连接，
在直角中，，，
由，解得，
在中，，，，
∵，
∴，
∴为直角三角形，
要求这块地的面积，求和的面积之差即可，
，
答：这块地的面积为．
16．【答案】(1)
(2)四边形的面积为36
【解析】
(1)
解：如图，连接
在中，由勾股定理得
∴的长为5．
(2)
解：∵，，
∴
∴是直角三角形
∴，∴
∴四边形的面积
∴四边形的面积为36．
17．【答案】(1)证明见详解（1）
(2)
【解析】
(1)
解：
∴△ABC是直角三角形，由勾股定理得：AC2=AB2＋BC2；
∴AC==2，
AD2=8，CD2=4，AC2=4，
AD2=AC2＋CD2,
∴△ACD是直角三角形；
(2)
解：SABCD=S△ABC＋S△ACD，
S△ABC==，S△ACD=，
∴SABCD=，
答：四边形的面积是：．
18．【答案】(1)见解析
(2)DF的长为5．
【解析】
(1)
证明：∵DE⊥AC于点E，
∴∠AED=∠CED=90°，
在Rt△ADE中，∠AED=90°，
∴AD2=AE2+DE2=82+42=80，
同理：CD2=20，
∴AD2+CD2=80+20=100，
∵AC=AE+CE=8+2=10，
∴AC2=100，
∴AD2+CD2=AC2，
∴△ADC是直角三角形，
∴∠ADC=90°；
(2)
解：∵AD是△ABC的中线，∠ADC=90°，
∴AD垂直平分BC，
∴AB=AC=10，
在Rt△ADB中，∠ADB=90°，
∵点F是边AB的中点，
∴DF=AB=5．
∴DF的长为5．