2021年九年级中考数学考点专题训练——专题十四：一次函数(含答案)

这是一份2021年九年级中考数学考点专题训练——专题十四：一次函数(含答案)，共38页。试卷主要包含了如图1，直线l等内容，欢迎下载使用。
备战2021中考数学考点专题训练——专题十四：一次函数
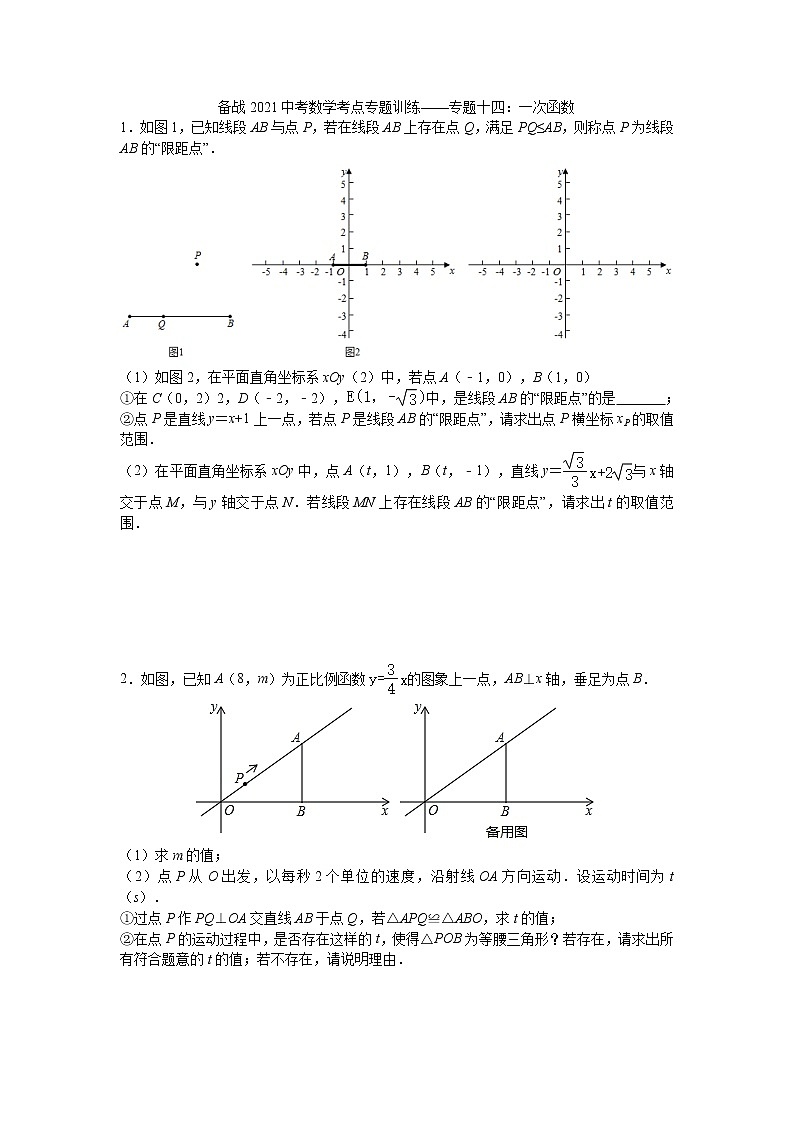
1．如图1，已知线段AB与点P，若在线段AB上存在点Q，满足PQ≤AB，则称点P为线段AB的“限距点”．

（1）如图2，在平面直角坐标系xOy（2）中，若点A（﹣1，0），B（1，0）
①在C（0，2）2，D（﹣2，﹣2），中，是线段AB的“限距点”的是　 　；
②点P是直线y＝x+1上一点，若点P是线段AB的“限距点”，请求出点P横坐标xP的取值范围．
（2）在平面直角坐标系xOy中，点A（t，1），B（t，﹣1），直线y＝与x轴交于点M，与y轴交于点N．若线段MN上存在线段AB的“限距点”，请求出t的取值范围．






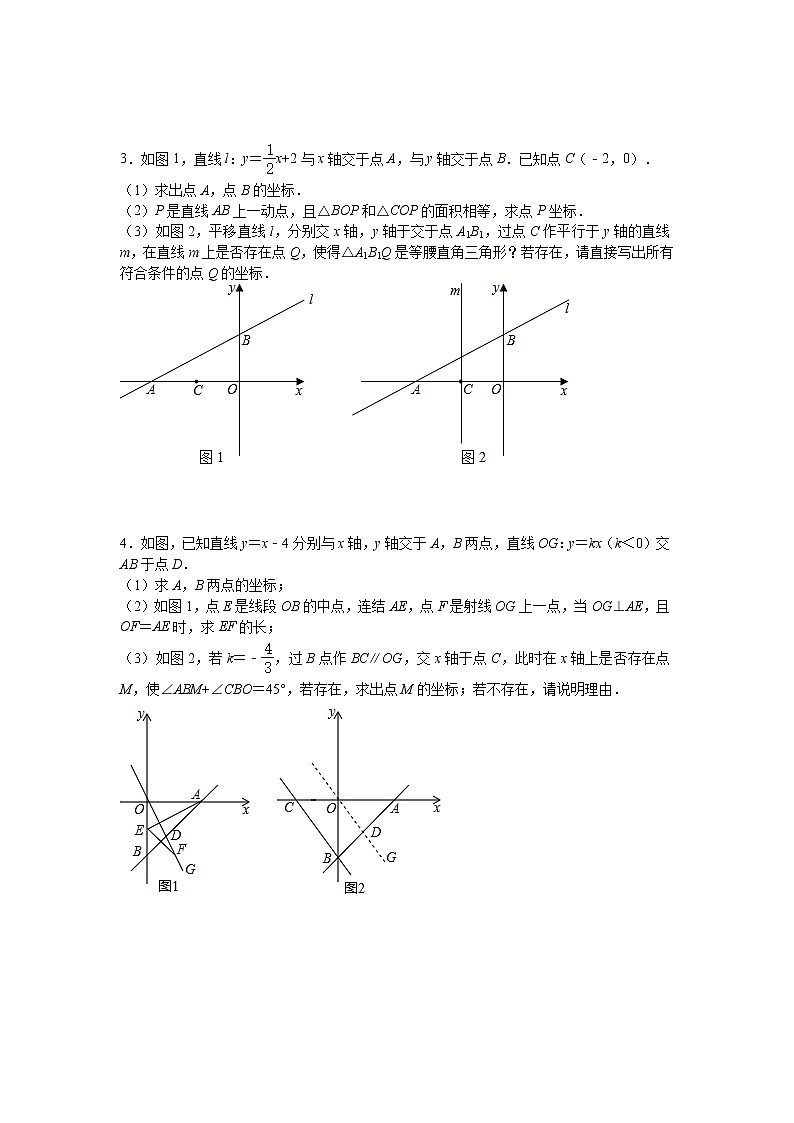
2．如图，已知A（8，m）为正比例函数的图象上一点，AB⊥x轴，垂足为点B．

（1）求m的值；
（2）点P从O出发，以每秒2个单位的速度，沿射线OA方向运动．设运动时间为t（s）．
①过点P作PQ⊥OA交直线AB于点Q，若△APQ≌△ABO，求t的值；
②在点P的运动过程中，是否存在这样的t，使得△POB为等腰三角形？若存在，请求出所有符合题意的t的值；若不存在，请说明理由．




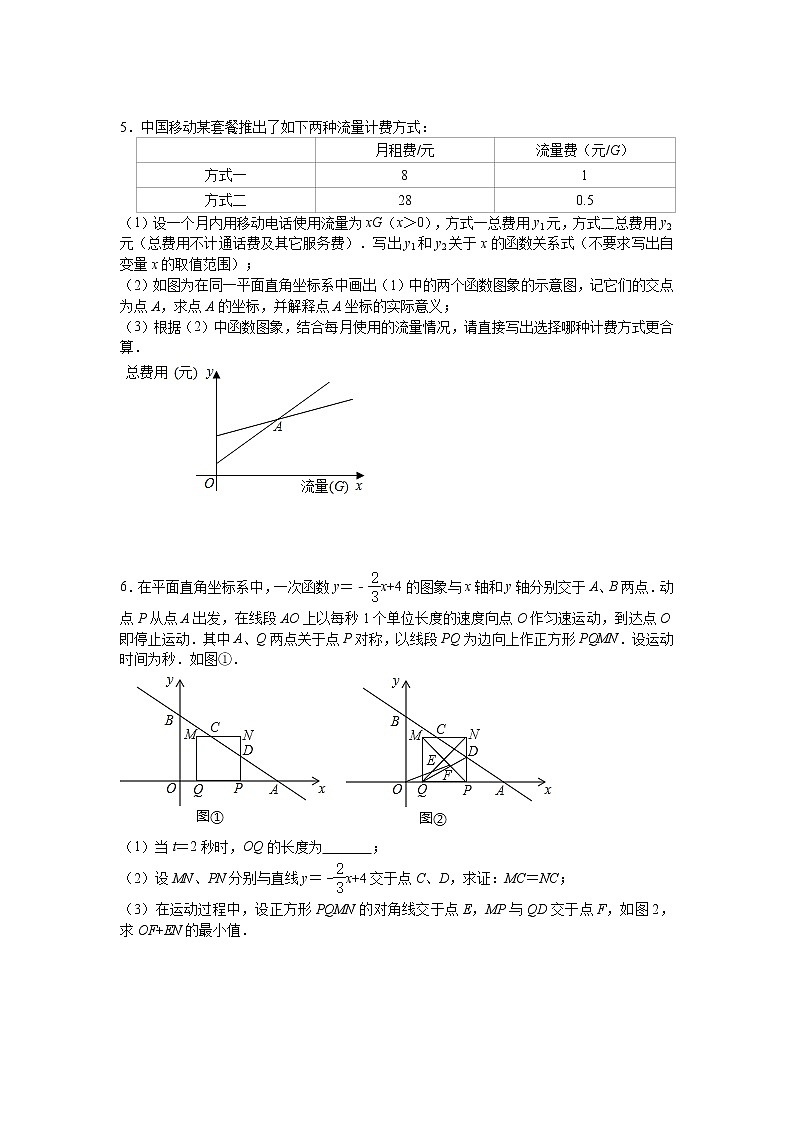
3．如图1，直线l：y＝x+2与x轴交于点A，与y轴交于点B．已知点C（﹣2，0）．
（1）求出点A，点B的坐标．
（2）P是直线AB上一动点，且△BOP和△COP的面积相等，求点P坐标．
（3）如图2，平移直线l，分别交x轴，y轴于交于点A1B1，过点C作平行于y轴的直线m，在直线m上是否存在点Q，使得△A1B1Q是等腰直角三角形？若存在，请直接写出所有符合条件的点Q的坐标．




4．如图，已知直线y＝x﹣4分别与x轴，y轴交于A，B两点，直线OG：y＝kx（k＜0）交AB于点D．
（1）求A，B两点的坐标；
（2）如图1，点E是线段OB的中点，连结AE，点F是射线OG上一点，当OG⊥AE，且OF＝AE时，求EF的长；
（3）如图2，若k＝﹣，过B点作BC∥OG，交x轴于点C，此时在x轴上是否存在点M，使∠ABM+∠CBO＝45°，若存在，求出点M的坐标；若不存在，请说明理由．







5．中国移动某套餐推出了如下两种流量计费方式：

月租费/元
流量费（元/G）
方式一
8
1
方式二
28
0.5
（1）设一个月内用移动电话使用流量为xG（x＞0），方式一总费用y1元，方式二总费用y2元（总费用不计通话费及其它服务费）．写出y1和y2关于x的函数关系式（不要求写出自变量x的取值范围）；
（2）如图为在同一平面直角坐标系中画出（1）中的两个函数图象的示意图，记它们的交点为点A，求点A的坐标，并解释点A坐标的实际意义；
（3）根据（2）中函数图象，结合每月使用的流量情况，请直接写出选择哪种计费方式更合算．




6．在平面直角坐标系中，一次函数y＝﹣x+4的图象与x轴和y轴分别交于A、B两点．动点P从点A出发，在线段AO上以每秒1个单位长度的速度向点O作匀速运动，到达点O即停止运动．其中A、Q两点关于点P对称，以线段PQ为边向上作正方形PQMN．设运动时间为秒．如图①．

（1）当t＝2秒时，OQ的长度为　 　；
（2）设MN、PN分别与直线y＝x+4交于点C、D，求证：MC＝NC；
（3）在运动过程中，设正方形PQMN的对角线交于点E，MP与QD交于点F，如图2，求OF+EN的最小值．





7．在平面直角坐标系xOy中，对于任意三点A，B，C的“矩积”，给出如下定义：
“横底”a：任意两点横坐标差的最大值；“纵高”h：任意两点纵坐标差的最大值；则“矩积”S＝ah．例如：三点坐标分别为A（1，﹣2），B（2，2），C（﹣1，﹣3），则“横底”a＝3，“纵高”h＝5，“矩积”S＝ah＝15．
已知点D（﹣2，3），E（1，﹣1）．
（1）若点F在x轴上．
①当D，E，F三点的“矩积”为24，则点F的坐标为　 　；
②直接写出D，E，F三点的“矩积”的最小值为　 　；
（2）若点F在直线y＝mx+4上，使得D，E，F三点的“矩积”取到最小值，直接写出m的取值范围是　 　．


8．如图，已知过点B（1，0）的直线l1与直线l2：y＝2x+4相交于点P（﹣1，a），l1与y轴交于点C，l2与x轴交于点A．

（1）求a的值及直线l1的解析式．
（2）求四边形PAOC的面积．
（3）在x轴上方有一动直线平行于x轴，分别与l1，l2交于点M，N，且点M在点N的右侧，x轴上是否存在点Q，使△MNQ为等腰直角三角形？若存在，请直接写出满足条件的点Q的坐标；若不存在，请说明理由．




9．如图1，已知直线AC的解析式为y＝﹣x+b，直线BC的解析式为y＝kx﹣2（k≠0），且△BOC的面积为6．

（1）求k和b的值；
（2）如图1，将直线AC绕A点逆时针旋转90°得到直线AD，点D在y轴上，若点M为x轴上的一个动点，点N为直线AD上的一个动点，当DM+MN+NB的值最小时，求此时点M的坐标及DM+MN+NB的最小值；
（3）如图2，将△AOD沿着直线AC平移得到△A′O′D′，A′D′与x轴交于点P，连接A′D、DP，当△DA′P是等腰三角形时，求此时P点坐标．










10．如图，四边形ABCD为平行四边形纸片．把纸片ABCD折叠，使点B恰好落在CD边上，折痕为AF．且AB＝10cm、AD＝8cm、DE＝6cm．
（1）求证：平行四边形ABCD是矩形；
（2）如图，以点B为坐标原点，水平方向、竖直方向为x轴、y轴建立平面直角坐标系，求直线AF的解析式；
（3）在（2）中的坐标系内是否存在这样的点P，使得以点P、A、E、F为顶点的四边形是平行四边形？若不存在，请说明理由；若存在，直接写出点P的坐标．





11．【模型建立】
（1）如图1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过A作AD⊥ED于点D，过B作BE⊥ED于点E．
求证：△BEC≌△CDA；
【模型应用】
（2）①已知直线l1：y＝x+8与坐标轴交于点A、B，将直线l1绕点A逆时针旋转45°至直线l2，如图2，求直线l2的函数表达式；
②如图3，长方形ABCO，O为坐标原点，点B的坐标为（8，﹣6），点A、C分别在坐标轴上，点P是线段BC上的动点，点D是直线y＝﹣3x+6上的动点且在y轴的右侧．若△APD是以点D为直角顶点的等腰直角三角形，请直接写出点D的坐标．




12．如图，A，B是直线y＝x+4与坐标轴的交点，直线y＝﹣2x+b过点B，与x轴交于点C．
（1）求A，B，C三点的坐标；
（2）当点D是AB的中点时，在x轴上找一点E，使ED+EB的和最小，画出点E的位置，并求E点的坐标．
（3）若点D是折线A﹣B﹣C上一动点，是否存在点D，使△ACD为直角三角形，若存在，直接写出D点的坐标；若不存在，请说明理由．










13．定义：在平面直角坐标系中，对于任意P（x1，y1），Q（x2，y2），若点M（x，y）满足x＝3（x1+x2），y＝3（y1+y2），则称点M是点P，Q的“美妙点”．例如：点P（1，2），Q（﹣2，1），当点M（x，y）满足x＝3×（1﹣2）＝﹣3，y＝3×（2+1）＝9时，则点M（﹣3，9）是点P，Q的“美妙点”．
（1）已知点A（﹣1，3），B（3，3），C（2，﹣2），请说明其中一点是另外两点的“美妙点”；
（2）如图，已知点D是直线y＝+2上的一点．点E（3，0），点M（x，y）是点D、E的“美妙点”．
①求y与x的函数关系式；
②若直线DM与x轴相交于点F，当△MEF为直角三角形时，求点D的坐标．






14．在平面直角坐标系xOy中，已知A（0，2），动点P在y＝x的图象上运动（不与O重合），连接AP．过点P作PQ⊥AP，交x轴于点Q，连接AQ．
（1）求线段AP长度的取值范围；
（2）试问：点P运动的过程中，∠QAP是否为定值？如果是，求出该值；如果不是，请说明理由．
（3）当△OPQ为等腰三角形时，求点Q的坐标．






15．如图1，已知直线AC：y＝﹣x+b1和直线AB：y＝kx+b2交于x轴上一点A，且分别交y轴于点C、点B，且OB＝2OC＝4．

（1）求k的值；
（2）如图1，点D是直线AB上一点，且在x轴上方，当S△ACD＝9时，在线段AC上取一点F，使得CF＝FA，点M，N分别为x轴、轴上的动点，连接NF，将△CNF沿NF翻折至△C′NF，求MD+MC′的最小值；
（3）如图2，H，P分别为射线AC，AO上的动点，连接PH，PC是否存在这样的点P，使得△PCH为等腰三角形，△PHA为直角三角形同时成立．请直接写出满足条件的点P坐标．




16．如图1，将一个长方形纸片AOBC放置在平面直角坐标系中，点O、A、B的坐标分别为（0，0）、（0，6）和（8，0），若点D是线段AB上的一个动点．
（1）点C的坐标为　 　；
（2）如果存在这样的点D，使得△BCD为等腰三角形，求出所有符合条件AD的长；
（3）点M在线段BC上，点N在直线y＝2x﹣6第一象限的图象上，若△AMN是等腰直角三角形，且∠ANM＝90°，请直接写出点N的坐标．





17．如图，在平面直角坐标系中，四边形OABC是矩形，点O（0，0），点A（3，0），点C（0，4）；D为AB边上的动点．
（Ⅰ）如图1，将△ABC对折，使得点B的对应点B落在对角线AC上，折痕为CD，求此刻点D的坐标：
（Ⅱ）如图2，将△ABC对折，使得点A的与点C重合，折痕交AB于点D，交AC于点E，求直线CD的解析式；
（Ⅲ）在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．




























备战2021中考数学考点专题训练——专题十四：一次函数参考答案
1．如图1，已知线段AB与点P，若在线段AB上存在点Q，满足PQ≤AB，则称点P为线段AB的“限距点”．

（1）如图2，在平面直角坐标系xOy（2）中，若点A（﹣1，0），B（1，0）
①在C（0，2）2，D（﹣2，﹣2），中，是线段AB的“限距点”的是　 　；
②点P是直线y＝x+1上一点，若点P是线段AB的“限距点”，请求出点P横坐标xP的取值范围．
（2）在平面直角坐标系xOy中，点A（t，1），B（t，﹣1），直线y＝与x轴交于点M，与y轴交于点N．若线段MN上存在线段AB的“限距点”，请求出t的取值范围．
【答案】解：（1）①∵点A（﹣1，0），B（1，0），
∴AB＝2，
∵点C到线段AB的最短距离是2≤AB，
∴点C是线段AB的“限距点”，
∵点D到线段AB的最短距离＝＝＞AB，
∴点D不是线段AB的“限距点”，
∵点E到线段AB的最短距离是≤AB，
∴点E是线段AB的“限距点”，
故答案为：C，E；
②∵点A（﹣1，0），B（1，0）
∴点P为线段AB的“限距点”的范围是平行于AB且到AB距离为2两条线段和以点A，点B为圆心，2为半径的两个半圆围成的封闭式图形，如图所示：

如图3，直线y＝x+1与该封闭式图形的交点为M，N，

∴点M坐标（1，2）
设点N（x，x+1）
∴（x+1）2+（x+1﹣0）2＝4
∴x＝﹣1﹣
∴，
∴点P横坐标xP的取值范围为：；
（2）∵直线y＝与x轴交于点M，与y轴交于点N．
∴点N（0，2），点M（﹣6，0）
如图3，线段AB的“限距点”的范围所形成的图形与线段MN交于点M，

∵点M是线段AB的“限距点”，
∴﹣6﹣t＝2，
∴t＝﹣8，
若线段AB的“限距点”的范围所形成的图形与线段MN相切于点F，延长B'A'交MN于E，

∵sin∠FEA'＝sin∠MNO，
∴＝
∴
∴t＝﹣2，
∴t的取值范围为﹣8≤t≤﹣2．
2．如图，已知A（8，m）为正比例函数的图象上一点，AB⊥x轴，垂足为点B．

（1）求m的值；
（2）点P从O出发，以每秒2个单位的速度，沿射线OA方向运动．设运动时间为t（s）．
①过点P作PQ⊥OA交直线AB于点Q，若△APQ≌△ABO，求t的值；
②在点P的运动过程中，是否存在这样的t，使得△POB为等腰三角形？若存在，请求出所有符合题意的t的值；若不存在，请说明理由．
【答案】解：（1）∵A（8，m）在正比例函数的图象上，
∴当x＝8时，y＝6，
∴m的值为6；
（2）∵A（8，6），
∴OA＝10，
①若△APQ≌△ABO，则AP＝AB＝6．
当点P在线段OA上时，得OP＝4，即2t＝4，解得t＝2；
当点P在线段OA的延长线上时，得OP＝16，即2t＝16，解得t＝8；
②若PO＝PB，则点P在OB的垂直平分线上，此时OP＝5，即2t＝5，
∴t＝2.5；
若OP＝OB，则OP＝8，即2t＝8，
∴t＝4；
若BP＝BO，则可得OP＝12.8，即2t＝12.8，
∴t＝6.4．
综上可得当t的值为2.5或4或6.4时，△POB为等腰三角形．
3．如图1，直线l：y＝x+2与x轴交于点A，与y轴交于点B．已知点C（﹣2，0）．
（1）求出点A，点B的坐标．
（2）P是直线AB上一动点，且△BOP和△COP的面积相等，求点P坐标．
（3）如图2，平移直线l，分别交x轴，y轴于交于点A1B1，过点C作平行于y轴的直线m，在直线m上是否存在点Q，使得△A1B1Q是等腰直角三角形？若存在，请直接写出所有符合条件的点Q的坐标．

【答案】解：（1）设y＝0，则x+2＝0，
解得：x＝﹣4，
设x＝0，则y＝2，
∴点A的坐标为（﹣4，0），点B的坐标的坐标为（0，2）；
（2）∵点C（﹣2，0），点B（0，2），
∴OC＝2，OB＝2，
∵P是直线AB上一动点，
∴设P（m，m+2），
∵△BOP和△COP的面积相等，
∴×2|m|＝2×（|m|+2），
解得：m＝±4，
当m＝﹣4时，点P与点A重合，
∴点P坐标为（4，4）；
（3）存在；
理由：如图1，

①当点B1是直角顶点时，
∴B1Q＝B1A1，
∵∠A1B1O+∠QB1H＝90°，∠A1B1O+∠OA1B1＝90°，
∴∠OA1B1＝∠QB1H，
在△A1OB1和△B1HQ中，，
∴△A1OB1≌△B1HQ（AAS），
∴B1H＝A1O，OB1＝HQ＝2，
∴B1（0，﹣2）或（0，2），
当点B1（0，﹣2）时，Q（﹣2，2），
当点B1（0，2）时，
∵B（0，2），
∴点B1（0，2）（不合题意舍去），
∴直线AB向下平移4个单位，
∴点Q也向上平移4个单位，
∴Q（﹣2，2），
②当点A1是直角顶点时，A1B1＝A1Q，



∵直线AB的解析式为y＝x+2，
由平移知，直线A1B1的解析式为y＝x+b，
∴A1（﹣2b，0），B1（0，b），
∴A1B12＝4b2+b2＝5b2，
∵A1B1⊥A1Q，
∴直线A1Q的解析式为y＝﹣2x﹣4b
∴Q（﹣2，4﹣4b），
∴A1Q2＝（﹣2b+2）2+（4﹣4b）2＝20b2+40b+20，
∴20b2﹣40b+20＝5b2，
∴b＝2或b＝，
∴Q（﹣2，﹣4）或（﹣2，）；
③当Q是直角顶点时，过Q作QH⊥y轴于H，

∴A1Q＝B1Q，
∵∠QA1C1+∠A1QC＝90°，∠A1QC+∠CQB1＝90°，
∴∠QA1C＝∠CQB1，
∵m∥y轴，
∴∠CQB1＝∠QB1H，
∴∠QA1C＝∠QB1H
在△A1QC与△B1QH中，，
∴△A1QC≌△B1QH（AAS），
∴CQ＝QH＝2，B1H＝A1C，
∴Q（﹣2，2）或（﹣2，﹣2），
即：满足条件的点Q为（﹣2，2）或（﹣2，﹣2）或（﹣2，12）或（﹣2，）．
4．如图，已知直线y＝x﹣4分别与x轴，y轴交于A，B两点，直线OG：y＝kx（k＜0）交AB于点D．
（1）求A，B两点的坐标；
（2）如图1，点E是线段OB的中点，连结AE，点F是射线OG上一点，当OG⊥AE，且OF＝AE时，求EF的长；
（3）如图2，若k＝﹣，过B点作BC∥OG，交x轴于点C，此时在x轴上是否存在点M，使∠ABM+∠CBO＝45°，若存在，求出点M的坐标；若不存在，请说明理由．

【答案】解：（1）∵直线y＝x﹣4分别与x轴，y轴交于A，B两点，
∴令y＝0，则x﹣4＝0，
∴x＝4，
令x＝0，则y＝﹣4，
∴A（4，0），B（0，﹣4）；
（2）∵A（4，0），B（0，﹣4），
∴OA＝OB＝4，
∵点E是线段OB的中点，
∴OE＝2，
过F作FB′⊥y轴于B′，
∴∠AOE＝∠OB′F＝90°，
∵OG⊥AE，
∴∠OAE+∠AOF＝∠B′OG+∠AOF＝90°，
∴∠OAE＝∠B′OF，
∵OF＝AE，
∴△AOE≌△OB′F（AAS），
∴FB＝OE＝2，OB′＝OA＝4，
∵OB＝4，
∴点B与点B′重合，
∴EF＝＝＝2；
（3）存在，∵k＝﹣，
∴直线OG：y＝﹣x（k＜0），
∵BC∥OG，
∴设直线BC的解析式为y＝﹣x﹣4，
当y＝0时，即﹣x﹣4＝0，
∴x＝﹣3，
∴C（﹣3，0），
如图，当点M在点A的左侧，
∵∠ABO＝45°，∠ABM+∠CBO＝45°，
∴∠MBO＝∠CBO，
∵∠COB＝∠NOB＝90°，OB＝OB，
∴△BCO≌△BMO（ASA），
∴OM＝OC＝3，
∴M（3，0）；
当点M在点A的右侧时，
∵∠OAB＝∠AM′B+∠ABM′＝45°，∠ABM+∠CBO＝45°，
∴∠AM′B＝∠OBC，
∵∠CBO＝∠M′OB，
∴∠COB+∠OBM′＝90°，
设OM′＝a，
∴BM′＝，
∵S△CBM′＝OB×CM′＝BC•BM′，
∴4×（3+a）＝×，
解得：a＝，
∴M′（，0），
综上所述，点M的坐标为：（3，0），（，0）．


5．中国移动某套餐推出了如下两种流量计费方式：

月租费/元
流量费（元/G）
方式一
8
1
方式二
28
0.5
（1）设一个月内用移动电话使用流量为xG（x＞0），方式一总费用y1元，方式二总费用y2元（总费用不计通话费及其它服务费）．写出y1和y2关于x的函数关系式（不要求写出自变量x的取值范围）；
（2）如图为在同一平面直角坐标系中画出（1）中的两个函数图象的示意图，记它们的交点为点A，求点A的坐标，并解释点A坐标的实际意义；
（3）根据（2）中函数图象，结合每月使用的流量情况，请直接写出选择哪种计费方式更合算．

【答案】解：（1）y1＝x+8，；

（2）由题意得，
解之，得
即点A的坐标为（40，48）．
点A的坐标的实际意义为当每月使用的流量为40G时，两种计费方式的总费用一样多，都为48元．

（3）当每月使用的流量少于40G时，选择方式一更省钱；
当每月使用的流量等于40G时，两种方式的总费用都一样；
当每月使用的流量大于40G时，选择方式二更省钱．
6．在平面直角坐标系中，一次函数y＝﹣x+4的图象与x轴和y轴分别交于A、B两点．动点P从点A出发，在线段AO上以每秒1个单位长度的速度向点O作匀速运动，到达点O即停止运动．其中A、Q两点关于点P对称，以线段PQ为边向上作正方形PQMN．设运动时间为秒．如图①．

（1）当t＝2秒时，OQ的长度为　 　；
（2）设MN、PN分别与直线y＝x+4交于点C、D，求证：MC＝NC；
（3）在运动过程中，设正方形PQMN的对角线交于点E，MP与QD交于点F，如图2，求OF+EN的最小值．
【答案】解：（1）在y＝﹣x+4中，令y＝0，得x＝6，
∴OA＝6，
∵t＝2，
∴AP＝PQ＝2，
∴OQ＝6﹣2﹣2＝2，
故答案为：2；

（2）∵AP＝PQ＝t，
∴OQ＝6﹣2t，
∵四边形PQMN是正方形，
∴PQ＝QM＝MN＝PN＝t，
∴M（6﹣2t，t），N（6﹣t，t），C（6﹣t，t），
∴CM＝（6﹣t）﹣（6﹣2t）＝t，
CN＝（6﹣t）﹣（6﹣t）＝t，
∴CM＝CN；

（3）作矩形NEFK，则EN＝FK，
∵OF+EN＝OF+FK，
∴当O，F，K三点共线时，OF+EN＝OF+FK的值最小，如图，
作OH⊥QN于H，
在等腰直角三角形PQN中，∵PQ＝t，
∴QN＝t，
∴HN＝QN﹣QH＝t﹣（t﹣3）＝3，
∴OF+EN的最小值为：HE+EN＝HN＝3．

7．在平面直角坐标系xOy中，对于任意三点A，B，C的“矩积”，给出如下定义：
“横底”a：任意两点横坐标差的最大值；“纵高”h：任意两点纵坐标差的最大值；则“矩积”S＝ah．例如：三点坐标分别为A（1，﹣2），B（2，2），C（﹣1，﹣3），则“横底”a＝3，“纵高”h＝5，“矩积”S＝ah＝15．
已知点D（﹣2，3），E（1，﹣1）．
（1）若点F在x轴上．
①当D，E，F三点的“矩积”为24，则点F的坐标为　 　；
②直接写出D，E，F三点的“矩积”的最小值为　 　；
（2）若点F在直线y＝mx+4上，使得D，E，F三点的“矩积”取到最小值，直接写出m的取值范围是　 　．

【答案】解：（1）设点F（a，0），
①∵D，E，F三点的“矩积”为24，“纵高”＝4，
∴横底”＝6，
若a＜﹣2，则1﹣a＝6，
∴a＝﹣5；
若﹣2≤a≤1，则1﹣（﹣2）＝3≠6，不合题意舍去；
若a＞1，则a﹣（2）＝6；
∴a＝4，
∴点F（﹣5，0）或（4，0），
故答案为（﹣5，0）或（4，0）；
②当若a＜﹣2，则1﹣a＞3，
∴S＝4（1﹣a）＞12，
当﹣2≤a≤1时，S＝3×4＝12，
当a＞1时，则a﹣（﹣2）＞3，
∴S＝4×[a﹣（﹣2）]＞12，
∴D，E，F三点的“矩积”的最小值为12，
故答案为12；
（2）设点F（a，0），
由（1）可知：当﹣2≤a≤1时，D，E，F三点的“矩积”能取到最小值，
如图，

当直线y＝mx+4过点D（﹣2，3）时，
∴3＝﹣2m+4，
∴m＝，
当直线y＝mx+4过点H（1，3）时，
∴3＝m+4，
∴m＝﹣1，
∴当m≥或m≤﹣1时，D，E，F三点的“矩积”能取到最小值．
8．如图，已知过点B（1，0）的直线l1与直线l2：y＝2x+4相交于点P（﹣1，a），l1与y轴交于点C，l2与x轴交于点A．

（1）求a的值及直线l1的解析式．
（2）求四边形PAOC的面积．
（3）在x轴上方有一动直线平行于x轴，分别与l1，l2交于点M，N，且点M在点N的右侧，x轴上是否存在点Q，使△MNQ为等腰直角三角形？若存在，请直接写出满足条件的点Q的坐标；若不存在，请说明理由．
【答案】解：（1）∵y＝2x+4过点P（﹣1，a），
∴a＝2，
∵直线l1过点B（1，0）和点P（﹣1，2），
设线段BP所表示的函数表达式y＝kx+b并解得：
函数的表达式y＝﹣x+1；

（2）过点P作PE⊥OA于点E，作PF⊥y轴交y轴于点F，

则；

（3）如图，M（1﹣a，a），点N，
∵MN＝NQ，则，

①当MN＝NQ时，
②当MN＝MQ时，Q2（﹣，0），
③当MQ＝NQ时，，
∴，∴Q3（﹣，0）．
综上，点Q的坐标为：（﹣，0）或（﹣，0）或（﹣，0）．
9．如图1，已知直线AC的解析式为y＝﹣x+b，直线BC的解析式为y＝kx﹣2（k≠0），且△BOC的面积为6．

（1）求k和b的值；
（2）如图1，将直线AC绕A点逆时针旋转90°得到直线AD，点D在y轴上，若点M为x轴上的一个动点，点N为直线AD上的一个动点，当DM+MN+NB的值最小时，求此时点M的坐标及DM+MN+NB的最小值；
（3）如图2，将△AOD沿着直线AC平移得到△A′O′D′，A′D′与x轴交于点P，连接A′D、DP，当△DA′P是等腰三角形时，求此时P点坐标．
【答案】解：（1）直线BC的解析式为y＝kx﹣2，则点C（0，﹣2），
将点C的坐标代入y＝﹣x+b得：﹣2＝b，解得：b＝﹣2，
故直线AC的表达式为：y＝﹣x﹣2；
△BOC的面积＝OB•CO＝2×OB＝6，解得：OB＝6，
故点B（6，0），
将点B的坐标代入y＝kx﹣2得：0＝6k﹣2，解得：k＝；
故k＝，b＝﹣2；

（2）将直线AC绕A点逆时针旋转90°得到直线AD，则点D（0，2），
由点A、D的坐标得，直线AD的表达式为：y＝x+2；
过点B作点B关于直线AD的对称点B′，连接B′C交AD于点N，交x轴于点M，则点M、N为所求点，

点C是点D关于x轴的对称点，则MC＝MD，而NB＝NB′，
故DM+MN+NB＝MC+MN+NB′＝B′C为最小，
直线AD的倾斜角为45°，BB′⊥AD，则AB＝AB′＝8，
直线AB′与AD的夹角也为45°，故直线AB′⊥AB，故点B′（﹣2，8），
由点B′、C的坐标得，直线B′C的表达式为：y＝﹣5x﹣2，
令y＝0，即﹣5x﹣2＝0，解得：x＝﹣，
故点M（﹣，0），
DM+MN+NB最小值为B′C＝＝2；

（3）设△AOD沿着直线AC向右平移m个单位，向下平移m个单位得到△A′O′D′，则点A′（m﹣2，﹣m），
设直线A′D′的表达式为：y＝x+b′，将点A′的坐标代入上式得：
﹣m＝m﹣2+b′，解得：b′＝2﹣2m，
则直线A′D′的表达式为：y＝x+2﹣2m，
令y＝0，则x＝2m﹣2，故点P（2m﹣2，0），而点A′（m﹣2，﹣m），点D（0，2），
则A′P2＝2m2，A′D2＝（m﹣2）2+（﹣m﹣2）2＝2m2+8，PD2＝（2m﹣2）2+4；
当A′P＝A′D时，2m2＝2m2+8，解得：方程无解；
当A′P＝PD时，同理可得：m＝2；
当A′D＝PD时，同理可得：m＝0（舍去）或4，
综上，点P（2，0）或（6，0）．
10．如图，四边形ABCD为平行四边形纸片．把纸片ABCD折叠，使点B恰好落在CD边上，折痕为AF．且AB＝10cm、AD＝8cm、DE＝6cm．
（1）求证：平行四边形ABCD是矩形；
（2）如图，以点B为坐标原点，水平方向、竖直方向为x轴、y轴建立平面直角坐标系，求直线AF的解析式；
（3）在（2）中的坐标系内是否存在这样的点P，使得以点P、A、E、F为顶点的四边形是平行四边形？若不存在，请说明理由；若存在，直接写出点P的坐标．

【答案】解：（1）证明：∵把纸片ABCD折叠，使点B恰好落在CD边上，
∴AE＝AB＝10，AE2＝102＝100，
又∵AD2+DE2＝82+62＝100，
∴AD2+DE2＝AE2，
∴△ADE是直角三角形，且∠D＝90°，
又∵四边形ABCD为平行四边形，
∴平行四边形ABCD是矩形（有一个角是直角的平行四边形是矩形）；

（2）设BF＝x，则EF＝BF＝x，EC＝CD﹣DE＝10﹣6＝4cm，FC＝BC﹣BF＝8﹣x，
在Rt△EFC中，EC2+FC2＝EF2，
即42+（8﹣x）2＝x2，
解得：x＝5，故BF＝5cm，则点E（8，4），
则点F（5，0）、而点A（0，10），
将点A、F的坐标代入一次函数表达式：y＝kx+b并解得：
直线AF的表达式为：y＝﹣2x+10；

（3）存在，理由：
设点P（a，b），点A、F、E的坐标分别为：（0，10）、（5，0）、（8，4），
①当AF是平行四边形的一条边时，
点A向下平移10个单位向右平移5个单位得到F，
同样点E（P）向下平移10个单位向右平移5个单位得到P（E），
即：8﹣10＝a，4+5＝b或8+10＝a，4﹣5＝b，
解得：a＝﹣2，b＝9或a＝18，b＝﹣1，
②当AF是平行四边形的对角线时，
由中点公式得：0+5＝a+8，10+0＝4+b，
解得：a＝﹣3，b＝6；
综上点P的坐标为：（﹣2，9）或（18，﹣1）或（﹣3，6）．
11．【模型建立】
（1）如图1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过A作AD⊥ED于点D，过B作BE⊥ED于点E．
求证：△BEC≌△CDA；
【模型应用】
（2）①已知直线l1：y＝x+8与坐标轴交于点A、B，将直线l1绕点A逆时针旋转45°至直线l2，如图2，求直线l2的函数表达式；
②如图3，长方形ABCO，O为坐标原点，点B的坐标为（8，﹣6），点A、C分别在坐标轴上，点P是线段BC上的动点，点D是直线y＝﹣3x+6上的动点且在y轴的右侧．若△APD是以点D为直角顶点的等腰直角三角形，请直接写出点D的坐标．

【答案】解：（1）∵∠EBC+∠ECB＝90°，∠ECB+∠ACD＝90°，
∴∠ACD＝∠BCE，∠ADC＝∠BEC＝90°，CB＝CA，
∴△BEC≌△CDA（AAS）；

（2）①直线l1：y＝x+8与坐标轴交于点A、B，则点A、B的坐标分别为：（﹣6，0）、（0，8），
则AO＝6，OB＝8，
如图2，过点B作CB⊥AB交l2于点C，过点C作CH⊥y轴于点H，

由（1）知：△CHB≌△BOA（AAS），
∴CH＝OB＝8，HB＝OA，故点C（﹣8，14），
将点A、C的坐标代入一次函数表达式：y＝kx+b并解得：
l2的表达式为：y＝﹣7x﹣42；
②点D在y＝﹣3x+6上，设点D（m，﹣3m+6），
过点D作x轴的平行线交y轴于点M，交CB的延长线于点N，

则△DMA≌△PND（AAS），
∴AM＝PN，即8﹣m＝|﹣6+3m﹣6|，
解得：m＝2或5；
故点D的坐标为：（2，0）或（5，﹣9）．
12．如图，A，B是直线y＝x+4与坐标轴的交点，直线y＝﹣2x+b过点B，与x轴交于点C．
（1）求A，B，C三点的坐标；
（2）当点D是AB的中点时，在x轴上找一点E，使ED+EB的和最小，画出点E的位置，并求E点的坐标．
（3）若点D是折线A﹣B﹣C上一动点，是否存在点D，使△ACD为直角三角形，若存在，直接写出D点的坐标；若不存在，请说明理由．

【答案】解：（1）在y＝x+4中，
令x＝0，得y＝4，
令y＝0，得x＝﹣4，∴A（﹣4，0），B（0，4）．
把B（0，4）代入，y＝﹣2x+b，
得b＝4
∴直线BC为：y＝﹣2x+4．
在y＝﹣2x+4中，
令y＝0，得x＝2，
∴C点的坐标为（2，0）；

（2）如图点E为所求
点D是AB的中点，A（﹣4，0），B（0，4）．∴D（﹣2，2）．
点B关于x轴的对称点B1的坐标为（0，﹣4）．
设直线DB1的解析式为y＝kx+b．
把D（﹣2，2），B1（0，﹣4）代入一次函数表达式并解得：
故该直线方程为：y＝﹣3x﹣4．
令y＝0，得E点的坐标为（﹣，0）．


（3）存在，D点的坐标为（﹣1，3）或．
①当点D在AB上时，由OA＝OB＝4
得到：∠BAC＝45°，
由等腰直角三角形求得D点的坐标为（﹣1，3）；
②当点D在BC上时，如图，设AD交y轴于点F．

在△AOF与△BOC中，∠FAO＝∠CBO，∠AOF＝∠BOD，AO＝BO，
∴△AOF≌△BOC（ASA）．∴OF＝OC＝2，
∴点F的坐标为（0，2），
易得直线AD的解析式为，与y＝﹣2x+4组成方程组并解得：
x＝，∴交点D的坐标为．
13．定义：在平面直角坐标系中，对于任意P（x1，y1），Q（x2，y2），若点M（x，y）满足x＝3（x1+x2），y＝3（y1+y2），则称点M是点P，Q的“美妙点”．例如：点P（1，2），Q（﹣2，1），当点M（x，y）满足x＝3×（1﹣2）＝﹣3，y＝3×（2+1）＝9时，则点M（﹣3，9）是点P，Q的“美妙点”．
（1）已知点A（﹣1，3），B（3，3），C（2，﹣2），请说明其中一点是另外两点的“美妙点”；
（2）如图，已知点D是直线y＝+2上的一点．点E（3，0），点M（x，y）是点D、E的“美妙点”．
①求y与x的函数关系式；
②若直线DM与x轴相交于点F，当△MEF为直角三角形时，求点D的坐标．

【答案】解：（1）∵3×（﹣1+2）＝3，3×（3﹣2）＝3，
∴点B是A、C的“美妙点”；

（2）设点D（m，m+2），
①∵M是点D、E的“美妙点”．
∴x＝3（3+m）＝9+3m，y＝3（0+m+2）＝m+6，
故m＝x﹣3，
∴y＝（x﹣3）+6＝x+3；

②由①得，点M（9+3m，m+6），
如图1，当∠MEF为直角时，则点M（3，4），
∴9+3m＝3，解得：m＝﹣2；
∴点D（﹣2，）；

当∠MFE是直角时，如图2，
则9+3m＝m，解得：m＝﹣，
∴点D（﹣，）；
当∠EMF是直角时，
同理可得：点D（﹣，）或（﹣，），
综上，点D（﹣2，）或（﹣，）或（﹣，）或（﹣，）．
14．在平面直角坐标系xOy中，已知A（0，2），动点P在y＝x的图象上运动（不与O重合），连接AP．过点P作PQ⊥AP，交x轴于点Q，连接AQ．
（1）求线段AP长度的取值范围；
（2）试问：点P运动的过程中，∠QAP是否为定值？如果是，求出该值；如果不是，请说明理由．
（3）当△OPQ为等腰三角形时，求点Q的坐标．

【答案】解：（1）如图1，作AH⊥OP，则AP≥AH，

∵点P在y＝x的图象上
∴∠HOQ＝30°，∠HOA＝60°
∵A（0，2）
∴AH＝AO•sin60°＝
∴AP≥
（2）
①当点P在第三象限时，如图2，

由∠QPA＝∠QOA＝90°，可得Q、P、O、A四点共圆，
∴∠PAQ＝∠POQ＝30°
②当点P在第一象限的线段OH上时，如图3
由∠QPA＝∠QOA＝90°可得Q、P、O、A四点共圆
∴∠PAQ+∠POQ＝180°，又此时∠POQ＝150°
∴∠PAQ＝180°﹣∠POQ＝30°
③当点P在第一象限的线段OH的延长线上时，
由∠QPA＝∠QOA＝90°可得∠APQ+∠AOQ＝180°
∴Q、P、O、A四点共圆
∴∠PAQ＝∠POQ＝30°
（3）设P（m，m），则lAP：y＝x+2，
∵PQ⊥AP
∴kPQ＝
∴lPQ：y＝（x﹣m）+m
∴Q（，0）
∴OP2＝m2，OQ2＝m2﹣m+
PQ2＝m2﹣m+
①OP＝OQ时，则m2＝m2﹣m+
整理得：m2﹣4m+3＝0
解得m＝2±3
∴Q1（2+4，0），Q2（2﹣4，0）
②当PO＝PQ时，则m2＝m2﹣m+
整理得：2m2+
解得：m＝或m＝﹣
当m＝时，Q点与O重合，舍去，
∴m＝﹣
∴Q3（﹣2，0）
③当QO＝QP时，
则
整理得：m2﹣
解得：m＝
∴Q4（）
∴点Q的坐标为（2+4，0）或（2﹣4，0）或（﹣2，0）或（）．
15．如图1，已知直线AC：y＝﹣x+b1和直线AB：y＝kx+b2交于x轴上一点A，且分别交y轴于点C、点B，且OB＝2OC＝4．

（1）求k的值；
（2）如图1，点D是直线AB上一点，且在x轴上方，当S△ACD＝9时，在线段AC上取一点F，使得CF＝FA，点M，N分别为x轴、轴上的动点，连接NF，将△CNF沿NF翻折至△C′NF，求MD+MC′的最小值；
（3）如图2，H，P分别为射线AC，AO上的动点，连接PH，PC是否存在这样的点P，使得△PCH为等腰三角形，△PHA为直角三角形同时成立．请直接写出满足条件的点P坐标．
【答案】解：（1）OB＝2OC＝4，则点B、C的坐标分别为：（0，﹣4）、（0，2），
将点C的坐标代入AC：y＝﹣x+b1并解得：
AC的表达式为：y＝﹣x+2，
令y＝0，则x＝6，故点A（6，0），
将点B、A的坐标代入y＝kx+b2得：，解得：，
故直线AB的表达式为：y＝x﹣4，即k＝；

（2）由点B、C的坐标得，BC＝6，
S△ACD＝S△BCD﹣S△BCA＝×BC×（xD﹣xA）＝×6（xD﹣6）＝9，
解得：xD＝9，
当x＝9时，y＝x﹣4＝2，故点D（9，2）；
CF＝FA，即CF＝AC＝＝，
过点F作FH⊥y轴于点H，

由直线AC的表达式知，∠OCA＝60°，
则HF＝CFsin60°＝＝，CH＝，故点F（，），
作点D关于x轴的对称点D′（9，﹣2），连接C′D′，当D′、C′、F三点共线时，MD+MC′最小，
MD+MC′最小值为D′F﹣F′C′＝D′F﹣CF＝﹣＝﹣；

（3）由直线AC的表达式知，∠CAO＝30°，AC＝＝4；
①∠PHA＝90°，当点H在线段AC上时，
则△PHC为等腰直角三角形，
设HP＝CH＝a，
则AP＝2HP，HA＝＝a，
AC＝CH+HA＝aa＝4，解得：a＝6﹣2，
AP＝2a＝12﹣4，则AP＝6﹣（12﹣4）＝4﹣6，
故点P（4﹣6，0）．
当点H在AC的延长线时时，可得∠CPA＝15°，此时OP＝﹣6﹣4，可得P（﹣6﹣4，0）．
②∠CPH＝90°，当点H在线段AC上时，
则CPH为等腰三角形，则HP＝CP，
设HP＝CP＝a，则在Rt△PHA中，HA＝2HP＝2a，
∵∠CPH＝90°，
∴HP∥OC，
则，即＝，解得：a＝，
PA＝＝a＝4，
故点P（2，0）．
当点H在AC的延长线上时，同理可得P（﹣6，0）．
综上，点P的坐标为：（2，0）或（4﹣6，0）或（﹣6﹣4，0）或（﹣6，0）．
16．如图1，将一个长方形纸片AOBC放置在平面直角坐标系中，点O、A、B的坐标分别为（0，0）、（0，6）和（8，0），若点D是线段AB上的一个动点．
（1）点C的坐标为　 　；
（2）如果存在这样的点D，使得△BCD为等腰三角形，求出所有符合条件AD的长；
（3）点M在线段BC上，点N在直线y＝2x﹣6第一象限的图象上，若△AMN是等腰直角三角形，且∠ANM＝90°，请直接写出点N的坐标．

【答案】解：（1）∵点A（0，6），故OA＝6，
∵点B（8，0），故OB＝8，
故点C（8，6），
故答案为：（8，6）；

（2）AB＝＝10，
①当BD＝BC时，
BD＝BC＝6，
则AD＝AB﹣BD＝10﹣6＝4；
②当BC＝CD时，如图1，

过点C作CH⊥AB于点H，
则S△ABC＝AB•CH＝AC•BC，即10×CH＝6×8，解得：CH＝4.8，
DH＝＝＝3.6，
∵CB＝CD，故DH＝HB＝BD，
BD＝2CH＝7.2，
则AD＝AB﹣BD＝2.8；
③当BD＝CD时，则CD是Rt△ABC的中线，
故AD＝CD＝BD＝5；
综上，AD＝4或5或2.8；

（3）①当点M不与B、C重合时，如图2，

过点N作GH∥x轴，交y轴于点G，交BC的延长线于点H，
设点N（m，2m﹣6），
∵∠GNA+∠MNH＝90°，∠GNA+∠GAH＝90°，
∴∠GNA＝∠HNM，AM＝AN，
∴Rt△NGA≌Rt△MHN（AAS），
∴AG＝NH，即2m﹣6﹣6＝8﹣m，解得：m＝，
故点N（，）；
②当点M与点C重合时，
同理可得：点N（4，2）；
③当点M与点B重合时，N不存在；
故点N的坐标为：（，）或（4，2）．
17．如图，在平面直角坐标系中，四边形OABC是矩形，点O（0，0），点A（3，0），点C（0，4）；D为AB边上的动点．
（Ⅰ）如图1，将△ABC对折，使得点B的对应点B落在对角线AC上，折痕为CD，求此刻点D的坐标：
（Ⅱ）如图2，将△ABC对折，使得点A的与点C重合，折痕交AB于点D，交AC于点E，求直线CD的解析式；
（Ⅲ）在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

【答案】解：（Ⅰ）设D（3，b），根据折叠的性质可得B′D＝BD＝4﹣b，
由勾股定理，得
AC＝＝＝5，
由三角形的面积，得S△ACD＝AD•BC＝AC•B′D，即×3b＝×5×（4﹣b）．
解得b＝，即D（3，）；

（Ⅱ）由折叠可知：CD＝AD，
设AD＝x，则CD＝x，BD＝8﹣x，
由题意得，（8﹣x）2+42＝x2，
解得x＝5，
此时AD＝5，
∴D（4，5），
设直线CD为y＝kx+8，
把D（4，5）代入得5＝4k+8，解得k＝﹣，
∴直线CD的解析式为y＝﹣x+8；

（Ⅲ）①当点P与点O重合时，△APC≌△CBA，此时P（0，0）；
②当点P在第一象限时，如图1，

由△APC≌△CBA得∠ACP＝∠CAB，
则点P在直线CD上．过P作PQ⊥AD于点Q，
在Rt△ADP中，
AD＝，PD＝BD＝4﹣＝，AP＝BC＝2
由AD×PQ＝DP×AP得：×PQ＝×2，
∴PQ＝，
xP＝2+＝，则y＝﹣x+4＝，
故点P（，），
（也可通过Rt△APQ勾股定理求AQ长得到点P的纵坐标）；

③当点P在第二象限时，如图2，

同理可求得：CQ＝，
∴OQ＝4﹣＝，
故点P（﹣，），
综合得，满足条件的点P有三个，为（0，0）或（，）或（﹣，）．