

高中数学北师大版 (2019)必修 第一册3 函数的单调性和最值第1课时导学案
展开第1课时 函数的单调性
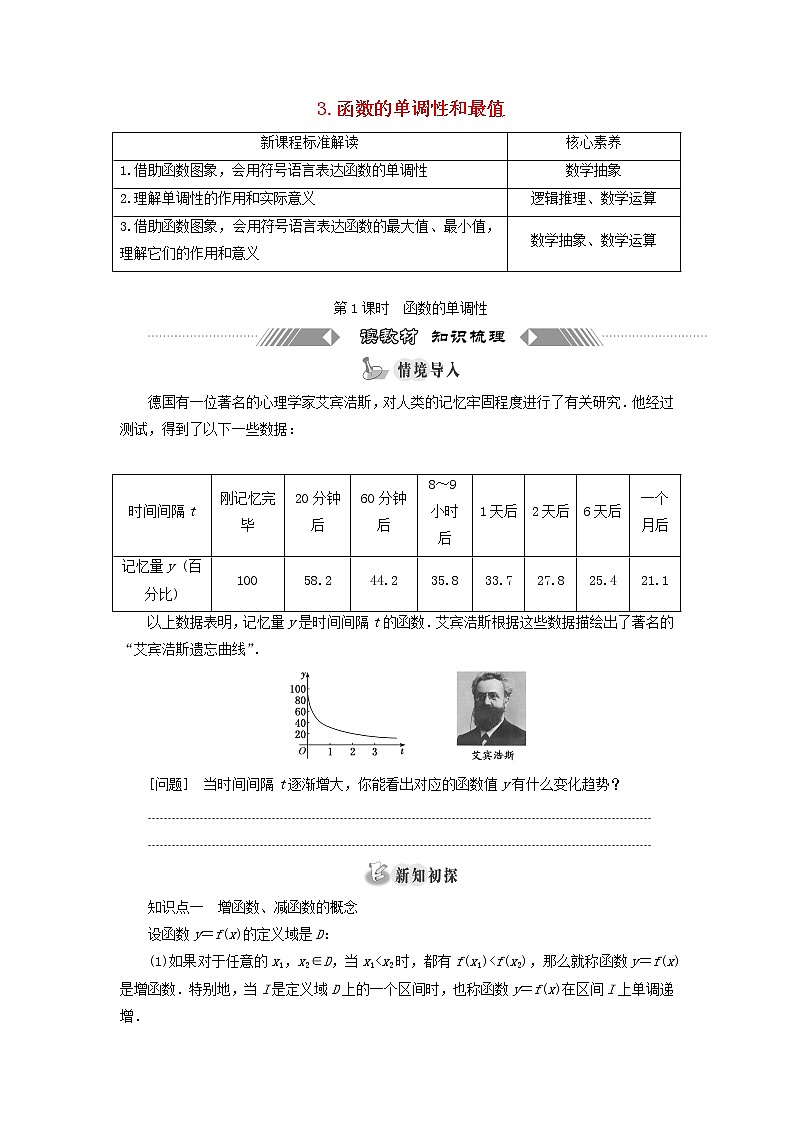
德国有一位著名的心理学家艾宾浩斯,对人类的记忆牢固程度进行了有关研究.他经过测试,得到了以下一些数据:
以上数据表明,记忆量y是时间间隔t的函数.艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯遗忘曲线”.
[问题] 当时间间隔t逐渐增大,你能看出对应的函数值y有什么变化趋势?
知识点一 增函数、减函数的概念
设函数y=f(x)的定义域是D:
(1)如果对于任意的x1,x2∈D,当x1
eq \a\vs4\al()
1.对区间D的要求
函数的单调性是函数在某个区间上的性质,这个区间可以是整个定义域,也可以是定义域的一部分.
2.x1,x2的三个特征
(1)同区间性,即x1,x2∈D;
(2)任意性,即不可用区间D上的两个特殊值代替x1,x2;
(3)有序性,即需要区分大小,通常规定x1
(1)单调递增:x1
下列函数f(x)中,满足对任意x1,x2∈(0,+∞),当x1
③f(x)=|x|;④f(x)=2x+1.
答案:②
知识点二 函数的单调性与单调区间
如果函数y=f(x)在区间I上单调递增或单调递减,那么就称函数y=f(x)在区间I上具有单调性,区间I为函数y=f(x)的单调区间.
eq \a\vs4\al()
1.函数在某个区间上是单调增(减)函数,但是在整个定义域上不一定是单调增(减)函数.如函数y=eq \f(1,x)(x≠0)在区间(-∞,0)和(0,+∞)上都是减函数,但是在整个定义域上不具有单调性.
2.一个函数出现两个或者两个以上的单调区间时,不能用“∪”连接,而应该用“和”或“,”连接.如函数y=eq \f(1,x)(x≠0)在区间(-∞,0)和(0,+∞)上都是减函数,不能认为y=eq \f(1,x)(x≠0)的单调减区间为(-∞,0)∪(0,+∞).
1.区间A一定是函数的定义域吗?
提示:不一定,可能是定义域的一部分.
2.函数y=eq \f(1,x)在定义域上是减函数吗?
提示:y=eq \f(1,x)在定义域上不是减函数,但是它有两个单调递减区间(-∞,0),(0,+∞).
1.下列函数中,在R上是增函数的是( )
A.y=|x| B.y=x
C.y=x2 D.y=eq \f(3,x)
解析:选B 根据题意,依次分析选项:对于A,y=|x|=eq \b\lc\{(\a\vs4\al\c1(x,x≥0,,-x,x<0,))在R上不是增函数,不符合题意;对于B,y=x是正比例函数,在R上是增函数,符合题意;对于C,y=x2是二次函数,在R上不是增函数,不符合题意;对于D,y=eq \f(3,x)是反比例函数,在R上不是增函数,不符合题意.
2.如图所示的是定义在区间[-5,5]上的函数y=f(x)的图象,则函数的单调递减区间是________,在区间________上是增函数.
解析:观察图象可知单调递增区间为[-5,-2],[1,3],单调递减区间为[-2,1],[3,5].
答案:[-2,1]和[3,5] [-5,-2]和[1,3]
3.若函数f(x)=ax-3在R上单调递增,则a的取值范围为________.
答案:(0,+∞)
[例1] 判断函数f(x)=eq \f(1,x2-1)在区间(1,+∞)上的单调性,并用单调性的定义证明.
[解] 函数f(x)=eq \f(1,x2-1)在区间(1,+∞)上是减函数.
证明如下:
任取x1,x2∈(1,+∞),且x1
=eq \f(xeq \\al(2,2)-xeq \\al(2,1),(xeq \\al(2,1)-1)(xeq \\al(2,2)-1))=eq \f((x2+x1)(x2-x1),(xeq \\al(2,1)-1)(xeq \\al(2,2)-1)).
∵x1
又x1,x2∈(1,+∞),
∴x2+x1>0,xeq \\al(2,1)-1>0,xeq \\al(2,2)-1>0.
∴eq \f((x2+x1)(x2-x1),(xeq \\al(2,1)-1)(xeq \\al(2,2)-1))>0,
即f(x1)>f(x2).
∴f(x)在区间(1,+∞)上单调递减.
eq \a\vs4\al()
利用定义证明函数单调性的步骤
[跟踪训练]
1.(多选)下列函数在(-∞,0)上为增函数的是( )
A.y=|x|+1 B.y=eq \f(|x|,x)
C.y=-eq \f(x2,|x|) D.y=x+eq \f(x,|x|)
解析:选CD y=|x|+1=-x+1(x<0)在(-∞,0)上为减函数;y=eq \f(|x|,x)=-1(x<0)在(-∞,0)上既不是增函数也不是减函数;y=-eq \f(x2,|x|)=x(x<0)在(-∞,0)上是增函数;y=x+eq \f(x,|x|)=x-1(x<0)在(-∞,0)上也是增函数,故选C、D.
2.利用单调性的定义,证明函数y=eq \f(x+2,x+1)在(-1,+∞)上是减函数.
证明:任取x1,x2∈(-1,+∞),且x1
因为-1
所以eq \f(x2-x1,(x1+1)(x2+1))>0,即f(x1)-f(x2)>0,f(x1)>f(x2).
所以y=eq \f(x+2,x+1)在(-1,+∞)上是减函数.
[例2] (链接教科书第63页B组2题)已知函数f(x)=x2-4|x|+3,x∈R.
(1)画出函数的图象;
(2)根据图象写出它的单调区间.
[解] (1)f(x)=x2-4|x|+3=eq \b\lc\{(\a\vs4\al\c1(x2-4x+3,x≥0,,x2+4x+3,x<0.))
图象如图所示:
(2)由图象可知函数f(x)的单调递增区间为(-2,0),(2,+∞),单调递减区间为(-∞,-2],[0,2].
eq \a\vs4\al()
求函数单调区间的2种方法
(1)定义法:即先求出定义域,再利用定义法进行判断求解;
(2)图象法:即先画出图象,根据图象求单调区间.
[跟踪训练]
求函数f(x)=eq \f(1,x-1)的单调减区间.
解:函数f(x)=eq \f(1,x-1)的定义域为(-∞,1)∪(1,+∞),
设x1,x2∈(-∞,1),且x1
因为x1
所以f(x1)-f(x2)>0,即f(x1)>f(x2).
所以函数f(x)在(-∞,1)上单调递减,同理函数f(x)在(1,+∞)上单调递减.
综上,函数f(x)的单调递减区间是(-∞,1),(1,+∞).
[例3] (1)若函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上是增函数,则实数a的取值范围是________;
(2)已知函数y=f(x)是(-∞,+∞)上的增函数,且f(2x-3)>f(5x-6),则实数x的取值范围为________.
[解析] (1)∵f(x)=-x2-2(a+1)x+3的开口向下,要使f(x)在(-∞,3]上是增函数,只需-(a+1)≥3,即a≤-4.∴实数a的取值范围为(-∞,-4].
(2)∵f(x)在(-∞,+∞)上是增函数,
且f(2x-3)>f(5x-6),
∴2x-3>5x-6,即x<1.
∴实数x的取值范围为(-∞,1).
[答案] (1)(-∞,-4] (2)(-∞,1)
[母题探究]
1.(变条件)若本例(1)的函数f(x)在(1,2)上是单调函数,求a的取值范围.
解:由题意可知-(a+1)≤1或-(a+1)≥2,即a≤-3或a≥-2.
所以a的取值范围为(-∞,-3]∪[-2,+∞).
2.(变条件)若本例(2)的函数f(x)是定义在(0,+∞)上的减函数,求x的范围.
解:由题意可知,eq \b\lc\{(\a\vs4\al\c1(2x-3>0,,5x-6>0,,2x-3<5x-6,))解得x>eq \f(3,2).
∴x的取值范围为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2),+∞)).
eq \a\vs4\al()
1.利用单调性比较大小或解不等式的方法
(1)利用函数的单调性可以比较函数值或自变量的大小.在解决比较函数值的问题时,要注意将对应的自变量转化到同一个单调区间上;
(2)在求解与抽象函数有关的不等式时,往往是利用函数的单调性将“f”符号脱掉,使其转化为具体的不等式求解.此时应特别注意函数的定义域.
2.已知函数的单调性求参数的取值范围的一般方法
(1)将参数看成已知数,求函数的单调区间,再与已知的单调区间比较,求出参数的取值范围;
(2)运用函数单调性的定义建立关于参数的不等式(组),解不等式(组)求出参数的取值范围.
[跟踪训练]
1.若函数f(x)在(-∞,-1]上是增函数,则下列关系式中成立的是( )
A.feq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(3,2)))
且-2<-eq \f(3,2)<-1,
∴f(-2)
解得eq \f(8,3)
复合函数y=f(g(x))的单调性
[典例] 已知函数f(x)=eq \f(2,x-1),x∈[2,6].
(1)试判断此函数在x∈[2,6]上的单调性;
(2)根据(1)的判断过程,归纳出解题步骤.
提示:(1)函数f(x)=eq \f(2,x-1)可分解为函数y=eq \f(2,u)和函数u=x-1.
因为x∈[2,6],所以u∈[1,5],显然函数u=x-1在x∈[2,6]上单调递增,函数y=eq \f(2,u)在u∈[1,5]上单调递减,由复合函数的单调性,知f(x)=eq \f(2,x-1)在x∈[2,6]上单调递减.
(2)解题步骤为:先求函数的定义域,接着分解复合函数,再判断每一层函数的单调性,最后根据复合函数的单调性确定函数的单调性.
[结论] 复合函数的单调性:一般地,对于复合函数y=f(g(x)),单调性如表所示,简记为“同增异减”.
[迁移应用]
求函数f(x)=eq \r(8-2x-x2)的单调区间.
解:由题意可知8-2x-x2≥0,解得-4≤x≤2,
∴函数f(x)的定义域为[-4,2].
设y=eq \r(u),u=8-2x-x2.
二次函数u=8-2x-x2=-(x+1)2+9的单调递增区间是(-∞,-1],单调递减区间是(-1,+∞).
∴函数y=f(x)的单调递增区间是[-4,-1],单调递减区间是(-1,2].
1.函数f(x)在R上是减函数,则有( )
A.f(3)
解析:选C 因为函数f(x)在R上是减函数,3<5,所以f(3)>f(5).
2.函数f(x)=-x2+2x+3的单调减区间是( )
A.(-∞,1) B.(1,+∞)
C.(-∞,2) D.(2,+∞)
解析:选B 易知函数f(x)=-x2+2x+3是图象开口向下的抛物线,其对称轴为x=1,所以其单调减区间是(1,+∞).
3.若函数y=ax与y=-eq \f(b,x)在(0,+∞)上都单调递增,则函数y=ax2+bx在(0,+∞)上( )
A.单调递增 B.单调递减
C.先增后减 D.先减后增
解析:选A 由于函数y=ax与y=-eq \f(b,x)在(0,+∞)上均单调递增,故a>0,b>0,故二次函数f(x)=ax2+bx的图象开口向上,且对称轴为直线x=-eq \f(b,2a)<0,故函数y=ax2+bx在(0,+∞)上单调递增.
4.(多选)如果函数f(x)在[a,b]上单调递增,则对于任意的x1,x2∈[a,b](x1≠x2),下列结论中正确的是( )
A.eq \f(f(x1)-f(x2),x1-x2)>0
B.(x1-x2)[f(x1)-f(x2)]>0
C.f(a)≤f(x1)
解析:选ABD 由函数单调性的定义可知,若函数y=f(x)在给定的区间上单调递增,则x1-x2与f(x1)-f(x2)同号,由此可知,选项A、B正确;对于C,若x1>x2,则f(x1)>f(x2),故C不正确;对于D,因为f(x)在区间[a,b]上单调,且x1≠x2,所以f(x1)≠f(x2),故D正确.
5.已知函数y=-x2+4ax在区间[-1,2]上单调递减,则实数a的取值范围是________.
解析:根据题意,知函数y=-x2+4ax为二次函数,且开口向下,其对称轴为x=2a,
若其在区间[-1,2]上单调递减,则2a≤-1,
所以a≤-eq \f(1,2),即a的取值范围为eq \b\lc\(\rc\](\a\vs4\al\c1(-∞,-\f(1,2))).
答案:eq \b\lc\(\rc\](\a\vs4\al\c1(-∞,-\f(1,2)))
新课程标准解读
核心素养
1.借助函数图象,会用符号语言表达函数的单调性
数学抽象
2.理解单调性的作用和实际意义
逻辑推理、数学运算
3.借助函数图象,会用符号语言表达函数的最大值、最小值,理解它们的作用和意义
数学抽象、数学运算
时间间隔t
刚记忆完毕
20分钟后
60分钟后
8~9小时后
1天后
2天后
6天后
一个月后
记忆量y (百分比)
100
58.2
44.2
35.8
33.7
27.8
25.4
21.1
利用定义判断或证明函数的单调性
求函数的单调区间
函数单调性的应用
g(x)
f(x)
f(g(x))
增
增
增
增
减
减
减
增
减
减
减
增
数学3.2 函数的基本性质第1课时导学案: 这是一份数学3.2 函数的基本性质第1课时导学案,共13页。
高中北师大版 (2019)第二章 函数3 函数的单调性和最值第2课时导学案: 这是一份高中北师大版 (2019)第二章 函数3 函数的单调性和最值第2课时导学案,共6页。
高中数学2.2 函数的表示法第2课时学案: 这是一份高中数学2.2 函数的表示法第2课时学案,共8页。













