人教版七年级下册5.1.2 垂线第2课时复习练习题

这是一份人教版七年级下册5.1.2 垂线第2课时复习练习题，共9页。试卷主要包含了已知在同一平面内，下列说法正确的有，图②等内容，欢迎下载使用。
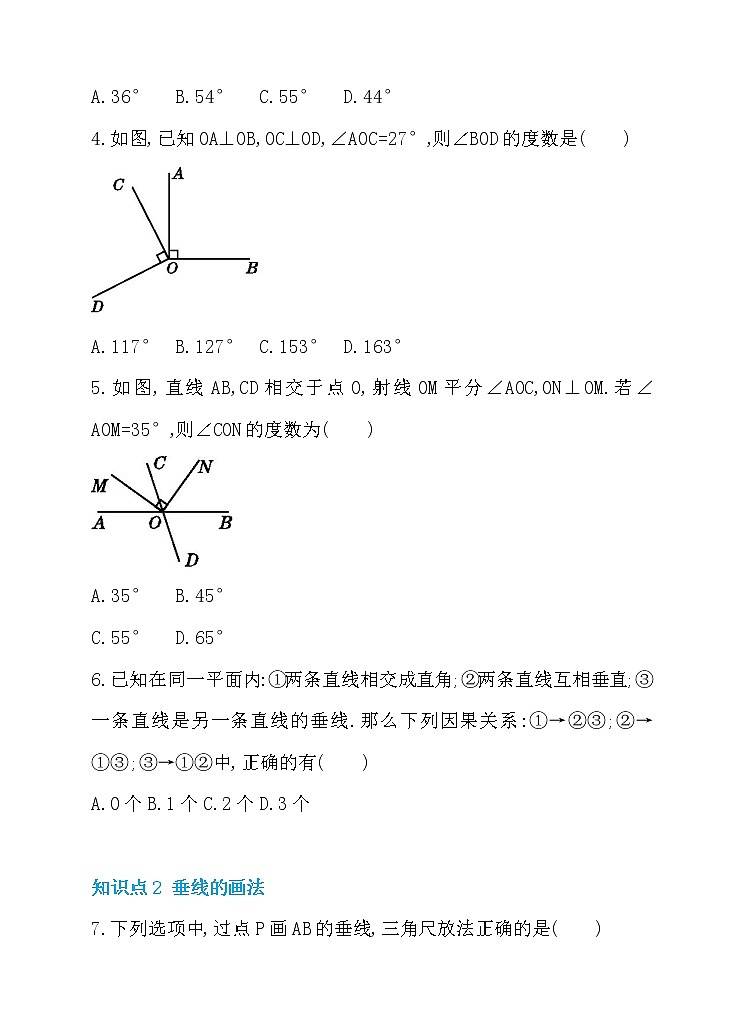
5.1 相交线第 2 课时 垂线基础训练知识1 点垂直的定义1.如图,OA⊥OB,∠1=35°,则∠2的度数是(　　)A.35° B.45° C.55° D.70°2.如图,CD⊥EF,垂足为O,AB是过点O的直线,∠1=50°,则∠2的度数为(　　)A.50° B.40° C.60° D.70°3.如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为(　　)A.36° B.54° C.55° D.44°4.如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD的度数是(　　)A.117° B.127° C.153° D.163°5.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON的度数为(　　)A.35° B.45°C.55° D.65°6.已知在同一平面内:①两条直线相交成直角;②两条直线互相垂直;③一条直线是另一条直线的垂线.那么下列因果关系:①→②③;②→①③;③→①②中,正确的有(　　)A.0个 B.1个 C.2个 D.3个 知识点2 垂线的画法7.下列选项中,过点P画AB的垂线,三角尺放法正确的是(　　)8.过一条线段外一点,作这条线段的垂线,垂足在(　　)A.这条线段上       B.这条线段的端点处C.这条线段的延长线上 D.以上都有可能知识点3 垂线的性质9.下列说法正确的有(　　)①在同一平面内,过直线上一点有且只有一条直线垂直于已知直线;②在同一平面内,过直线外一点有且只有一条直线垂直于已知直线;③在同一平面内,过一点可以画一条直线垂直于已知直线;④在同一平面内,有且只有一条直线垂直于已知直线.A.1个  B.2个 C.3个  D.4个10.如图,过点P作直线l的垂线和斜线,下列叙述正确的是(　　)A.都能作且只能作一条B.垂线能作且只能作一条,斜线可作无数条C.垂线能作两条,斜线可作无数条D.均可作无数条11.如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是(　　)A.过两点只有一条直线B.在同一平面内,过两点有且只有一条直线与已知直线垂直C.在同一平面内,过一点有且只有一条直线与已知直线垂直D.两点之间,线段最短易错点 误认为垂足一定要在线段或射线上而导致错误12.(1)在图①中,过AB外一点M作AB的垂线;(2)在图②中,过点A,B分别作OB,OA的垂线. 提升训练考查角度1 利用垂直的定义求角(分类讨论思想)13.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是多少?  考查角度2 利用垂直的定义、对顶角(或邻补角)的性质求角14.如图,直线AB与CD交于点O,OE⊥AB于点O,∠EOD：∠DOB=3：1,求∠COE的度数.   探究培优拔尖角度1 利用垂直的定义和周角求角15.已知OA⊥OB,OC⊥OD.(1)如图①,若∠BOC=50°,求∠AOD的度数;(2)如图②,若∠BOC=60°,求∠AOD的度数;(3)根据(1)(2)的结果猜想∠AOD与∠BOC有怎样的关系?并根据图①说明理由;(4)如图②,若∠BOC∶∠AOD=7∶29,求∠BOC和∠AOD的度数.    拔尖角度2 利用垂线的作法探究两角关系(验证法)16.(1)在图①中以P为顶点作∠P,使∠P的两边分别和∠1的两边垂直;(2)量一量∠P和∠1的度数,它们之间的数量关系是　　　　; (3)同样在图②和图③中以P为顶点作∠P,使∠P的两边分别和∠1的两边垂直,分别写出图②和③中∠P和∠1之间的数量关系(不要求写出理由).图②:　　　　,图③:　　　　; (4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角　　　　(不要求写出理由).  参考答案1.【答案】C2.【答案】B　解：因为CD⊥EF,所以∠DOF=90°,即∠1+∠DOB=90°,而∠1=50°,所以∠DOB=40°.又∠DOB与∠2是对顶角,所以∠2=∠DOB=40°,故选B.3.【答案】B　解：因为OC⊥OD,所以∠COD=90°,又因为∠AOC+∠COD+∠DOB=180°,所以∠DOB=180°-36°-90°=54°.故选B.4.【答案】C　 5.【答案】C　6.【答案】D　 7.【答案】C　8.【答案】D9.【答案】C　解：①②③的说法都正确,但④的说法是错误的,平面内有无数条直线垂直于已知直线,故选C.10.【答案】B　  11.【答案】C12.解:(1)如图①所示.(2)如图②所示.分析：本题易错之处在于误认为垂足一定落在线段或射线上.13.解:如图①,当OC,OD在直线AB的同侧时,因为OC⊥OD,所以∠COD=90°.因为∠AOC=30°,所以∠BOD=180°-∠COD-∠AOC=60°.如图②,当OC,OD在直线AB的异侧时,因为OC⊥OD,所以∠COD=90°.因为∠AOC=30°,所以∠AOD=90°-∠AOC=60°.所以∠BOD=180°-∠AOD=120°.解：射线OC,OD的位置有两种情况:位于直线AB的同侧和位于直线AB的异侧,易错之处在于考虑不周忽略其中一种情况.14.解:因为OE⊥AB,所以∠EOB=∠EOA=90°.因为∠EOD∶∠DOB=3∶1,所以∠DOB=90°×=22.5°.所以∠AOC=∠DOB=22.5°,所以∠COE=∠EOA+∠AOC=90°+22.5°=112.5°.15.解:(1)因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB-∠BOC=90°-50°=40°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=40°+90°=130°.(2)因为OA⊥OB,所以∠AOB=90°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=360°-∠AOB-∠BOC-∠COD=360°-90°-60°-90°=120°.(3)∠AOD与∠BOC互补.理由如下:因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB-∠BOC=90°-∠BOC.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=90°-∠BOC+90°=180°-∠BOC,所以∠AOD+∠BOC=180°,即∠AOD与∠BOC互补.(4)由(3)知∠BOC+∠AOD=180°,又因为∠BOC∶∠AOD=7∶29,所以∠BOC=×180°=35°,∠AOD=×180°=145°.16.解:(1)如图①所示.(2)∠1+∠P=180°(3)如图②③,∠1=∠P;∠1=∠APC或∠1+∠BPC=180°(4)相等或互补