初中数学北师大版七年级下册7 整式的除法课时训练

这是一份初中数学北师大版七年级下册7 整式的除法课时训练，共5页。试卷主要包含了计算，观察下列各式，观察下列式等内容，欢迎下载使用。

A．±48B．±24C．48D．24
2．计算：（8x5﹣6x3﹣4x2）÷（﹣2x）＝（ ）
A．﹣4x4﹣3x2+2xB．﹣4x4+3x2+2x
C．4x4+3x2﹣2xD．4x4﹣3x2﹣2x
3．观察下列各式：
（x2﹣1）÷（x﹣1）＝x+1．
（x3﹣1）÷（x﹣1）＝x2+x+1，
（x4﹣1）÷（x﹣1）＝x3+x2+x+1，
（x5﹣1）÷（x﹣1）＝x4+x3+x2+x+1，
根据上述规律计算2+22+23+…+262+263的值为（ ）
A．264﹣1B．264﹣2C．264+1D．264+2
4．若多项式A除以2x2﹣3，得到的商式为3x﹣4，余式为5x+2，则A＝ ．
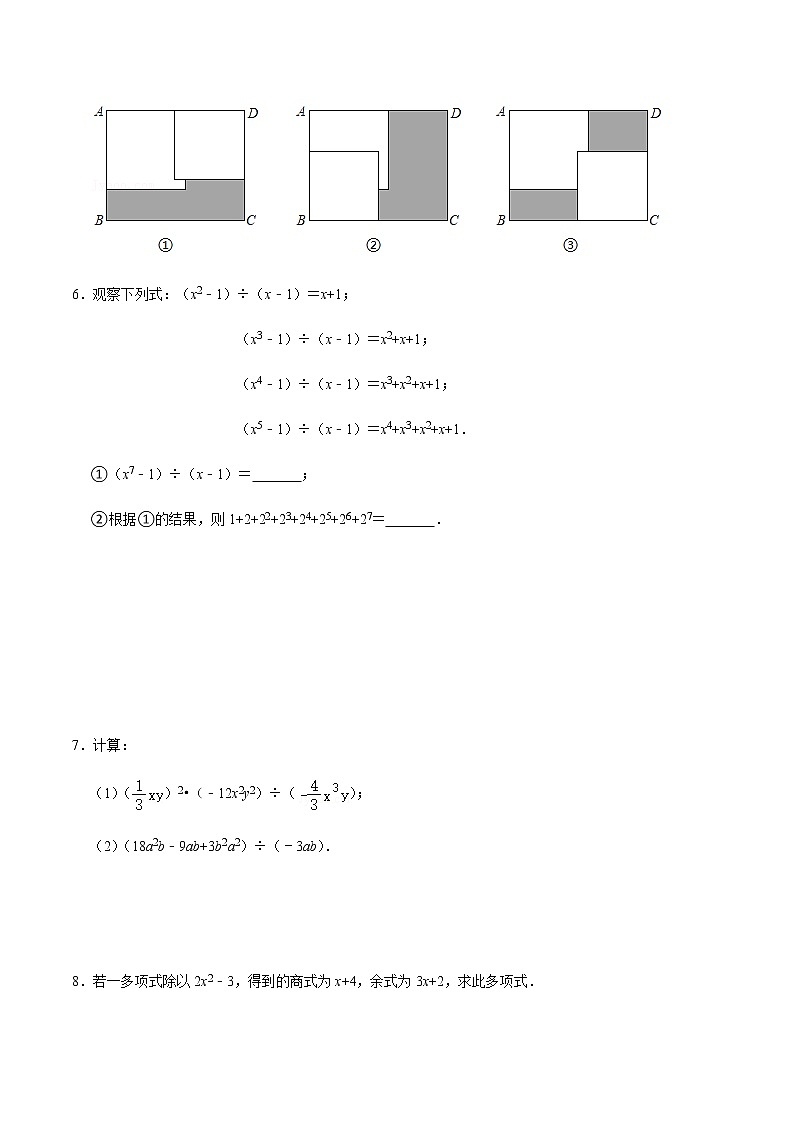
5．长方形ABCD内放入两张边长分别为acm和bcm（a＞b）的小正方形纸片．按照图①放置，矩形纸片没有被两个正方形覆盖的部分（阴影部分）的面积为；按照图②放置，矩形纸片没有被两个正方形覆盖的部分的面积为；按图③放置，矩形纸片没有被两个正方形覆盖的部分的面积为，已知AD﹣AB＝1，3a﹣2b＝6，S1﹣S3＝a﹣b，S2﹣S3＝4a﹣2b，则b的值为 ．
6．观察下列式：（x2﹣1）÷（x﹣1）＝x+1；
（x3﹣1）÷（x﹣1）＝x2+x+1；
（x4﹣1）÷（x﹣1）＝x3+x2+x+1；
（x5﹣1）÷（x﹣1）＝x4+x3+x2+x+1．
①（x7﹣1）÷（x﹣1）＝ ；
②根据①的结果，则1+2+22+23+24+25+26+27＝ ．
7．计算：
（1）（）2•（﹣12x2y2）÷（）；
（2）（18a2b﹣9ab+3b2a2）÷（﹣3ab）．
8．若一多项式除以2x2﹣3，得到的商式为x+4，余式为3x+2，求此多项式．
9．观察下列各式：
（x﹣1）÷（x﹣1）＝1；
（x2﹣1）÷（x﹣1）＝x+1；
（x3﹣1）÷（x﹣1）＝x2+x+1；
（x4﹣1）÷（x﹣1）＝x3+x2+x+1．
根据上面各式的规律可得（ ）÷（x﹣1）＝xn+xn﹣1+…+x+1；利用规律完成下列问题：
（1）52021+52020+52019+…+51+1＝ ；
（2）求（﹣3）20+（﹣3）19+（﹣3）18+…+（﹣3）的值．
10．我们已经学习过多项式除以单项式，多项式除以多项式一般可用竖式计算，步骤如下：
①把被除式、除式按某个字母作降幂排列，并把所缺的项用零补齐；
②用被除式的第一项除以除式第一项，得到商式的第一项；
③用商式的第一项去乘除式，把积写在被除式下面（同类项对齐），消去相等项；
④把减得的差当作新的被除式，再按照上面的方法继续演算，直到余式为零或余式的次数低于除式的次数时为止，被除式＝除式×商式+余式，若余式为零，说明这个多项式能被另一个多项式整除．
例如：计算（6x4﹣7x3﹣x2﹣1）÷（2x+1），可用竖式除法如图：
所以6x4﹣7x3﹣x2﹣1除以2x+1，商式为3x3﹣5x2+2x﹣1，余式为0．
根据阅读材料，请回答下列问题：
（1）（x3﹣4x2+7x﹣5）÷（x﹣2）的商是 ，余式是 ；
（2）x3﹣x2+ax+b能被x2+2x+2整除，求a，b的值．