专题17等腰三角形与直角三角形（共42题）-2021年中考数学真题分项汇编（原卷版+解析版）【全国通用】

这是一份专题17等腰三角形与直角三角形（共42题）-2021年中考数学真题分项汇编（原卷版+解析版）【全国通用】，文件包含专题17等腰三角形与直角三角形共42题-2021年中考数学真题分项汇编解析版全国通用第01期docx、专题17等腰三角形与直角三角形共42题-2021年中考数学真题分项汇编原卷版全国通用第01期docx等2份试卷配套教学资源，其中试卷共88页， 欢迎下载使用。
2021年中考数学真题分项汇编【全国通用】（第01期）
专题17等腰三角形与直角三角形（共42题）
姓名：__________________ 班级：______________ 得分：_________________
一、单选题
1．（2021·湖南衡阳市·中考真题）下列命题是真命题的是（ ）．
A．正六边形的外角和大于正五边形的外角和 B．正六边形的每一个内角为
C．有一个角是的三角形是等边三角形 D．对角线相等的四边形是矩形
【答案】B
【分析】
根据多边形外角和、正多边形内角和、等边三角形、矩形的性质，对各个选项逐个分析，即可得到答案．
【详解】
正六边形的外角和，和正五边形的外角和相等，均为
∴选项A不符合题意；
正六边形的内角和为：
∴每一个内角为，即选项B正确；
三个角均为的三角形是等边三角形
∴选项C不符合题意；
对角线相等的平行四边形是矩形
∴选项D不正确；
故选：B．
【点睛】
本题考查了多边形外角和、正多边形内角和、等边三角形、矩形的知识；解题的关键是熟练掌握多边形外角和、正多边形内角和、等边三角形、矩形的性质，从而完成求解．
2．（2021·江苏扬州市·中考真题）如图，在的正方形网格中有两个格点A、B，连接，在网格中再找一个格点C，使得是等腰直角三角形，满足条件的格点C的个数是（ ）

A．2 B．3 C．4 D．5
【答案】B
【分析】
根据题意，结合图形，分两种情况讨论：①AB为等腰直角△ABC底边；②AB为等腰直角△ABC其中的一条腰．
【详解】
解：如图：分情况讨论：
①AB为等腰直角△ABC底边时，符合条件的C点有0个；
②AB为等腰直角△ABC其中的一条腰时，符合条件的C点有3个．
故共有3个点，
故选：B．

【点睛】
本题考查了等腰三角形的判定；解答本题关键是根据题意，画出符合实际条件的图形，数形结合的思想是数学解题中很重要的解题思想．
3．（2021·浙江宁波市·中考真题）如图，在中，于点D，．若E，F分别为，的中点，则的长为（ ）

A． B． C．1 D．
【答案】C
【分析】
根据条件可知△ABD为等腰直角三角形，则BD=AD，△ADC是30°、60°的直角三角形，可求出AC长，再根据中位线定理可知EF=。
【详解】
解：因为AD垂直BC，
则△ABD和△ACD都是直角三角形，
又因为
所以AD=，
因为sin∠C=，
所以AC=2，
因为EF为△ABC的中位线，
所以EF==1，
故选：C．
【点睛】
本题主要考查了等腰直角三角形、锐角三角形函数值、中位线相关知识，根据条件分析利用定理推导，是解决问题的关键．
4．（2021·四川凉山彝族自治州·中考真题）下列命题中，假命题是（ ）
A．直角三角形斜边上的中线等于斜边的一半
B．等腰三角形顶角的平分线，底边上的中线，底边上的高相互重合
C．若，则点B是线段AC的中点
D．三角形三条边的垂直平分线的交点叫做这个三角形的外心
【答案】C
【分析】
根据中点的定义，直角三角形的性质，三线合一以及外心的定义分别判断即可．
【详解】
解：A、直角三角形斜边上的中线等于斜边的一半，故为真命题；
B、等腰三角形顶角的平分线，底边上的中线，底边上的高相互重合，故为真命题；
C、若在同一条直线上AB=BC，则点B是线段AC的中点，故为假命题；
D、三角形三条边的垂直平分线的交点叫做这个三角形的外心，故为真命题；
故选C．
【点睛】
本题考查了中点的定义，直角三角形的性质，三线合一以及外心的性质，属于基础知识，要熟练掌握．
5．（2021·四川泸州市·中考真题）在锐角ABC中，∠A，∠B，∠C所对的边分别为a，b，c，有以下结论：（其中R为ABC的外接圆半径）成立．在ABC中，若∠A=75°，∠B=45°，c=4，则ABC的外接圆面积为（ ）
A． B． C． D．
【答案】A
【分析】
方法一：先求出∠C，根据题目所给的定理， , 利用圆的面积公式S圆=．
方法二：设△ABC的外心为O，连结OA，OB，过O作OD⊥AB于D，由三角形内角和可求∠C=60°，由圆周角定理可求∠AOB=2∠C=120°，由等腰三角形性质，∠OAB=∠OBA=，由垂径定理可求AD=BD=，利用三角函数可求OA=，利用圆的面积公式S圆=．
【详解】
解:方法一：∵∠A=75°，∠B=45°，
∴∠C=180°-∠A-∠B=180°-75°-45°=60°，
有题意可知，
∴，
∴S圆=．
方法二：设△ABC的外心为O，连结OA，OB，过O作OD⊥AB于D，
∵∠A=75°，∠B=45°，
∴∠C=180°-∠A-∠B=180°-75°-45°=60°，
∴∠AOB=2∠C=2×60°=120°，
∵OA=OB，
∴∠OAB=∠OBA=，
∵OD⊥AB，AB为弦，
∴AD=BD=，
∴AD=OAcos30°，
∴OA=，
∴S圆=．
故答案为A．

【点睛】
本题考查三角形的外接圆，三角形内角和，圆周角定理，等腰三角形性质，垂径定理，锐角三角函数，圆的面积公式，掌握三角形的外接圆，三角形内角和，圆周角定理，等腰三角形性质，垂径定理，锐角三角函数，圆的面积公式是解题关键．
6．（2021·浙江温州市·中考真题）图1是第七届国际数学教育大会（ICME）的会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形．若．，则的值为（ ）

A． B． C． D．
【答案】A
【分析】
根据勾股定理和三角函数求解．
【详解】
∵在中，，
∴
在中，，
故选：A．
【点睛】
本题主要考查勾股定理和三角函数．如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么．
7．（2021·四川凉山彝族自治州·中考真题）如图，中，，将沿DE翻折，使点A与点B重合，则CE的长为（ ）

A． B．2 C． D．
【答案】D
【分析】
先在RtABC中利用勾股定理计算出AB=10，再利用折叠的性质得到AE=BE，AD=BD=5，设AE=x，则CE=AC-AE=8-x，BE=x，在Rt△BCE中根据勾股定理可得到x2=62+（8-x）2，解得x，可得CE．
【详解】
解：∵∠ACB=90°，AC=8，BC=6，
∴AB==10，
∵△ADE沿DE翻折，使点A与点B重合，
∴AE=BE，AD=BD=AB=5，
设AE=x，则CE=AC-AE=8-x，BE=x，
在Rt△BCE中
∵BE2=BC2+CE2，
∴x2=62+（8-x）2，解得x=，
∴CE==，
故选：D．
【点睛】
本题考查了折叠的性质：折叠前后两图象全等，即对应角相等，对应边相等．也考查了勾股定理．
8．（2021·陕西中考真题）如图，在菱形中，，连接、，则的值为（ ）

A． B． C． D．
【答案】D
【分析】
设AC与BD的交点为O，由题意易得，，进而可得△ABC是等边三角形，，然后问题可求解．
【详解】
解：设AC与BD的交点为O，如图所示：

∵四边形是菱形，
∴，，
∵，
∴△ABC是等边三角形，
∴，
∴，
∴，
∴，
∴；
故选D．
【点睛】
本题主要考查菱形的性质、含30°角的直角三角形的性质及勾股定理，熟练掌握菱形的性质、含30°角的直角三角形的性质及勾股定理是解题的关键．
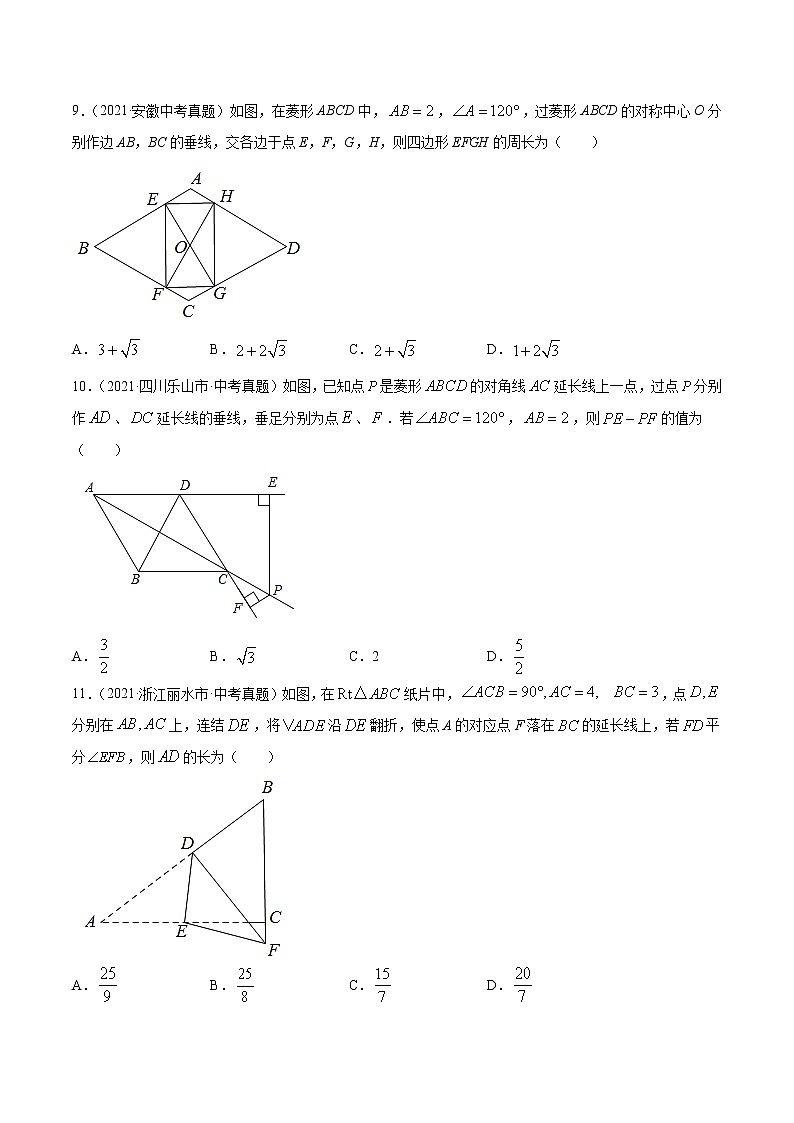
9．（2021·安徽中考真题）如图，在菱形ABCD中，，，过菱形ABCD的对称中心O分别作边AB，BC的垂线，交各边于点E，F，G，H，则四边形EFGH的周长为（ ）

A． B． C． D．
【答案】A
【分析】
依次求出OE=OF=OG=OH，利用勾股定理得出EF和OE的长，即可求出该四边形的周长．
【详解】
∵HF⊥BC,EG⊥AB,
∴∠BEO=∠BFO=90°，
∵∠A=120°，
∴∠B=60°，
∴∠EOF=120°，∠EOH=60°，
由菱形的对边平行，得HF⊥AD,EG⊥CD，
因为O点是菱形ABCD的对称中心，
∴O点到各边的距离相等，即OE=OF=OG=OH，
∴∠OEF=∠OFE=30°，∠OEH=∠OHE=60°，
∴∠HEF=∠EFG=∠FGH=∠EHG=90°，
所以四边形EFGH是矩形；
设OE=OF=OG=OH=x，
∴EG=HF=2x，，
如图，连接AC，则AC经过点O，
可得三角形ABC是等边三角形，
∴∠BAC=60°，AC=AB=2,
∴OA=1,∠AOE=30°，
∴AE=，
∴x=OE=
∴四边形EFGH的周长为EF+FG+GH+HE=,
故选A．

【点睛】
本题考查了菱形的性质、矩形的判定与性质、等边三角形的判定与性质、勾股定理、直角三角形的性质等内容，要求学生在理解相关概念的基础上学会应用，能分析并综合运用相关条件完成线段关系的转换，考查了学生的综合分析与应用的能力．
10．（2021·四川乐山市·中考真题）如图，已知点是菱形的对角线延长线上一点，过点分别作、延长线的垂线，垂足分别为点、．若，，则的值为（ ）

A． B． C．2 D．
【答案】B
【分析】
根据菱形的基性质，得到∠PAE=30°，,利用勾股理求出AC=，则AP= +PC，PE=AP=+PC ，由∠PCF=∠DCA=30°，得到PF=PC ，最后算出结果．
【详解】
解：∵四边形ABCD是菱形且∠ABC=120°，AB=2，
∴AB=BC=CD=DA=2，∠BAD=60°，AC⊥BD，
∴∠CAE=30︒，
∵AC⊥BD，∠CAE=30°，AD=2，
∴AC=，
∴AP=+PC，
在直角△AEP中，
∵∠PAE=30°，AP=+PC，
∴PE=AP=+PC，
在直角△PFC中，
∵∠PCF=30°，
∴PF=PC，
∴=+PC-PC=，
故选：B．
【点睛】
本题主要考查了菱形的基本性质、勾股定理的应用以及在直角三角形中，30°角所对的直角边等于斜边的一半，关键会在直角三角形中应用30°．
11．（2021·浙江丽水市·中考真题）如图，在纸片中，，点分别在上，连结，将沿翻折，使点A的对应点F落在的延长线上，若平分，则的长为（ ）

A． B． C． D．
【答案】D
【分析】
先根据勾股定理求出AB，再根据折叠性质得出∠DAE=∠DFE，AD=DF，然后根据角平分线的定义证得∠BFD=∠DFE=∠DAE，进而证得∠BDF=90°，证明Rt△ABC∽Rt△FBD，可求得AD的长．
【详解】
解：∵，
∴=5，
由折叠性质得：∠DAE=∠DFE，AD=DF，则BD=5﹣AD，
∵平分，
∴∠BFD=∠DFE=∠DAE，
∵∠DAE+∠B=90°，
∴∠BDF+∠B=90°，即∠BDF=90°，
∴Rt△ABC∽Rt△FBD，
∴即，
解得：AD=，
故选：D．
【点睛】
本题考查折叠性质、角平分线的定义、勾股定理、相似三角形的判定与性质、三角形的内角和定理，熟练掌握折叠性质和相似三角形的判定与性质是解答的关键．
12．（2021·四川自贡市·中考真题）如图，，，以点A为圆心，AC长为半径画弧，交y轴正半轴于点B，则点B的坐标为（ ）


A． B． C． D．
【答案】D
【分析】
先根据题意得出OA=8，OC=2，再根据勾股定理计算即可
【详解】
解：由题意可知：AC=AB
∵，
∴OA=8，OC=2
∴AC=AB=10
在Rt△OAB中，
∴B(0，6)
故选：D
【点睛】
本题考查勾股定理、正确写出点的坐标，圆的半径相等、熟练进行勾股定理的计算是关键
13．（2021·云南中考真题）在中，，若，则的长是（ ）
A． B． C．60 D．80
【答案】D
【分析】
根据三角函数的定义得到BC和AC的比值，求出BC，然后利用勾股定理即可求解．
【详解】
解：∵∠ABC=90°，sin∠A==，AC=100，
∴BC=100×3÷5=60，
∴AB==80，
故选D．
【点睛】
本题主要考查的是解直角三角形，掌握勾股定理和正弦函数的定义是解题的关键．
14．（2021·浙江金华市·中考真题）如图，在中，，以该三角形的三条边为边向形外作正方形，正方形的顶点都在同一个圆上．记该圆面积为，面积为，则的值是（ ）

A． B． C． D．
【答案】C
【分析】
先确定圆的圆心在直角三角形斜边的中点，然后利用全等三角形的判定和性质确定△ABC是等腰直角三角形，再根据直角三角形斜边中线的性质得到，再由勾股定理解得，解得，据此解题即可．
【详解】
解：如图所示，正方形的顶点都在同一个圆上，
圆心在线段的中垂线的交点上，即在斜边的中点，且AC=MC，BC=CG，
∴AG=AC+CG=AC+BC，BM=BC+CM=BC+AC，
∴AG=BM，
又∵OG=OM，OA=OB，
∴△AOG≌△BOM，
∴∠CAB=∠CBA，
∵∠ACB=90°，
∴∠CAB=∠CBA=45°，
，


，
．

故选：C．
【点睛】
本题考查勾股定理、直角三角形斜边的中线的性质、圆的面积、三角形的面积等知识，是重要考点，难度一般，掌握相关知识是解题关键．
15．（2021·浙江温州市·中考真题）由四个全等的直角三角形和一个小正方形组成的大正方形如图所示．过点作的垂线交小正方形对角线的延长线于点，连结，延长交于点．若，则的值为（ ）

A． B． C． D．
【答案】C
【分析】
如图，设BH交CF于P，CG交DF于Q，根据题意可知BE=PC=DF，AE=BP=CF，根据可得BE=PE=PC=PF=DF，根据正方形的性质可证明△FDG是等腰直角三角形，可得DG=FD，根据三角形中位线的性质可得PH=FQ，CH=QH=CQ，利用ASA可证明△CPH≌△GDQ，可得PH=QD，即可得出PH=BE，可得BH=，利用勾股定理可用BE表示长CH的长，即可表示出CG的长，进而可得答案．
【详解】
如图，设BH交CF于P，CG交DF于Q，
∵由四个全等的直角三角形和一个小正方形组成的大正方形，
∴BE=PC=DF，AE=BP=CF，
∵，
∴BE=PE=PC=PF=DF，
∵∠CFD=∠BPC，
∴DF//EH，
∴PH为△CFQ的中位线，
∴PH=QF，CH=HQ，
∵四边形EPFN是正方形，
∴∠EFN=45°，
∵GD⊥DF，
∴△FDG是等腰直角三角形，
∴DG=FD=PC，
∵∠GDQ=∠CPH=90°，
∴DG//CF，
∴∠DGQ=∠PCH，
在△DGQ和△PCH中，，
∴△DGQ≌△PCH，
∴PH=DQ，CH=GQ，
∴PH=DF=BE，CG=3CH，
∴BH=BE+PE+PH=，
在Rt△PCH中，CH==，
∴CG=BE，
∴．

故选：C．
【点睛】
本题考查正方形的性质、全等三角形的判定与性质、三角形中位线的性质及勾股定理，熟练掌握相关性质及判定定理是解题关键．
16．（2021·四川南充市·中考真题）如图，在矩形ABCD中，，，把边AB沿对角线BD平移，点，分别对应点A，B．给出下列结论：①顺次连接点，，C，D的图形是平行四边形；②点C到它关于直线的对称点的距离为48；③的最大值为15；④的最小值为．其中正确结论的个数是（ ）

A．1个 B．2个 C．3个 D．4个
【答案】D
【分析】
根据平移的性质和平行四边形的判定方法判断①，再利用等积法得出点C到BD的距离，从而对②做出判断，再根据三角形的三边关系判断③，如图，作关于的对称点，交于 连接，过作于 分别交于 证明 是最小值时的位置，再利用勾股定理求解，对④做出判断．
【详解】
解：由平移的性质可得AB//
且AB=
∵四边形ABCD为矩形
∴AB//CD，AB=CD=15
∴//CD且=CD
∴四边形CD为平行四边形，故①正确
在矩形ABCD中，BD===25
过A作AM⊥BD，CN⊥BD，则AM=CN

∴S△ABD=AB·CD= BD·AM
∴AM=CN==12
∴点C到的距离为24
∴点C到它关于直线的对称点的距离为48
∴故②正确
∵
∴当在一条直线时最大，
此时与D重合
∴的最大值==15
∴故③正确，
如图，作关于的对称点，交于 连接，过作于 分别交于
则 为的中位线， ，


由可得，

此时最小，
由②同理可得：

设 则
由勾股定理可得：

整理得：

解得：（负根舍去），


∴故④正确
故选D．
【点睛】
本题主要考查了平行四边形的判定，矩形的性质以及平移的性质,锐角三角函数的应用等知识点，熟练掌握相关的知识是解题的关键．
17．（2021·四川广元市·中考真题）如图，在中，，，点D是边的中点，点P是边上一个动点，连接，以为边在的下方作等边三角形，连接．则的最小值是（ ）

A． B．1 C． D．
【答案】B
【分析】
以CD为边作等边三角形CDE，连接EQ，由题意易得∠PDC=∠QDE，PD=QD，进而可得△PCD≌△QED，则有∠PCD=∠QED=90°，然后可得点Q是在QE所在直线上运动，所以CQ的最小值为CQ⊥QE时，最后问题可求解．
【详解】
解：以CD为边作等边三角形CDE，连接EQ，如图所示：

∵是等边三角形，
∴，
∵∠CDQ是公共角，
∴∠PDC=∠QDE，
∴△PCD≌△QED（SAS），
∵，，点D是边的中点，
∴∠PCD=∠QED=90°，，
∴点Q是在QE所在直线上运动，
∴当CQ⊥QE时，CQ取的最小值，
∴，
∴；
故选B．
【点睛】
本题主要考查等边三角形的性质、含30°直角三角形的性质及最短路径问题，熟练掌握等边三角形的性质、含30°直角三角形的性质及最短路径问题是解题的关键．
18．（2021·浙江绍兴市·中考真题）如图，菱形ABCD中，，点P从点B出发，沿折线方向移动，移动到点D停止．在形状的变化过程中，依次出现的特殊三角形是（ ）


A．直角三角形→等边三角形→等腰三角形→直角三角形
B．直角三角形→等腰三角形→直角三角形→等边三角形
C．直角三角形→等边三角形→直角三角形→等腰三角形
D．等腰三角形→等边三角形→直角三角形→等腰三角形
【答案】C
【分析】
是特殊三角形，取决于点P的某些特殊位置，按其移动方向，逐一判断即可．
【详解】
解：连接AC，BD，如图所示．
∵四边形ABCD是菱形，
∴AB=BC=CD=DA，∠D=∠B．
∵∠B=60°，
∴∠D=∠B=60°．
∴和都是等边三角形．
点P在移动过程中，依次共有四个特殊位置：

（1）当点P移动到BC边的中点时，记作．
∵是等边三角形，是 BC的中点，
∴．
∴．
∴是直角三角形．
（2）当点P与点C重合时，记作．
此时，是等边三角形；
（3）当点P移动到CD边的中点时，记为．
∵和都是等边三角形，
∴．
∴是直角三角形．
（4）当点P与点D重合时，记作．
∵，
∴是等腰三角形．
综上，形状的变化过程中，依次出现的特殊三角形是：
直角三角形→等边三角形→直角三角形→等腰三角形．
故选：C
【点睛】
本题考查了菱形的性质、直角三角形的判定、等腰三角形的判定、等边三角形的性质与判定等知识点，熟知特殊三角形的判定方法是解题的关键．
二、填空题
19．（2021·浙江绍兴市·中考真题）如图，在中，，，以点C为圆心，CA长为半径作弧，交直线BC于点P，连结AP，则的度数是_______．


【答案】或
【分析】
分①点P在BC的延长线上，②点P在CB的延长线上两种情况，再利用等腰三角形的性质即可得出答案．
【详解】
解：①当点P在BC的延长线上时，如图


∵，，
∴
∴
∵以点C为圆心，CA长为半径作弧，交直线BC于点P，
∴AC=PC
∴
∵
∴
∴
②当点P在CB的延长线上时，如图


由①得，
∵AC=PC
∴
∴
故答案为：或
【点睛】
本题主要考查了等腰三角形的性质，分类讨论不重不漏是解题的关键．
20．（2021·四川广安市·中考真题）如图，将三角形纸片折叠，使点、都与点重合，折痕分别为、.已知，，，则的长为_______．

【答案】
【分析】
由折叠的性质得出BE=AE，AF=FC，∠FAC=∠C=15°，得出∠AFE=30°，由等腰三角形的性质得出∠EAF=∠AFE=30°，证出△ABE是等边三角形，得出∠BAE=60°，求出AE=BE=2，证出∠BAF=90°，利用勾股定理求出AF，即CF，可得BC．
【详解】
解：∵把三角形纸片折叠，使点B、点C都与点A重合，折痕分别为DE，FG，
∴BE=AE，AF=FC，∠FAC=∠C=15°，
∴∠AFE=30°，又AE=EF，
∴∠EAF=∠AFE=30°，
∴∠AEB=60°，
∴△ABE是等边三角形，∠AED=∠BED=30°，
∴∠BAE=60°，
∵DE=，
∴AE=BE=AB==2，
∴BF=BE+EF=4，∠BAF=60°+30°=90°，
∴FC=AF==，
∴BC=BF+FC=，
故答案为：．
【点睛】
此题考查了翻折变换的性质、等腰三角形的性质、等边三角形的判定与性质、直角三角形的性质；根据折叠的性质得出相等的边和角是解题关键．
21．（2021·江苏苏州市·中考真题）如图．在中，，．若，则______．

【答案】54°
【分析】
首先根据等腰三角形的性质得出∠A=∠AEF，再根据三角形的外角和定理得出∠A+∠AEF=∠CFE，求出∠A的度数，最后根据三角形的内角和定理求出∠B的度数即可．
【详解】
∵ AF=EF，
∴ ∠A=∠AEF，
∵∠A+∠AEF=∠CFE=72°，
∴ ∠A=36°，
∵ ∠C=90°，∠A+∠B+∠C=180°，
∴ ∠B=180°-∠A-∠C=54°．
故答案为：54°．
【点睛】
本题考查了三角形的外角和定理，等腰三角形的性质，掌握相关定理和性质是解题的关键．
22．（2021·浙江中考真题）为庆祝中国共产党建党100周年，某校用红色灯带制作了一个如图所示的正五角星（是正五边形的五个顶点），则图中的度数是_______度．

【答案】36
【分析】
根据题意，得五边形（是正五边形的五个顶点）为正五边形，且；根据多边形内角和性质，得正五边形内角和，从而得；再根据补角、等腰三角形、三角形内角和性质计算，即可得到答案．
【详解】
∵正五角星（是正五边形的五个顶点）
∴五边形（是正五边形的五个顶点）为正五边形，且

∴正五边形内角和为：
∴
∴
∵
∴
∴
故答案为：36．
【点睛】
本题考查了正多边形、多边形内角和、补角、等腰三角形、三角形内角和的知识；解题的关键是熟练掌握正多边形、多边形内角和、等腰三角形、三角形内角和的性质，从而完成求解．
23．（2021·江苏扬州市·中考真题）如图，在中，点E在上，且平分，若，，则的面积为________．

【答案】50
【分析】
过点E作EF⊥BC，垂足为F，利用直角三角形的性质求出EF，再根据平行线的性质和角平分线的定义得到∠BCE=∠BEC，可得BE=BC=10，最后利用平行四边形的面积公式计算即可．
【详解】
解：过点E作EF⊥BC，垂足为F，
∵∠EBC=30°，BE=10，
∴EF=BE=5，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DEC=∠BCE，
又EC平分∠BED，即∠BEC=∠DEC，
∴∠BCE=∠BEC，
∴BE=BC=10，
∴四边形ABCD的面积===50，
故答案为：50．

【点睛】
本题考查了平行四边形的性质，30度的直角三角形的性质，角平分线的定义，等角对等边，知识点较多，但难度不大，图形特征比较明显，作出辅助线构造直角三角形求出EF的长是解题的关键．
24．（2021·云南中考真题）已知的三个顶点都是同一个正方形的顶点，的平分线与线段交于点D．若的一条边长为6，则点D到直线的距离为__________．

【答案】3或或或
【分析】
将△ABC放入正方形中，分∠ABC=90°，∠BAC=90°，再分别分AB=BC=6，AC=6，进行解答．
【详解】
解：∵△ABC三个顶点都是同一个正方形的顶点，
如图，若∠ABC=90°，
则∠ABC的平分线为正方形ABCD的对角线，D为对角线交点，
过点D作DF⊥AB，垂足为F，
当AB=BC=6，
则DF=BC=3；
当AC=6，
则AB=BC==，
∴DF=BC=；

如图，若∠BAC=90°，过点D作DF⊥BC于F，
∵BD平分∠ABC，
∴∠ABD=∠CBD，AD=DF，
又∠BAD=∠BFD=90°，BD=BD，
∴△BAD≌△BFD（AAS），
∴AB=BF，
当AB=AC=6，
则BC=，
∴BF=6，CF=，
在正方形ABEC中，∠ACB=45°，
∴△CDF是等腰直角三角形，则CF=DF=AD=；
当BC=6，
则AB=AC==，
同理可得：，

综上：点D到直线AB的距离为：3或或或，
故答案为：3或或或．
【点睛】
本题考查了正方形的性质，角平分线的定义，等腰直角三角形的判定和性质，勾股定理，全等三角形的判定和性质，知识点较多，解题时要结合题意画出符合题意的图形，分情况解答．
25．（2021·江苏南京市·中考真题）如图，在四边形中，．设，则______（用含的代数式表示）．

【答案】
【分析】
由等腰的性质可得：∠ADB=，∠BDC=，两角相加即可得到结论．
【详解】
解：在△ABD中，AB=BD
∴∠A=∠ADB=
在△BCD中，BC=BD
∴∠C=∠BDC=
∵
∴
=
=
=
=
故答案为：．
【点睛】
此题主要考查了等腰三角形的性质和三角形内角和定理，分别求出∠ADB=，∠BDC=是解答本题的关键．
26．（2021·四川资阳市·中考真题）将一张圆形纸片（圆心为点O）沿直径对折后，按图1分成六等份折叠得到图2，将图2沿虚线剪开，再将展开得到如图3的一个六角星．若，则的度数为______．

【答案】135°
【分析】
利用折叠的性质，根据等腰三角形的性质及三角形内角和定理解题．
【详解】
解：连接OC，EO
由折叠性质可得：∠EOC=，EC=DC，OC平分∠ECD
∴∠ECO=
∴∠OEC=180°-∠ECO-∠EOC=135°
即的度数为135°
故答案为：135°

【点睛】
主要在考查折叠的性质，学生动手操作的能力，也考查了等腰三角形的性质及内角和定理，掌握折叠及等腰三角形的性质正确推理计算是解题关键．
27．（2021·浙江金华市·中考真题）如图，菱形的边长为，，将该菱形沿AC方向平移得到四边形，交CD于点E，则点E到AC的距离为____________．

【答案】2
【分析】
首先根据菱形对角线的性质得出AC的长，然后利用菱形对角线平分对角和平移的性质得出等腰 ，过顶点作垂线段EF，利用三线合一得出CF的长，再利用直角三角形30°所对的直角边等于斜边一半和勾股定理列出方程，即可求解．
【详解】
∵∠BAD=60°，
∴连接对角线AC,BD，则AC⊥BD，且AC平分∠BAD,

∴在Rt△ADO中，
利用勾股定理得
又∵AC=2AO,
∴AC= ，
由题可知 =，
∴A’C=;
由平移可知 =∠DAC=30°,而∠DAC=∠DCA,
∴=∠DCA，即==30°，
∴ 是等腰三角形；
过点E作EF⊥AC，垂足为F，如图所示：

则由等腰三角形三线合一可得：A’F=FC=,
在Rt△ECF中， ,设EF=x，则EC=2x，
由勾股定理得：
，解得x=2，
故填：2．
【点睛】
本题考查菱形的性质，等腰三角形三线合一，直角三角形中30°所对的直角边等于斜边一半和勾股定理；菱形对角线互相垂直且平分，一条对角线平分一组对角，熟知概念定理是解题的关键．
28．（2021·浙江绍兴市·中考真题）已知与在同一平面内，点C，D不重合，，，，则CD长为_______．
【答案】，，
【分析】
首先确定满足题意的两个三角形的形状，再通过组合得到四种不同的结果，每种结果分别求解，共得到四种不同的取值；图2、图3、图4均可通过过A点向BC作垂线，构造直角三角形，利用直角三角形的性质可求出相应线段的长，与CD关联即可求出CD的长；图5则是要过D点向BC作垂线，构造直角三角形，解直角三角形即可求解．
【详解】
解：如图1，满足条件的△ABC 与△ABD的形状为如下两种情况，点C，D不重合，则它们两两组合，形成了如图2、图3、图4、图5共四种情况；
如图2，，此时，，由题可知：
，
∴是等边三角形，
∴；
过A点作AE⊥BC，垂足为E点，
在中，∵，
∴,
;
在中，;
∴；
（同理可得到图4和图5中的，，．）
∴．
如图3，，此时，，由题可知：
，
∴是等边三角形，
∴；
过A点作AM⊥BC，垂足为M，
在中，∵，
∴,
;
在中，;
（同理可得到图4和图5中的，，．）
∴CD=；
如图4，由上可知：；
如图5，过D点作DN⊥BC，垂足为N点；
∵，
∴，
∴在中，,
；
∵,
∴在中，;
综上可得：CD的长为，，．
故答案为：，，．




【点睛】
本题主要考查了对几何图形的分类讨论问题，内容涉及到勾股定理、直角三角形30°角所对的直角边等于斜边的一半、解直角三角形、等边三角形等知识，考查了学生对相关概念与性质的理解与应用，本题对综合分析能力要求较高，属于填空题中的压轴题，涉及到了分类讨论与数形结合的思想等．
29．（2021·四川凉山彝族自治州·中考真题）如图，等边三角形ABC的边长为4，的半径为，P为AB边上一动点，过点P作的切线PQ，切点为Q，则PQ的最小值为________．

【答案】3
【分析】
连接OC和PC，利用切线的性质得到CQ⊥PQ，可得当CP最小时，PQ最小，此时CP⊥AB，再求出CP，利用勾股定理求出PQ即可．
【详解】
解：连接QC和PC，
∵PQ和圆C相切，
∴CQ⊥PQ，即△CPQ始终为直角三角形，CQ为定值，
∴当CP最小时，PQ最小，
∵△ABC是等边三角形，
∴当CP⊥AB时，CP最小，此时CP⊥AB，
∵AB=BC=AC=4，
∴AP=BP=2，
∴CP==，
∵圆C的半径CQ=，
∴PQ==3，
故答案为：3．

【点睛】
本题考查了切线的性质，等边三角形的性质，以及勾股定理．此题难度适中，注意掌握辅助线的作法，注意得到当PC⊥AB时，线段PQ最短是关键．
30．（2021·浙江丽水市·中考真题）小丽在“红色研学”活动中深受革命先烈事迹的鼓舞，用正方形纸片制作成图1的七巧板，设计拼成图2的“奔跑者”形象来激励自己．已知图1正方形纸片的边长为4，图2中，则“奔跑者”两脚之间的跨度，即之间的距离是__________．

【答案】
【分析】
先根据图1求EQ与CD之间的距离，再求出BQ，即可得到之间的距离= EQ与CD之间的距离+BQ．
【详解】
解：过点E作EQ⊥BM，则

根据图1图形EQ与CD之间的距离=
由勾股定理得：，解得：；
，解得：
∵
∴
∵EQ⊥BM，
∴
∴
∴之间的距离= EQ与CD之间的距离+BQ
故答案为．
【点睛】
本题考查了平行线间的距离、勾股定理、平行线所分得线段对应成比例相关知识点，能利用数形结合法找到需要的数据是解答此题的关键．
31．（2021·四川成都市·中考真题）如图，在矩形中，，点E，F分别在边上，且，按以下步骤操作：第一步，沿直线翻折，点A的对应点恰好落在对角线上，点B的对应点为，则线段的长为_______；第二步，分别在上取点M，N，沿直线继续翻折，使点F与点E重合，则线段的长为_______．

【答案】1
【分析】
连接AF，NE，NF，证明出△AOE△ADC，利用对应边成比例求出OE=，再根据勾股定理求出的长，利用勾股定理求出EF，再根据折叠的性质，得到NF=NE，最后得出结果．
【详解】
解：如图所示，连接AF，NE，NF，

∵点F与点E重合，
∴MN⊥EF，
设EF与AA’交于点O，由折叠的性质得到OA=OA’=3，
令BF=x，则FC=8-x,
由勾股定理的：
，
∵∠AOE=∠ADC，∠OAE=∠DAC
∴△AOE△ADC，
∴ ，
由勾股定理得到：AC= ，
∴，
∴OE=，
∴OA=，
∴OC=，
∵，
∴ ，
解得：,
∴的长为1．
设B’N=m，B’F=1，则 ，
解得：m=1，则FN= ，
∵EF=，
∴MF=，
∴MN=，
故答案为：1，．
【点睛】
本题主要考查了折叠的性质和勾股定理的应用，关键在于画出图形，利用三角形相似和勾股定理求出各边的长度，特别注意点F与点E重合用到垂直平分线的性质．
32．（2021·浙江金华市·中考真题）如图，在平面直角坐标系中，有一只用七巧板拼成的“猫”，三角形①的边BC及四边形②的边CD都在x轴上，“猫”耳尖E在y轴上．若“猫”尾巴尖A的横坐标是1，则“猫”爪尖F的坐标是___________．

【答案】
【分析】
设大正方形的边长为2a，则大等腰直角三角形的腰长为，中等腰直角三角形的腰长为a，小等腰直角三角形的腰长为，小正方形的边长为，平行四边形的长边为a，短边为，用含有a的代数式表示点A的横坐标，表示点F的坐标，确定a值即可.
【详解】
设大正方形的边长为2a，则大等腰直角三角形的腰长为，中等腰直角三角形的腰长为a，小等腰直角三角形的腰长为，小正方形的边长为，平行四边形的长边为a，短边为，如图，过点F作FG⊥x轴，垂足为G, 点F作FH⊥y轴，垂足为H, 过点A作AQ⊥x轴，垂足为Q,延长大等腰直角三角形的斜边交x轴于点N，交FH于点M，
根据题意，得OC==，CD=a,DQ=，
∵点A的横坐标为1,
∴+a+=1，
∴a=；

根据题意，得FM=PM=，MH=，
∴FH==；
∴MT=2a-，BT=2a-,
∴TN=-a，
∴MN=MT+TN=2a-+-a==，
∵点F在第二象限，
∴点F的坐标为（-，）
故答案为：（-，）．
【点睛】
本题考查了七巧板的意义，合理设出未知数，用未知数表示各个图形的边长，点ＡＡ的横坐标，点Ｆ的坐标是解题的关键．
33．（2021·江苏宿迁市·中考真题）《九章算术》中有一道“引葭赴岸”问题：“仅有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问水深，葭长各几何？”题意是：有一个池塘，其地面是边长为10尺的正方形，一棵芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B'（示意图如图，则水深为__尺．

【答案】12
【分析】
依题意画出图形，设芦苇长AB=AB'=x尺，则水深AC=（x﹣1）尺，因为B'E=10尺，所以B'C=5尺，利用勾股定理求出x的值即可得到答案．
【详解】
解：依题意画出图形，设芦苇长AB=AB'=x尺，则水深AC=（x﹣1）尺，
因为B'E=10尺，所以B'C=5尺，
在Rt△AB'C中，52+（x﹣1）2=x2，
解之得x=13，
即水深12尺，芦苇长13尺．
故答案为：12．
．
【点睛】
此题考查勾股定理的实际应用，正确理解题意，构建直角三角形利用勾股定理解决问题是解题的关键．

三、解答题
34．（2021·浙江温州市·中考真题）如图与的方格都是由边长为1的小正方形组成．图1是绘成的七巧板图案，它由7个图形组成，请按以下要求选择其中一个并在图2、图3中画出相应的格点图形（顶点均在格点上）．

（1）选一个四边形画在图2中，使点为它的一个顶点，并画出将它向右平移3个单位后所得的图形．
（2）选一个合适的三角形，将它的各边长扩大到原来的倍，画在图3中．
【答案】（1）见解析；（2）见解析
【分析】
（1）七巧板中有两个四边形，分别是正方形和平行四边形，根据题意可画出4种图形任意选一种即可，
（2）七巧板中有五个等腰直角三角形，有直角边长 的两个，直角边长2 的两个，直角边长2 的一个，根据题意利用数形结合的思想解决问题即可．
【详解】
解：（1）画法不唯一，当选四边形为正方形时可以是如图1或图2；当四边形式平行四边形时可以是图3或图4．

（2）画法不唯一，
当直角边长为时，扩大即直角边长为利用勾股定理画出直角边长为直角三角形可以是如图5或图6
当直角边长为2时，扩大即直角边长为2利用勾股定理画出直角边长为2直角 三角形可以是如图7或图8等．

【点睛】
本题考查基本作图，平移，二次根式的乘法，以及勾股定理的应用，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．
35．（2021·浙江温州市·中考真题）如图，是的角平分线，在上取点，使．

（1）求证：．
（2）若，，求的度数．
【答案】（1）见解析；（2）35°
【分析】
（1）直接利用角平分线的定义和等边对等角求出，即可完成求证；
（2）先求出∠ADE，再利用平行线的性质求出∠ ABC，最后利用角平分线的定义即可完成求解．

【详解】
解：（1）平分，
．
，
，
，
．
（2），，
．
．
．
平分，
，
即．
【点睛】
本题综合考查了角平分线的定义、等腰三角形的性质、平行线的判定与性质等内容，解决本题的关键是牢记概念与性质，本题的解题思路较明显，属于几何中的基础题型，着重考查了学生对基本概念的理解与掌握．
36．（2021·浙江绍兴市·中考真题）如图，在中，，点D，E分別在边AB，AC上，，连结CD，BE．


（1）若，求，的度数．
（2）写出与之间的关系，并说明理由．
【答案】（1）；；（2），见解析
【分析】
（1）利用三角形的内角和定理求出的大小，再利用等腰三角形的性质分别求出，．
（2）利用三角形的内角和定理、三角形外角的性质和等腰三角形的性质，求出用含分别表示，，即可得到两角的关系．
【详解】
（1），，
．
在中，，
，
，
，
．
．


（2），的关系：．
理由如下：设，．
在中，，
，
．
，
在中，，
．
．
．
．
【点睛】
本题主要通过求解角和两角之间的关系，考查三角形的内角和定理、三角形外角的性质和等腰三角形的性质．三角形的内角和等于 ．三角形的外角等于与其不相邻的两个内角之和．等腰三角形等边对等角．
37．（2021·四川眉山市·中考真题）“眉山水街”走红网络，成为全国各地不少游客新的打卡地！游客小何用无人机对该地一标志建筑物进行拍摄和观测，如图，无人机从处测得该建筑物顶端的俯角为24°，继续向该建筑物方向水平飞行20米到达处，测得顶端的俯角为45°，已知无人机的飞行高度为60米，则这栋建筑物的高度是多少米？（精确到0.1米，参考数据：，，）

【答案】
【分析】
和中有公共直角边CE，根据等腰直角三角形以及锐角三角函数的边角关系解出CE的长度，再用无人机的飞行高度减去CE即可．
【详解】
解：过点C作交AB的延长线于点C，作于点F，如图所示：

在中，，
∴，
在中，，
∴，
解得：，
∴
【点睛】
本题主要考查锐角三角函数解直角三角形，熟练应用锐角三角函数中边与角的关系列出比例是解决本题的关键
38．（2021·四川乐山市·中考真题）如图，已知，，与相交于点，求证：．

【答案】证明见解析
【分析】
根据全等三角形的性质，通过证明，得，结合等腰三角形的性质，即可得到答案．
【详解】
∵，
∴（AAS），
∴，
∴．
【点睛】
本题考查了全等三角形、等腰三角形的知识；解题的关键是熟练掌握全等三角形、等腰三角形的性质，从而完成求解．
39．（2021·重庆中考真题）在等边中，， ，垂足为D，点E为AB边上一点，点F为直线BD上一点，连接EF．

图1 图2 图3
（1）将线段EF绕点E逆时针旋转60°得到线段EG，连接FG．
①如图1，当点E与点B重合，且GF的延长线过点C时，连接DG，求线段DG的长；
②如图2，点E不与点A，B重合，GF的延长线交BC边于点H，连接EH，求证：；
（2）如图3，当点E为AB中点时，点M为BE中点，点N在边AC上，且，点F从BD中点Q沿射线QD运动，将线段EF绕点E顺时针旋转60°得到线段EP，连接FP，当最小时，直接写出的面积．
【答案】（1）①；②见解析；（2）
【分析】
（1）①连接AG，根据题意得出△ABC和△GEF均为等边三角形，从而可证明△GBC≌△GAC，进一步求出AD=3，AG=BG=，然后利用勾股定理求解即可；②以点F为圆心，FB的长为半径画弧，与BH的延长线交于点K，连接KF，先证明出△BFK是顶角为120°的等腰三角形，然后推出△FEB≌△FHK，从而得出结论即可；
（2）利用“胡不归”模型构造出含有30°角的直角三角形，构造出，当N、P、J三点共线的时候满足条件，然后利用相似三角形的判定与性质分别计算出PN与DN的长度，即可得出结论．
【详解】
（1）解：①如图所示，连接AG，
由题意可知，△ABC和△GEF均为等边三角形，
∴∠GFB=60°，
∵BD⊥AC，
∴∠FBC=30°，
∴∠FCB=30°，∠ACG=30°，
∵AC=BC，GC=GC，
∴△GBC≌△GAC（SAS），
∴∠GAC=∠GBC=90°，AG=BG，
∵AB=6，
∴AD=3，AG=BG=，
∴在Rt△ADG中，，
∴；

②证明：以点F为圆心，FB的长为半径画弧，与BH的延长线交于点K，连接KF，如图，
∵△ABC和△GEF均为等边三角形，
∴∠ABC=60°，∠EFH=120°，
∴∠BEF+∠BHF=180°，
∵∠BHF+∠KHF=180°，
∴∠BEF=∠KHF，
由辅助线作法可知，FB=FK，则∠K=∠FBE，
∵BD是等边△ABC的高，
∴∠K=∠DBC=∠DBA=30°，
∴∠BFK=120°，
在△FEB与△FHK中，

∴△FEB≌△FHK（AAS），
∴BE=KH，
∴BE+BH=KH+BH=BK，
∵FB=FK，∠BFK=120°，
∴BK=BF，
即：；

（2）如图1所示，以MP为边构造∠PMJ=30°，∠PJM=90°，则PJ=MP，
∴求的最小值，即为求的最小值，

如图2所示，当运动至N、P、J三点共线时，满足最小，
此时，连接EQ，则根据题意可得EQ∥AD，且EQ=AD，
∴∠MEQ=∠A=60°，∠EQF=90°，
∵∠PEF=60°，
∴∠MEP=∠QEF，
由题意，EF=EP，
∴△MEP≌△QEF（SAS），
∴∠EMP=∠EQF=90°，
又∵∠PMJ=30°，
∴∠BMJ=60°，
∴MJ∥AC，
∴∠PMJ=∠DNP=90°，
∵∠BDC=90°，
∴四边形ODNJ为矩形，NJ=OD，
由题，AD=3，BD=，
∵MJ∥AC，
∴△BMO∽△BAD，
∴，
∴OD=BD=，OM=AD=，
设PJ=x，则MJ=x，OJ=x-，
由题意可知，DN=CD=2，
∴，
解得：，
即：PJ=，
∴，
∴．

【点睛】
本题考查等边三角形的性质，全等三角形的判定与性质以及相似三角形的判定与性质等，理解基本图形的性质，合理构造辅助线是解题关键．
40．（2021·浙江中考真题）已知在中，是的中点，是延长线上的一点，连结．

（1）如图1，若，求的长．
（2）过点作，交延长线于点，如图2所示．若，求证：．
（3）如图3，若，是否存在实数，当时，？若存在，请直接写出的值；若不存在，请说明理由．
【答案】（1）；（2）见解析；（3）存在，
【分析】
（1）先解直角三角形ABC得出，从而得出是等边三角形，再解直角三角形ACP即可求出AC的长，进而得出BC的长；
（2）连结，先利用AAS证出，得出AE=2PE，AC=DE，再得出是等边三角形，然后由SAS得出，得出AE=BC即可得出结论；
（3）过点作，交延长线于点，连接BE，过C作CG⊥AB于G，过E作EN⊥AB于N，由（2）得AE=2AP，DE=AC，再证明，从而得出得出DE=BE，然后利用勾股定理即可得出m的值．
【详解】
（1）解 ，
，
，
，
是等边三角形，

是的中点，
，
在中，，
，
．
（2）证明：连结，
，
，
，
，
，
，
，
又，
，
是等边三角形，

，
，
又，
，
，
．

（3）存在这样的．
过点作，交延长线于点，连接BE，过C作CG⊥AB于G，过E作EN⊥AB于N，则，
，
由（2）得AE=2AP，DE=AC，
∴CG=EN，
∵，
∴AE=BC，
∵∠ANE=∠BGC=90°，
，
∴∠EAN=∠CBG
∵AE=BC，AB=BA，
∴
∴AC=BE，
∴DE=BE，
∴∠EDB=∠EBD=45°，
∴∠DEB=90°，
∴，
∵
∴

【点睛】
本题属于三角形综合题，考查了解直角三角形，全等三角形的性质与判定，等边三角形和等腰三角形的性质、勾股定理，解题的关键是合理添加辅助线，有一定的难度．
41．（2021·江苏连云港市·中考真题）在数学兴趣小组活动中，小亮进行数学探究活动．
（1）是边长为3的等边三角形，E是边上的一点，且，小亮以为边作等边三角形，如图1，求的长；

（2）是边长为3的等边三角形，E是边上的一个动点，小亮以为边作等边三角形，如图2，在点E从点C到点A的运动过程中，求点F所经过的路径长；
（3）是边长为3的等边三角形，M是高上的一个动点，小亮以为边作等边三角形，如图3，在点M从点C到点D的运动过程中，求点N所经过的路径长；

（4）正方形的边长为3，E是边上的一个动点，在点E从点C到点B的运动过程中，小亮以B为顶点作正方形，其中点F、G都在直线上，如图4，当点E到达点B时，点F、G、H与点B重合．则点H所经过的路径长为______，点G所经过的路径长为______．
【答案】（1）1；（2）3；（3）；（4）；
【分析】
（1）由、是等边三角形，，， ，可证即可；
（2）连接，、是等边三角形，可证，可得，又点在处时，，点在A处时，点与重合．可得点运动的路径的长；
（3）取中点，连接，由、是等边三角形，可证，可得．又点在处时，，点在处时，点与重合．可求点所经过的路径的长；
（4）连接CG ,AC ，OB，由∠CGA=90°，点G在以AC中点为圆心，AC为直径的上运动，由四边形ABCD为正方形，BC为边长，设OC=x，由勾股定理即，可求，点G所经过的路径长为长=，点H所经过的路径长为的长．
【详解】
解:（1）∵、是等边三角形，
∴，，．
∴，
∴，
∴，
∴；
（2）连接，
∵、是等边三角形，
∴，，．
∴，
∴，
∴，
∴，，
∵，
∴，
∴，
又点在处时，，点在A处时，点与重合．
∴点运动的路径的长；
（3）取中点，连接，
∴，
∴，
∵，
∴，

∴，
∵、是等边三角形，
∴，，
∴，
∴，
∴，
∴，，
∴，
又点在处时，，点在处时，点与重合，
∴点所经过的路径的长；
（4）连接CG ,AC ，OB，
∵∠CGA=90°，
∴点G在以AC中点为圆心，AC为直径的上运动，
∵四边形ABCD为正方形，BC为边长，
∴∠COB=90°，设OC=x，
由勾股定理即，
∴，
点G所经过的路径长为长=，
点H在以BC中点为圆心，BC长为直径的弧上运动，
点H所经过的路径长为的长度，
∵点G运动圆周的四分之一，
∴点H也运动圆周的四分一，
点H所经过的路径长为的长=，
故答案为；．

【点睛
本题考查等边三角形的性质，三角形全等判定与性质，勾股定理，90°圆周角所对弦是直径，圆的弧长公式，掌握等边三角形的性质，三角形全等判定与性质，勾股定理，90°圆周角所对弦是直径，圆的弧长公式是解题关键．
42．（2021·湖北随州市·中考真题）等面积法是一种常用的、重要的数学解题方法．它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题，在解题中，灵活运用等面积法解决相关问题，可以使解题思路清晰，解题过程简便快捷．

（1）在直角三角形中，两直角边长分别为3和4，则该直角三角形斜边上的高的长为_____，其内切圆的半径长为______；
（2）①如图1，是边长为的正内任意一点，点为的中心，设点到各边距离分别为，，，连接，，，由等面积法，易知，可得_____；（结果用含的式子表示）
②如图2，是边长为的正五边形内任意一点，设点到五边形各边距离分别为，，，，，参照①的探索过程，试用含的式子表示的值．（参考数据：，）

（3）①如图3，已知的半径为2，点为外一点，，切于点，弦，连接，则图中阴影部分的面积为______；（结果保留）
②如图4，现有六边形花坛，由于修路等原因需将花坛进行改造．若要将花坛形状改造成五边形，其中点在的延长线上，且要保证改造前后花坛的面积不变，试确定点的位置，并说明理由．
【答案】（1），1；（2）①；②；（3）①；②见解析．
【分析】
（1）根据等积法解得直角三角形斜边上的高的长，及利用内切圆的性质解题即可；
（2）①先求得边长为的正的面积，再根据解题即可；②设点为正五边形的中心，连接，，过作于，先由正切定义，解得的长，由①中结论知，，继而得到，据此解题；
（3）①由切线性质解得，再由平行线性质及等腰三角形性质解得，根据平行线间的距离相等，及同底等高或等底同高的两个三角形面积相等的性质，可知图中阴影部分的面积等于扇形OBC的面积，最后根据扇形面积公式解题；②连接，过点作交的延长线于点，根据，据此解题．
【详解】
解：（1）直角三角形的面积为：，
直角三角形斜边为：，
设直角三角形斜边上的高为，则

设直角三角形内切圆的半径为，则
，
故答案为：，1；
（2）①边长为的正底边的高为，面积为：

，
故答案为：；
②类比①中方法可知，
设点为正五边形的中心，连接，，

由①得，
过作于，，
故，，
故，从而得到：
．
（3）①是的切线，










过点作

，
是的高，


故答案为：；
②如图，连接，过点作交的延长线于点，则点即为所求，

连接，∵，
∵，
∴，
∴．
【点睛】
本题考查正多边形和圆的知识，涉及含30°角的直角三角形、正切、切线的性质、扇形面积公式、平行线的性质等知识，是重要考点，有难度，掌握相关知识是解题关键．