初中数学湘教版九年级下册1.2 二次函数的图像与性质课堂教学ppt课件

这是一份初中数学湘教版九年级下册1.2 二次函数的图像与性质课堂教学ppt课件，共21页。PPT课件主要包含了二次函数yax²，知识回顾，做一做，新知探究，解配方，开口方向，顶点坐标，对称轴，随堂练习，配方得等内容，欢迎下载使用。

时，图象将发生怎样的变化？
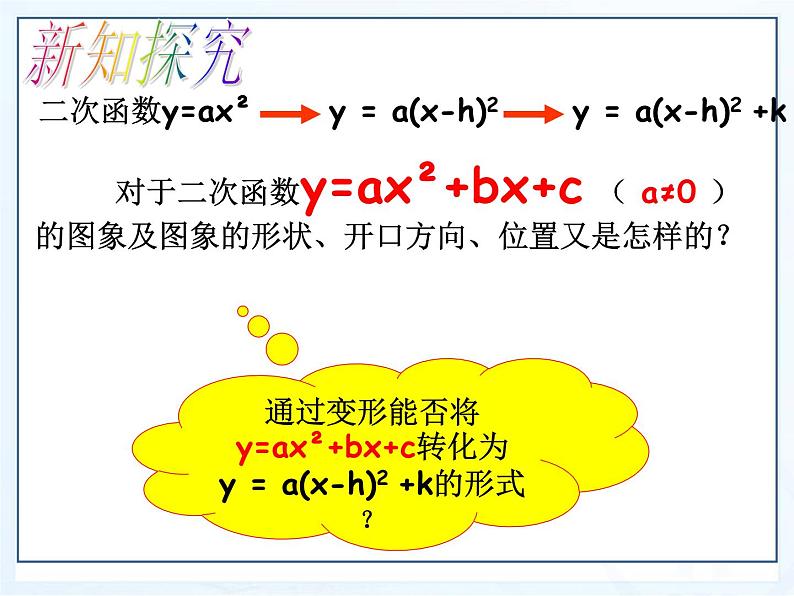
y = a(x-h)2
y = a(x-h)2 +k
一般地，函数y=ax²的图象先向左（当h<0）或向右（当h>0）平移|h|个单位可得y = a(x-h)2的图象；若再向上（当k>0 ）或向下 （当k<0 ）平移|k|个单位可得到y = a(x-h)2 +k的图象。
说出下列抛物线的开口方向、顶点坐标和对称轴
对于二次函数y=ax²+bx+c （ a≠0 ）的图象及图象的形状、开口方向、位置又是怎样的？
通过变形能否将y=ax²+bx+c转化为y = a(x-h)2 +k的形式 ？
时，函数达到最大值（当a<0）或最小值
如何画二次函数 的图象
我们会画y = a(x-h)2 +k的图象了。因此只需把 配方成 的形式就可以了。
故对称轴是直线 ，顶点坐标是
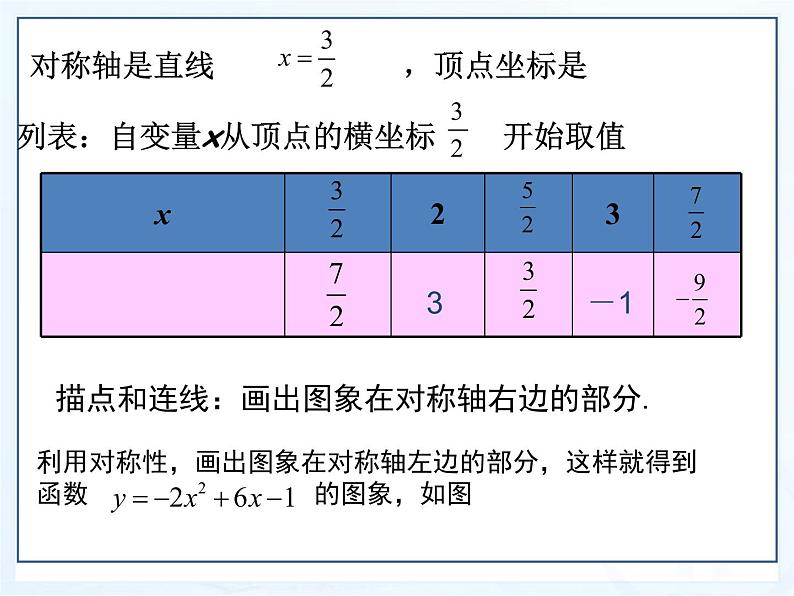
对称轴是直线 ，顶点坐标是
列表：自变量x从顶点的横坐标 开始取值
描点和连线：画出图象在对称轴右边的部分.
从图看出，当x等于多少时，函数 的值最大？这个最大值是多少？
当x等于项点的横坐标 时，函数值 最大。这个最大值等于顶点的纵坐标
从图看出，二次函数 ，当x等于多少时，函数值最小?这个最小值等于多少？
求函数 的最大值
顶点坐标是（2，1），于是当x=2时，y达到最大值1.
1.说出下列抛物线的开口方向、顶点坐标和对称轴并画出它们的图像.
2.求下列二次函数的图象的顶点坐标：
顶点坐标为（－3，4）
3.求下列各个二次函数的最大值或最小值．
4.已知二次函数y= x²+4x–3,请回答下列问题：
（1）、函数 的图象能否由函数 的图象通过平移变换得到？若能，请说出平移的过程，并画出示意图；
（2）、说出函数图象的开口方向、对称轴和顶点坐标。
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
请写出如图所示的抛物线的解析式：