数学人教A版 (2019)5.3 诱导公式第1课时学案

这是一份数学人教A版 (2019)5.3 诱导公式第1课时学案，共7页。学案主要包含了学习目标，自主学习，小试牛刀，经典例题，跟踪训练，当堂达标，课堂小结，参考答案等内容，欢迎下载使用。


【自主学习】
知识点一 公式二
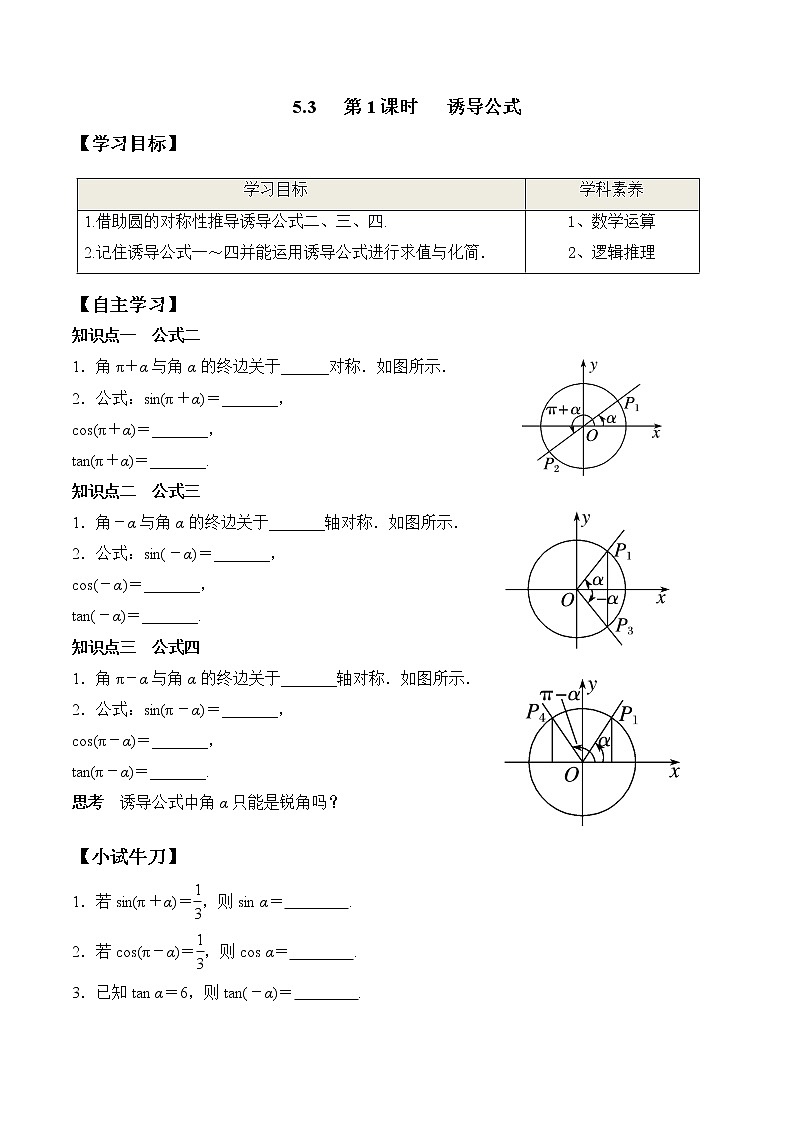
1．角π＋α与角α的终边关于______对称．如图所示．
2．公式：sin(π＋α)＝_______，
cs(π＋α)＝_______，
tan(π＋α)＝_______.
知识点二 公式三
1．角－α与角α的终边关于_______轴对称．如图所示．
2．公式：sin(－α)＝_______，
cs(－α)＝_______，
tan(－α)＝_______.
知识点三 公式四
1．角π－α与角α的终边关于_______轴对称．如图所示．
2．公式：sin(π－α)＝_______，
cs(π－α)＝_______，
tan(π－α)＝_______.
思考 诱导公式中角α只能是锐角吗？
【小试牛刀】
若sin(π＋α)＝eq \f(1,3)，则sin α＝ .
2．若cs(π－α)＝eq \f(1,3)，则cs α＝ .
3．已知tan α＝6，则tan(－α)＝ .
【经典例题】
题型一 利用诱导公式证明
利用诱导公式求任意角三角函数值的步骤
(1)“负化正”：用公式一或三来转化；
(2)“大化小”：用公式一将角化为0°到360°间的角；
(3)“小化锐”：用公式二或四将大于90°的角转化为锐角；
(4)“锐求值”：得到锐角的三角函数后求值．
题型一 给角求值
利用公式求下列三角函数值
cs225° （2） （3） （4）tan(-2040°)
【跟踪训练】1.求值
(1)
(2)sin 1 320°
(3)sin eq \f(5π,6)＋tan eq \f(7π,4)－cs＝ .
题型二 给值(式)求值
解决条件求值问题的策略
(1)解决条件求值问题，首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系．
(2)可以将已知式进行变形向所求式转化，或将所求式进行变形向已知式转化．
例2 (1)已知cs(π－α)＝－eq \f(3,5)，且α是第一象限角，则sin(－2π－α)的值是( )
A.eq \f(4,5) B．－eq \f(4,5) C．±eq \f(4,5) D.eq \f(3,5)
(2)已知，则 .
【跟踪训练】2.若P(－4,3)是角α终边上一点，则eq \f(csα－3π·tanα－2π,sin2π－α)的值为 ．
题型三 化简求值
三角函数式化简的常用方法
(1)利用诱导公式，将任意角的三角函数转化为锐角三角函数．
(2)切化弦：一般需将表达式中的切函数转化为弦函数．
例3 化简
【跟踪训练】3.化简：
(1)eq \f(cs－αtan7π＋α,sinπ－α)；
(2)eq \f(sin1 440°＋α·csα－1 080°,cs－180°－α·sin－α－180°).
【当堂达标】
1.如图所示，角θ的终边与单位圆交于点，则cs(π－θ)的值为( )
A．－eq \f(2\r(5),5) B．－eq \f(\r(5),5)
C.eq \f(\r(5),5) D.eq \f(2\r(5),5)
2．tan 300°＋sin 450°的值是( )
A．－1＋eq \r(3) B．1＋eq \r(3)
C．－1－eq \r(3) D．1－eq \r(3)
3．已知sin(π＋α)＝eq \f(3,5)，且α是第四象限角，那么cs(α－π)的值是( )
A.eq \f(4,5) B．－eq \f(4,5) C．±eq \f(4,5) D.eq \f(3,5)
4.eq \f(cs－585°,sin 495°＋sin－570°)的值等于 ．
5．已知cs(π＋α)＝－eq \f(3,5)，π<α<2π，则sin(α－3π)＋cs(α－π)＝ .
【课堂小结】
1．(1)特殊关系角的终边对称性；(2)诱导公式．
2．方法归纳：函数名不变，符号看象限．
3．常见误区：符号的确定．
【参考答案】
【自主学习】
原点 sin(π+α)=－sinα cs(π+α)=－csα tan(π+α)=tanα
x轴 sin(－α)=－sinα cs(－α)=csα tan(－α)=－tanα
y轴 sin(π-α)=sinα cs(π-α)=－csα tan(π-α)=－tanα
α可以为任意角
【小试牛刀】
－eq \f(1,3) －eq \f(1,3) -6
【经典例题】
例1课本例题
跟踪训练 (1) （2）
（3）
例2 （1）
跟踪训练2
例3
跟踪训练3(1)
(2)
【当堂达标】
C
D
B

5.

学习目标
学科素养
1.借助圆的对称性推导诱导公式二、三、四.
2.记住诱导公式一～四并能运用诱导公式进行求值与化简．
1、数学运算
2、逻辑推理