



所属成套资源:人教版六年级数学下册期中考试复习大全
【期中知识大串讲】第二单元《百分数(二)》章节复习巩固—2021-2022学年数学六年级下册重难点讲义精讲精练(原卷+解析)人教版
展开
这是一份【期中知识大串讲】第二单元《百分数(二)》章节复习巩固—2021-2022学年数学六年级下册重难点讲义精讲精练(原卷+解析)人教版,文件包含期中知识大串讲第二单元《百分数二》章节复习巩固2021-2022学年数学六年级下册重难点讲义精讲精练解析人教版docx、期中知识大串讲第二单元《百分数二》章节复习巩固2021-2022学年数学六年级下册重难点讲义精讲精练原卷人教版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
1.纳税和利息:
储蓄的意义--把消费剩余的钱存入银行,利国利民。
本金--存入银行的钱;
利息--取款时银行除归还本金外,多付的钱。
利率--利息和本金的百分率;
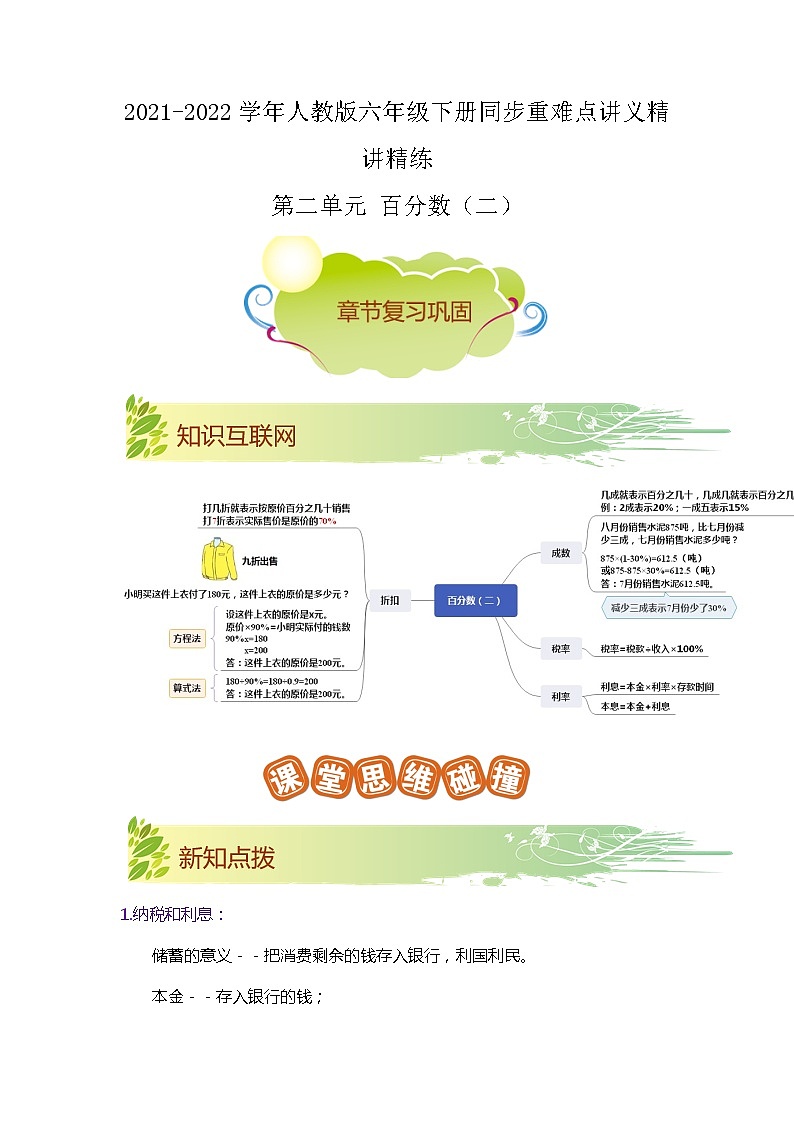
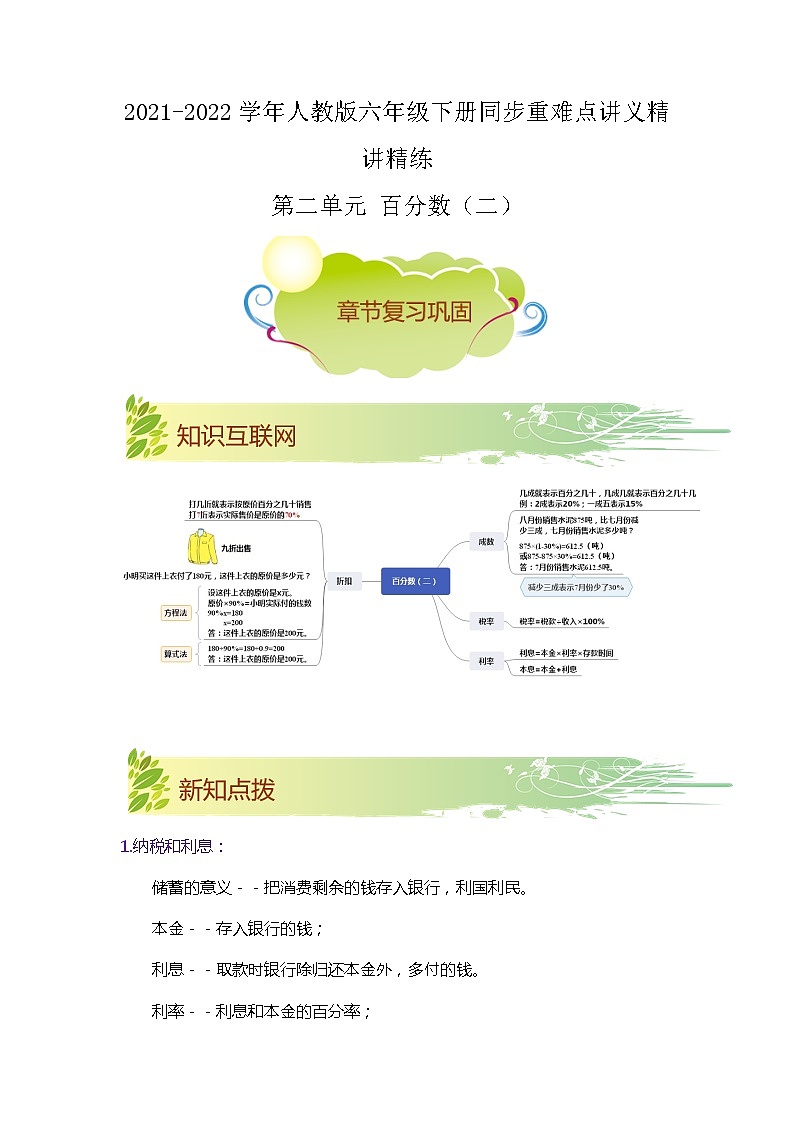
利息计算公式:利息=本金×利率×时间
2.商品有时会降价销售,俗称“折扣”或“打折”出售。“几折”就是表示十分之几,也就是百分之几十。比如说某种商品打“七折”出售,就是按原卖出价的或70%出售;某商品打“六五折”,就是按原卖价的65%出售。
二、方法归纳
1.利息计算公式:利息=本金×利率×时间
利息和=本金+利息
2.应纳税额 = 需要交税的钱 × 税率
3. 现价÷原价=折扣
现价 = 原价 × 折扣(通常写成百分数形式)
原价=现价÷折扣
利润 = 售价 - 成本
利润率=﹙售价-成本﹚÷成本×100%
售价=成本×﹙1+利润率﹚
售价=原价×折扣
定价=成本×﹙1+期望的利润率﹚﹙利润率也称利润百分数,售价也称卖价﹚
=
考点1:折扣问题
【典例分析01】(2021•宁津县)一件商品八折出售比原来少获利200元,那么原来的售价为( )
A.400元B.600元C.800元D.1000 元
【思路引导】八折是指现价是原价的80%,把原价看成单位“1”,它的(1﹣80%)就是现在少获利的钱数200元,由此用除法求出原价。
【完整解答】解:八折=80%,
200÷(1﹣80%)
=200÷20%
=1000(元)
答:这件商品的原价是1000元。
故选:D。
【考察注意点】本题关键是理解打折的含义:打几折,现价就是原价的百分之几十。
【典例分析02】(2021春•怀宁县期末)“五一”假期,某商场进行促销活动,一件上衣打六折后,比原价便宜72元,这件衣服的原价是多少元?
【思路引导】打六折,就是按照原价的60%销售,据此解答即可。
【完整解答】解:72÷(1﹣60%)
=72÷0.4
=180(元)
答:这件衣服的原价是180元。
【考察注意点】根据百分数的意义,解答此题即可。
【变式训练01】(2021•宁津县)爸爸买了一个随身听,原价160元,现在只花了九折的钱,比原价便宜了多少钱?
【思路引导】打九折表示现在的价钱是原价的90%,把原价看作单位“1”,现价比原价便宜的钱就是原价的(1﹣90%),再根据一个数乘百分数的意义解答.
【完整解答】解:160×(1﹣90%)
=160×10%
=160×0.1
=16(元)
答:比原价便宜了16元钱.
【考察注意点】解答此题的关键是找单位“1”,知道少的钱就是原价的1﹣90%.
【变式训练02】(2021•沈丘县)某商场对商品进行促销,广告写道“本店商品一律九折优惠”,一种电器按定价打完折后,发现每台可盈利300元.为了进一步提高这种电器市场占有率,商场决定减少定价的20%,这样仍可盈利60元,这种电器每台定价多少元?进价又是多少元?
【思路引导】根据题意可得:定价×90%=进价+300,定价×(1﹣20%)=进价+60,因此,定价=(300﹣60)÷[90%﹣(1﹣20%)]=2400(元),然后再求出进价即可.
【完整解答】解:(300﹣60)÷[90%﹣(1﹣20%)],
=240÷0.1,
=2400(元);
2400×(1﹣20%)﹣60,
=2400×0.8﹣60,
=1920﹣60,
=1860(元).
答:这种电器每台定价是2400元,进价是1860元.
【考察注意点】此题解答的关键是根据关系式:定价×90%=进价+300,定价×(1﹣20%)=进价+60,进行解答.
考点2:成数问题
【典例分析03】(2020•宝坻区)某景点2019年“五一”期间,游客达到约150万人,比2018年同期大约增加了30万人。这样比2018年同期增加了( )
A.二成B.二成五C.七成五
【思路引导】游客达到约150万人,比2018年同期大约增加了30万人,用150减去30求出2018年同期游客数量;根据成数的意义,用增加的人数除以2018年的人数即可。
【完整解答】解:30÷(150﹣30)
=30÷120
=0.25
0.25=25%=二成五
答:这样比去年同期增加了二成五。
故选:B。
【考察注意点】此题考查了成数的意义,要熟练掌握。
【典例分析04】(2019•德宏州)某景区2017年旅游人数30000人次,2018年的旅游人数比2017年增加了二成五,该景区2018年旅游人数 37500 人次。
【思路引导】把2017年旅游人数看作单位“1”,2018年的旅游人数比2017年增加了二成五,即2018年的旅游人数是2017年人数的(1+25%),用乘法即可求出。
【完整解答】解:30000×(1+25%)
=30000×125%
=37500(人次)
答:该景区2018年旅游人数37500人次。
故答案为:37500。
【考察注意点】本题的关键是找出单位“1”,已知单位“1”的量求它的几分之几是多少用乘法求解。
【变式训练03】(2019秋•新田县期中)比50千克多二成是 60 千克;120米比 200 米少40%
【思路引导】首先理解“成”的概念,“二成”就是20%,把50千克看作单位“1”,增加50千克的20%,增加后的数量是50千克的(1+20%),所以列式为:50×(1+20%);
把要求的长度看成单位“1”,它的(1﹣40%)就是120米,由此用除法求出这个长度。
【完整解答】解:50×(1+20%)
=50×120%
=60(千克)
120÷(1﹣40%)
=120÷60%
=200(米)
答:比50千克多二成是60千克;120米比200米少40%。
故答案为:60,200。
【考察注意点】解答此类问题,首先找清单位“1”,进一步理清解答思路,列式的顺序,从而较好的解答问题。
【变式训练04】(2020秋•怀安县期末)一种计算机现在的售价是3660元,比去年同期降价二成五.去年同期这种计算机的售价是多少元?
【思路引导】降价二成五是指现价比去年的价格降低了25%,把去年的价格看成单位“1”,现价就是去年价格的(1﹣25%),它对应的数量是3660元,求去年的价格用除法.
【完整解答】解:3660÷(1﹣25%),
=3660÷75%,
=4880(元);
答:去年同期这种计算机的售价是4880元.
【考察注意点】本题关键是理解几成几的含义,几成几就是百分之几十几.
考点3:利率问题
【典例分析05】(2020秋•贾汪区期末)吴雪爸爸在2020年6月1日把5000元钱存入银行,定期三年,年利率为4.4%,到期时爸爸可以从银行取回 元.
【思路引导】根据利息的意义,利息=本金×利率×存期,据此求出利息,然后用本金加上利息即可.
【完整解答】解:5000+5000×4.4%×3
=5000+5000×0.044×3
=5000+660
=5660(元)
答:到期时爸爸可以从银行取回5660元.
故答案为:5660.
【考察注意点】这种类型属于利息问题,有固定的计算方法,利息=本金×利率×存期,本息=本金+利息,找清数据与问题,代入公式计算即可.
【典例分析06】(2014秋•东昌府区期末)小王妈11月2日存入银行2000元,定期二年,如果年利率按2.5%计算(10月9日起,对储蓄存款利息所得暂免征收个人所得税),到期时应得利息 100 元.
【思路引导】利息=本金×年利率×时间,本题据此公式解答即可.
【完整解答】解:2000×2.5%×2
=50×2,
=100(元);
答:到期时应得利息100元.
故答案为:100.
【考察注意点】此类利息问题据公式:利息=本金×年利率×时间代入数据计算即可.
【变式训练05】.(2020•齐齐哈尔)李叔叔于2020年5月1日在银行存了活期储蓄1000元,如果每月的利率是0.165%,存款三个月时,可得到利息多少元?本金和利息一共多少元?
【思路引导】本题中,本金是1000元,利率是0.165%,时间是3个月,求利息,根据关系式:利息=本金×利率×时间,求本金和利息,根据关系式:本息=本金+利息,解决问题.
【完整解答】解:1000×0.165%×3=4.95(元)
1000+4.95=1004.95(元)
答:存款三个月时,可得到利息4.95元,本金和利息一共1004.95元.
【考察注意点】此题属于利息问题,考查了关系式:利息=本金×利率×时间,本息=本金+利息.
【变式训练06】(2018秋•渭滨区期末)小林的妈妈在农业银行买了6000元国家建设债券,定期3年,年利率为2.89%,到期她可获得利息多少元?
【思路引导】利用公式:利息=本金×利率×时间,就可以求出利息.
【完整解答】解:6000×2.89%×3=520.2(元);
答:到期她可获得利息520.2元.
【考察注意点】主要考查利息的计算公式:利息=本金×利率×时间.
考点4:税率问题
【典例分析07】(2021春•郑州期中)2018年10月份起,国家将个人所得税征税起点调至5000元。王叔叔11月份收入8000元,如果应纳税额的税率是3%,那么王叔叔应纳税 元,实际收入 元。
【思路引导】先求出王叔叔需要纳税的收入,再根据一个数乘百分数的意义,求出需要纳税的金额,再用原来的收入减去税额就是实际收入。
【完整解答】解:(8000﹣5000)×3%
=3000×3%
=90(元)
8000﹣90=7910(元)
答:王叔叔应纳税90元,实际收入7910元。
故答案为:90,7910。
【考察注意点】本题主要考查了税率问题,正确计算需要纳税的收入是本题解题的关键。
【典例分析08】(2014•永康市模拟)联华超市十二月份的营业额是73000元,如果按营业额的4%缴纳营业税,十二月份应纳税 元.
【思路引导】4%的单位“1”是营业额,即73000元,根据分数乘法的意义,列式即可求出十二月份应纳的税额.
【完整解答】解:73000×4%=2920(元),
答:十二月应纳税2920元.
故答案为:2920.
【考察注意点】此题属于简单的百分数乘法应用题,即找准单位“1”,利用应缴纳营业税=营业额×税率解决问题.
【变式训练07】(2020•徐水区)微信是一款在我国使用非常广泛的社交软件,使用微信支付简单又便捷。微信提现收费规则为:每位注册用户享有1000元免费提现额度,超过部分收取0.1%的手续费。爷爷是微信注册的新用户,现在他要将微信钱包中的2600元全部提现,求爷爷的实际提现金额。
【思路引导】2600元减去1000元,求出收费部分的钱数,乘0.1%求出所需手续费,再用2600减去手续费即为所求。
【完整解答】解:(2600﹣1000)×0.1%
=1600×0.1%
=1.6(元)
2600﹣1.6=2598.4(元)
答:爷爷的实际提现金额是2598.4元。
【考察注意点】解决本题关键是明确1000元不在收费之内的,再根据手续费=本金×费率进行求解。
【变式训练08】(2016春•巴州区校级月考)张华写了一本散文集的稿费5000元,按照个人所得税法规定,稿费收入超过800元的部分按20%交纳个人所得税,他应缴税多少元?
【思路引导】缴税方法是:收入减去800元后再乘20%,先求出超过800元的部分,然后根据百分数乘法的意义,解决问题.
【完整解答】解:(5000﹣800)×20%
=4200×0.2
=840(元)
答:他应缴税840元.
【考察注意点】此题根据关系式:应交税部分×税率=税额.
基础练
一.选择
1.(2020•云梦县)妈妈把5万元钱存入银行,年利率为2.1%,2年后,妈妈能取回多少万元?下面计算方法正确的是( )
A.5×2.1%×2B.5×(1+2.1%×2)
C.5×2.1%+5
【思路引导】利息=本金×利率×存期,本息=本金+利息,据此解答即可。
【完整解答】解:5+5×2.1%×2=5×(1+2.1%×2)
故选:B。
2.(2019秋•宝鸡期末)下面的百分率中,( )有可能超过100%.
A.出勤率
B.及格率
C.增长率
D.黄豆中所含蛋白质的百分率
【思路引导】出勤率是指出勤人数占总人数的百分比,如果全部出勤,则出勤率是100%;
及格率是指及格人数占总人数的百分比,如果全部及格,则及格率是100%;
增长率是指增加的部分占原来的百分数,如果增加的部分大于原来的部分,那么增长率就会大于100%;
黄豆中所含蛋白质的百分率,是部分占整体的百分率,不会达到100%;
据此解答.
【完整解答】解:根据出勤率、及格率、增长率以及黄豆中所含蛋白质的百分率的含义可知:出勤率、及格率最大是100%;
黄豆中所含蛋白质的百分率,是部分占整体的百分率,不会达到100%;
只有增长率会超过100%;
故选:C。
3.(2020•魏县)某商场五一期间举行优惠销售活动,采取“满一百元送二十元,并且连环赠送”的酬宾方式,即顾客每消费满100元(100元可以是现金,也可以是购物券,或二者合计)就送20元购物券,满200元就送40元购物券,依此类推,现有一位顾客第一次就用了16000元购物,并用所得购物券继续购物,那么他购回的商品大约相当于它们原价的( )
A.75%B.80%C.85%D.90%
【思路引导】这位顾客付的钱数是16000元;即其所购买的商品的价值是16000元,根据题意因而可以设他购回的商品大约相当于它们原价的百分比是x.则根据题意可得方程,解即可得答案.
【完整解答】解:根据题意:这位顾客付的钱数是16 000元;
这位顾客所购买的商品的价值是16000元,赠送的购物券的金额是16000×=3200元,3200元赠送的购物券是:3200×20%=640元,640元赠送的购物券是600×=120元,再送购物券20元,
因而用16000元购买的商品的价值是16000+3200+640+120+20=19980元.因而可以设他购回的商品大约相当于它们原价的百分比是x.
则得方程:19980x=16000,
解得:x≈0.8=80%.
故选:B。
4.(2019•郴州模拟)百货商场举行“满200减100”的促销活动,即“满200元减100元,满400元减200元,满600元减300元,…”.如果买一套原价750元的服装,那么实际上相当于打( )折.
A.四B.五C.六
【思路引导】先判断出750元应该减少的钱数,然后用实际付的钱数除以原价求出付钱数是原价的百分之几十,然后根据百分数判断折扣数.
【完整解答】解:750元是满600,减少300元,
(750﹣300)÷750
=450÷750
=60%
就相当于打六折.
故选:C。
二.填空题
5.(2020•炎陵县)小丽去年到银行存了一个定期储蓄1000元,年利率是1.98%利息税是20%,今年到期一年小丽可得本金和税后利息 1015.84 元.
【思路引导】银行的利息税是所得利息的20%,而利息=本金×年利率×时间,由此代入数据计算即可;最后拿到的钱是缴纳利息税后的利息+本金,因此问题容易解决.
【完整解答】解:1000×1.98%×1
=1000×0.0198×1
=19.8(元)
1000+19.8×(1﹣20%)
=1000+19.8×80%
=1000+15.84
=1015.84(元)
答:今年到期一年小丽可得本金和税后利息共 1015.84元.
故答案为:1015.84.
6.(2020•济南)2019年8月,小明的妈妈把4万元存入银行,定期两年,年利率是2.25%,到期时,妈妈从银行连本金带利息一共取回 41800 元.
【思路引导】根据题意,利用公式:本息=本金+本金×利率×时间,把数代入计算即可.
【完整解答】解:4万元=40000元
40000+40000×2.25%×2
=40000+1800
=41800(元)
答:到期时,妈妈从银行连本金带利息一共取回41800元.
故答案为:41800.
7.(2020•吕梁)今年小麦产量比去年增产二成三,表示今年比去年增产 23 %,也就是今年的产量相当于去年的 123 %.
【思路引导】比去年增产二成三是指今年的产量比去年的产量增加23%,今年的产量是去年的1+23%,由此解决问题.
【完整解答】解:今年小麦产量比去年增产二成三,表示今年比去年增产23%,也就是今年的产量相当于去年的123%;
故答案为:23,123.
8.(2019•德宏州)某景区2017年旅游人数30000人次,2018年的旅游人数比2017年增加了二成五,该景区2018年旅游人数 37500 人次。
【思路引导】把2017年旅游人数看作单位“1”,2018年的旅游人数比2017年增加了二成五,即2018年的旅游人数是2017年人数的(1+25%),用乘法即可求出。
【完整解答】解:30000×(1+25%)
=30000×125%
=37500(人次)
答:该景区2018年旅游人数37500人次。
故答案为:37500。
三.判断题
9.(2019秋•会宁县期末)一种商品打“七五折”出售,也就是把这种商品优惠了25%. √ .(判断对错)
【思路引导】七五折是指现价是原价的75%,把原价看成单位“1”,优惠的钱数就是原价的(1﹣75%),由此求解.
【完整解答】解:1﹣75%=25%;
优惠了25%.
故答案为:√.
10.(2013秋•济宁期末)某商品打“九五折”出售,就是降价95%出售. × .(判断对错)
【思路引导】打“九五折”是指现价是原价的95%,那么现价比原价降低了1﹣95%,由此进行判断.
【完整解答】解:“九五折”是指现价是原价的95%;
1﹣95%=5%,降价了5%,不是95%.
故答案为:×.
11.(2013秋•张掖校级期中)一种商品打“七五折”出售,也就是把这种商品优惠了15%. × .(判断对错)
【思路引导】七五折是指现价是原价的75%,把原价看成单位“1”,优惠的钱数就是原价的(1﹣75%),由此求解.
【完整解答】解:1﹣75%=25%;优惠了25%.
故答案为:×.
四.应用题(共4小题)
12.(2020•长沙)利用收集到的存款利率算一算:甲用2000元先存一年定期,到期后连本带息再存一年定期;乙用2000元直接存了二年定期,哪种存款方式到期后获得的利息多?(银行的利率分别为:定期一年3.25%,定期两年3.75%)
【思路引导】根据本金及存期分别按两种储蓄办法计算分析即能确定哪种办法得到的利息多一些:
甲的方法:先存入一年期的,年利率是3.25%,等一年到期时再把本金和利息取出来合在一起,再存入银行一年。则先存一年后可得利息2000×3.25%×1=65元,第二年本金和利息共有2000+65元,加在一起再存一年可得利息(2000+65)×3.25%×1≈67.11元,两年共得利息65+67.11=132.11元。
乙的方法:年利率是3.75%,则存两年后可得利息:2000×3.75%×2=150元;
150元>132.11元,所以直接存两年定期的方式到期后获得的利息多。
【完整解答】解:甲的方法可得利息:
2000×3.25%×1=65(元)
(2000+65)×3.25%×1≈67.11(元)
两年共得利息:65+67.11=132.11(元)
乙的方法可得利息:
2000×3.75%×2=150(元)
150元>132.11元
所以乙的存款方式得到的利息多一些。
答:直接存两年定期的方式到期后获得的利息多。
13.(2020•清丰县)小明把1000元的压岁钱存入银行,存期为3年,年利率为2.75%。到期支取时,小明可得到多少利息?到期时小明一共能取回多少钱?
【思路引导】根据利息=本金×利率×时间,本息=本金+利息,据此解答即可。
【完整解答】解:利息:
1000×2.75%×3
=27.5×3
=82.5(元)
1000+82.5=1082.5(元)
答:小明可得到82.5元利息;到期时小明一共能取回1082.5元。
14.(2020•平舆县)淘气的妈妈给淘气存了1万元的教育存款,存期为三年,年利率为5.40%,到期一次支取.到期时可以拿到多少元?
【思路引导】根据题意,利用公式:本息=本金+本金×利率×存期,把数代入计算即可.
【完整解答】解:1万元=10000元
10000+10000×5.40%×3
=10000+1620
=11620(元)
答:到期时可以拿到11620元.
15.(2020•齐齐哈尔)李叔叔于2020年5月1日在银行存了活期储蓄1000元,如果每月的利率是0.165%,存款三个月时,可得到利息多少元?本金和利息一共多少元?
【思路引导】本题中,本金是1000元,利率是0.165%,时间是3个月,求利息,根据关系式:利息=本金×利率×时间,求本金和利息,根据关系式:本息=本金+利息,解决问题.
【完整解答】解:1000×0.165%×3=4.95(元)
1000+4.95=1004.95(元)
答:存款三个月时,可得到利息4.95元,本金和利息一共1004.95元
提高练
一.选择题
1.(2021•宁津县)一件商品八折出售比原来少获利200元,那么原来的售价为( )
A.400元B.600元C.800元D.1000 元
【思路引导】八折是指现价是原价的80%,把原价看成单位“1”,它的(1﹣80%)就是现在少获利的钱数200元,由此用除法求出原价。
【完整解答】解:八折=80%,
200÷(1﹣80%)
=200÷20%
=1000(元)
答:这件商品的原价是1000元。
故选:D。
2.(2020•中原区)李伟将压岁钱2000元存入银行,存期三年,年利率是2.75%.到期后,银行支付的利息是 ( )元
A.55B.165C.2165
【思路引导】根据利息的计算方法,利息=本金×利率×存期,据此列式解答.
【完整解答】解:2000×2.75%×3
=2000×0.0275×3
=55×3
=165(元)
答:银行支付的利息是165元.
故选:B。
3.(2018•长沙)下面的百分率中,( )可能大于100%.
A.成活率B.出勤率C.增长率
【思路引导】一般来讲,出勤率、成活率、及格率、合格率、正确率能达到100%,增长率能超过100%;出米率、出油率达不到100%;据此解答.
【完整解答】解:成活率是指成活的树的棵数占植树总棵数的百分之几,如果所栽树全部成活,它的成活率最大是100%,同样道理,出勤率最大也是100%,而增长率是指增长的占原来的百分之几,如果增长的比原来的多,这个增长率就大于100%.
故选:C。
4.(2016秋•沈阳期末)下面的百分率中,可以大于100%的是( )
A.成活率B.出勤率C.命中率D.增长率
【思路引导】一般来讲,出勤率、成活率、及格率、合格率、正确率能达到100%,增长率能超过100%;出米率、出油率达不到100%;据此解答.
【完整解答】解:成活率是指成活的树的棵数占植树总棵数的百分之几,如果所栽树全部成活,它的成活率最大是100%,同样道理,出勤率、命中率最大也是100%,而增长率是指增长的占原来的百分之几,如果增长的比原来的多,这个增长率就大于100%.
故选:D。
二.填空题
5.(2019春•麟游县期末)李大爷在3年前把5000元存入银行,定期3年,年利率是5.2%.今年我国西南几省发生特大旱灾,他准备在这笔存款到期时将获得的利息 741 元全部捐给灾区(利息税率为5%).
【思路引导】在此题中,本金是5000元,时间是3年,利率是5.2%,利息税率为5%,求这笔存款到期时将获得的利息,求的是税后利息,运用关系式:利息=本金×年利率×时间×(1﹣5%),解决问题.
【完整解答】解:5000×5.2%×3×(1﹣5%)
=50×5.2×3×0.95
=741(元)
答:他准备在这笔存款到期时将获得的利息741元全部捐给灾区.
故答案为:741.
6.(2018•漳州)(1)根据表中的数据,把下面的折线统计图补充完整.(单位:万元)
(2)第一百货公司2013年的销售额比2012年大约增长了 27.3 %.
(3)从2010年到2013年,第 二 百货公司的销售额增长率较高.第二百货公司预计2014年的销售额比2013年还会增加10%,他们的销售额预计会是 13200 万元.
【思路引导】(1)根据表格数据完成即可;
(2)用第一百货公司2013年的销售额减去2012年的销售额,再除以2012年的销售额即可;
(3)分别计算出从2010年到2013年,两个百货公司的销售额增长率比较即可;
第二百货公司2013年的销售额乘以1+10%即可.
【完整解答】解:(1)
(2)(14000﹣11000)÷11000
=3000÷11000
≈27.3%,
答:第一百货公司2013年的销售额比2012年大约增长了27.3%;
(3)(14000﹣7000)÷7000
=7000÷7000
=100%,
(12000﹣5000)÷5000
=7000÷5000
=140%,
100%<140%
12000×(1+10%)
=12000×110%
=13200(万元)
答:从2010年到2013年,第二百货公司的销售额增长率较高.第二百货公司预计2014年的销售额比2013年还会增加10%,他们的销售额预计会是13200万元.
故答案为:(2)27.3;(3)二,13200.
7.(2013•吴中区)北京一零一中学由于近年生源质量不断提高,特别是师生们的共同努力,使得高考成绩逐年上升.在2001年高考中有59%的考生考上重点大学;2002年高考中有68%的考生考上重点大学;2003年预计将有74%的考生考上重点大学,这三年一零一中学考上重点大学的年平均增长率是 12.04% .
【思路引导】2001﹣﹣2002的增长率是用2002年的百分比减去2001年的百分比除以2001年的百分比;同理可求2002到2003年的增长率,然后求出2001﹣2002的增长率和2002﹣2003的增长率的和,再除以2即可.
【完整解答】解:2001~2002年的增长率为:
(68%﹣59%)÷59%
=9%÷59%
≈15.25%;
2002~2003年的增长率为:
(74%﹣68%)÷68%
=6%÷68%
≈8.82%;
平均增长率为:
(15.25%+8.82%)÷2
=24.07%÷2
≈12.04%.
答:这三年一零一中学考上重点大学的年平均增长率是12.04%.
故答案为:12.04%.
8.(2012•郑州自主招生)2011年4月25日,全国人大常委会公布《中华人民共和国个人所得税法修正案(草案)》,向社会公开征集意见.草案规定,公民全月工薪不超过3000元的部分不必纳税,超过3000元的部分为全月应纳税所得额,此项税款按下表分段累进计算.
依据草案规定,解答下列问题:李工程师的月工薪8000元,则他每月应当纳税 475 元.
【思路引导】分步计算,先求出1500元应交纳1500×5%=75(元),超过1500元至4500元的部分应缴纳(4500﹣1500)×10%=300(元),剩余的应交纳(8000﹣3000﹣1500﹣3000)×20%=100(元),把这三部分部分加起来即可.
【完整解答】解:1500×5%+3000×10%+500×20%,
=75+300+100,
=475(元);
答:这个月他应交纳个人所得税475元.
故答案为:475.
三.判断题
9.(2016春•长沙县期中)一件商品打九折出售,就是降价90%. × .(判断对错)
【思路引导】把原价看作单位“1”,打九折,就是按原价的90%出售,即比原价降低了(1﹣90%),解答即可.
【完整解答】解:一件商品打九折出售,就是按原价的90%出售,也就是比原价低:1﹣90%=10%;所以原题说法错误;
故答案为:×.
10.X的等于Y的(X、Y都不为0),则X比Y多两成。 √ (判断对错)
【思路引导】先根据分数乘法的意义写出乘法算式,然后把X写成用Y表示的式子,X比Y多百分之几=(X﹣Y)÷Y;几成就是百分之几十。
【完整解答】解:X×=Y×
X×÷=Y×÷
X=Y,
(X﹣Y)÷Y
=(Y﹣Y)÷Y
=
=20%
也就是X比Y多两成;原题说法正确。
故答案为:√。
11.一个书包打九折出售,就是说现价比原价降低了90%. × .(判断对错)
【思路引导】根据打折的意义,知道几折就是百分之几十,所以9折就是指售价是原价的90%;把原价看作单位“1”,售价比原价降低了(1﹣90%);据此判断即可.
【完整解答】解:1﹣90%=10%,
答:现价比原价降低了10%.
原题说法错误.
故答案为:×.
四.应用题
12.(2019春•金水区期末)丽丽暑假的假期费用为10000元,她计划把这笔钱分别用于培训学习、暑期游学和储蓄.分配方案是:拿出这笔钱的去参加培训学习,再拿出3000元去暑期游学,余下的存入银行.
(1)请把如图的扇形统计图补充完整.
(2)用于培训学习的有多少元?
(3)将储蓄的钱存入银行三年,年利率为3.5%,三年后到期时丽丽连本带息一共可以取回多少钱?
【思路引导】(1)把总费用看作单位“1”,其中这笔钱的去参加培训学习,根据分数化成百分数的方法得:=60%;再拿出3000元去暑期游学,根据求一个数是另一个数的百分之几,用除法求出暑期游学的费用占总费用的百分之几;然后根据减法的意义,用减法求出储蓄的钱数占总费用的百分之几,据此完成统计图.
(2)根据一个数乘分数的意义,用乘法求出参加培训学习的费用是多少元.
(3)首先用总费用减去参加培训学习和游学的费用求出储蓄的钱数,根据利息的计算方法,利息=本金×利率×存期,然后用利息加上本金即可.据此列式解答.
【完整解答】解:(1)=60%
3000÷10000=30%
1﹣60%﹣30%=10%
作图如下:
(2)10000×=6000(元)
答:用于培训学习的有6000元.
(3)10000﹣6000﹣3000=1000(元)
1000+1000×3.5%×3
=1000+1000×0.035×3
=1000+105
=1105(元)
答:三年后到期时丽丽连本带息一共可以取回1105元.
13.(2019•湘潭模拟)某种商品进货后,零售价定为每件900元,为了适应市场竞争,商品打九折后,再让利40元,仍可获利10%,问这种商品每件的进价是多少元?
【思路引导】先把定价看成单位“1”,九折后的价格是原价的90%,用原价乘90%即可求出九折后的价格,再减去40元,就是最后的售价;此时最后的售价是进价的(1+10%),把进价看成单位“1”,再用除法即可求出进价.
【完整解答】解:900×90%﹣40
=810﹣40
=770(元)
770÷(1+10%)
=770÷110%
=700(元)
答:这种商品每件的进价是700元.
14.(2018春•青川县期末)李叔叔想给女儿存5万元钱,准备存6年,经银行业务员介绍有以下两种方式:第一种是先存5年国债,年利率是5.32%,到期本息和一起再存一年定期,年利率是2.25%;第二种是先存3年国债,年利率是4.92%,到期后本息和一起再存三年定期,年利率是3.25%.李叔叔选哪种方式得到的利息最多?
【思路引导】根据利息=本金×利率×存期,本息=本金+利息,据此分别求出两种方式各得多少利息,然后进行比较即可.
【完整解答】解:第一种:
50000×5.32%×5
=50000×0.0532×5
=2660×5
=13300(元)
(50000+13300)×2.25%×1
=63300×0.0225×1
=1424.25(元)
13300+1424.25=14724.25(元)
第二种:
50000×4.92%×3
=50000×0.0492×3
=2460×3
=7380(元)
(50000+7380)×3.25%×3
=57380×0.0325×3
=1864.85×3
=5594.55(元)
7380+5594.55=12974.55(元),
14724.25>12974.55
答:李叔叔选第一种方式得到的利息最多.
五.解答题
15.(2021•灵石县)某工厂去年用电350万千瓦时,今年比去年节电二成五,今年用电多少万千瓦时?
【思路引导】今年比去年节电二成五,是指今年的用电量比去年少25%,是把去年的用电量看成单位“1”,今年的用电量就是去年的(1﹣25%),用去年的用电量乘上这个分率,就是今年的用电量.
【完整解答】解:350×(1﹣25%)
=350×75%
=262.5(万千瓦时)
答:今年用电262.5万千瓦时.
16.(2020•丰润区)某县前年秋粮产量为2.8万吨,去年比前年增产三成.去年秋粮产量是多少万吨?
【思路引导】增产三成就是增加原来产量的30%,即去年产量是前年的1+30%=130%,把前年产量看作单位“1”,运用分数乘法意义即可解答.
【完整解答】解:2.8×(1+30%)
=2.8×130%
=3.64(万吨)
答:去年秋粮产量为3.64万2010年
2011年
2012年
2013年
第一百货公司
7000
9800
11000
14000
第二百货公司
5000
7800
10000
12000
级数
全月应纳税所得额
税率
1
不超过1500元的部分
5%
2
超过1500元至4500元的部分
10%
3
超过4500元至9000元的部分
20%
…
…
相关试卷
这是一份【期中知识大串讲】第一单元《位置与方向(一)》章节复习巩固—2021-2022学年数学三年级下册重难点讲义精讲精练(原卷+解析)人教版,文件包含期中知识大串讲第一单元《位置与方向一》章节复习巩固2021-2022学年数学三年级下册重难点讲义精讲精练解析人教版doc、期中知识大串讲第一单元《位置与方向一》章节复习巩固2021-2022学年数学三年级下册重难点讲义精讲精练原卷人教版doc等2份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。
这是一份【期中知识大串讲】第二单元《观察物体(二)》章节复习巩固—2021-2022学年数学四年级下册重难点讲义精讲精练(原卷+解析)人教版,文件包含期中知识大串讲第二单元《观察物体二》章节复习巩固2021-2022学年数学四年级下册重难点讲义精讲精练解析人教版doc、期中知识大串讲第二单元《观察物体二》章节复习巩固2021-2022学年数学四年级下册重难点讲义精讲精练原卷人教版doc等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
这是一份【期中知识大串讲】第二单元《因数和倍数》章节复习巩固—2021-2022学年数学五年级下册重难点讲义精讲精练(原卷+解析)人教版,文件包含期中知识大串讲第二单元《因数和倍数》章节复习巩固2021-2022学年数学五年级下册重难点讲义精讲精练解析人教版docx、期中知识大串讲第二单元《因数和倍数》章节复习巩固2021-2022学年数学五年级下册重难点讲义精讲精练原卷人教版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。










