专题2.4 二次函数与幂函数-2022年高考数学一轮复习核心素养大揭秘学案

这是一份专题2.4 二次函数与幂函数-2022年高考数学一轮复习核心素养大揭秘学案，文件包含专题24二次函数与幂函数解析版doc、专题24二次函数与幂函数原卷版doc等2份学案配套教学资源，其中学案共25页， 欢迎下载使用。

【考纲要求】
1. 掌握二次函数的图象与性质，会求二次函数的最值(值域)、单调区间．
2．了解幂函数的概念．
3．结合函数y＝x，y＝x2，y＝x3，y＝eq \f(1,x)，y＝x eq \s\up4(\f(1,2)) 的图象，了解它们的变化情况.
【命题趋势】
1. 二次函数的图象和性质，经常与其他知识综合考查．
2．幂函数的图象和性质，很少单独出题．
3．二次函数的综合应用，经常与导数、不等式综合考查.
【核心素养】
本讲内容主要考查直观想象和逻辑推理的核心素养.
【素养清单•基础知识】
1．二次函数解析式的三种形式
一般式：f(x)＝ax2＋bx＋c(a≠0)；
顶点式：f(x)＝a(x－h)2＋k(a≠0)；
两根式：f(x)＝a(x－x1)(x－x2)(a≠0)．
2．二次函数的图象与性质
二次函数系数的特征
(1)二次函数y＝ax2＋bx＋c(a≠0)中，系数a的正负决定图象的开口方向及开口大小；
(2)－eq \f(b,2a)的值决定图象对称轴的位置；
(3)c的取值决定图象与y轴的交点；
(4)b2－4ac的正负决定图象与x轴的交点个数．
3．幂函数的概念
一般地，形如y＝xα(α∈R)的函数称为幂函数，其中底数x是自变量，α为常数．
幂函数的特征
(1)自变量x处在幂底数的位置，幂指数α为常数；
(2)xα的系数为1；
(3)只有一项．
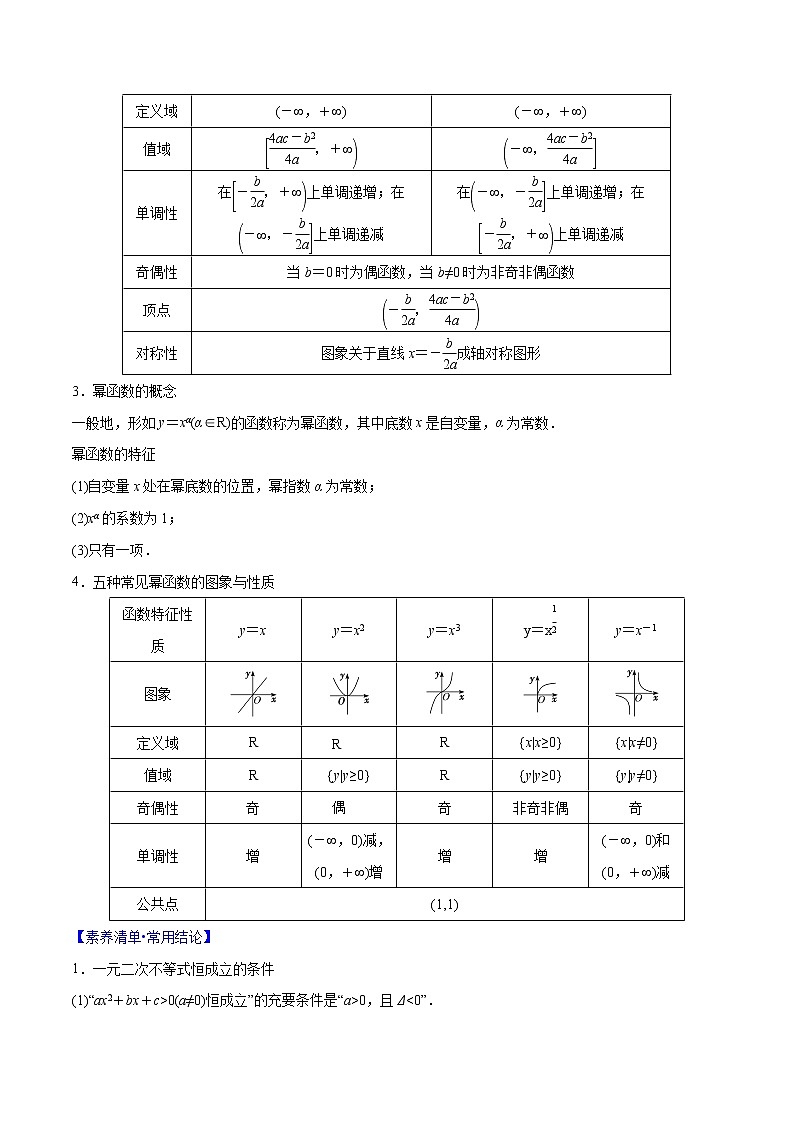
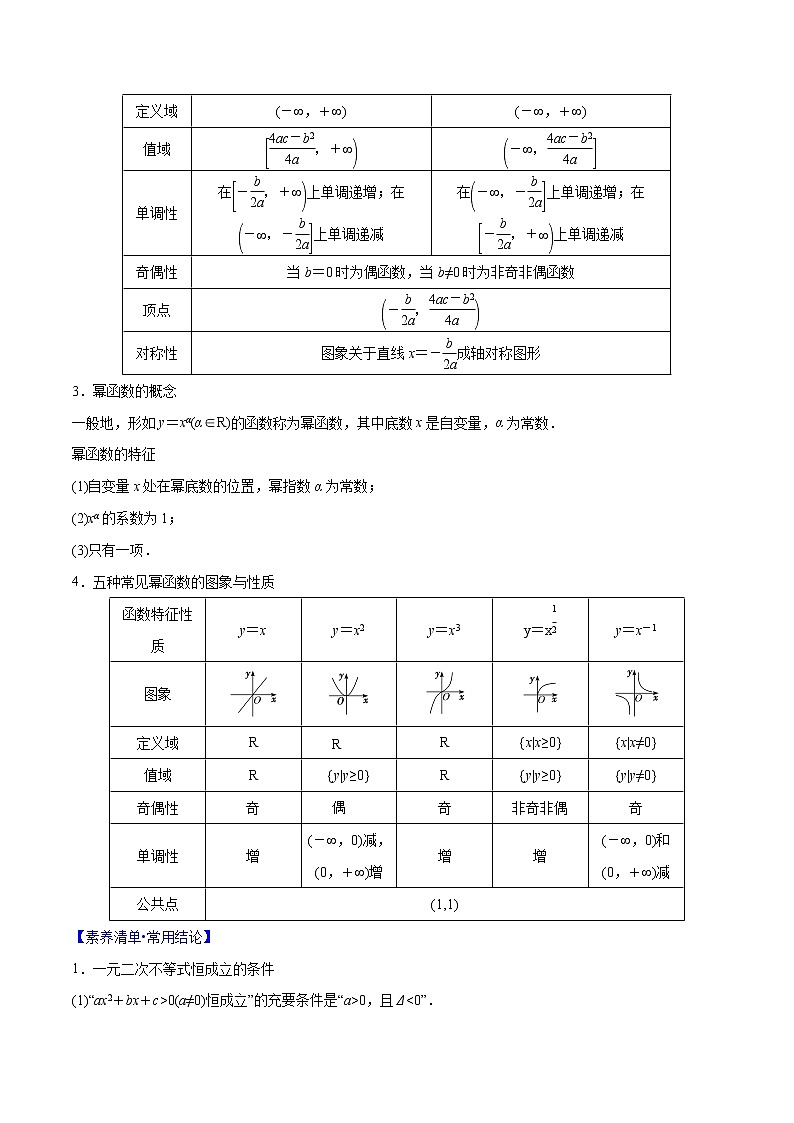
4．五种常见幂函数的图象与性质
【素养清单•常用结论】
1．一元二次不等式恒成立的条件
(1)“ax2＋bx＋c>0(a≠0)恒成立”的充要条件是“a>0，且Δ<0”．
(2)“ax2＋bx＋c<0(a≠0)恒成立”的充要条件是“a<0，且Δ<0”．
2．二次函数在闭区间上的最值
设二次函数f(x)＝ax2＋bx＋c(a>0)，闭区间为[m，n]．
(1)当－eq \f(b,2a)≤m时，最小值为f(m)，最大值为f(n)；
(2)当m<－eq \f(b,2a)≤eq \f(m＋n,2)时，最小值为feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(b,2a)))，最大值为f(n)；
(3)当eq \f(m＋n,2)<－eq \f(b,2a)≤n时，最小值为feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(b,2a)))，最大值为f(m)；
(4)当－eq \f(b,2a)>n时，最小值为f(n)，最大值为f(m)．
3.对于形如f(x)＝xeq \f(n,m)(其中m∈N*，n∈Z，m与n互质)的幂函数：
(1)当n为偶数时，f(x)为偶函数，图象关于y轴对称；
(2)当m，n都为奇数时，f(x)为奇函数，图象关于原点对称；
(3)当m为偶数时，x>0(或x≥0)，f(x)是非奇非偶函数，图象只在第一象限(或第一象限及原点处)．
【真题体验】
1.【2019年高考全国Ⅱ卷理数】设函数的定义域为R，满足，且当时，．若对任意，都有，则m的取值范围是（ ）
A．
B．
C．
D．
【答案】B
【解析】∵，．
∵时，；
∴时，，；
∴时，，，
如图：

当时，由解得，，
若对任意，都有，则.
则m的取值范围是.
故选B.
【名师点睛】本题考查了函数与方程，二次函数.解题的关键是能够得到时函数的解析式，并求出函数值为时对应的自变量的值.
2.【2018年高考浙江】已知λ∈R，函数f(x)=，当λ=2时，不等式f(x)<0的解集是___________．若函数f(x)恰有2个零点，则λ的取值范围是___________．
【答案】(1,4)；
【解析】由题意得或，所以或，即，故不等式f(x)<0的解集是
当时，，此时，即在上有两个零点；当时，，由在上只能有一个零点得.综上，的取值范围为.
【名师点睛】根据分段函数，转化为两个不等式组，分别求解，最后求并集.先讨论一次函数零点的取法，再对应确定二次函数零点的取法，即得参数的取值范围.已知函数有零点求参数取值范围常用的方法和思路：
(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；
(2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；
(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．
3.【2018年高考天津理数】已知，函数若关于的方程恰有2个互异的实数解，则的取值范围是______________.
【答案】
【解析】分类讨论：
当时，方程即，整理可得：，很明显不是方程的实数解，则；
当时，方程即，整理可得：，很明显不是方程的实数解，则.
令，其中，，则原问题等价于函数与函数有两个不同的交点，求的取值范围.结合对勾函数和函数图象平移的规律绘制函数的图象，同时绘制函数的图象如图所示，考查临界条件，结合观察可得，实数的取值范围是.

【名师点睛】本题的核心是考查函数的零点问题，由题意分类讨论和两种情况，然后绘制函数图象，数形结合即可求得最终结果.函数零点的求解与判断方法包括：
(1)直接求零点：令f(x)＝0，如果能求出解，则有几个解就有几个零点．
(2)零点存在性定理：利用定理不仅要函数在区间[a，b]上是连续不断的曲线，且f(a)·f(b)＜0，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点．
(3)利用图象交点的个数：将函数变形为两个函数的差，画两个函数的图象，看其交点的横坐标有几个不同的值，就有几个不同的零点.
4.【2017年高考浙江】若函数f(x)=x2+ ax+b在区间[0，1]上的最大值是M，最小值是m，则M – m（ ）
A．与a有关，且与b有关 B．与a有关，但与b无关
C．与a无关，且与b无关 D．与a无关，但与b有关
【答案】B
【解析】因为最值在中取，所以最值之差一定与无关.
故选B．
【名师点睛】对于二次函数的最值或值域问题，通常先判断函数图象对称轴与所给自变量闭区间的关系，结合图象，当函数图象开口向上时，若对称轴在区间的左边，则函数在所给区间内单调递增；若对称轴在区间的右边，则函数在所给区间内单调递减；若对称轴在区间内，则函数图象顶点的纵坐标为最小值，区间端点距离对称轴较远的一端取得函数的最大值．
5.【2017年高考山东理数】已知当时，函数的图象与的图象有且只有一个交点，则正实数的取值范围是（ ）
A． B．
C． D．
【答案】B
【解析】当时，，在时单调递减，且，在时单调递增，且，此时有且仅有一个交点；
当时，，在上单调递增，所以要有且仅有一个交点，需.
故选B.
【名师点睛】已知函数有零点求参数的取值范围常用的方法和思路：
（1）直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数的取值范围；
（2）分离参数法：将参数分离，转化成求函数值域的问题加以解决；
（3）数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．
【考法拓展•题型解码】
考法一 幂函数的图象和性质
归纳总结：幂函数的性质与图象特征的关系
(1)幂函数的形式是y＝xα(α∈R)，其中只有一个参数α，因此只需一个条件即可确定其解析式．
(2)判断幂函数y＝xα(α∈R)的奇偶性时，当α是分数时，一般将其先化为根式，再判断．
(3)若幂函数y＝xα在(0，＋∞)上单调递增，则α＞0，若在(0，＋∞)上单调递减，则α＜0.
【例1】 (1)已知幂函数f(x)＝(n2＋2n－2)·xn2－3n(n∈Z)在(0，＋∞)上是减函数，则n的值为( )
A．－3 B．1
C．2 D．1或2
【答案】B
【解析】由于f(x)为幂函数，所以n2＋2n－2＝1，解得n＝1或n＝－3.当n＝1时，f(x)＝x－2＝eq \f(1,x2)在(0，＋∞)上是减函数；当n＝－3时，f(x)＝x18在(0，＋∞)上是增函数．故n＝1符合题意．故选B．
(2)幂函数y＝f(x)的图象过点(4,2)，则幂函数y＝f(x)的图象是( )
【答案】C
【解析】因为幂函数y＝f(x)的图象过点(4,2)，所以f(x)＝x eq \s\up4(\f(1,2)) .故选C
(3)已知幂函数f(x)满足f(8)＝4，则f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2) ,2)))__________f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(3) ,3)))(填＞，＝或＜)．
【答案】＞
【解析】设f(x)＝xα(α为常数)，又f(8)＝4，所以4＝8α，所以α＝eq \f(2,3).于是f(x)＝x eq \s\up4(\f(2,3)) ，显然该函数是偶函数，且在区间(0，＋∞)上是增函数，在(－∞，0)上是减函数．所以f eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(3),3)))＝f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),3)))考法二 求二次函数的解析式
解题技巧
求二次函数解析式的方法
根据已知条件确定二次函数解析式，一般用待定系数法，方法如下：
【例2】 (1)已知二次函数f(x)满足f(2)＝－1，f(－1)＝－1，且f(x)的最大值是8，则此二次函数的解析式为__________．
(2)已知二次函数f(x)的二次项系数为a，且不等式f(x)>－2x的解集为(1,3)．若方程f(x)＋6a＝0有两个相等的根，则f(x)的解析式为__________．
【答案】见解析
【解析】 (1)设f(x)＝ax2＋bx＋c(a≠0)．
由题意得eq \b\lc\{\rc\ (\a\vs4\al\c1(4a＋2b＋c＝－1，,a－b＋c＝－1，,\f(4ac－b2,4a)＝8，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(a＝－4，,b＝4，,c＝7，))
所以所求二次函数的解析式为f(x)＝－4x2＋4x＋7.
(2)因为f(x)＋2x>0的解集为(1,3)，
设f(x)＋2x＝a(x－1)(x－3)，且a<0，
所以f(x)＝a(x－1)(x－3)－2x＝ax2－(2＋4a)x＋3a.①
由方程f(x)＋6a＝0，得ax2－(2＋4a)x＋9a＝0.②
因为方程②有两个相等的根，
所以Δ＝[－(2＋4a)]2－4a·9a＝0，解得a＝1或a＝－eq \f(1,5).
由于a<0，舍去a＝1.将a＝－eq \f(1,5)代入①式得f(x)＝－eq \f(1,5)x2－eq \f(6,5)x－eq \f(3,5)为所求函数f(x)的解析式．
考法三 二次函数的图象和性质
归纳总结
(1)对于函数f(x)＝ax2＋bx＋c，若是二次函数，就隐含a≠0，当题目未说明是二次函数时，就要分a＝0和a≠0两种情况讨论．
(2)二次函数最值问题的解法：抓住“三点一轴”数形结合，三点是指区间两个端点和中点，一轴指的是对称轴，结合配方法，根据函数的单调性及分类讨论的思想即可完成．
(3)由不等式恒成立求参数的取值范围，常用的方法有两种，一是分离参数法，转化为求函数最值问题，其依据是a≥f(x)恒成立⇔a≥f(x)max，a≤f(x)恒成立⇔a≤f(x)min；二是判别式法，转化依据是f(x)>0(a≠0)恒成立的充要条件是eq \b\lc\{\rc\ (\a\vs4\al\c1(a>0，,Δ<0，))f(x)<0(a≠0)恒成立的充要条件是eq \b\lc\{\rc\ (\a\vs4\al\c1(a<0，,Δ<0.))
(4)要注意数形结合思想的应用，尤其是给定区间上的二次函数最值问题，先“定性”(作草图)，再“定量”(看图求解)，事半功倍．
【例3】 (1)如图是二次函数y＝ax2＋bx＋c图象的一部分，图象过点A(－3,0)，对称轴为x＝－1.给出下面四个结论：
①b2＞4ac；②2a－b＝1；③a－b＋c＝0；④5a其中正确的结论是( )
A．②④ B．①④
C．②③ D．①③
【答案】B
【解析】因为二次函数的图象与x轴交于两点，所以b2－4ac>0，即b2>4ac，①正确；对称轴为x＝－1，即－eq \f(b,2a)＝－1,2a－b＝0，②错误；结合图象知，当x＝－1时，y>0，即a－b＋c>0，③错误；由对称轴为x＝－1知b＝2a，又函数图象开口向下，所以a<0，所以5a<2a，即5a(2)若函数f(x)＝x2＋2ax＋3在区间[－4,6]上是单调函数，则实数a的取值范围为__________．
【答案】(－∞，－6]∪[4，＋∞)
【解析】由于函数f(x)的图象开口向上，对称轴是x＝－a，所以要使f(x)在[－4,6]上是单调函数，应有－a≤－4或－a≥6，即a≤－6或a≥4.
(3)若函数f(x)＝x2－3x－4的定义域为[0，m]，值域为eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(25,4)，－4))，则m的取值范围是__________．
【答案】eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3,2)，3))
【解析】函数f(x)图象的对称轴为x＝eq \f(3,2)，且f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)))＝－eq \f(25,4)，f(3)＝f(0)＝－4，由二次函数的图象知m的取值范围为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3,2)，3)).
【例4】 (1)(2017·浙江卷)若函数f(x)＝x2＋ax＋b在区间[0,1]上的最大值是M，最小值是m，则M－m( )
A．与a有关，且与b有关 B．与a有关，但与b无关
C．与a无关，且与b无关 D．与a无关，但与b有关
【答案】B
【解析】设x1，x2分别是函数f(x)在[0,1]上的最小值点与最大值点，则m＝xeq \\al(2,1)＋ax1＋b，M＝xeq \\al(2,2)＋ax2＋b.所以M－m＝xeq \\al(2,2)－xeq \\al(2,1)＋a(x2－x1)，显然此值与a有关，与b无关．故选B．
(2)当x∈(1,2)时，不等式x2＋mx＋4<0恒成立，则m的取值范围是__________．
【答案】(－∞，－5]
【解析】设f(x)＝x2＋mx＋4，当x∈(1,2)时，f(x)<0恒成立⇔eq \b\lc\{\rc\ (\a\vs4\al\c1(f1≤0，,f2≤0))⇒eq \b\lc\{\rc\ (\a\vs4\al\c1(m≤－5，,m≤－4))⇒m≤－5.
【易错警示】
易错点 忽视一元二次方程中对Δ的讨论
【典例】 已知关于x的方程x2－2mx＋4m2－6＝0的两根为α，β，则(α－1)2＋(β－1)2的取值范围是__________．
【错解】：(－∞，15]
【错因分析】：在已知一元二次方程的根的情况时，忽略了隐含的Δ≥0以及韦达定理的内容，导致最小值的遗漏．
【正解】：【答案】[6－4eq \r(2)，15]
【解析】由题意得eq \b\lc\{\rc\ (\a\vs4\al\c1(α＋β＝2m，,αβ＝4m2－6，))所以(α－1)2＋(β－1)2＝(α＋β)2－2αβ－2(α＋β)＋2＝(2m)2－2(4m2－6)－4m＋2＝－4m2－4m＋14＝－4eq \b\lc\(\rc\)(\a\vs4\al\c1(m＋\f(1,2)))2＋15.又因为Δ≥0，即(－2m)2－4(4m2－6)≥0，所以－eq \r(2)≤m≤eq \r(2)，所以当m＝eq \r(2)时，(α－1)2＋(β－1)2的最小值为6－4eq \r(2)；
当m＝－eq \f(1,2)时，(α－1)2＋(β－1)2取得最大值15.故所求的取值范围为[6－4eq \r(2)，15]．
【误区防范】
一元二次方程与二次函数问题中的注意点
(1)已知一元二次方程有根时，就隐含了条件“Δ≥0”以及韦达定理．
(2)求二次函数最值时要考虑图象的开口方向；对称轴与所给区间的位置关系，区间端点值的大小等问题．
(3)要学会一元二次方程、二次函数、一元二次不等式三者之间的正确转换．
【跟踪训练】 已知函数f(x)＝x2＋2mx＋2m＋3(m∈R)，若关于x的方程f(x)＝0有实数根，且两根分别为x1，x2，则(x1＋x2)·x1x2的最大值为( )
A．1 B．2
C．3 D．4
【答案】B
【解析】 因为x1＋x2＝－2m，x1x2＝2m＋3，
所以(x1＋x2)·x1x2＝－2m(2m＋3)＝－4eq \b\lc\(\rc\)(\a\vs4\al\c1(m＋\f(3,4)))2＋eq \f(9,4).
又Δ＝4m2－4(2m＋3)≥0，所以m≤－1或m≥3.
因为t＝－4eq \b\lc\(\rc\)(\a\vs4\al\c1(m＋\f(3,4)))2＋eq \f(9,4)在m∈(－∞，－1)上单调递增，在m∈[3，＋∞)上单调递减，所以m＝－1时t取最大值为2.
所以(x1＋x2)·x1x2的最大值为2.故选B．
【递进题组】
1．若幂函数f(x)＝mxα的图象经过点Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,4)，\f(1,2)))，则m和α的值分别为( )
A．eq \f(1,4)，eq \f(1,2) B．eq \f(1,2)，eq \f(1,4)
C．1，eq \f(1,2) D．eq \f(1,2)，1
【答案】C
【解析】 根据函数f(x)＝mxα为幂函数，所以m＝1，根据图象经过点Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,4)，\f(1,2)))，则有α＝eq \f(1,2).
2．已知函数f(x)＝ex－1，g(x)＝－x2＋4x－3.若有f(a)＝g(b)，则b的取值范围为( )
A．[2－eq \r(2)，2＋eq \r(2)] B．(2－eq \r(2)，2＋eq \r(2))
C．[1,3] D．(1,3)
【答案】B
【解析】 由题意可知，f(x)＝ex－1>－1，g(x)＝－x2＋4x－3＝－(x－2)2＋1≤1.若有f(a)＝g(b)，则g(b)∈(－1,1]，即－b2＋4b－3>－1，解得2－eq \r(2)3．已知abc>0，则二次函数f(x)＝ax2＋bx＋c的图象可能是( )
【答案】D
【解析】 A项，因为a<0，－eq \f(b,2a)<0，所以b<0，又因为abc>0，所以c>0，而f(0)＝c<0，故A项错误；B项，因为a<0，－eq \f(b,2a)>0，所以b>0，又因为abc>0，所以c＜0，而f(0)＝c>0，故B项错误；C项，因为a>0，－eq \f(b,2a)<0，所以b>0，又因为abc>0，所以c>0，而f(0)＝c<0，故C项错误；D项，因为a>0，－eq \f(b,2a)>0，所以b<0，因为abc>0，所以c<0，而f(0)＝c<0，故D项正确．
4．已知函数f(x)＝－x2＋3x＋4的定义域为[－2,2]，则f(x)的值域为__________．
【答案】eq \b\lc\[\rc\](\a\vs4\al\c1(－6，\f(25,4)))
【解析】 函数f(x)＝－x2＋3x＋4图象的对称轴为x＝eq \f(3,2)，所以在区间[－2,2]上，函数的最大值为f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)))＝－eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)))2＋3×eq \f(3,2)＋4＝eq \f(25,4)，函数的最小值为f(－2)＝－(－2)2＋3×(－2)＋4＝－6，所以函数的值域为eq \b\lc\[\rc\](\a\vs4\al\c1(－6，\f(25,4))).
5．设函数f(x)＝ax2－2x＋2，对于满足1＜x<4的一切x值都有f(x)>0，则实数a的取值范围是__________．
【答案】 eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，＋∞))
【解析】 由f(x)>0，即ax2－2x＋2>0，x∈(1,4)，得a>－eq \f(2,x2)＋eq \f(2,x)在(1,4)上恒成立．令g(x)＝－eq \f(2,x2)＋eq \f(2,x)＝－2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)－\f(1,2)))2＋eq \f(1,2)，eq \f(1,x)∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,4)，1))，所以g(x)max＝g(2)＝eq \f(1,2)，所以要使f(x)>0在(1,4)上恒成立，则a>eq \f(1,2).
【考卷送检】
一、选择题
1．已知幂函数f(x)＝k2·xa＋1的图象过点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，\f(\r(2),2)))，则k＋a＝( )
A．eq \f(1,2) B．－eq \f(3,2)
C．eq \f(1,2)或－eq \f(3,2) D．2
【答案】C
【解析】因为f(x)＝k2·xa＋1是幂函数，所以k2＝1，所以k＝±1.又f(x)的图象过点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，\f(\r(2),2)))，所以eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))a＋1＝eq \f(\r(2),2)，所以a＋1＝eq \f(1,2)，所以a＝－eq \f(1,2)，所以k＋a＝±1－eq \f(1,2)＝－eq \f(3,2)或eq \f(1,2).
2．抛物线y＝ax2＋bx＋c的顶点在第一象限，与x轴的两个交点分别位于原点两侧，则a，b，c的符号为( )
A．a＜0，b＜0，c＜0B．a＜0，b＞0，c＞0
C．a＜0，b＜0，c＞0D．a＜0，b＞0，c＜0
【答案】B
【解析】 由题意知抛物线开口向下，故a<0.由抛物线与x轴的两个交点分别位于原点两侧得eq \f(c,a)<0，所以c>0.再由顶点在第一象限得－eq \f(b,2a)>0，所以b>0.
3．若a＝2－ eq \s\up4(\f(3,2)) ，b＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,5)))3，c＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))3，则a，b，c的大小关系是( )
A．a＜b＜c B．c＜a＜b
C．b＜c＜a D．b＜a＜c
【答案】C
【解析】 a＝2－ eq \s\up4(\f(3,2)) ＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)))3，根据函数y＝x3是R上的增函数，且eq \f(2,5)＜eq \f(1,2)＜eq \f(\r(2),2)，得
eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,5)))3＜eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))3＜eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)))3，即b＜c＜a.
4．二次函数f(x)＝ax2＋bx＋5满足条件f(－1)＝f(3)，则f(2)的值为( )
A．5 B．6
C．8 D．与a，b的值有关
【答案】A
【解析】 因为函数f(x)＝ax2＋bx＋5满足条件f(－1)＝f(3)，所以f(x)＝ax2＋bx＋5的图象关于x＝eq \f(－1＋3,2)＝1对称，则f(2)＝f(0)＝5.故选A．
5．对任意的x∈[－2,1]，不等式x2＋2x－a≤0恒成立，则实数a的取值范围是( )
A．(－∞，0] B．(－∞，3]
C．[0，＋∞) D．[3，＋∞)
【答案】D
【解析】 设f(x)＝x2＋2x－a(x∈[－2,1])，其对称轴为x＝－1，所以当x＝1时，f(x)取得最大值3－a，所以3－a≤0，解得a≥3.故选D．
6．(2019·杭州测试)若函数f(x)＝x2－2x＋1在区间[a，a＋2]上的最小值为4，则实数a的取值集合为( )
A．[－3,3] B．[－1,3]
C．{－3,3} D．{－1，－3,3}
【答案】C
【解析】 因为函数f(x)＝x2－2x＋1＝(x－1)2的图象的对称轴为直线x＝1，f(x)在区间[a，a＋2]上的最小值为4，所以当a≥1时，f(x)min＝f(a)＝(a－1)2＝4，a＝－1(舍去)或a＝3；当a＋2≤1，即a≤－1时，f(x)min＝f(a＋2)＝(a＋1)2＝4，a＝1(舍去)或a＝－3；当a＜1＜a＋2，即－1＜a＜1时，f(x)min＝f(1)＝0≠4.故a的取值集合为{－3,3}．故选C．
二、填空题
7．已知函数f(x)＝x eq \s\up4(\f(1,2)) ，且f(2x－1)【答案】 eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(1,2)，＋∞))
【解析】 f(x)＝x eq \s\up4(\f(1,2)) 在[0，＋∞)上是单调递增的，且f(2x－1)8．二次函数的图象过点(0,1)，对称轴为x＝2，最小值为－1，则它的解析式为________．
【答案】 f(x)＝eq \f(1,2)(x－2)2－1
【解析】 依题意可设f(x)＝a(x－2)2－1(a＞0)，又其图象过点(0,1)，所以4a－1＝1，所以a＝eq \f(1,2)，所以f(x)＝eq \f(1,2)(x－2)2－1.
9．(2019·河北师大附中期中)若函数f(x)＝mx2－2x＋3在[－1，＋∞)上单调递减，则实数m的取值范围为________．
【答案】 [－1,0]
【解析】 当m＝0时，f(x)＝－2x＋3在R上单调递减，符合题意；当m≠0时，函数f(x)＝mx2－2x＋3在[－1，＋∞)上单调递减，只需对称轴x＝eq \f(1,m)≤－1且m＜0，解得－1≤m＜0，综上，实数m的取值范围为[－1,0]．
三、解答题
10．已知函数f(x)＝x2＋2ax＋3，x∈[－4,6]．
(1)当a＝－2时，求f(x)的最值；
(2)求实数a的取值范围，使y＝f(x)在区间[－4,6]上是单调函数．
【答案】见解析
【解析】 (1)当a＝－2时，f(x)＝x2－4x＋3＝(x－2)2－1，因为x∈[－4，6]，所以f(x)在[－4,2]上单调递减，在[2,6]上单调递增，所以f(x)的最小值是f(2)＝－1，又f(－4)＝35，f(6)＝15，故f(x)的最大值是35.
(2)由于函数f(x)的图象开口向上，对称轴是x＝－a，所以要使f(x)在[－4,6]上是单调函数，应有－a≤－4或－a≥6，即a≤－6或a≥4，故a的取值范围是(－∞，－6]∪[4，＋∞)．
11．(2019·杭州模拟)已知值域为[－1，＋∞)的二次函数f(x)满足f(－1＋x)＝f(－1－x)，且方程f(x)＝0的两个实根x1，x2满足|x1－x2|＝2.
(1)求f(x)的表达式；
(2)函数g(x)＝f(x)－kx在区间[－1,2]上的最大值为g(2)，最小值g(－1)，求实数k的取值范围．
【答案】见解析
【解析】 (1)由f(－1＋x)＝f(－1－x)可得f(x)的图象关于直线x＝－1对称，设f(x)＝a(x＋1)2＋h＝ax2＋2ax＋a＋h(a≠0)，由函数f(x)的值域为[－1，＋∞)，可得h＝－1，根据根与系数的关系可得x1＋x2＝－2，x1x2＝1＋eq \f(h,a)，所以|x1－x2|＝eq \r(x1＋x22－4x1x2)＝eq \r(－\f(4h,a))＝2，解得a＝1，所以f(x)＝x2＋2x.
(2)由题意得函数g(x)在区间[－1,2]上单调递增，又g(x)＝f(x)－kx＝x2－(k－2)x.所以g(x)的对称轴方程为x＝eq \f(k－2,2)，则eq \f(k－2,2)≤－1，即k≤0，故k的取值范围为(－∞，0]．
12．已知幂函数f(x)＝(－2m2＋m＋2)xm＋1为偶函数．
(1)求f(x)的解析式；
(2)若函数h(x)＝f(x)＋ax＋3－a≥0在区间[－2,2]上恒成立，求实数a的取值范围．
【答案】见解析
【解析】 (1)由f(x)为幂函数知－2m2＋m＋2＝1，得m＝1或m＝－eq \f(1,2).当m＝1时，f(x)＝x2，符合题意；当m＝－eq \f(1,2)时，f(x)＝x eq \s\up4(\f(1,2)) ，不合题意，舍去．所以f(x)＝x2.
(2)h(x)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(a,2)))2－eq \f(a2,4)－a＋3，令h(x)在[－2,2]上的最小值为g(a)．
①当－eq \f(a,2)＜－2，即a＞4时，g(a)＝h(－2)＝7－3a≥0，所以a≤eq \f(7,3).又a＞4，所以a不存在；
②当－2≤－eq \f(a,2)≤2，即－4≤a≤4时，g(a)＝heq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(a,2)))＝－eq \f(a2,4)－a＋3≥0，所以－6≤a≤2.又－4≤a≤4，所以－4≤a≤2；
③当－eq \f(a,2)＞2，即a＜－4时，g(a)＝h(2)＝7＋a≥0，所以a≥－7.又a＜－4，所以－7≤a＜－4.综上可知，a的取值范围为[－7,2]．
13．(2019·襄阳五中期中)已知a，b，c，d都是常数，a＞b，c＞d.若f(x)＝2 019－(x－a)(x－b)的零点为c，d，则下列不等式正确的是( )
A．a＞c＞b＞d B．a＞b＞c＞d
C．c＞d＞a＞b D．c＞a＞b＞d
【答案】D
【解析】 因为f(x)＝2 019－(x－a)(x－b)，所以f(a)＝f(b)＝2 019，c，d为函数f(x)的零点，且a＞b，c＞d，所以可在平面直角坐标系中作出函数f(x)的大致图象，如图所示，由图可知c＞a＞b＞d.故选D．

解析式
f(x)＝ax2＋bx＋c(a>0)
f(x)＝ax2＋bx＋c(a<0)
图象
定义域
(－∞，＋∞)
(－∞，＋∞)
值域
eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(4ac－b2,4a)，＋∞))
eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(4ac－b2,4a)))
单调性
在eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(b,2a)，＋∞))上单调递增；在eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(b,2a)))上单调递减
在eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(b,2a)))上单调递增；在eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(b,2a)，＋∞))上单调递减
奇偶性
当b＝0时为偶函数，当b≠0时为非奇非偶函数
顶点
eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(b,2a)，\f(4ac－b2,4a)))
对称性
图象关于直线x＝－eq \f(b,2a)成轴对称图形
函数特征性质
y＝x
y＝x2
y＝x3
y＝x eq \s\up4(\f(1,2))
y＝x－1
图象
定义域
R
eq \a\vs4\al(R)
R
{x|x≥0}
{x|x≠0}
值域
R
{y|y≥0}
R
{y|y≥0}
{y|y≠0}
奇偶性
奇
eq \a\vs4\al(偶)
奇
非奇非偶
奇
单调性
增
(－∞，0)减，
(0，＋∞)增
增
增
(－∞，0)和
(0，＋∞)减
公共点
(1,1)