专题3.3 三角函数的图像和性质-2022年高考数学一轮复习核心素养大揭秘学案

这是一份专题3.3 三角函数的图像和性质-2022年高考数学一轮复习核心素养大揭秘学案，文件包含专题33三角函数的图像和性质解析版doc、专题33三角函数的图像和性质原卷版doc等2份学案配套教学资源，其中学案共38页， 欢迎下载使用。
第三篇 三角函数与解三角形
专题3.3 三角函数的图像和性质
【考纲要求】
1. 能画出y＝sin x，y＝cos x，y＝tan x的图象，了解三角函数的周期性．
2．理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值以及与x轴的交点等)，理解正切函数在区间内的单调性．
3．了解函数y＝Asin(ωx＋φ)的物理意义；能画出y＝Asin(ωx＋φ)的图象，了解参数A，ω，φ对函数图象变化的影响．
4．体会三角函数是描述周期变化现象的重要函数模型，会用三角函数解决一些简单的实际问题.
【命题趋势】
1.三角函数的图象，主要考查三角函数的图象变换、三角函数解析式的求法及三角函数图象的应用．
2．三角函数的性质是高考的必考内容，常与三角函数的图象结合，主要考查三角函数的周期性、单调性、最值、奇偶性、对称性．
3．高考中常以选择、填空题的形式考查三角函数关系式、三角函数诱导公式、三角函数的奇偶性及对称性，属于中低档题．
4．以解答题的形式考查三角函数的单调性、最值，常与平面向量、解三角形及三角恒等变换相结合.
【核心素养】
本讲内容主要考查数学运算和直观想象的核心素养。
【素养清单•基础知识】
1．用五点法作正弦函数和余弦函数的简图
(1)“五点法”作图原理：
在正弦函数y＝sin x，x∈[0,2π]的图象上，五个关键点是：(0,0)，，(π，0)，，(2π，0)．
在余弦函数y＝cos x，x∈[0,2π]的图象上，五个关键点是：(0,1)，，(π，－1)，，(2π，1).
函数y＝sin x，x∈[0，2π]，y＝cos x，x∈[0，2π]的五个关键点的横坐标是零点和极值点(最值点).
(2)五点法作图的三步骤：列表、描点、连线(注意光滑)．
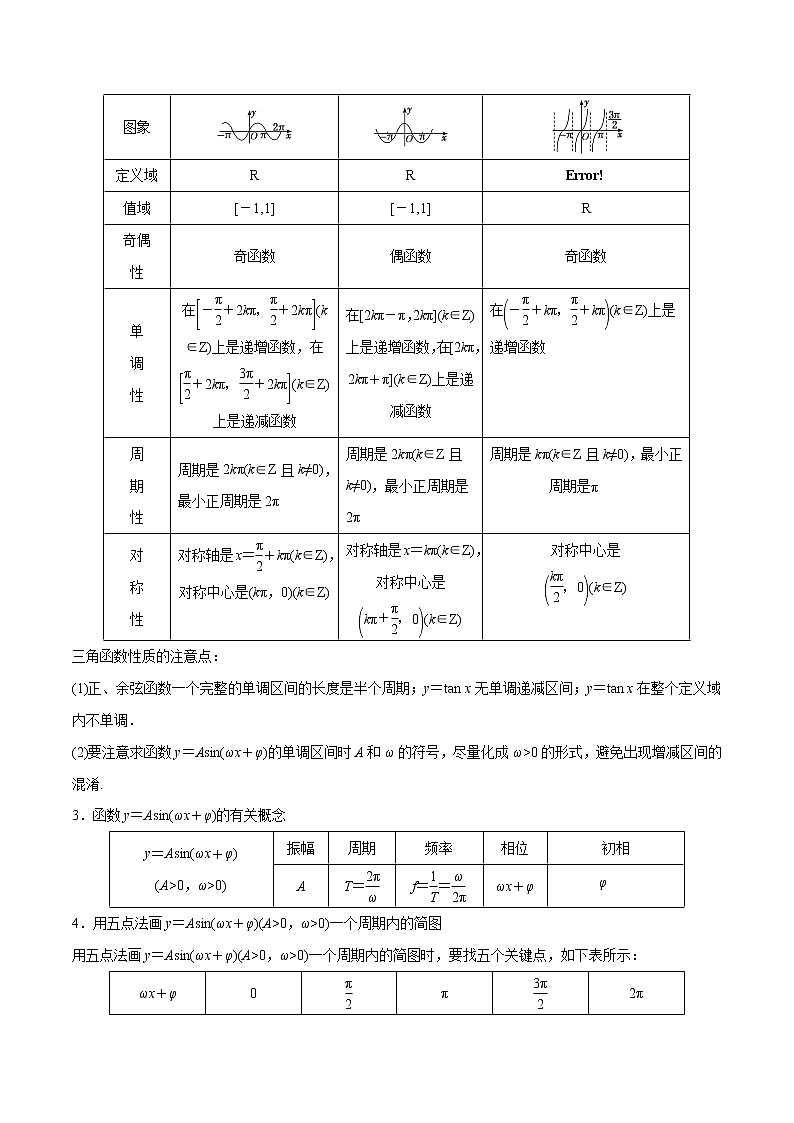
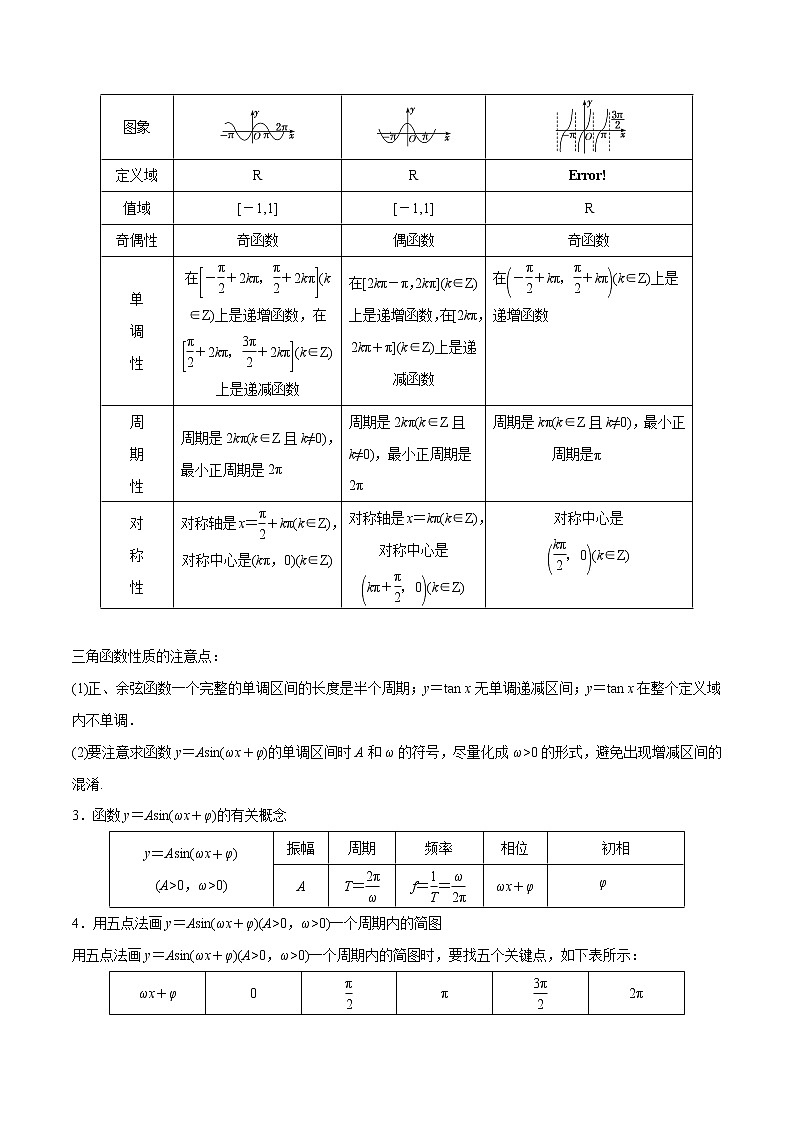
2．正弦、余弦、正切函数的图象与性质
函数
y＝sin x
y＝cos x
y＝tan x
图象



定义域
R
R

值域
[－1,1]
[－1,1]
R
奇偶性
奇函数
偶函数
奇函数
单
调
性
在(k∈Z)上是递增函数，在(k∈Z)上是递减函数
在[2kπ－π，2kπ](k∈Z)上是递增函数，在[2kπ，2kπ＋π](k∈Z)上是递减函数
在(k∈Z)上是递增函数
周
期
性
周期是2kπ(k∈Z且k≠0)，最小正周期是2π
周期是2kπ(k∈Z且k≠0)，最小正周期是2π
周期是kπ(k∈Z且k≠0)，最小正周期是
对
称
性
对称轴是x＝＋kπ(k∈Z)，对称中心是(kπ，0)(k∈Z)
对称轴是x＝kπ(k∈Z)，对称中心是(k∈Z)
对称中心是
(k∈Z)

三角函数性质的注意点：
(1)正、余弦函数一个完整的单调区间的长度是半个周期；y＝tan x无单调递减区间；y＝tan x在整个定义域内不单调．
(2)要注意求函数y＝Asin(ωx＋φ)的单调区间时A和ω的符号，尽量化成ω>0的形式，避免出现增减区间的混淆.
3．函数y＝Asin(ωx＋φ)的有关概念
y＝Asin(ωx＋φ)
(A>0，ω>0)
振幅
周期
频率
相位
初相
A
T＝
f＝＝
ωx＋φ

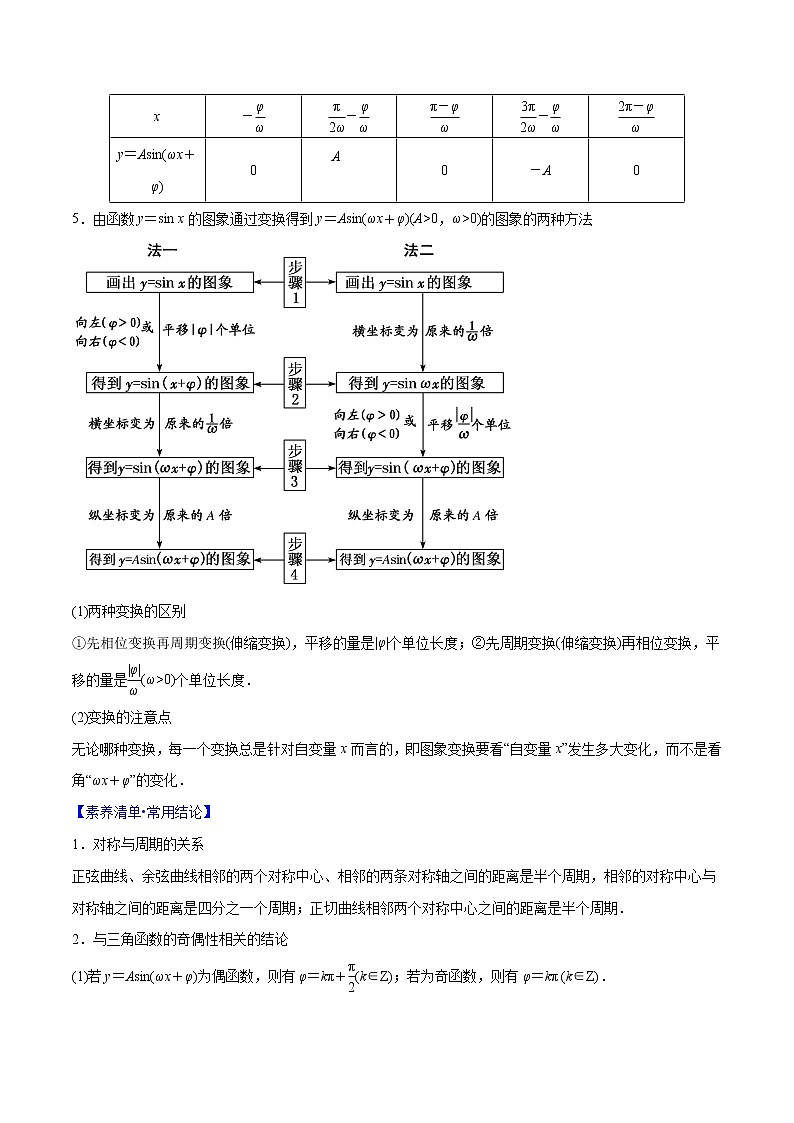
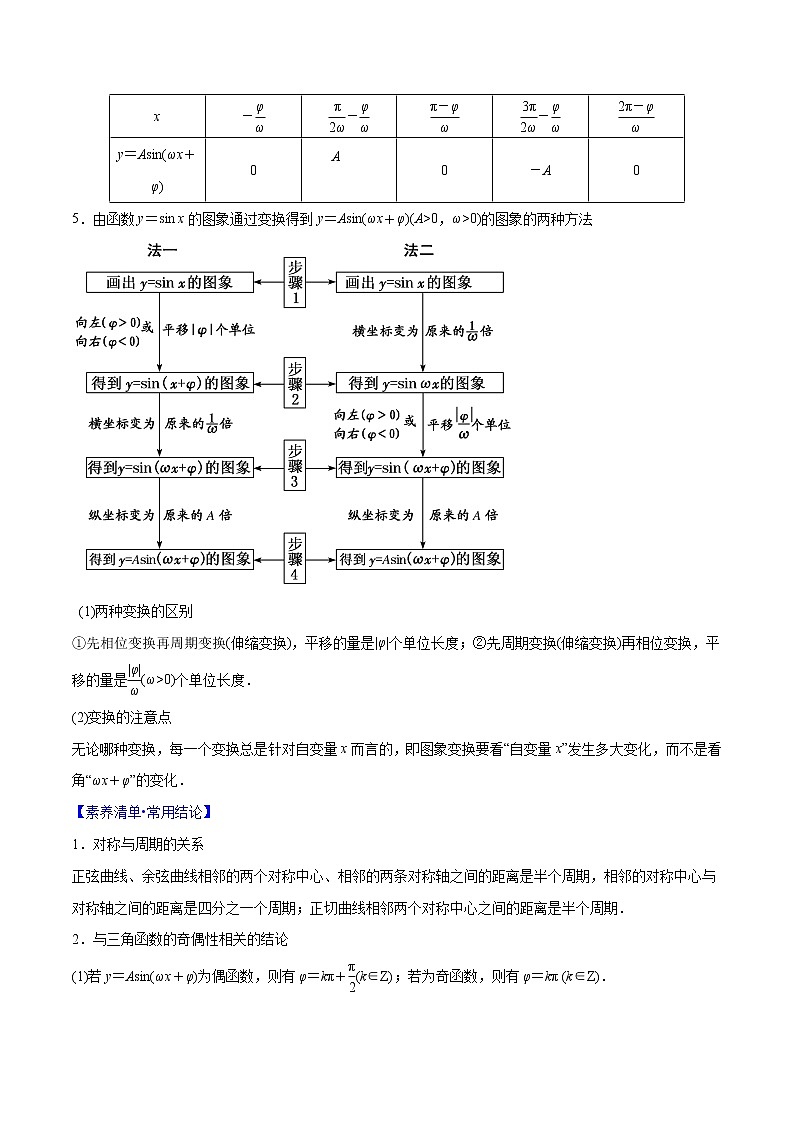
4．用五点法画y＝Asin(ωx＋φ)(A>0，ω>0)一个周期内的简图
用五点法画y＝Asin(ωx＋φ)(A>0，ω>0)一个周期内的简图时，要找五个关键点，如下表所示：
ωx＋φ
0

π

2π
x
－
－

－

y＝Asin(ωx＋φ)
0

0
－A
0
5．由函数y＝sin x的图象通过变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种方法

(1)两种变换的区别
①先相位变换再周期变换(伸缩变换)，平移的量是|φ|个单位长度；②先周期变换(伸缩变换)再相位变换，平移的量是(ω>0)个单位长度．
(2)变换的注意点
无论哪种变换，每一个变换总是针对自变量x而言的，即图象变换要看“自变量x”发生多大变化，而不是看角“ωx＋φ”的变化．
【素养清单•常用结论】
1．对称与周期的关系
正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是四分之一个周期；正切曲线相邻两个对称中心之间的距离是半个周期．
2．与三角函数的奇偶性相关的结论
(1)若y＝Asin(ωx＋φ)为偶函数，则有φ＝kπ＋(k∈Z)；若为奇函数，则有φ＝kπ (k∈Z)．
(2)若y＝Acos(ωx＋φ)为偶函数，则有φ＝kπ(k∈Z)；若为奇函数，则有φ＝kπ＋ (k∈Z)．
(3)若y＝Atan(ωx＋φ)为奇函数，则有φ＝kπ(k∈Z)．
【真题体验】
1.【2019年高考全国Ⅰ卷理数】函数f(x)=在的图像大致为（ ）
A． B．
C． D．
【答案】D
【解析】由，得是奇函数，其图象关于原点对称，排除A．又，排除B，C，故选D．
【名师点睛】本题考查函数的性质与图象，渗透了逻辑推理、直观想象和数学运算素养，采取性质法或赋值法，利用数形结合思想解题．解答本题时，先判断函数的奇偶性，得是奇函数，排除A，再注意到选项的区别，利用特殊值得正确答案．
2.【2019年高考全国Ⅰ卷理数】关于函数有下述四个结论：
①f(x)是偶函数 ②f(x)在区间（，）单调递增
③f(x)在有4个零点 ④f(x)的最大值为2
其中所有正确结论的编号是（ ）
A．①②④ B．②④
C．①④ D．①③
【答案】C
【解析】为偶函数，故①正确．
当时，，它在区间单调递减，故②错误．
当时，，它有两个零点：；当时，
，它有一个零点：，故在有个零点：，故③错误．
当时，；当时，，又为偶函数，的最大值为，故④正确．
综上所述，①④正确，故选C．
【名师点睛】本题也可画出函数的图象（如下图），由图象可得①④正确．

3. 【2019年高考全国Ⅱ卷理数】下列函数中，以为周期且在区间(，)单调递增的是（ ）
A．f(x)=|cos2x| B．f(x)=|sin2x|
C．f(x)=cos|x| D．f(x)=sin|x|
【答案】A
【解析】作出因为的图象如下图1，知其不是周期函数，排除D；
因为，周期为，排除C；
作出图象如图2，由图象知，其周期为，在区间(，)单调递增，A正确；
作出的图象如图3，由图象知，其周期为，在区间(，)单调递减，排除B，
故选A．

图1

图2

图3
【名师点睛】本题主要考查三角函数的图象与性质，渗透直观想象、逻辑推理等数学素养，画出各函数图象，即可作出选择．本题也可利用二级结论：①函数的周期是函数周期的一半；②不是周期函数.
4.【2019年高考全国Ⅲ卷理数】设函数=sin（）(＞0)，已知在有且仅有5个零点，下述四个结论：
①在（）有且仅有3个极大值点
②在（）有且仅有2个极小值点
③在（）单调递增
④的取值范围是[)
其中所有正确结论的编号是（ ）
A．①④ B．②③
C．①②③ D．①③④
【答案】D
【解析】①若在上有5个零点，可画出大致图象，
由图1可知，在有且仅有3个极大值点.故①正确；
②由图1、2可知，在有且仅有2个或3个极小值点.故②错误；

④当=sin（）=0时，=kπ（k∈Z），所以，
因为在上有5个零点，
所以当k=5时，，当k=6时，，解得，
故④正确.
③函数=sin（）的增区间为：，.
取k=0，
当时，单调递增区间为，
当时，单调递增区间为，
综上可得，在单调递增.故③正确.
所以结论正确的有①③④.故本题正确答案为D.
【名师点睛】本题为三角函数与零点结合问题，难度大，可数形结合，分析得出答案，要求高，理解深度高，考查数形结合思想．注意本题中极小值点个数是动态的，易错，正确性考查需认真计算，易出错．
5．【2019年高考天津卷理数】已知函数是奇函数，将的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为．若的最小正周期为，且，则（ ）
A． B．
C． D．
【答案】C
【解析】∵为奇函数，∴；
又∴，
又，∴，
∴，故选C.
【名师点睛】本题主要考查函数的性质和函数的求值问题，解题关键是求出函数，再根据函数性质逐步得出的值即可.
6. 【2018年高考天津理数】将函数的图象向右平移个单位长度，所得图象对应的函数（ ）
A．在区间上单调递增 B．在区间上单调递减
C．在区间上单调递增 D．在区间上单调递减
【答案】A
【解析】由函数图象平移变换的性质可知：将的图象向右平移个单位长度之后的解析式为.
则函数的单调递增区间满足，即，
令可得一个单调递增区间为.
函数的单调递减区间满足：，即，
令可得一个单调递减区间为：.
故选A.
【名师点睛】本题主要考查三角函数的平移变换，三角函数的单调区间的判断等知识，意在考查学生的转化能力和计算求解能力.
7. 【2018年高考浙江卷】函数y=sin2x的图象可能是（ ）
A． B．
C． D．
【答案】D
【解析】令，因为，所以为奇函数，排除选项A，B；
因为时，，所以排除选项C，
故选D.
【名师点睛】解答本题时，先研究函数的奇偶性，再研究函数在上的符号，即可作出判断.有关函数图象的识别问题的常见题型及解题思路：
（1）由函数的定义域，判断图象的左、右位置，由函数的值域，判断图象的上、下位置；
（2）由函数的单调性，判断图象的变化趋势；
（3）由函数的奇偶性，判断图象的对称性；
（4）由函数的周期性，判断图象的循环往复．
8.【2017年高考全国Ⅲ理数】设函数，则下列结论错误的是（ ）
A．的一个周期为
B．的图象关于直线对称
C．的一个零点为
D．在(，)单调递减
【答案】D
【解析】函数的最小正周期为，则函数的周期为，取，可得函数的一个周期为，选项A正确；
函数图象的对称轴为，即，取，可得y=f(x)的图象关于直线对称，选项B正确；
，函数的零点满足，即，取，可得的一个零点为，选项C正确；
当时，，函数在该区间内不单调，选项D错误.
故选D.
【名师点睛】（1）求最小正周期时可先把所给三角函数式化为或的形式，则最小正周期为；奇偶性的判断关键是解析式是否为或的形式.
（2）求的对称轴，只需令，求x；求f(x)的对称中心的横坐标，只需令即可.
【考法拓展•题型解码】
考法一　三角函数的图象及变换
归纳总结：三角函数图象的两种变换
(1)平移变换
①沿x轴平移：由y＝f(x)变为y＝f(x＋φ)时，“左加右减”，即φ>0，左移；φ0，上移；k0，ω>0)中参数的方法
(1)求A，b：确定函数的最大值M和最小值m，则A＝(M－m)/2，b＝(M＋m)/2.
(2)求ω：确定函数的周期T，则可得ω＝.
(3)求φ：常用的方法有：
①代入法：把图象上的一个已知点代入(此时A，ω，b已知)或代入图象与直线y＝b的交点求解(此时要注意交点是在上升区间还是在下降区间)．
②五点法：确定φ值时，往往以寻找“五点法”中的某一个点为突破口．具体如下：
“第一点”(即图象上升时与x轴的交点)为ωx＋φ＝0；“第二点”(即图象的“峰点”)为ωx＋φ＝；“第三点”(即图象下降时与x轴的交点)为ωx＋φ＝π；“第四点”(即图象的“谷点”)为ωx＋φ＝；“第五点”为ωx＋φ＝2π.
【例2】 (1)函数y＝Asin(ωx＋φ)的部分图象如图所示，则(　　)

A．y＝2sin B．y＝2sin
C．y＝2sin D．y＝2sin
【答案】A
【解析】由图象知A＝2，＝－＝，故T＝π，由此可排除C，D；将点依次代入选项A，B中的函数解析式，A项符合题意，B项不符合题意，由此排除选项B．故选A．
(2)如图是函数y＝Asin(ωx＋φ)＋b(A>0，ω>0)的图象的一部分，它的振幅、周期、初相各是(　　)

A．A＝3，T＝，φ＝－
B．A＝1，T＝，φ＝
C．A＝1，T＝，φ＝－
D．A＝1，T＝，φ＝－
【答案】C
【解析】由图象知，A＝＝1，b＝＝2，＝－＝，则T＝，ω＝.由×＋φ＝＋2kπ，k∈Z，得φ＝－＋2kπ，k∈Z，令k＝0，得φ＝－.
考法三　三角函数的单调性
解题技巧:三角函数单调性问题的常见类型及解题策略
(1)已知三角函数的解析式求单调区间：
①求函数的单调区间应遵循简单化原则，将解析式先化简，并注意复合函数单调性“同增异减”的规律；
②求形如y＝Asin(ωx＋φ)或y＝Acos(ωx＋φ)(其中ω>0)的单调区间时，要视“ωx＋φ”为一个整体，通过解不等式求解．但如果ω0，ω>0，φ∈R)，则“f(x)是奇函数”是“φ＝”的(　　)
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
【答案】B　
【解析】f(x)是奇函数时，φ＝＋kπ(k∈Z)；φ＝时，f(x)＝Acos＝－Asin ωx，为奇函数，所以“f(x)是奇函数”是“φ＝”的必要不充分条件
(2)(2018·江苏卷)已知函数y＝sin(2x＋φ)的图象关于直线x＝对称，则φ的值是__________．
【答案】　－
【解析】由2×＋φ＝kπ＋(k∈Z)得φ＝kπ－，又φ∈，取k＝0，φ＝－.
(3)设函数f(x)＝Asin(ωx＋φ)(A，ω，φ是常数，A>0，ω>0)．若f(x)在区间上具有单调性，且f ＝f ＝－f ，则f(x)的最小正周期为__________．
【答案】　π
【解析】记f(x)的最小正周期为T.由题意知≥－＝.又f ＝f ＝－f ，且－＝.
可作出示意图如图所示(一种情况)．

所以x1＝×＝，x2＝×＝，
所以＝x2－x1＝－＝.所以T＝π.
考法六　三角函数模型的应用
归纳总结
三角函数模型在实际中的应用体现在两个方面，一是已知函数模型，利用三角函数的有关性质解决问题，其关键是准确理解自变量的意义及自变量与函数之间的对应法则．二是把实际问题抽象转化成数学问题，建立三角函数模型，再利用三角函数的有关知识解决问题，其关键是建模．
【例7】 如图，某港口一天6时到18时的水深变化曲线近似满足函数y＝3sin＋k.据此函数可知，这段时间水深(单位：m)的最大值为(　　)

A．5 B．6
C．8 D．10
【答案】C　
【解析】 根据图象得函数的最小值为2，有－3＋k＝2，k＝5，最大值为3＋k＝8.
【易错警示】
易错点　图象变换出现错误
【典例】 要得到y＝sin的图象，只需将y＝sin的图象(　　)
A．向左平移个单位长度
B．向右平移个单位长度
C．向左平移个单位长度
D．向右平移个单位长度
【错解一】：由函数y＝sin的图象向左平移就得到y＝sin＝sin的图象．故选C．
【错解二】：由函数y＝sin的图象向右平移就得到y＝sin的图象．故选D．
【错因分析】：错解一中将y＝sin的图象向左平移得到的应该是函数y＝sin＝sin的图象，变换求式时忽视了x的系数－.
错解二对题意理解有误，是将谁平移变换得到谁弄反了，另外，若向右平移个单位，应该得到函数y＝sin＝sin的图象．
【正解答案】：B
【正解】：因为y＝sin＝sin，与y＝sin比较，只需x→x－即可．故选B．
【跟踪训练】 要得到函数y＝sin的图象，只需将函数y＝sin 4x的图象(　　)
A．向左平移个单位长度
B．向右平移个单位长度
C．向左平移个单位长度
D．向右平移个单位长度
【答案】B　
【解析】 由y＝sin＝sin 4得，只需将y＝sin 4x的图象向右平移个单位长度即可．故选B．
【递进题组】
1．把函数y＝sin的图象上所有点向右平移个单位长度，再将所得图象的横坐标变为原来的(纵坐标不变)，所得图象的解析式是y＝sin(ωx＋φ)(ω>0，|φ|