专题6.1 不等关系与不等式-2022年高考数学一轮复习核心素养大揭秘学案

这是一份专题6.1 不等关系与不等式-2022年高考数学一轮复习核心素养大揭秘学案，文件包含专题61不等关系与不等式解析版doc、专题61不等关系与不等式原卷版doc等2份学案配套教学资源，其中学案共21页， 欢迎下载使用。
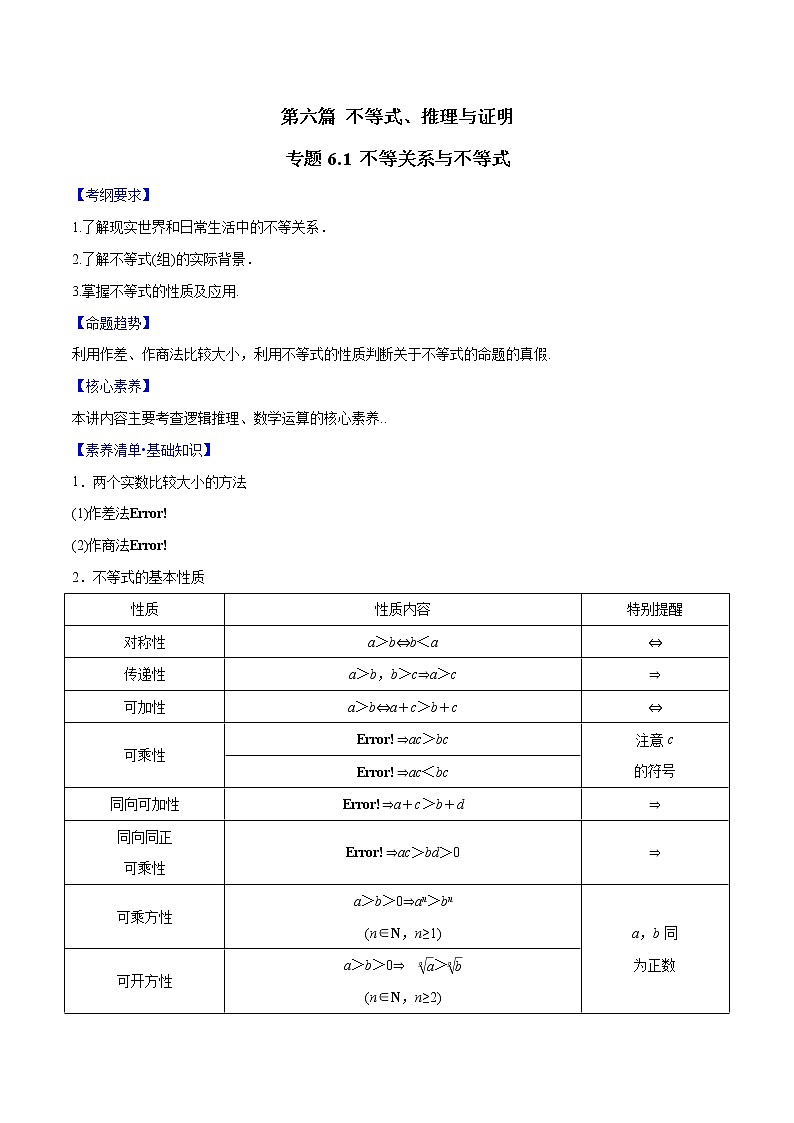
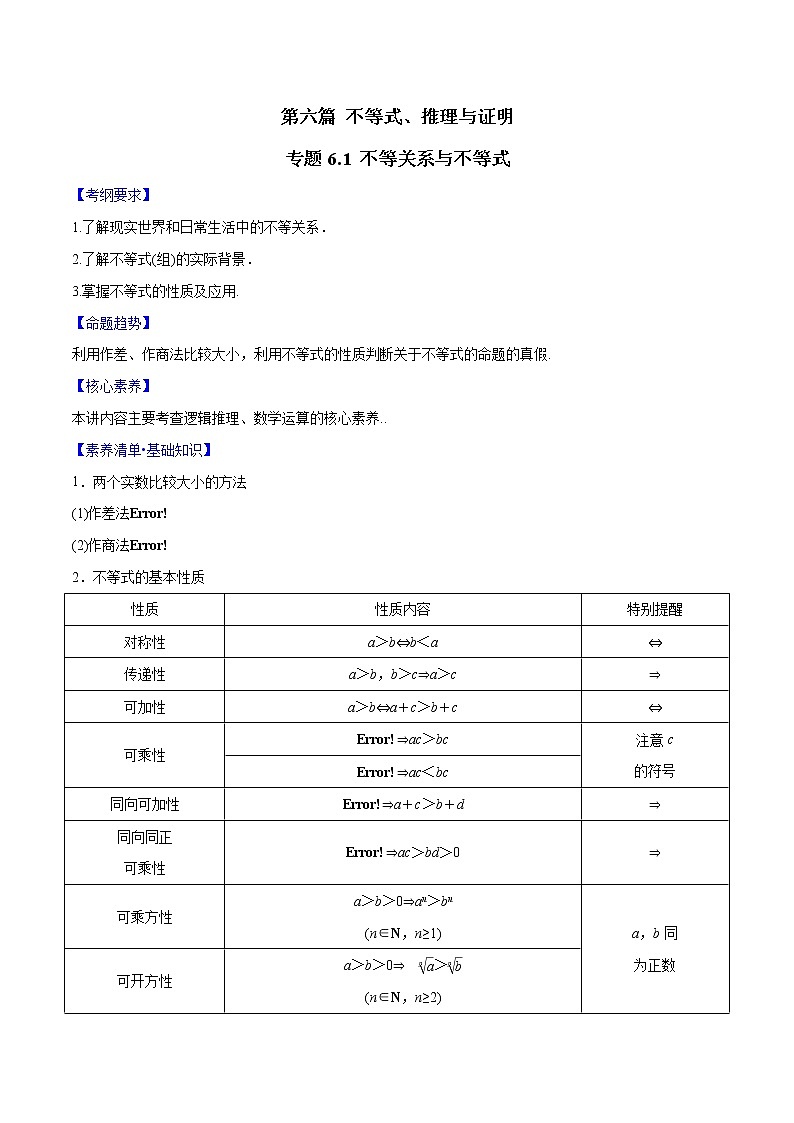
【考纲要求】
1.了解现实世界和日常生活中的不等关系．
2.了解不等式(组)的实际背景．
3.掌握不等式的性质及应用.
【命题趋势】
利用作差、作商法比较大小，利用不等式的性质判断关于不等式的命题的真假.
【核心素养】
本讲内容主要考查逻辑推理、数学运算的核心素养..
【素养清单•基础知识】
1．两个实数比较大小的方法
(1)作差法eq \b\lc\{\rc\ (\a\vs4\al\c1(a－b＞0⇔a ＞ ba，b∈R，,a－b＝0⇔a ＝ ba，b∈R，,a－b＜0⇔a ＜ ba，b∈R.))
(2)作商法eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(a,b)＞1⇔a ＞ ba∈R，b＞0，,\f(a,b)＝1⇔a ＝ ba∈R，b＞0，,\f(a,b)＜1⇔a ＜ ba∈R，b＞0.))
2．不等式的基本性质
3.不等式的一些常用性质
(1)倒数的性质
①a＞b，ab＞0⇒eq \f(1,a)＜eq \f(1,b)；
②a＜0＜b⇒eq \f(1,a)＜eq \f(1,b)；
③a＞b＞0，d>c>0⇒eq \f(a,c)＞eq \f(b,d)；
④0＜a＜x＜b或a＜x＜b＜0⇒eq \f(1,b)＜eq \f(1,x)＜eq \f(1,a).
(2)有关分数的性质
若a＞b＞0，m＞0，则：
①eq \f(b,a)＜eq \f(b＋m,a＋m)，eq \f(b,a)＞eq \f(b－m,a－m)(b－m＞0)；
②eq \f(a,b)＞eq \f(a＋m,b＋m)，eq \f(a,b)＜eq \f(a－m,b－m)(b－m＞0)．
【真题体验】
1.【2019年高考全国II卷理数】若a>b，则（ ）
A．ln(a−b)>0 B．3a0 D．│a│>│b│
2.【2019年高考全国I卷理数】古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是（≈0.618，称为黄金分割比例)，著名的“断臂维纳斯”便是如此．此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是．若某人满足上述两个黄金分割比例，且腿长为105 cm，头顶至脖子下端的长度为26 cm，则其身高可能是（ ）
A．165 cmB．175 cm
C．185 cmD．190 cm
3.【2018年高考全国III卷理数】设，，则（ ）
A． B．
C． D．
4.【2017年高考山东卷理数】若，且，则下列不等式成立的是（ ）
A． B．
C． D．
5.【2017年高考北京卷理数】能够说明“设a，b，c是任意实数．若a＞b＞c，则a+b＞c”是假命题的一组整数a，b，c的值依次为___________.
【考法解码•题型拓展】
考法一 比较两个数(式)的大小
解题技巧： 比较大小的常用方法
(1)作差法：其基本步骤为作差、变形、判断符号、得出结论．用作差法比较大小的关键是判断差的正负，常采用配方、因式分解、分子(分母)有理化等变形方法．
(2)作商法：即判断商与1的关系，得出结论．要特别注意当商与1的大小确定后必须对商式分子分母的正负进行判断，这是用作商法比较大小时最容易漏掉的关键步骤．
(3)单调性法：利用有关函数的单调性比较大小．
(4)特殊值验证法：对于一些题目，有的给出取值范围，可采用特殊值验证法比较大小．
【例1】 (1)已知a1，a2∈(0,1)，记M＝a1a2，N＝a1＋a2－1，则M与N的大小关系是( )
A．M＜N B．M＞N
C．M＝N D．不确定
(2)对于0＜a＜1，给出下列四个不等式：
①lga(1＋a)＜lgaeq \b\lc\(\rc\)(\a\vs4\al\c1(1＋\f(1,a)))；
②lga(1＋a)＞lgaeq \b\lc\(\rc\)(\a\vs4\al\c1(1＋\f(1,a)))；
③a1＋a＜a1＋eq \s\up10(\f(1,a))；
④a1＋a＞a1＋eq \s\up10(\f(1,a)).
其中成立的是( )
A．①③ B．①④
C．②③ D．②④
(3)若a＝eq \f(ln 3,3)，b＝eq \f(ln 4,4)，c＝eq \f(ln 5,5)，则( )
A．a＜b＜c B．c＜b＜a
C．c＜a＜b D．b＜a＜c
考法二 不等式的性质及简单应用
归纳总结
(1)判断不等式是否成立，需要逐一给出推理判断或反例说明．常用的推理判断需要利用不等式的性质．
(2)在判断一个关于不等式的命题真假时，先把要判断的命题和不等式性质联系起来考虑，找到与命题相近的性质，并应用性质判断命题真假，当然判断的同时还要用到其他知识，比如对数函数、指数函数的性质等．
(3)解决与充分、必要条件相结合的问题时，先用不等式的性质分别判断p⇒q和q⇒p是否正确，再得出结论，要注意特殊值法的应用．
【例2】 (1)已知a，b，c，d为实数，则“a＞b且c>d”是“ac＋bd＞bc＋ad”的( )
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
(2)若eq \f(1,a)＜eq \f(1,b)＜0，则下列不等式：①a＋b＜ab；②eq \b\lc\|\rc\|(\a\vs4\al\c1(a))＞eq \b\lc\|\rc\|(\a\vs4\al\c1(b))；③a＜b；④ab＜b2中，正确的不等式有( )
A．①② B．②③
C．①④ D．③④
考法三 应用不等式的性质求范围
误区防范：应用不等式性质求范围问题的注意点
应用不等式的性质求某些代数式的取值范围应注意两点：一是必须严格运用不等式的性质；二是在多次运用不等式的性质时有可能扩大了变量的取值范围．解决的途径是先建立所求范围的整体与已知范围的整体的等量关系，最后通过“一次性”不等关系的运算求解范围．此外，这类问题还可以用线性规划的知识求解．
【例3】 三个正数a，b，c满足a≤b＋c≤2a，b≤a＋c≤2b，则eq \f(b,a)的取值范围是__________．
【易错警示】
易错点 忽视参数之间的制约关系，扩大了范围
【典例】 已知函数f(x)＝ax2－c，－4≤f(1)≤－1，－1≤f(2)≤5，求f(3)的取值范围．
【错解】：由题意可知eq \b\lc\{\rc\ (\a\vs4\al\c1(－4≤a－c≤－1，,－1≤4a－c≤5，))由不等式的性质可知eq \b\lc\{\rc\ (\a\vs4\al\c1(0≤a≤3，,1≤c≤7，))故eq \b\lc\{\rc\ (\a\vs4\al\c1(0≤9a≤27，,－7≤－c≤－1，))因此－7≤f(3)≤26.
【错因分析】：由eq \b\lc\{\rc\ (\a\vs4\al\c1(－4≤a－c≤－1，,－1≤4a－c≤5，))得到a，c自身的取值范围是正确的，但事实上，a，c之间还存在着相互制约的关系，错解中忽略了这种制约关系，从而将f(3)的范围扩大了．
【正解】：设f(3)＝mf(1)＋nf(2)，则9a－c＝m(a－c)＋n(4a－c)，即9a－c＝(m＋4n)a－(m＋n)c，比较a，c的系数可知eq \b\lc\{\rc\ (\a\vs4\al\c1(m＋4n＝9，,m＋n＝1，))所以eq \b\lc\{\rc\ (\a\vs4\al\c1(m＝－\f(5,3)，,n＝\f(8,3)，))即f(3)＝－eq \f(5,3)f(1)＋eq \f(8,3)f(2)．
又－4≤f(1)≤－1，所以eq \f(5,3)≤－eq \f(5,3)f(1)≤eq \f(20,3)；
－1≤f(2)≤5，所以－eq \f(8,3)≤eq \f(8,3)f(2)≤eq \f(40,3).
所以－1≤－eq \f(5,3)f(1)＋eq \f(8,3)f(2)≤20，即－1≤f(3)≤20.
【误区防范】：求代数式的取值范围的问题
由a＜f(x，y)＜b，c＜g(x，y)＜d求F(x，y)的取值范围，可利用待定系数法解决，设F(x，y)＝mf(x，y)＋ng(x，y)，用恒等变形求得m，n，再利用不等式的性质求得F(x，y)的取值范围．
【跟踪训练】 已知－1＜x＋y＜4且2＜x－y＜3，则z＝2x－3y的取值范围__________．(答案用区间表示)
【递进题组】
1．若f(x)＝3x2－x＋1，g(x)＝2x2＋x－1，则f(x)，g(x)的大小关系是( )
A．f(x)＝g(x)
B．f(x)＞g(x)
C．f(x)＜g(x)
D．随x值的变化而变化
2．若a，b∈R且a＞b，则下列不等式恒成立的是( )
A．a2＞b2 B. eq \f(a,b)＞1
C．2a＞2b D．lg(a－b)＞0
3．已知a，b，c∈R，那么下列命题中正确的是( )
A．若a＞b，则ac2＞bc2
B．若eq \f(a,c)＞eq \f(b,c)，则a＞b
C．若a3＞b3且ab＜0，则eq \f(1,a)＞eq \f(1,b)
D．若a2＞b2且ab＞0，则eq \f(1,a)＜eq \f(1,b)
4．已知△ABC的三边长分别为a，b，c，且满足b＋c≤3a，则eq \f(c,a)的取值范围为( )
A．(1，＋∞) B．(0,2)
C．(1,3) D．(0,3)
【考卷送检】
一、选择题
1．设a，b为实数，则“a