专题7.4 直线、平面垂直的判定及性质-2022年高考数学一轮复习核心素养大揭秘学案

这是一份专题7.4 直线、平面垂直的判定及性质-2022年高考数学一轮复习核心素养大揭秘学案，文件包含专题704直线平面垂直的判定及性质解析版doc、专题704直线平面垂直的判定及性质原卷版doc等2份学案配套教学资源，其中学案共38页， 欢迎下载使用。
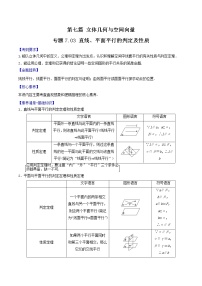
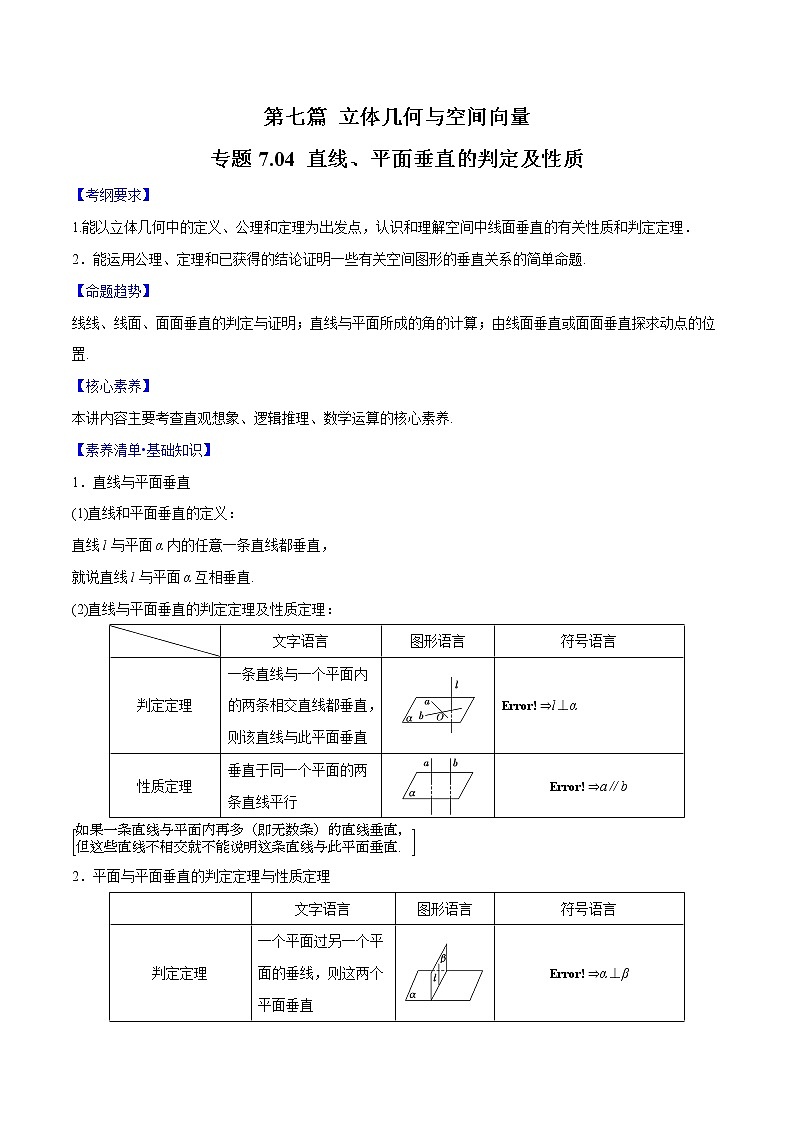
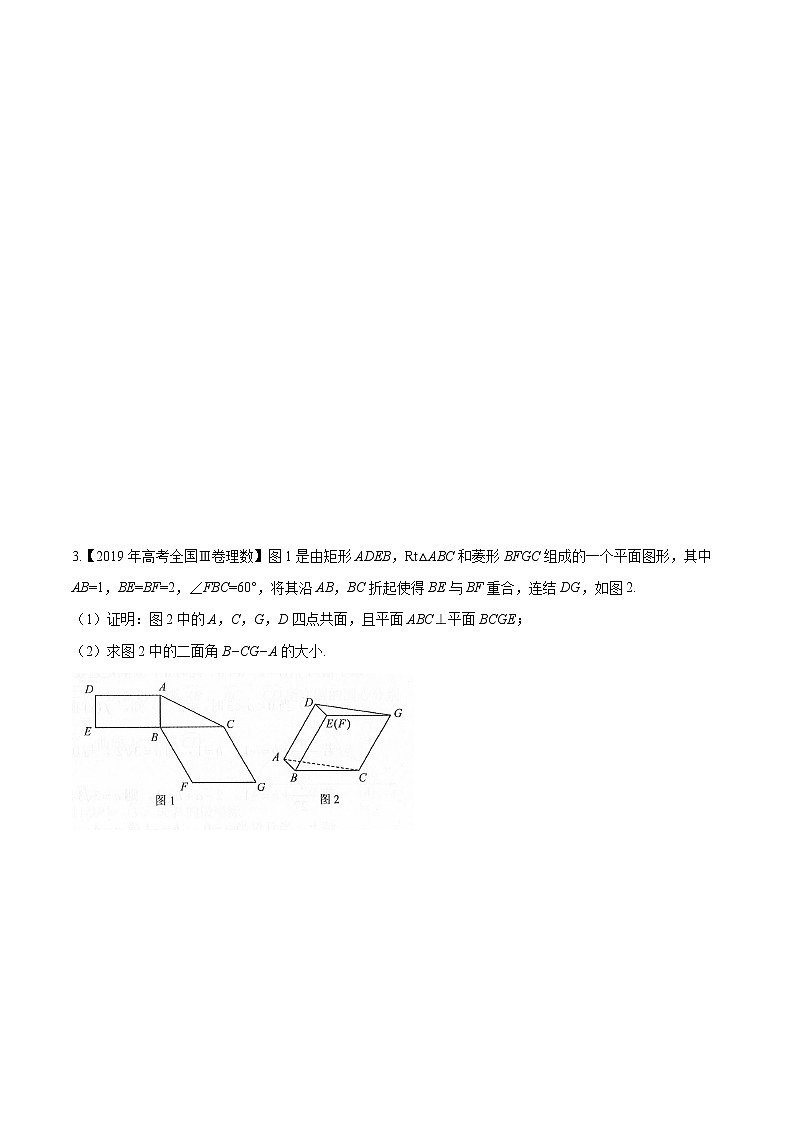
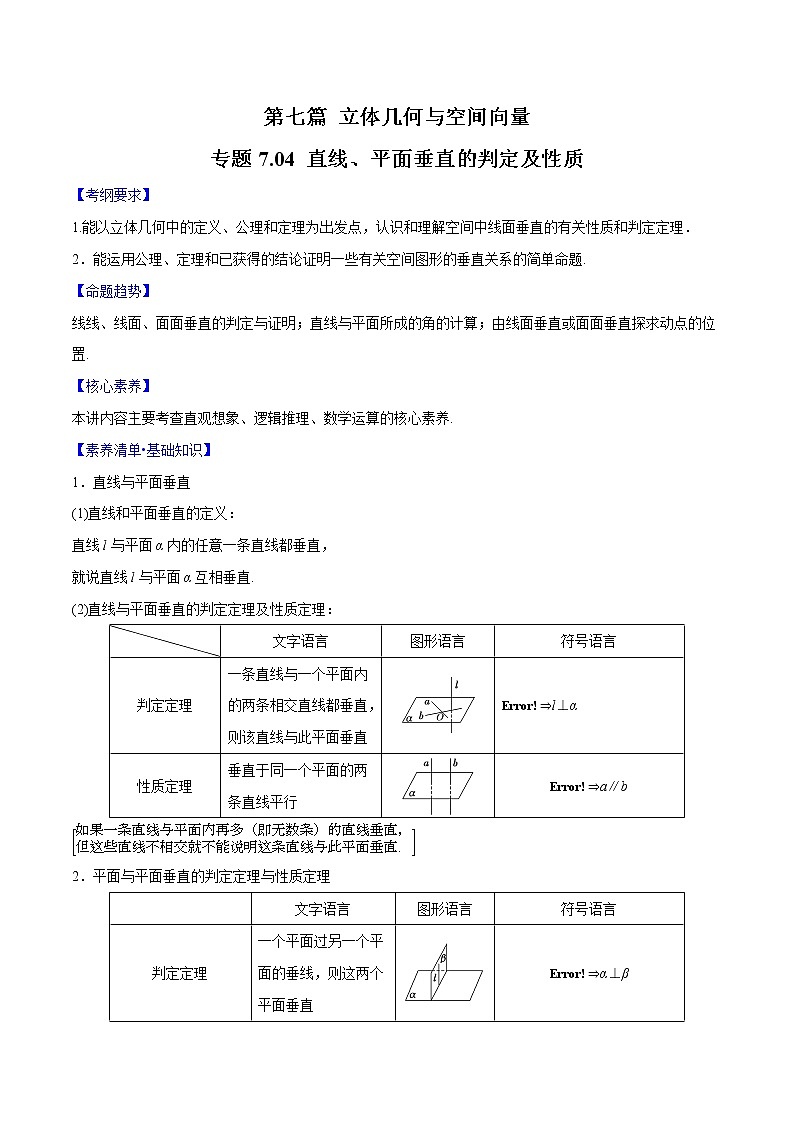
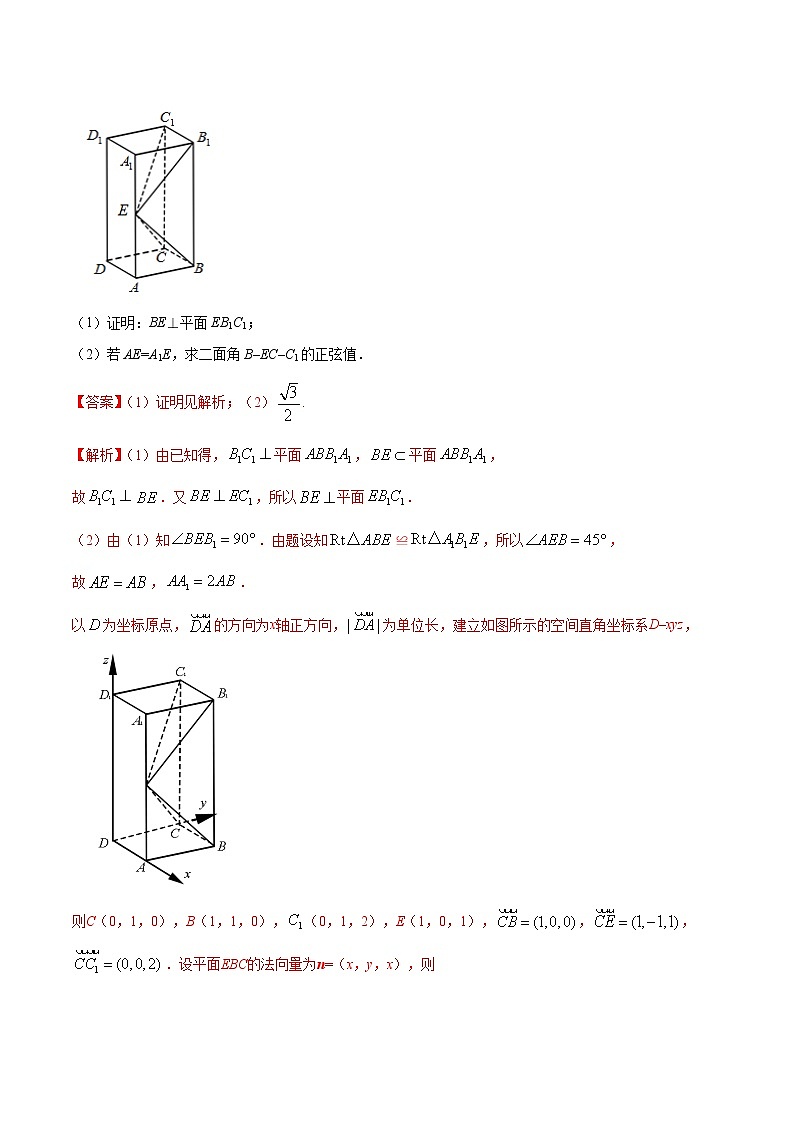
第七篇 立体几何与空间向量专题7.04 直线、平面垂直的判定及性质【考纲要求】1.能以立体几何中的定义、公理和定理为出发点，认识和理解空间中线面垂直的有关性质和判定定理．2．能运用公理、定理和已获得的结论证明一些有关空间图形的垂直关系的简单命题.【命题趋势】线线、线面、面面垂直的判定与证明；直线与平面所成的角的计算；由线面垂直或面面垂直探求动点的位置.【核心素养】本讲内容主要考查直观想象、逻辑推理、数学运算的核心素养.【素养清单•基础知识】1．直线与平面垂直(1)直线和平面垂直的定义：直线l与平面α内的任意一条直线都垂直，就说直线l与平面α互相垂直. (2)直线与平面垂直的判定定理及性质定理： 文字语言图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直⇒l⊥α性质定理垂直于同一个平面的两条直线平行⇒a∥b2．平面与平面垂直的判定定理与性质定理 文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线，则这两个平面垂直⇒α⊥β性质定理两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直⇒l⊥α[要求一平面只需过另一平面的垂线．]【素养清单•常用结论】直线与平面垂直的五个结论(1)若一条直线垂直于一个平面，则这条直线垂直于这个平面内的任意直线．(2)若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．(3)垂直于同一条直线的两个平面平行．(4)一条直线垂直于两平行平面中的一个，则这一条直线与另一个平面也垂直．(5)两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面．【真题体验】1.【2019年高考北京卷理数】已知l，m是平面外的两条不同直线．给出下列三个论断：①l⊥m；②m∥；③l⊥．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________． 2.【2019年高考全国Ⅱ卷理数】如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1．（1）证明：BE⊥平面EB1C1；（2）若AE=A1E，求二面角B–EC–C1的正弦值．               3.【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连结DG，如图2.（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的二面角B−CG−A的大小.      4.【2019年高考北京卷理数】如图，在四棱锥P–ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3．E为PD的中点，点F在PC上，且．（1）求证：CD⊥平面PAD；（2）求二面角F–AE–P的余弦值；（3）设点G在PB上，且．判断直线AG是否在平面AEF内，说明理由．      5.【2019年高考浙江卷】如图，已知三棱柱，平面平面,，分别是AC，A1B1的中点.（1）证明：；（2）求直线EF与平面A1BC所成角的余弦值.              【考法拓展•题型解码】考法一　　直线与平面垂直的判定与性质归纳总结　　 　　　　　　　　　　　　　　　　　(1)判断直线和平面垂直的常用方法：①判定定理；②若两条平行直线中的一条垂直于一个平面，则另一条也垂直于这个平面；③若一条直线垂直于两个平行平面中的一个平面，则它必垂直于另一个平面；④若两平面垂直，则在一个平面内垂直于交线的直线必垂直于另一个平面；⑤若两相交平面同时垂直于第三个平面，则这两个平面的交线垂直于第三个平面．其中②③⑤是客观题中常用的方法．(2)证明线面垂直的核心是证线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想．(3)线面垂直的性质常用来证明线线垂直．【例1】 (2018·浙江卷)如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC＝120°，A1A＝4，C1C＝1，AB＝BC＝B1B＝2.(1)证明：AB1⊥平面A1B1C1；(2)求直线AC1与平面ABB1所成的角的正弦值．          考法二　　平面与平面垂直的判定与性质归纳总结：(1)判定面面垂直的方法：①面面垂直的定义；②面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β)．(2)在已知平面垂直时，一般要用性质定理进行转化．在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．【例2】 (2017·全国卷Ⅰ)如图，在四棱锥PABCD中，AB∥CD，且∠BAP＝∠CDP＝90°.(1)证明：平面PAB⊥平面PAD；(2)若PA＝PD＝AB＝DC，∠APD＝90°，且四棱锥PABCD的体积为，求该四棱锥的侧面积．         考法三　　垂直关系中的探索性问题解题技巧：解决垂直关系中的探索性问题的途径(1)先猜后证，即先观察与尝试给出条件再证明．(2)先通过命题成立的必要条件探索出命题成立的条件，再证明充分性．(3)将几何问题转化为代数问题，探索出命题成立的条件．【例3】 如图，正方形ABCD的边长为2，PA⊥平面ABCD，PA＝2，平面EBC⊥平面ABCD，EB＝EC＝.(1)在CD上是否存在一点F，使得BF⊥平面PAE？若存在，确定点F的位置；若不存在，请说明理由．(2)求多面体PABCDE的体积．            【规范解答】关键点　平行垂直关系的综合应用【典例】 (2017·全国卷Ⅱ)如图，四棱锥PABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB＝BC＝AD，∠BAD＝∠ABC＝90°.(1)证明：直线BC∥平面PAD；(2)若△PCD的面积为2，求四棱锥P－ABCD的体积．【答案】见解析【解析】(1)证明：在平面ABCD中，因为∠BAD＝∠ABC＝90°.所以BC∥AD，又BC⊄平面PAD，AD⊂平面PAD.所以直线BC∥平面PAD.(2)如图，取AD的中点M，连接PM，CM，由AB＝BC＝AD及BC∥AD，∠ABC＝90°得四边形ABCM为正方形，则CM⊥AD.因为侧面PAD为等边三角形且垂直于底面ABCD，平面PAD∩平面ABCD＝AD，PM⊂平面PAD，所以PM⊥AD，PM⊥底面ABCD，因为CM⊂底面ABCD，所以PM⊥CM.设BC＝x，则CM＝x，CD＝x，PM＝x，PC＝PD＝2x，如图，取CD的中点N，连接PN，则PN⊥CD，所以PN＝x.因为△PCD的面积为2，所以×x×x＝2，解得x＝－2(舍去)或x＝2.于是AB＝BC＝2，AD＝4，PM＝2.所以四棱锥P－ABCD的体积V＝××2＝4.答题模板　　 　　　　　　　　　　　　　　　　　第一步：根据平面几何性质，证BC∥AD.第二步：由线面平行判定定理，证BC∥平面PAD.第三步：判定四边形ABCM为正方形，得CM⊥AD.第四步：证明直线PM⊥平面ABCD.第五步：利用面积求边BC，并计算相关量．第六步：计算四棱锥P－ABCD的体积．【跟踪训练】 如图，在四边形ABCD中，AB∥CD，BC＝CD＝DA＝AB＝2，点E为AB的中点，以DE为折痕将△ADE折起，使点A到达点P的位置，平面PDE⊥平面BCDE，点F为PB的中点．(1)求证：PD∥平面CEF；(2)求三棱锥P－DEF的体积．【答案】见解析【解析】(1)证明：因为点E为AB的中点，AB∥CD，AB＝2CD，所以BE＝CD且BE∥CD，所以四边形BCDE是平行四边形．连接BD交CE于点O，则点O为BD的中点，连接FO，因为点F为PB的中点，所以PD∥FO，又PD⊄平面CEF，FO⊂平面CEF，所以PD∥平面CEF.(2)由(1)可知，PD∥FO，FO⊄平面PDE，所以FO∥平面PDE，所以点F到平面PDE的距离与点O到平面PDE的距离相等．连接OP，则VP－DEF＝VF－PDE＝VO－PDE＝VP－ODE.由题意及四边形BCDE是平行四边形得BC＝CD＝PD＝PE＝BE＝DE＝2，取DE的中点H，连接PH，则PH⊥DE，且PH＝.因为平面PDE⊥平面BCDE，平面PDE∩平面BCDE＝DE，PH⊂平面PDE，所以PH⊥平面BCDE.由题意得四边形ABCD为等腰梯形且∠ABC＝60°，又四边形BCDE为菱形，所以∠EDC＝60°，所以S△ODE＝S△DEC＝××2×2×sin 60°＝，所以VP－DEF＝VP－ODE＝·S△ODE×PH＝××＝.【递进题组】1．设m，n是两条不同的直线，α，β是两个不同的平面则下列说法正确的是(　　)A．若m⊥n，n∥α，则m⊥αB．若m∥β，β⊥α，则m⊥αC．若m⊥β，n⊥β，n⊥α，则m⊥αD．若m⊥n，n⊥β，β⊥α，则m⊥α2．(2019·天津模拟)设l是直线，α，β是两个不同的平面，则下列说法正确的是(　　)A．若l∥α，l∥β，则α∥βB．若l∥α，l⊥β，则α⊥βC．若α⊥β，l⊥α，则l∥βD．若α⊥β，l∥α，则l⊥β3．如图，在四棱锥PABCD中，PA⊥底面ABCD，AB⊥AD, AC⊥CD，∠ABC＝60°， PA＝AB＝BC，E是PC的中点．证明：(1) CD⊥AE；(2)PD⊥平面ABE.           4．如图，在四棱锥SABCD中，平面SAD⊥平面ABCD，四边形ABCD为正方形，且P为AD的中点．(1)求证：CD⊥平面SAD；(2)若SA＝SD，M为BC的中点，在棱SC上是否存在点N，使得平面DMN⊥平面ABCD？并证明你的结论．     【考卷送检】 一、选择题1．若α，β表示两个不同的平面，直线m⊂α，则“α⊥β”是“m⊥β”的(　　)A．充分不必要条件                   B．必要不充分条件C．充要条件                         D．既不充分也不必要条件2．已知平面α⊥平面β，α∩β＝l，点A∈α，A∉l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是　(　　)A．AB∥m                               B．AC⊥mC．AB∥β                               D．AC⊥β3．(2019·忻州二中月考)设m，n是两条不同的直线，α，β，γ是三个不同的平面．下列命题中正确的有(　　)①若m⊂β，α⊥β，则m⊥α；②若α∥β，m⊂α，则m∥β；③若n⊥α，n⊥β，m⊥α，则m⊥β；④若α⊥γ，β⊥γ，则α⊥β.A．①③                                    B．①②C．③④                                    D．②③4．如图，在斜三棱柱ABCA1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在(　　)A．直线AB上B．直线BC上C．直线AC上D．△ABC内部5．如图，在四边形ABCD 中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD，构成三棱锥ABCD，则在三棱锥 A－BCD中，下列命题正确的是(　　)A．平面ABD⊥平面ABCB．平面ADC⊥平面BDCC．平面ABC⊥平面BDCD．平面ADC⊥平面ABC6．(2019·宝鸡质检)对于四面体ABCD，给出下列四个命题：①若AB＝AC，BD＝CD，则BC⊥AD；②若AB＝CD，AC＝BD，则BC⊥AD；③若AB⊥AC，BD⊥CD，则BC⊥AD；④若AB⊥CD，AC⊥BD，则BC⊥AD.其中为真命题的是(　　)A．①②                              B．②③C．②④                              D．①④二、填空题7．如图，已知PA⊥平面ABC，BC⊥AC，则图中直角三角形的个数为________．8．(2019·合肥三中月考)已知a，b表示两条不同的直线，α，β，γ表示三个不同的平面，给出下列命题：①若α∩β＝a，b⊂α，a⊥b，则α⊥β；②若a⊂α，a垂直于β内的任意一条直线，则α⊥β；③若α⊥β，α∩β＝a，α∩γ＝b，则a⊥b；④若a不垂直于平面α，则a不可能垂直于平面α内的无数条直线；⑤若a⊥α，a⊥β，则α∥β.其中正确命题的序号是________．9．如图，在直四棱柱ABCDA1B1C1D1中，∠ADC＝90°，且AA1＝AD＝DC＝2，M∈平面ABCD，当D1M⊥平面A1C1D时，DM＝________.三、解答题10．如图，在四棱柱ABCDA1B1C1D1中，侧面ADD1A1和侧面CDD1C1都是矩形，BC∥AD，△ABD是正三角形，E，F分别为AD，A1D1的中点．(1)求证：DD1⊥平面ABCD；(2)求证：平面A1BE⊥平面ADD1A1.         11．(2019·渭南检测)如图所示，在四棱锥P－ABCD中，底面ABCD是矩形，且AD＝2，AB＝1，PA⊥平面ABCD，E，F分别是线段AB，BC的中点．(1)证明：PF⊥FD；(2)若PA＝1，求点E到平面PFD的距离．          12．(2016·浙江卷)如图，在三棱台ABC－DEF中，平面 BCFE⊥平面ABC，∠ACB＝90°，BE＝EF＝FC＝1，BC＝2，AC＝3.　(1)求证：BF⊥平面ACFD；(2)求直线BD与平面ACFD所成角的余弦值．            13．如图所示，在直角梯形ABCD 中，BC⊥DC，AE⊥DC，N，M分别是AD，BE的中点， 将三角形ADE沿AE折起，下列说法正确的是________(填上所有正确说法的序号)．①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC；②不论D折至何位置都有MN⊥AE；③不论D折至何位置(不在平面ABC内)都有MN∥AB.