



所属成套资源:2022年高考数学一轮复习核心素养大揭秘
专题10.4 变量间的相关关系与统计案例-2022年高考数学一轮复习核心素养大揭秘学案
展开
这是一份专题10.4 变量间的相关关系与统计案例-2022年高考数学一轮复习核心素养大揭秘学案,文件包含专题104变量间的相关关系与统计案例解析版doc、专题104变量间的相关关系与统计案例原卷版doc等2份学案配套教学资源,其中学案共31页, 欢迎下载使用。
【考纲要求】
1.会作两个有关联变量的数据的散点图,并利用散点图认识变量间的相关关系.
2.了解最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程.
3.了解常见的统计方法,了解回归分析的基本思想并能应用这些方法解决一些实际问题.
4.了解独立性检验(只要求2×2列联表)的基本思想、方法及其简单应用.
【命题趋势】
1.散点图与相关关系、线性回归方程与独立性检验在实际生活中的应用.
2.有关统计内容及方法主要以选择题、填空题的形式呈现,属容易题;抽样方法和各种统计图表与概率的有关内容相结合或与统计案例相结合也会出现在解答题中,属中档题.
【核心素养】
本讲内容突出对数据分析,数学运算核心素养的考查.
【素养清单•基础知识】
1.相关关系与回归方程
(1)相关关系的分类
①正相关:从散点图上看,点散布在从左下角到右上角的区域内.
②负相关:从散点图上看,点散布在从左上角到右下角的区域内.
(2)线性相关关系
从散点图上看,如果这些点从整体上看大致分布在一条直线附近,则称这两个变量之间具有线性相关关系,这条直线叫回归直线.
(3)回归方程
①最小二乘法:使得样本数据的点到回归直线的距离的平方和最小的方法叫最小二乘法.
②回归方程:两个具有线性相关关系的变量的一组数据为(x1,y1),(x2,y2),…,(xn,yn),其回归方程为,其中eq \(b,\s\up18(^))=eq \f(\i\su(i=1,n, )x i-\x\t(x)yi-\x\t(y),\i\su(i=1,n, )x i-\x\t(x)2),eq \(a,\s\up18(^))=eq \x\t(y)-eq \(b,\s\up18(^)) eq \x\t(x).
(eq \x\t(x),eq \x\t(y))称为样本点的中心.
(4)样本相关系数r=eq \f(\i\su(i=1,n, )x i-\x\t(x)yi-\x\t(y),\r(\i\su(i=1,n, )x i-\x\t(x)2\i\su(i=1,n, )yi-\x\t(y)2)),用它来衡量两个变量间的线性相关关系的强弱.
①当r>0时,表明两个变量正相关;
②当r<0时,表明两个变量负相关;
③r的绝对值越接近1,表明两个变量的线性相关性越强;r的绝对值越接近0,表明两个变量的线性相关性越弱,通常当eq \b\lc\|\rc\|(\a\vs4\al\c1(r))>0.75时,认为两个变量有很强的线性相关关系.
2.独立性检验
(1)分类变量:变量的不同“值”表示个体所属的不同类别,像这类变量称为分类变量.
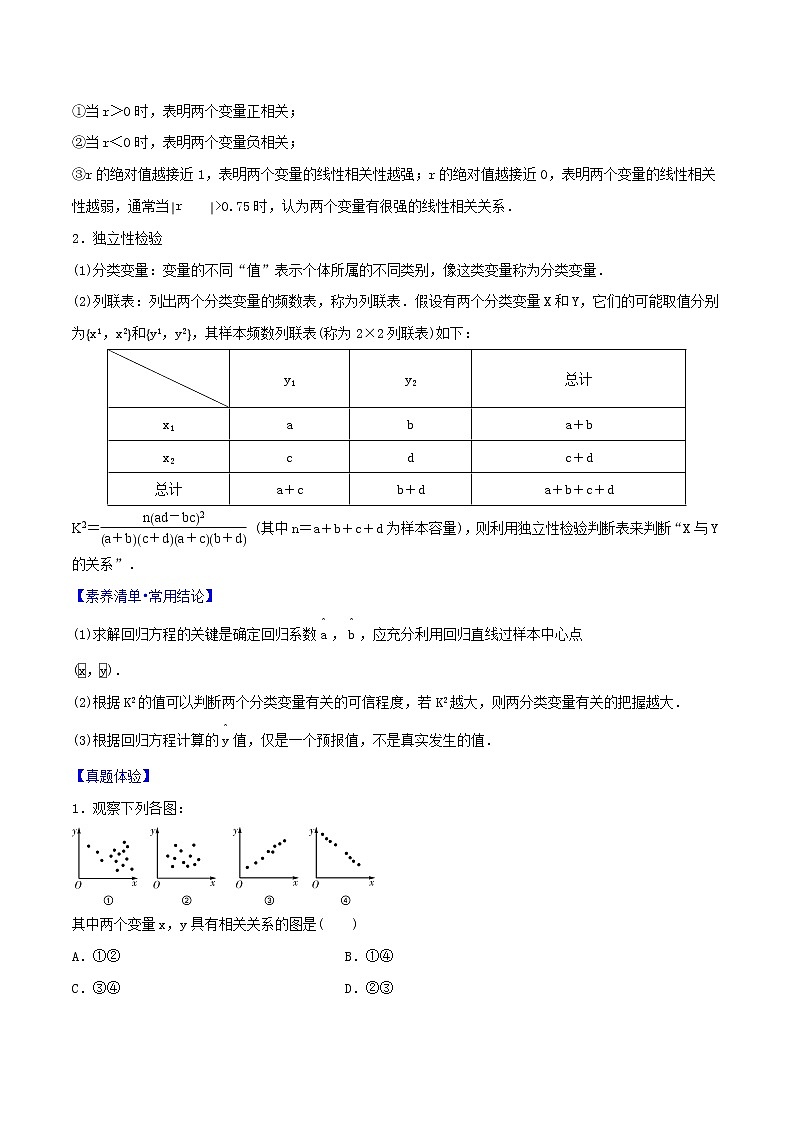
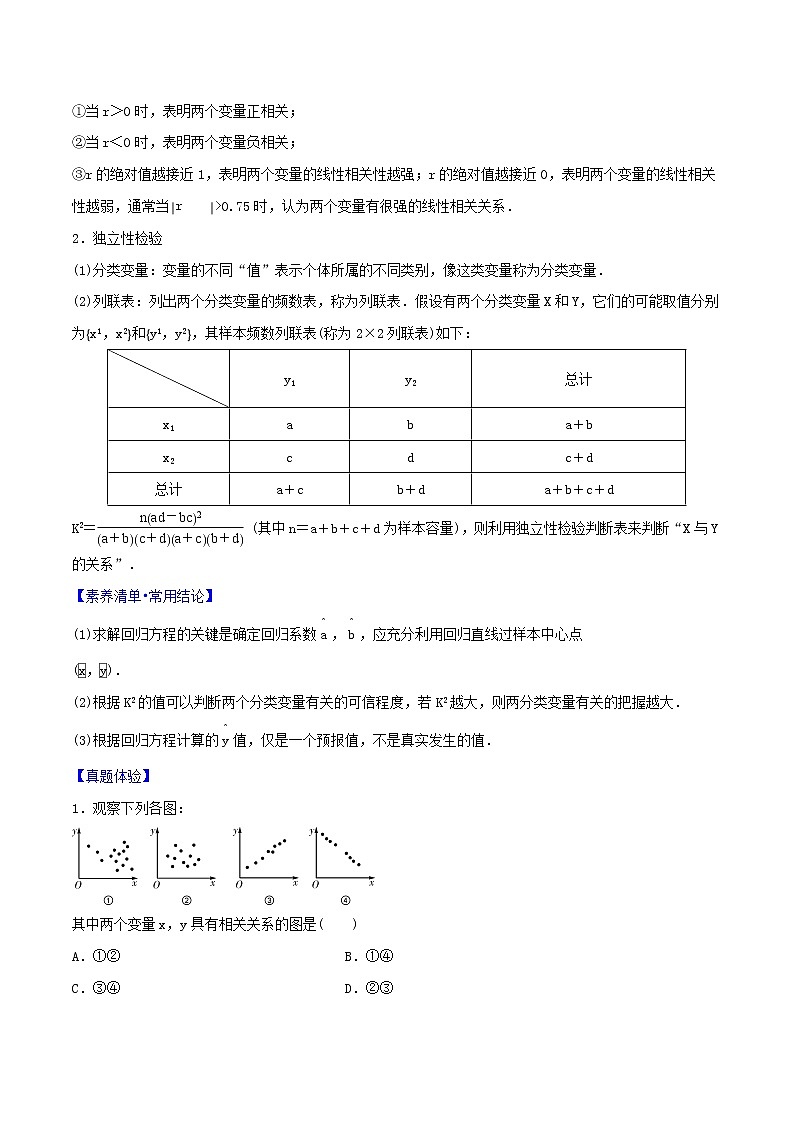
(2)列联表:列出两个分类变量的频数表,称为列联表.假设有两个分类变量X和Y,它们的可能取值分别为eq \b\lc\{\rc\}(\a\vs4\al\c1(x1,x2))和eq \b\lc\{\rc\}(\a\vs4\al\c1(y1,y2)),其样本频数列联表(称为2×2列联表)如下:
K2=eq \f(nad-bc2,a+bc+da+cb+d) (其中n=a+b+c+d为样本容量),则利用独立性检验判断表来判断“X与Y的关系”.
【素养清单•常用结论】
(1)求解回归方程的关键是确定回归系数eq \(a,\s\up6(^)),eq \(b,\s\up6(^)),应充分利用回归直线过样本中心点
(eq \x\t(x),eq \x\t(y)).
(2)根据K2的值可以判断两个分类变量有关的可信程度,若K2越大,则两分类变量有关的把握越大.
(3)根据回归方程计算的eq \(y,\s\up6(^))值,仅是一个预报值,不是真实发生的值.
【真题体验】
1.观察下列各图:
其中两个变量x,y具有相关关系的图是( )
A.①② B.①④
C.③④ D.②③
【答案】C
【解析】由散点图知③④具有相关关系.
2.已知x,y的取值如下表,从散点图可以看出y与x线性相关,且回归方程为eq \(y,\s\up18(^))=0.95x+eq \(a,\s\up18(^)),则eq \(a,\s\up18(^))=( )
B.2.6
C.2.2 D.0
【答案】B
【解析】由已知得eq \(x,\s\up18(-))=2,eq \(y,\s\up18(-))=4.5,因为回归方程经过点(eq \(x,\s\up18(-)),eq \(y,\s\up18(-))),所以=4.5-0.95×2=2.6.
3.若回归直线方程为eq \(y,\s\up18(^))=2-1.5x,则变量x增加一个单位,y( )
A.平均增加1.5个单位
B.平均增加2个单位
C.平均减少1.5个单位
D.平均减少2个单位
【答案】C
【解析】因为回归直线方程为 =2-1.5x,所以=-1.5,则变量x增加一个单位,y平均减少1.5个单位.
4.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是 ( )
A.若K2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病
B.从独立性检验可知,有99%的把握认为吸烟与患肺病有关时,我们说某人吸烟,那么他有99%的可能患有肺病
C.若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误
D.以上三种说法都不正确
【答案】C
【解析】根据独立性检验的思想知C项正确.
【考法拓展•题型解码】
考法一 相关关系的判断
归纳总结
判定两个变量正、负相关性的方法
(1)画散点图:点的分布从左下角到右上角,两个变量正相关;点的分布从左上角到右下角,两个变量负相关.
(2)相关系数:r>0时,正相关;r0时,正相关;eq \(b,\s\up18(^))3.841时,有1-0.05=0.95的几率,也就是有95%的把握认为变量之间有关系,故选D.
4.(2019·大连双基测试)对于下列表格所示五个散点,已知求得的线性回归方程为eq \(y,\s\up18(^))=0.8x-155,则实数m的值为( )
A.8 B.8.2
C.8.4 D.8.5
【答案】A
【解析】eq \x\t(x)=eq \f(196+197+200+203+204,5)=200,eq \x\t(y)=eq \f(1+3+6+7+m,5)=eq \f(17+m,5),将样本中心点eq \b\lc\(\rc\)(\a\vs4\al\c1(200,\f(17+m,5)))代入=0.8x-155,可得m=8,故选A.
5.如表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据,根据表提供的数据,求出y关于x的线性回归方程为eq \(y,\s\up18(^))=0.7x+0.35,则下列结论错误的是( )
A.产品的生产能耗与产量呈正相关
B.t的取值必定是3.15
C.回归直线一定过(4.5,3.5)
D.A产品每多生产1吨,则相应的生产能耗约增加0.7吨
【答案】B
【解析】由题意,eq \x\t(x)=eq \f(3+4+5+6,4)=4.5,因为=0.7x+0.35,所以 eq \x\t(y)=0.7×4.5+0.35=3.5,所以t=4×3.5-2.5-4-4.5=3,故选B.
6.(2019·泉州模拟)已知某产品连续4个月的广告费xi(千元)与销售额yi(万元),经过对这些数据的处理,得到如下数据信息:
①eq \i\su(i=1,4,x)i=18,eq \i\su(i=1,4,y)i=14;
②广告费用x和销售额y之间具有较强的线性相关关系;
③回归直线方程为中的=0.8(用最小二乘法求得).
那么广告费用为6千元时,可预测销售额约为( )
A.3.5万元 B.4.7万元
C.4.9万元 D.6.5万元
【答案】B
【解析】因为eq \i\su(i=1,4,x)i=18,eq \i\su(i=1,4,y)i=14,所以eq \x\t(x)=eq \f(9,2),eq \x\t(y)=eq \f(7,2),因为回归直线方程为中的=0.8,所以eq \f(7,2)=0.8×eq \f(9,2)+,所以=-eq \f(1,10),所以=0.8x-eq \f(1,10).故x=6时,可预测销售额约为4.7万元,故选B.
二、填空题
7.已知x,y的取值如下表.
从散点图分析,y与x线性相关,且回归方程为=1.46x+,则实数的值为________.
【答案】 -0.61
【解析】eq \x\t(x)=eq \f(2+3+4+5,4)=3.5,eq \x\t(y)=eq \f(2.2+3.8+5.5+6.5,4)=4.5,回归方程必过样本的中心点(eq \x\t(x),eq \x\t(y)).把(3.5,4.5)代入回归方程,计算得=-0.61.
8.高三某班学生每周用于物理学习的时间x(单位:小时)与物理成绩y(单位:分)之间有如下关系.
根据上表可得回归方程的斜率为3.53,则回归直线在y轴上的截距为________(精确到0.1).
【答案】13.5
【解析】由已知可得
eq \x\t(x)=eq \f(24+15+23+19+16+11+20+16+17+13,10)=17.4,
eq \x\t(y)=eq \f(92+79+97+89+64+47+83+68+71+59,10)=74.9,
设回归直线方程为=3.53x+,则74.9=3.53×17.4+,解得≈13.5.
9.(2019·长沙重点中学联考)在回归分析的问题中,我们可以通过对数变换把非线性回归方程y=c1ec2x(c1>0)转化为线性回归方程,即两边取对数,令z=ln y,得到z=c2x+ln c1.受其启发,可求得函数y=xlg2(4x)(x>0)的值域是________.
【答案】[eq \f(1,2),+∞)
【解析】 由题意,类比方法可得函数y=xlg2(4x)(x>0),两边取对数,可得lg2y=lg2(4x)lg2x,
令lg2x=t,则lg2y=t(2+t)=(t+1)2-1≥-1,
所以y≥eq \f(1,2),所以函数y=xlg2(4x)(x>0)的值域是[eq \f(1,2),+∞).
三、解答题
10.下表是高三某位文科生连续5次月考的历史、政治的成绩,结果统计如下.
(1)求该生5次月考历史成绩的平均分和政治成绩的方差;
(2)一般来说,学生的历史成绩与政治成绩有较强的线性相关关系,根据上表提供的数据,求两个变量x,y的线性回归方程.
附:eq \(b,\s\up18(^))=eq \f(\i\su(i=1,n, )(xi-\x\t(x))(yi-\x\t(y)),\i\su(i=1,n, )(xi-\x\t(x))2)=eq \f(\i\su(i=1,n,x)iyi-n\x\t(x) \x\t(y),\i\su(i=1,n,x)\\al(2,i)-n\x\t(x)2),eq \(a,\s\up18(^))=eq \x\t(y)-eq \(b,\s\up18(^))eq \x\t(x).
【答案】见解析
【解析】(1)eq \x\t(x)=eq \f(1,5)×(79+81+83+85+87)=83,
因为eq \x\t(y)=eq \f(1,5)×(77+79+79+82+83)=80,
所以seq \\al(2,y)=eq \f(1,5)×[(77-80)2+(79-80)2+(79-80)2+(82-80)2+(83-80)2]=4.8.
(2)因为eq \i\su(i=1,5, )(xi-eq \x\t(x))(yi-eq \x\t(y))=30,eq \i\su(i=1,5, )(xi-eq \x\t(x))2=40,
所以=0.75,=eq \x\t(y)-eq \x\t(x)=17.75,
则所求的线性回归方程为=0.75x+17.75.
11.(2019·石家庄调研)某学校高中毕业班有男生900人,女生600人,学校为了对高三学生数学学习情况进行分析,从高三年级按照性别进行分层抽样,抽取200名学生成绩,统计数据如下表所示.
(1)若成绩在90分以上(含90分),则成绩为合格,请估计该校毕业班平均成绩和及格学生人数;
(2)如果样本数据中,有60名女生数学成绩及格,请完成如下数学成绩与性别的列联表,并判断是否有90%的把握认为“该校学生的数学成绩与性别有关”.
参考公式:K2=eq \f(n(ad-bc)2,(a+b)(c+d)(a+c)(b+d))
【答案】见解析
【解析】(1)高三学生数学平均成绩为eq \f(1,200)×(60×20+80×40+100×70+120×50+140×20)=101,估计高三学生数学平均成绩为101分,及格学生人数为eq \f(70+50+20,200)×(900+600)=1 050.
(2)
K2的观测值k==eq \f(100,63)≈1.587
相关学案
这是一份专题11.1 坐标系-2022年高考数学一轮复习核心素养大揭秘学案,文件包含专题111坐标系解析版doc、专题111坐标系原卷版doc等2份学案配套教学资源,其中学案共24页, 欢迎下载使用。
这是一份专题11.2 参数方程-2022年高考数学一轮复习核心素养大揭秘学案,文件包含专题112参数方程解析版doc、专题112参数方程原卷版doc等2份学案配套教学资源,其中学案共28页, 欢迎下载使用。
这是一份专题10.2 随机抽样-2022年高考数学一轮复习核心素养大揭秘学案,文件包含专题102随机抽样解析版doc、专题102随机抽样原卷版doc等2份学案配套教学资源,其中学案共24页, 欢迎下载使用。









