（广东卷）2022年中考数学第一次模拟考试·

2022年中考数学第一次模拟考试【广东卷】

数  学（考试时间：90分钟  试卷满分：120分）

注意事项：

1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

5．考试范围：中考全部内容。

第Ⅰ卷

一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）

1．下列各数中，比小的数是（        ）

A． B．－ C． D．

2．京张高铁，京礼高速两条北京冬奥会重要交通保障设施投入使用后，将张家口、崇礼、延庆与北京城区串成一线．京张高铁开通运营一年累计发送旅客6 800 000人，大幅提升了京张两地通行能力，将6 800 000用科学记数法表示为（       ）

A． B． C． D．

3．看了《田忌赛马》故事后，数学兴趣小组用数学模型来分析：齐王与田忌的上中下三个等级的三匹马综合指标数如表，每匹马只赛一场，综合指标的两数相比，大数为胜，三场两胜则赢，已知齐王的三匹马出场顺序为6、4、2，若田忌的三匹马随机出场，则田忌能赢得比赛的概率为（       ）

A． B． C． D．

4．下列计算正确的是（       ）

A．x7÷x＝x7 B．(﹣3x2)2＝﹣9x4 C．x3•x3＝2x6 D．(x3)2＝x6

5．已知是方程的一个根．则的值为（       ）

A．4 B．6 C． D．

6．有5个大小一样的正方形制成如图所示的拼接图形（阴影部分），请你在图中的拼接图形上再拼接一个正方形，使新拼接成的图形折叠后能成为一个封闭的正方体盒子，在如图所示的A，B，C，D四个位置中，能够选择的位置有（　　）

A．1个 B．2个 C．3个 D．4个

7．如图，AB为⊙O的一条弦，C为⊙O上一点，OC∥AB．将劣弧AB沿弦AB翻折，交翻折后的弧AB交AC于点D．若D为翻折后弧AB的中点，则∠ABC＝（　　）

A．110° B．112.5° C．115° D．117.5°

8．阅读理解：如图1，在平面内选一定点O，引一条有方向的射线，再选定一个单位长度，那么平面上任一点M的位置可由的度数与的长度m确定，有序数对称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．

应用：在图2的极坐标系下，如果正六边形的边长为4，有一边在射线上，则正六边形的顶点C的极坐标应记为（       ）

A． B． C． D．

9．如图，在平面直角坐标系中，二次函数的图象与x轴交于A、C两点，与y轴交于点B，若P是x轴上一动点，点Q（0，2）在y轴上，连接PQ，则的最小值是（     ）

A．6 B． C． D．

10．如图，矩形ABCD的边CD上有一点E，，，垂足为F，将绕点F顺时针旋转，点E恰好落在点B处，点A落在EF上的点G处．下列结论：①；②；③；④若M为BG中点，则为等腰直角三角形；⑤B、G、O三点共线．正确的个数是（       ）

A．5 B．4 C．3 D．2

第Ⅱ卷

二、填空题（本大题共7小题，每小题4分，共28分）

11．设抛物线，其中为实数．将抛物线向上平移2个单位，所得抛物线顶点的纵坐标的最大值是__________

12．我国古代很早就对二元一次方程组进行了研究，古著《九章算术》记载用算筹表示二元一次方程组，发展到现代就是用矩阵式来表示二元一次方程组，而该方程组的解就是对应两直线（不平行）a1x+b1y＝c1与a2x+b2y＝c2的交点坐标P（x，y）据此，则矩阵式所对应两直线交点坐标是_________．

13．如图，在扇形OAB中，∠AOB＝105°，OA＝4，将扇形OAB沿着过点B的直线折叠，点O恰好落在弧的点D处，折痕BC交OA于点C，则阴影部分的面积为__________．

14．对于一个函数，自变量取时，函数值也等于，我们称为这个函数的不动点．如果二次函数有两个相异的不动点，，则______

15．已知二次函数的图象与x轴有两个交点，则下列说法在确的有：_____．（填序号）

①该二次函数的图象一定过定点；②若该函数图象开口向下，则m的取值范围为：；

③当且时，y的最小值为；④当，且该函数图象与x轴两交点的横坐标满足时，m的取值范围为：．

16．如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，E为AC边上的中点，连接BE交AD于F，将△AFE沿若AC翻折到△AGE，若四边形AFEG恰好为菱形，连接BG，则tan∠ABG=________．

17．如图，在中，，，，点P在边AC上运动（可与点A，C重合），将线段BP绕点P逆时针旋转120°，得到线段DP，连接BD，CD，则CD长的最小值为______．

 三、解答题（本大题共8小题，共62分．解答应写出文字说明、证明过程或演算步骤）

18．（本题满分6分）（1）计算：；（2）解不等式组：

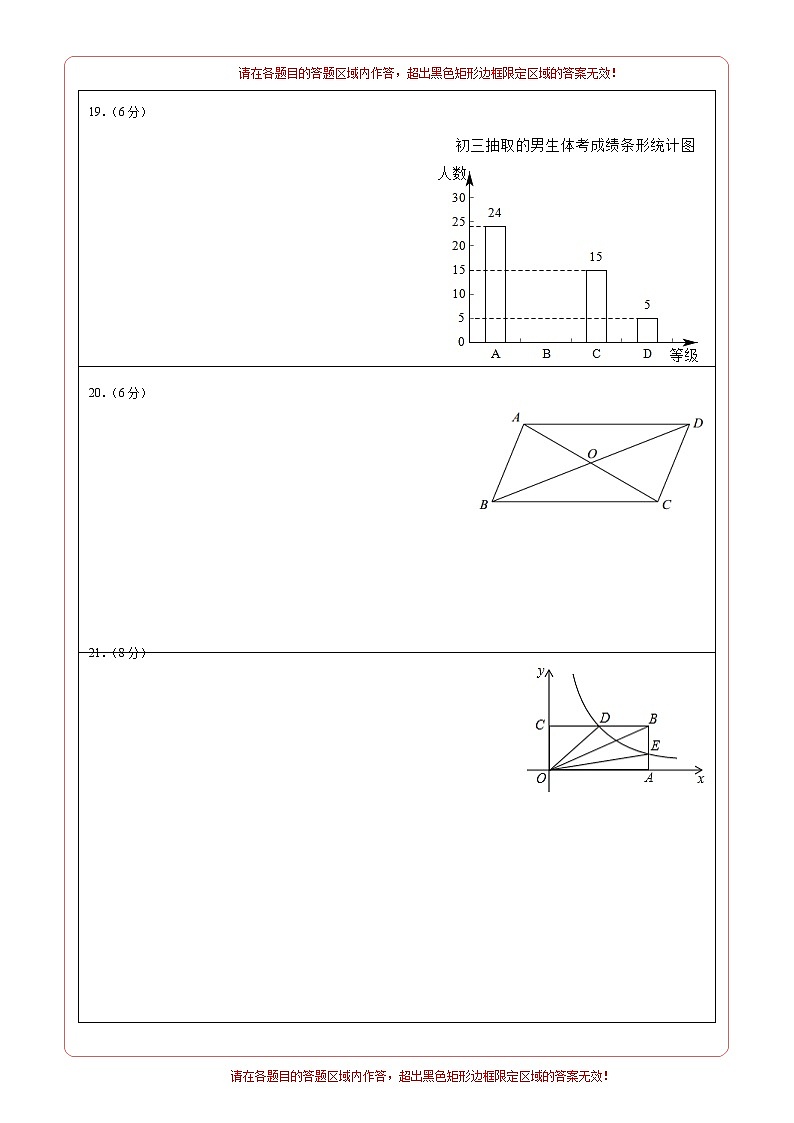
19．（本题满分6分）距离2022年中招体育考试的时间已经越来越近，某校初三年级为了了解本校学生在平时体育训练的效果，随机抽取了男、女各60名考生的体考成绩，并将数据进行整理分析，给出了下面部分信息：数据分为A，B，C，D四个等级分别是：

A：，B：，C：，D：

60名男生成绩的条形统计图以及60名女生成绩的扇形统计图如图：

男生成绩在B组的前10名考生的分数为：

47.5，47.5，47.5，47，47，47，46，45.5，45，45．

60名男生和60名女生成绩的平均数，中位数，众数如下：

根据以上信息，解答下列问题：(1)填空：______，______，并补全条形统计图．

(2)根据以上数据，你认为在此次考试中，男生成绩好还是女生成绩好？请说明理由（说明一条理由即可）．

(3)若该年级有800名学生，请估计该年级所有参加体考的考生中，成绩为A等级的考生人数．

20．（本题满分6分）如图，四边形为平行四边形，连接、交于点．

(1)请用尺规完成基本作图：过点作直线的垂线，垂足为；在直线上作点使得，连接（保留作图痕迹，不写作法）

(2)在（1）的条件下，若，求证：．

21．（本题满分8分）如图，在平面直角坐标系中，点为坐标系原点，矩形的边，分别在轴和轴上，其中，．已知反比例函数的图象经过边上的中点，交于点． (1)求的值；(2)猜想的面积与的面积之间的关系，请说明理由．(3)若点在该反比例函数的图象上运动（不与点重合），过点作轴于点，作所在直线于点，记四边形的面积为，求关于的解析式并写出的取值范围．

22．（本题满分8分）某运动品牌专卖店准备购进甲、乙两种运动鞋．其中甲、乙两种运动鞋的进价和售价如表（用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同）．

（1）求m的值；（2）要使购进的甲、乙两种运动鞋共200双的总利润（利润＝售价﹣进价）不少于21700元，且甲种运动鞋的数量不超过100双，问该专卖店共有几种进货方案？

（3）在（2）的条件下，专卖店准备对甲种运动鞋进行每双优惠a（50＜a＜70）元的优惠促销活动，乙种运动鞋价格不变．那么该专卖店要获得最大利润应如何进货？

23．（本题满分8分）如图1，CD是的弦，半径，垂足为B，过点C作的切线l．

(1)若点E在上，且，连接OE．①连接AE，求证：；②如图2，若B是OA的中点，连接OD，求证：DE是的直径；(2)如图3，过点B作，垂足为F，若的半径是4，求的最大值．

24．（本题满分10分）如图，在正方形ABCD中，点E在直线AD右侧，且AE＝1，以DE为边作正方形DEFG，射线DF与边BC交于点M，连接ME，MG．

 (1)如图1，求证：ME＝MG；(2)若正方形ABCD的边长为4，①如图2，当G，C，M三点共线时，设EF与BC交于点N，求的值；②如图3，取AD中点P，连接PF，求PF长度的最大值．

25．（本题满分10分）抛物线y＝x2﹣1交x轴于A，B两点（A在B的左边）．

(1)▱ACDE的顶点C在y轴的正半轴上，顶点E在y轴右侧的抛物线上；

①如图（1），若点C的坐标是（0，3），点E的横坐标是，直接写出点A，D的坐标．

②如图（2），若点D在抛物线上，且▱ACDE的面积是12，求点E的坐标．

(2)如图（3），F是原点O关于抛物线顶点的对称点，不平行y轴的直线l分别交线段AF，BF（不含端点）于G，H两点．若直线l与抛物线只有一个公共点，求证：FG＋FH的值是定值．