专题5.1 平面向量的概念及线性运算-2022年高考数学（理）一轮复习-题型全归纳与高效训练突破学案

这是一份专题5.1 平面向量的概念及线性运算-2022年高考数学（理）一轮复习-题型全归纳与高效训练突破学案，文件包含专题51平面向量的概念及线性运算解析版docx、专题51平面向量的概念及线性运算原卷版docx等2份学案配套教学资源，其中学案共33页， 欢迎下载使用。
目录
TOC \ "1-3" \h \u 一、题型全归纳1
题型一 平面向量的基本概念1
题型二 平面向量的线性运算3
题型三 平面向量共线定理的应用6
命题角度1 证明向量共线或三点共线6
命题角度2 由向量共线求参数的值7
命题角度3 证明三点共线7
题型四 共线定理的推广与应用8
二、高效训练突破10
一、题型全归纳
题型一 平面向量的基本概念
【题型要点】1．向量的有关概念
(1)向量：既有大小又有方向的量叫做向量，向量的大小叫做向量的模．
(2)零向量：长度为0的向量，其方向是任意的．
(3)单位向量：长度等于1个单位的向量．
(4)平行向量：方向相同或相反的非零向量，又叫共线向量，规定：0与任一向量共线．
(5)相等向量：长度相等且方向相同的向量．
(6)相反向量：长度相等且方向相反的向量．
2.五个特殊向量
(1)要注意0与0的区别，0是一个实数，0是一个向量，且|0|＝0.
(2)单位向量有无数个，它们大小相等，但方向不一定相同．
(3)任一组平行向量都可以平移到同一直线上，因此平行向量也叫做共线向量．
(4)与向量a平行的单位向量有两个，即向量eq \f(a,|a|)和－eq \f(a,|a|).
3.辨析向量有关概念的五个关键点
(1)向量定义的关键是方向和长度．
(2)非零共线向量的关键是方向相同或相反，长度没有限制．
(3)相等向量的关键是方向相同且长度相等．
(4)单位向量的关键是方向没有限制，但长度都是一个单位长度．
(5)零向量的关键是方向没有限制，长度是0，规定零向量与任何向量共线．
【例1】下列叙述错误的是________(填序号)．
①已知向量a∥b，且|a|>|b|>0，则向量a＋b的方向与向量a的方向相同；
②|a|＋|b|＝|a＋b|⇔a与b方向相同；
③向量b与向量a共线的充要条件是有且只有一个实数λ，使得b＝λa；
④eq \(AB,\s\up6(→))＋eq \(BA,\s\up6(→))＝0；
⑤若λa＝λb，则a＝b.
【答案】②③④⑤
【解析】对于①，当a和b方向相同，则它们的和的方向应该与a(或b)的方向相同；当a和b方向相反，而a的模大于b的模，则它们的和的方向与a的方向相同．
对于②，当a，b之一为零向量时结论不成立．
对于③，当a＝0且b＝0时，λ有无数个值；当a＝0但b≠0时，λ不存在．
对于④，由于两个向量之和仍是一个向量，所以eq \(AB,\s\up6(→))＋eq \(BA,\s\up6(→))＝0.
对于⑤，当λ＝0时，无论a与b的大小与方向如何，都有λa＝λb，此时不一定有a＝b.
故②③④⑤均错误．
【例2】下列命题中，正确的个数是( )
①若两个向量相等，则它们的起点和终点分别重合；
②若|a|＝|b|，则a＝b或a＝－b；
③若λa＝0(λ为实数)，则λ必为零；
④已知λ，μ为实数，若λa＝μb，则a与b共线．
A．0 B．1
C．2 D．3
【答案】A
【解析】①错误，如在▱ABCD中，eq \(AD,\s\up6(→))＝eq \(BC,\s\up6(→))，但是这两个向量的起点和终点分别不重合；②错误，模相等的两个向量，方向关系不确定；③错误，若λa＝0(λ为实数)，则λ＝0或a＝0；④错误，当λ＝μ＝0时，λa＝μb＝0，但a与b不一定共线．
题型二 平面向量的线性运算
【题型要点】
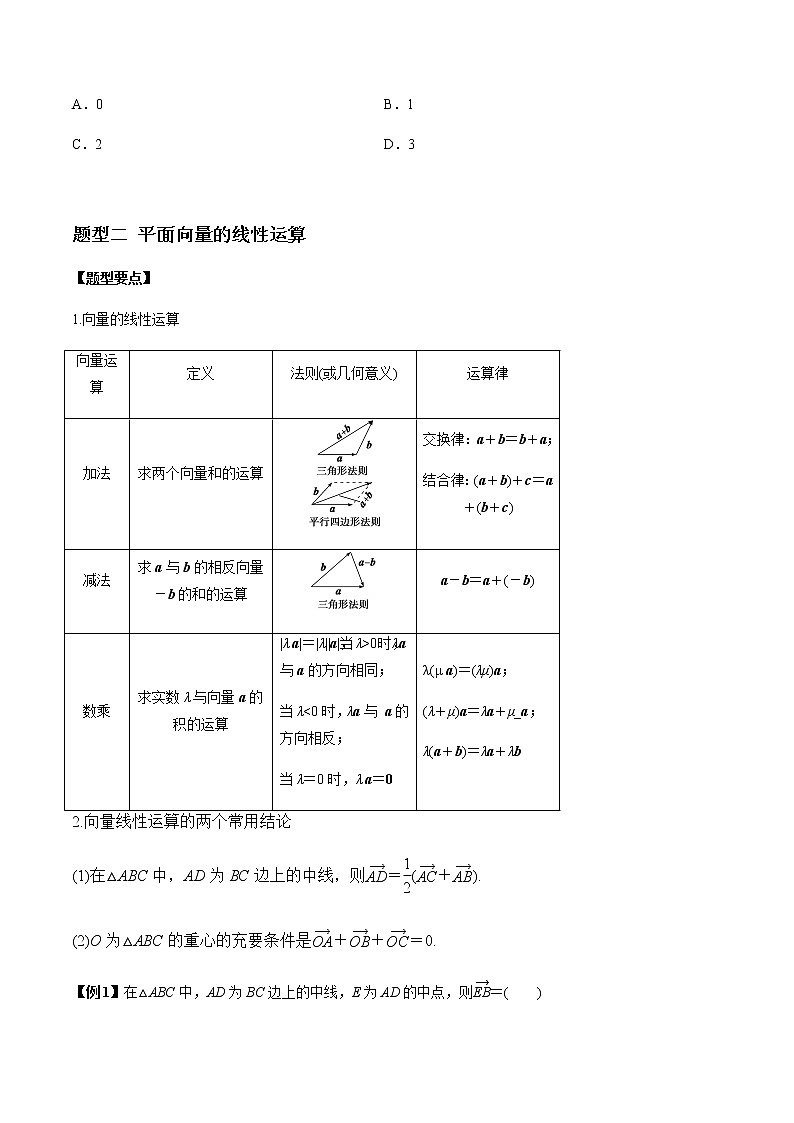
1.向量的线性运算
2.向量线性运算的两个常用结论
(1)在△ABC中，AD为BC边上的中线，则eq \(AD,\s\up6(→))＝eq \f(1,2)(eq \(AC,\s\up6(→))＋eq \(AB,\s\up6(→))).
(2)O为△ABC的重心的充要条件是eq \(OA,\s\up6(→))＋eq \(OB,\s\up6(→))＋eq \(OC,\s\up6(→))＝0.
【例1】在△ABC中，AD为BC边上的中线，E为AD的中点，则eq \(EB,\s\up6(→))＝( )
A.eq \f(3,4)eq \(AB,\s\up6(→))－eq \f(1,4)eq \(AC,\s\up6(→)) B．eq \f(1,4)eq \(AB,\s\up6(→))－eq \f(3,4)eq \(AC,\s\up6(→))
C.eq \f(3,4)eq \(AB,\s\up6(→))＋eq \f(1,4)eq \(AC,\s\up6(→)) D．eq \f(1,4)eq \(AB,\s\up6(→))＋eq \f(3,4)eq \(AC,\s\up6(→))
【答案】A
【解析】
法一：如图所示，eq \(EB,\s\up6(→))＝eq \(ED,\s\up6(→))＋eq \(DB,\s\up6(→))＝eq \f(1,2)eq \(AD,\s\up6(→))＋eq \f(1,2)eq \(CB,\s\up6(→))＝eq \f(1,2)×eq \f(1,2)(eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→)))＋eq \f(1,2)(eq \(AB,\s\up6(→))－eq \(AC,\s\up6(→)))＝eq \f(3,4)eq \(AB,\s\up6(→))－eq \f(1,4)eq \(AC,\s\up6(→))，故选A.
法二：eq \(EB,\s\up6(→))＝eq \(AB,\s\up6(→))－eq \(AE,\s\up6(→))＝eq \(AB,\s\up6(→))－eq \f(1,2)eq \(AD,\s\up6(→))＝eq \(AB,\s\up6(→))－eq \f(1,2)×eq \f(1,2)(eq \(AB,\s\up6(→))＋eq \(AC,\s\up6(→)))＝eq \f(3,4)eq \(AB,\s\up6(→))－eq \f(1,4)eq \(AC,\s\up6(→))，故选A.
【例2】(2020云南省楚雄州十校联考)如图，在直角梯形ABCD中，eq \(DC,\s\up6(→))＝eq \f(1,4)eq \(AB,\s\up6(→))，eq \(BE,\s\up6(→))＝2eq \(EC,\s\up6(→))，且eq \(AE,\s\up6(→))＝req \(AB,\s\up6(→))＋seq \(AD,\s\up6(→))，则2r＋3s＝( )
A．1 B．2
C．3 D．4
【答案】C
【解析】 法一：由题图可得eq \(AE,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \(BE,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \f(2,3)eq \(BC,\s\up6(→))＝eq \(AB,\s\up6(→))＋eq \f(2,3)(eq \(BA,\s\up6(→))＋eq \(AD,\s\up6(→))＋eq \(DC,\s\up6(→)))＝eq \f(1,3)eq \(AB,\s\up6(→))＋eq \f(2,3)(eq \(AD,\s\up6(→))＋eq \(DC,\s\up6(→)))＝eq \f(1,3)eq \(AB,\s\up6(→))＋eq \f(2,3)(eq \(AD,\s\up6(→))＋eq \f(1,4)eq \(AB,\s\up6(→)))＝eq \f(1,2)eq \(AB,\s\up6(→))＋eq \f(2,3)eq \(AD,\s\up6(→)).因为eq \(AE,\s\up6(→))＝req \(AB,\s\up6(→))＋seq \(AD,\s\up6(→))，所以r＝eq \f(1,2)，s＝eq \f(2,3)，则2r＋3s＝1＋2＝3.
法二：因为eq \(BE,\s\up6(→))＝2eq \(EC,\s\up6(→))，所以eq \(AE,\s\up6(→))－eq \(AB,\s\up6(→))＝2(eq \(AC,\s\up6(→))－eq \(AE,\s\up6(→)))，整理，得eq \(AE,\s\up6(→))＝eq \f(1,3)eq \(AB,\s\up6(→))＋eq \f(2,3)eq \(AC,\s\up6(→))＝eq \f(1,3)eq \(AB,\s\up6(→))＋eq \f(2,3)(eq \(AD,\s\up6(→))＋eq \(DC,\s\up6(→)))＝eq \f(1,2)eq \(AB,\s\up6(→))＋eq \f(2,3)eq \(AD,\s\up6(→))，以下同法一．
法三：如图，延长AD，BC交于点P，则由eq \(DC,\s\up6(→))＝eq \f(1,4)eq \(AB,\s\up6(→))得DC∥AB，且AB＝4DC.
又eq \(BE,\s\up6(→))＝2eq \(EC,\s\up6(→))，所以E为PB的中点，且eq \(AP,\s\up6(→))＝eq \f(4,3)eq \(AD,\s\up6(→)).
于是，eq \(AE,\s\up6(→))＝eq \f(1,2)(eq \(AB,\s\up6(→))＋eq \(AP,\s\up6(→)))＝eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\(AB,\s\up6(→))＋\f(4,3)\(AD,\s\up6(→))))＝eq \f(1,2)eq \(AB,\s\up6(→))＋eq \f(2,3)eq \(AD,\s\up6(→)).以下同法一．
法四：如图，建立平面直角坐标系xAy，依题意可设点B(4m，0)，D(3m，3h)，E(4m，2h)，其中m＞0，h＞0.
由eq \(AE,\s\up6(→))＝req \(AB,\s\up6(→))＋seq \(AD,\s\up6(→))，得(4m，2h)＝r(4m，0)＋s(3m，3h)，
所以eq \b\lc\{(\a\vs4\al\c1(4m＝4mr＋3ms，,2h＝3hs，))解得eq \b\lc\{(\a\vs4\al\c1(r＝\f(1,2)，,s＝\f(2,3)，))
所以2r＋3s＝1＋2＝3.
题型三 平面向量共线定理的应用
【题型要点】求解向量共线问题的注意事项
(1)向量共线的充要条件中，当两向量共线时，通常只有非零向量才能表示与之共线的其他向量，注意待定系数法和方程思想的运用.
(2)证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得到三点共线．
(3)若a与b不共线且λa＝μb，则λ＝μ＝0.
(4)直线的向量式参数方程，A，P，B三点共线⇔eq \(OP,\s\up6(→))＝(1－t)eq \(OA,\s\up6(→))＋teq \(OB,\s\up6(→))(O为平面内任一点，t∈R)．
eq \(OA,\s\up6(→))＝λeq \(OB,\s\up6(→))＋μeq \(OC,\s\up6(→))(λ，μ为实数)，若A，B，C三点共线，则λ＋μ＝1.
命题角度1 证明向量共线或三点共线
【例1】已知平面内一点P及△ABC，若eq \(PA,\s\up6(→))＋eq \(PB,\s\up6(→))＋eq \(PC,\s\up6(→))＝eq \(AB,\s\up6(→))，则点P与△ABC的位置关系是( )
A．点P在线段AB上 B．点P在线段BC上
C．点P在线段AC上 D．点P在△ABC外部
【答案】C
【解析】因为eq \(PA,\s\up6(→))＋eq \(PB,\s\up6(→))＋eq \(PC,\s\up6(→))＝eq \(AB,\s\up6(→))＝eq \(PB,\s\up6(→))－eq \(PA,\s\up6(→))，所以eq \(PC,\s\up6(→))＝－2eq \(PA,\s\up6(→))，所以A，P，C三点共线，且P是线段AC的三等分点(靠近A)．
【升华】证明向量共线：对于向量a，b，若存在实数λ，使a＝λb(b≠0)，则a与b共线．
命题角度2 由向量共线求参数的值
【例2】(2020·安徽合肥一中高考模拟)如图，在平行四边形ABCD中，M，N分别为AB，AD上的点，且eq \(AM,\s\up6(→))＝eq \f(4,5)eq \(AB,\s\up6(→))，连接AC，MN交于点P，若eq \(AP,\s\up6(→))＝eq \f(4,11)eq \(AC,\s\up6(→))，则点N在AD上的位置为( )
A．AD中点
B．AD上靠近点D的三等分点
C．AD上靠近点D的四等分点
D．AD上靠近点D的五等分点
【答案】B
【解析】设eq \(AD,\s\up6(→))＝λeq \(AN,\s\up6(→))，因为eq \(AP,\s\up6(→))＝eq \f(4,11)eq \(AC,\s\up6(→))＝eq \f(4,11)(eq \(AB,\s\up6(→))＋eq \(AD,\s\up6(→)))＝eq \f(4,11)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,4)\(AM,\s\up6(→))＋λ\(AN,\s\up6(→))))＝eq \f(5,11)eq \(AM,\s\up6(→))＋eq \f(4λ,11)eq \(AN,\s\up6(→))，又M，N，P三点共线，所以eq \f(5,11)＋eq \f(4λ,11)＝1，解得λ＝eq \f(3,2)，所以eq \(AN,\s\up6(→))＝eq \f(2,3)eq \(AD,\s\up6(→))，所以点N在AD上靠近点D的三等分点．
【升华】求参数的值：利用共线向量定理及向量相等的条件列方程(组)求参数的值．
命题角度3 证明三点共线
【例3】(2020·江西吉安一中、新余一中等八所中学联考)设两个非零向量a与b不共线．
(1)若eq \(AB,\s\up6(→))＝a＋b，eq \(BC,\s\up6(→))＝2a＋8b，eq \(CD,\s\up6(→))＝3(a－b)，求证：A，B，D三点共线；
(2)试确定实数k，使ka＋b和a＋kb共线．
【答案】见解析
【解析】 (1)证明：因为eq \(AB,\s\up6(→))＝a＋b，eq \(BC,\s\up6(→))＝2a＋8b，eq \(CD,\s\up6(→))＝3(a－b)，所以eq \(BD,\s\up6(→))＝eq \(BC,\s\up6(→))＋eq \(CD,\s\up6(→))＝2a＋8b＋3(a－b)＝5(a＋b)＝5eq \(AB,\s\up6(→))，
所以eq \(AB,\s\up6(→))，eq \(BD,\s\up6(→))共线，又它们有公共点B，
所以A，B，D三点共线．
(2)因为ka＋b与a＋kb共线，
所以存在实数λ，使ka＋b＝λ(a＋kb)，
即(k－λ)a＝(λk－1)b.
又a，b是两个不共线的非零向量，
所以k－λ＝λk－1＝0.所以k2－1＝0.
所以k＝±1.
【规律】证明三点共线：若存在实数λ，使eq \(AB,\s\up6(→))＝λeq \(AC,\s\up6(→))，则A，B，C三点共线．
题型四 共线定理的推广与应用
【题型要点】
一、共线定理：已知eq \(PA,\s\up6(→))，eq \(PB,\s\up6(→))为平面内两个不共线的向量，设eq \(PC,\s\up6(→))＝xeq \(PA,\s\up6(→))＋yeq \(PB,\s\up6(→))，则A，B，C三点共线的充要条件为x＋y＝1.
二、推广形式：如图所示，直线DE∥AB，C为直线DE上任一点，设eq \(PC,\s\up6(→))＝xeq \(PA,\s\up6(→))＋yeq \(PB,\s\up6(→))(x，y∈R)．
当直线DE不过点P时，直线PC与直线AB的交点记为F，因为点F在直线AB上，所以由三点共线结论可知，若eq \(PF,\s\up6(→))＝λeq \(PA,\s\up6(→))＋μeq \(PB,\s\up6(→))(λ，μ∈R)，则λ＋μ＝1.由△PAB与△PED相似，知必存在一个常数m∈R，使得eq \(PC,\s\up6(→))＝m eq \(PF,\s\up6(→))，则eq \(PC,\s\up6(→))＝meq \(PF,\s\up6(→))＝mλeq \(PA,\s\up6(→))＋mμeq \(PB,\s\up6(→)).
又eq \(PC,\s\up6(→))＝xeq \(PA,\s\up6(→))＋yeq \(PB,\s\up6(→))(x，y∈R)，
所以x＋y＝mλ＋mμ＝m.
以上过程可逆．
因此得到结论：eq \(PC,\s\up6(→))＝xeq \(PA,\s\up6(→))＋yeq \(PB,\s\up6(→))，
则x＋y＝m(定值)，反之亦成立．
【例1】(2020·江西上饶重点中学六校联考)如图所示，A，B，C是圆O上的三点，线段CO的延长线与BA的延长线交于圆O外一点D，若eq \(OC,\s\up6(→))＝meq \(OA,\s\up6(→))＋neq \(OB,\s\up6(→))，则m＋n的取值范围是________．
【答案】 (－1，0)
【解析】 由点D是圆O外的一点，可设eq \(BD,\s\up6(→))＝λeq \(BA,\s\up6(→))(λ＞1)，则eq \(OD,\s\up6(→))＝eq \(OB,\s\up6(→))＋eq \(BD,\s\up6(→))＝eq \(OB,\s\up6(→))＋λeq \(BA,\s\up6(→))＝λeq \(OA,\s\up6(→))＋(1－λ)eq \(OB,\s\up6(→)).因为C，O，D三点共线，令eq \(OD,\s\up6(→))＝－μeq \(OC,\s\up6(→))(μ＞1)，所以eq \(OC,\s\up6(→))＝－eq \f(λ,μ)eq \(OA,\s\up6(→))－eq \f(1－λ,μ)·eq \(OB,\s\up6(→))(λ＞1，μ＞1)．因为eq \(OC,\s\up6(→))＝meq \(OA,\s\up6(→))＋neq \(OB,\s\up6(→))，所以m＝－eq \f(λ,μ)，n＝－eq \f(1－λ,μ)，则m＋n＝－eq \f(λ,μ)－eq \f(1－λ,μ)＝－eq \f(1,μ)∈(－1，0)．
【例2】 如图，在扇形OAB中，∠AOB＝eq \f(π,3)，C为弧AB上的动点，若eq \(OC,\s\up6(→))＝xeq \(OA,\s\up6(→))＋yeq \(OB,\s\up6(→))，则x＋3y的取值范围是________．
【答案】 [1，3]
【解析】 eq \(OC,\s\up6(→))＝xeq \(OA,\s\up6(→))＋3yeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\(OB,\s\up6(→)),3)))，如图，作eq \(OB′,\s\up6(→))＝eq \f(\(OB,\s\up6(→)),3)，则考虑以向量eq \(OA,\s\up6(→))，eq \(OB′,\s\up6(→))为基底．显然，当C在A点时，经过m＝1的平行线，当C在B点时，经过m＝3的平行线，这两条
线分别是最近与最远的平行线，所以x＋3y的取值范围是[1，3]．
二、高效训练突破
一、选择题
1．设a0为单位向量，①若a为平面内的某个向量，则a＝|a|a0；②若a与a0平行，则a＝|a|a0；③若a与a0平行且|a|＝1，则a＝a0.上述命题中，假命题的个数是( )
A．0 B．1
C．2 D．3
【答案】D.
【解析】：向量是既有大小又有方向的量，a与|a|a0的模相同，但方向不一定相同，故①是假命题；若a与a0平行，则a与a0的方向有两种情况：一是同向，二是反向，反向时a＝－|a|a0，故②③也是假命题．综上所述，假命题的个数是3.
2．设a，b都是非零向量，下列四个条件中，使eq \f(a,|a|)＝eq \f(b,|b|)成立的充分条件是( )
A．a＝－b B．a∥b
C．a＝2b D．a∥b且|a|＝|b|
【答案】C.
【解析】：因为向量eq \f(a,|a|)的方向与向量a相同，向量eq \f(b,|b|)的方向与向量b相同，且eq \f(a,|a|)＝eq \f(b,|b|)，所以向量a与向量b方向相同，故可排除选项A，B，D.当a＝2b时，eq \f(a,|a|)＝eq \f(2b,|2b|)＝eq \f(b,|b|)，故“a＝2b”是“eq \f(a,|a|)＝eq \f(b,|b|)”成立的充分条件．
3.已知向量a，b不共线，且c＝λa＋b，d＝a＋(2λ－1)b，若c与d反向共线，则实数λ的值为( )
A．1 B．－eq \f(1,2)
C．1或－eq \f(1,2) D．－1或－eq \f(1,2)
【答案】B
【解析】由于c与d反向共线，则存在实数k使c＝kd(k