



专题8.2 空间点、直线、平面之间的位置关系-2022年高考数学(理)一轮复习-题型全归纳与高效训练突破学案
展开目录
TOC \ "1-3" \h \u \l "_Tc27691" 一、考点全归纳 PAGEREF _Tc27691 1
\l "_Tc32274" 二 题型全归纳 PAGEREF _Tc32274 3
\l "_Tc8773" 题型一 平面的基本性质及其应用 PAGEREF _Tc8773 3
\l "_Tc15721" 题型二 空间两直线位置关系的判定 PAGEREF _Tc15721 5
\l "_Tc21623" 题型三 异面直线所成的角 PAGEREF _Tc21623 6
\l "_Tc5835" 题型四 构造平面研究直线相交问题 PAGEREF _Tc5835 9
\l "_Tc13958" 三、高效训练突破 PAGEREF _Tc13958 11
一、考点全归纳
1.四个公理
公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
公理2:过不在一条直线上的三点,有且只有一个平面.
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
公理4:平行于同一条直线的两条直线互相平行.
2.空间直线的位置关系
(1)位置关系的分类
eq \b\lc\{(\a\vs4\al\c1(共面直线\b\lc\{(\a\vs4\al\c1(平行,相交)),异面直线:不同在任何一个平面内))
(2)异面直线所成的角
①定义:设a,b是两条异面直线,经过空间中任一点O作直线a′∥a,b′∥b,把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角);
②范围:eq \b\lc\(\rc\](\a\vs4\al\c1(0,\f(π,2))).
(3)定理
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.
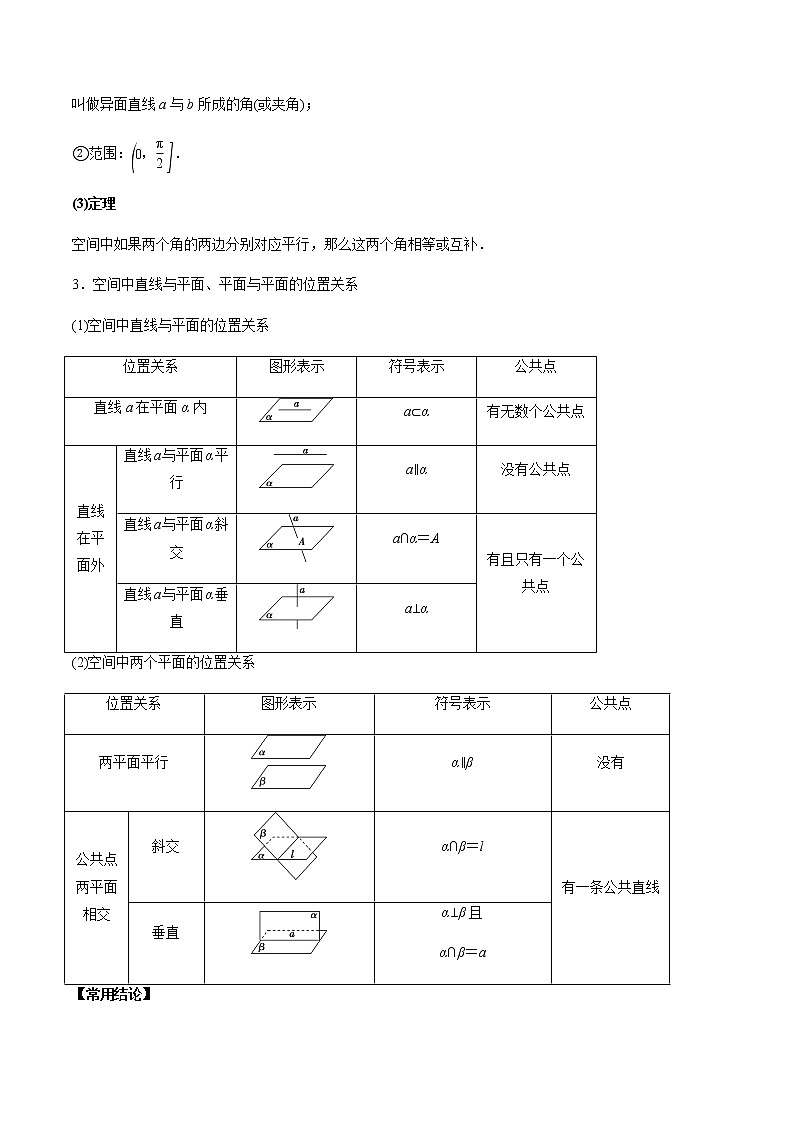
3.空间中直线与平面、平面与平面的位置关系
(1)空间中直线与平面的位置关系
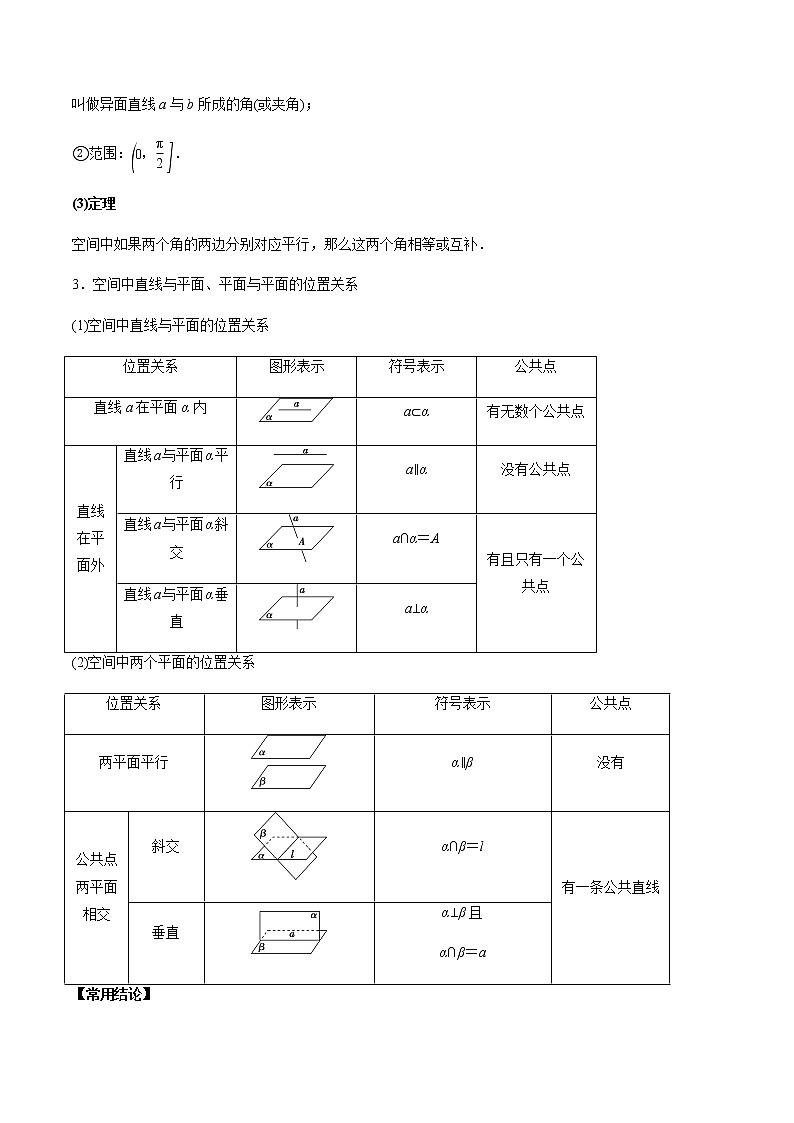
(2)空间中两个平面的位置关系
【常用结论】
1.唯一性定理
(1)过直线外一点有且只有一条直线与已知直线平行.
(2)过直线外一点有且只有一个平面与已知直线垂直.
(3)过平面外一点有且只有一个平面与已知平面平行.
(4)过平面外一点有且只有一条直线与已知平面垂直.
2.异面直线的判定定理
经过平面内一点的直线与平面内不经过该点的直线互为异面直线.
二 题型全归纳
题型一 平面的基本性质及其应用
【题型要点】1.三个公理是立体几何的基础.公理1是确定直线在平面内的依据;公理2是利用点或直线确定平面的依据;公理3是确定两个平面有一条交线的依据,同时也是证明多点共线、多线共点的依据.
2.证明点共线或线共点的问题,关键是转化为证明点在直线上,也就是利用公理3,证明点在两个平面的交线上,或者选择其中两点确定一条直线,然后证明另一点也在该直线上.
3.共面、共线、共点问题的证明
(1)证明共面的方法:①先确定一个平面,然后再证其余的线(或点)在这个平面内;②证两平面重合.
(2)证明共线的方法:①先由两点确定一条直线,再证其他各点都在这条直线上;②直接证明这些点都在同一条特定直线上.
(3)证明线共点问题的常用方法是:先证其中两条直线交于一点,再证其他直线经过该点.
【例1】在正方体ABCDA1B1C1D1中,判断下列说法是否正确,并说明理由.
(1)直线AC1在平面CC1B1B内;
(2)设正方形ABCD与正方形A1B1C1D1的中心分别为O,O1,则平面AA1C1C与平面BB1D1D的交线为OO1;
(3)由点A,O,C可以确定一个平面;
(4)由A,C1,B1确定的平面是ADC1B1;
(5)设直线l是平面ABCD内的直线,直线m是平面DD1C1C内的直线,若l与m相交,则交点一定在直线CD上.
【例2】1.(2020·衡水中学模拟)有下列四个命题:
①空间四点共面,则其中必有三点共线;
②空间四点不共面,则其中任意三点不共线;
③空间四点中有三点共线,则此四点共面;
④空间四点中任意三点不共线,则此四点不共面.
其中真命题的所有序号有________.
题型二 空间两直线位置关系的判定
【题型要点】(1)异面直线的判定方法
(2)构造法判断空间两直线的位置关系
对于线面、面面平行、垂直的位置关系的判定,可构造长方体或正方体化抽象为直观去判断,可避免因考虑不全面而导致错误,构造法实质上是结合题意构造符合题意的直观模型,然后将问题利用模型直观地作出判断,这样减少了抽象性.
【例1】(2019·高考全国卷Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则( )
A.BM=EN,且直线BM,EN是相交直线
B.BM≠EN,且直线BM,EN是相交直线
C.BM=EN,且直线BM,EN是异面直线
D.BM≠EN,且直线BM,EN是异面直线
【例2】下图中,G,N,M,H分别是正三棱柱(两底面为正三角形的直棱柱)的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有( )
A.①③ B.②③
C.②④ D.②③④
题型三 异面直线所成的角
【题型要点】异面直线所成的角
1.平移法求异面直线所成角的一般步骤
(1)作角——用平移法找(或作)出符合题意的角.
(2)求角——转化为求一个三角形的内角,通过解三角形,求出角的大小.
【提醒】:异面直线所成的角θ∈(0,eq \f(π,2)].
2.坐标法求异面直线所成的角:当题设中含有两两垂直的三边关系时,常采用坐标法.
【提醒】:如果求出的角是锐角或直角,则它就是要求的角;如果求出的角是钝角,则它的补角才是要求的角.
【例1】在长方体ABCDA1B1C1D1中,AB=BC=1,AA1=eq \r(3),则异面直线AD1与DB1所成角的余弦值为( )
A.eq \f(1,5) B.eq \f(\r(5),6)
C.eq \f(\r(5),5) D.eq \f(\r(2),2)
【例2】如图所示,A是△BCD所在平面外的一点,E,F分别是BC,AD的中点.
①求证:直线EF与BD是异面直线;
②若AC⊥BD,AC=BD,求EF与BD所成的角.
题型四 构造平面研究直线相交问题
【题型要点】(1)平面几何和立体几何在点、线、面的位置关系中有很多的不同,借助确定的几何模型,利用直观想象讨论点、线、面的位置关系在平面和空间中的差异.
(2)本题难度不大,但比较灵活.对平面的基本性质、空间两条直线的位置关系的考查难度一般都不会太大.
(3)注意本题解法较多,但关键在于构造平面,但不少学生不会构造平面,因此失分较多.
【例1】设l是直线,α,β是两个不同的平面,则下列说法正确的是( )
A.若l∥α,l∥β,则α∥β
B.若l∥α,l⊥β,则α⊥β
C.若α⊥β,l⊥α,则l⊥β
D.若α⊥β,l∥α,则l⊥β
【例2】在正方体ABCDA1B1C1D1中,E,F分别为棱AA1、CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线有________条.
三、高效训练突破
一、选择题
1.在空间四边形ABCD各边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF,GH相交于点P,那么( )
A.点P必在直线AC上
B.点P必在直线BD上
C.点P必在平面DBC内
D.点P必在平面ABC外
2.如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,则这四个点不共面的一个图是( )
3.四条线段顺次首尾相连,它们最多可确定的平面个数有( )
A.4个 B.3个
C.2个 D.1个
4.已知l1,l2,l3是空间三条不同的直线,则下列命题正确的是( )
A.l1⊥l2,l2⊥l3⇒l1∥l3
B.l1⊥l2,l2∥l3⇒l1⊥l3
C.l1∥l2∥l3⇒l1,l2,l3共面
D.l1,l2,l3共点⇒l1,l2,l3共面
5.如图,ABCDA1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确的是( )
A.A,M,O三点共线 B.A,M,O,A1不共面
C.A,M,C,O不共面 D.B,B1,O,M共面
6.(2020·广东东莞模拟)如图,在三棱柱ABCA1B1C1中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC的中点,则下列叙述正确的是( )
A.CC1与B1E是异面直线
B.AC⊥平面ABB1A1
C.AE,B1C1为异面直线,且AE⊥B1C1
D.A1C1∥平面AB1E
7.(2020·太原模拟)在正三棱柱ABCA1B1C1中,若AB=BB1,D是CC1的中点,则CA1与BD所成角的大小是( )
A.eq \f(π,3) B.eq \f(5π,12)
C.eq \f(π,2) D.eq \f(7π,12)
8.在各棱长均相等的直三棱柱ABCA1B1C1中,已知M是棱BB1的中点,N是棱AC的中点,则异面直线A1M与BN所成角的正切值为( )
A.eq \r(3) B.1
C.eq \f(\r(6),3) D.eq \f(\r(2),2)
9.(2020·广东深圳二模)已知正方体ABCDA1B1C1D1,P为棱CC1上的动点,Q为棱AA1的中点,设直线m为平面BDP与平面B1D1P的交线,则( )
A.m∥D1Q B.m∥平面B1D1Q
C.m⊥B1Q D.m⊥平面ABB1A1
10.在棱长为1的正方体ABCDA1B1C1D1中,E,F分别是DD1和AB的中点,平面B1EF交棱AD于点P,则PE=( )
A.eq \f(\r(15),6) B.eq \f(2\r(3),3) C.eq \f(\r(3),2) D.eq \f(\r(13),6)
11.如图,在直二面角ABDC中,△ABD,△CBD均是以BD为斜边的等腰直角三角形,取AD的中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )
A.BC与平面A1BE内某直线平行
B.CD∥平面A1BE
C.BC与平面A1BE内某直线垂直
D.BC⊥A1B
12.(2020·聊城一模)如图,圆柱的轴截面ABCD为正方形,E为弧eq \(BC,\s\up10(︵))的中点,则异面直线AE与BC所成角的余弦值为( )
A.eq \f(\r(3),3) B.eq \f(\r(5),5)
C.eq \f(\r(30),6) D.eq \f(\r(6),6)二、填空题
1.如图所示,在空间四边形ABCD中,点E,H分别是边AB,AD的中点,点F,G分别是边BC,CD上的点,且eq \f(CF,CB)=eq \f(CG,CD)=eq \f(2,3),则下列说法正确的是________.
①EF与GH平行;
②EF与GH异面;
③EF与GH的交点M可能在直线AC上,也可能不在直线AC上;
④EF与GH的交点M一定在直线AC上.
2.一正方体的平面展开图如图所示,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60°;
③BD∥MN;
④BG与平面ABCD所成的角为45°.
其中正确的是________(填序号).
3.(2020·河南安阳调研四)在正方体ABCDA1B1C1D1中,点E∈平面AA1B1B,点F是线段AA1的中点,若D1E⊥CF,则当△EBC的面积取得最小值时,eq \f(S△EBC,S四边形ABCD)=________.
4.如图,已知正方体ABCDA1B1C1D1的棱长为2,长为2的线段MN的一个端点M在棱DD1上运动,点N在正方体的底面ABCD内运动,则MN的中点P的轨迹的面积是________.
5.(2020·西安模拟)如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,①GH与EF平行;②BD与MN为异面直线;③GH与MN成60°角;④DE与MN垂直.以上四个命题中,正确命题的序号是________.
6.如图,E,F分别是三棱锥PABC的棱AP,BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为________.
三 解答题
1.如图所示,在正方体ABCDA1B1C1D1中,E、F分别是AB和AA1的中点.求证:
(1)E,C,D1,F四点共面;
(2)CE,D1F,DA三线共点.
2.如图,在三棱锥PABC中,PA⊥底面ABC,D是PC的中点.已知∠BAC=eq \f(π,2),AB=2,AC=2eq \r(3),PA=2.求:
(1)三棱锥PABC的体积;
(2)异面直线BC与AD所成角的余弦值.
3.已知三棱柱ABCA1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面三角形ABC的中心,如图所示.
(1)连接BC1,求异面直线AA1与BC1所成角的大小;
(2)连接A1C,A1B,求三棱锥C1BCA1的体积.
4.(2020·衡阳模拟)如图,四棱锥MABCD中,∠CDA=∠DAB=90°,AB=2DC,△MCD与△MAD都是等边三角形,且点M在底而ABCD上的射影为O.
(1)证明:O为AC的中点;
(2)求异面直线MD与BC所成角的大小.
位置关系
图形表示
符号表示
公共点
直线a在平面α内
a⊂α
有无数个公共点
直线在平面外
直线a与平面α平行
a∥α
没有公共点
直线a与平面α斜交
a∩α=A
有且只有一个公共点
直线a与平面α垂直
a⊥α
位置关系
图形表示
符号表示
公共点
两平面平行
α∥β
没有
公共点两平面相交
斜交
α∩β=l
有一条公共直线
垂直
α⊥β且
α∩β=a
专题9.8 曲线与方程-2022年高考数学(理)一轮复习-题型全归纳与高效训练突破学案: 这是一份专题9.8 曲线与方程-2022年高考数学(理)一轮复习-题型全归纳与高效训练突破学案,文件包含专题98曲线与方程解析版docx、专题98曲线与方程原卷版docx等2份学案配套教学资源,其中学案共33页, 欢迎下载使用。
专题5.3 平面向量的数量积及应用-2022年高考数学(理)一轮复习-题型全归纳与高效训练突破学案: 这是一份专题5.3 平面向量的数量积及应用-2022年高考数学(理)一轮复习-题型全归纳与高效训练突破学案,文件包含专题53平面向量的数量积及应用解析版docx、专题53平面向量的数量积及应用原卷版docx等2份学案配套教学资源,其中学案共35页, 欢迎下载使用。
专题5.1 平面向量的概念及线性运算-2022年高考数学(理)一轮复习-题型全归纳与高效训练突破学案: 这是一份专题5.1 平面向量的概念及线性运算-2022年高考数学(理)一轮复习-题型全归纳与高效训练突破学案,文件包含专题51平面向量的概念及线性运算解析版docx、专题51平面向量的概念及线性运算原卷版docx等2份学案配套教学资源,其中学案共33页, 欢迎下载使用。












