2022滁州定远县育才学校高一下学期第一次月考数学试题含答案

这是一份2022滁州定远县育才学校高一下学期第一次月考数学试题含答案，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
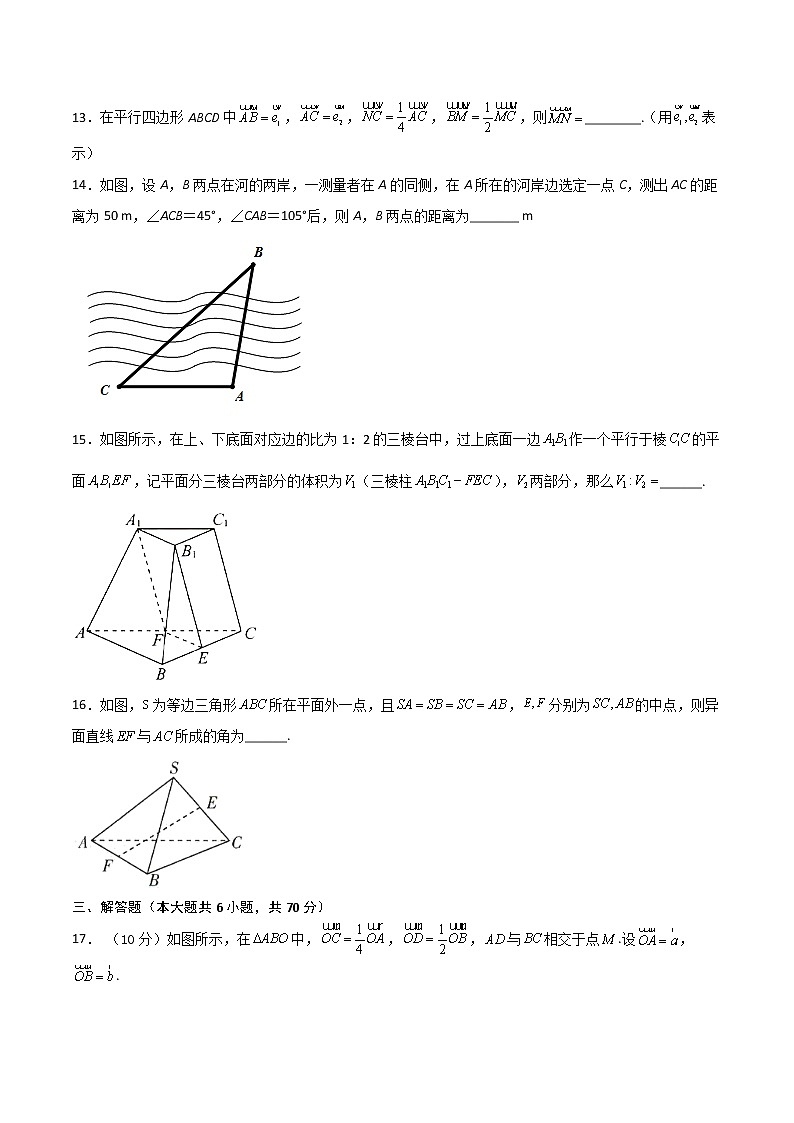
2021-2022学年度第二学期第一次月考试卷高一数学试题（考试时间：120分钟，满分：150分）一、选择题（本大题共12小题，共60分）1． （       ）A． B． C． D．2．下列说法错误的是（       ）A．若非零向量有，，则 B．零向量与任意向量平行C．已知向量不共线，且，，则 D．平行四边形中，3．已知正方形的边长为6，在边上且，为的中点，则（       ）A．-6 B．12 C．6 D．-124．若向量，满足，且，则向量与的夹角为（       ）A． B． C． D．5．在中，，．若点满足，则（ ）A． B． C． D．6．已知是虚数单位，复数，则复数在复平面内表示的点位于A．第一象限 B．第二象限 C．第三象限 D．第四象限7．如图所示，隔河可以看到对岸两目标A，B，但不能到达，现在岸边取相距4km的C，D两点，测得∠ACB＝75°，∠BCD＝45°，∠ADC＝30°，∠ADB＝45°(A，B，C，D在同一平面内)，则两目标A，B间的距离为（       ）km.A． B． C． D．28．欧拉公式（为虚数单位）是由瑞士著名数学家欧拉发现的，他将指数函数的定义域扩大到复数集，建立了三角函数和指数函数的关系，它在复变函数理论中占有非常重要的地位，特别是当时，被称为数学上的优美公式.根据欧拉公式，表示复数，则（       ）A． B． C． D．9．三棱柱中，，，，，侧棱长为，则其侧面积为（       ）A． B． C． D．10．下列说法中正确的个数是（       ）①空间中三条直线交于一点，则这三条直线共面；②平行四边形可以确定一个平面；③若一个角的两边分别平行于另一个角的两边，则这两个角相等；④若，且，则在上.A．1 B．2 C．3 D．411．一个圆柱的侧面展开图是一个正方形，则这个圆柱的表面积与侧面积的比值是（       ）A． B． C． D．12．垂直于正方形所在平面，连接，，，，，则下列垂直关系正确的个数是（       ）①面面②面面③面面④面面A．1 B．2 C．3 D．4二、填空题（本大题共4小题，共20分）13．在平行四边形ABCD中，，，，则________.（用表示）14．如图，设A，B两点在河的两岸，一测量者在A的同侧，在A所在的河岸边选定一点C，测出AC的距离为50 m，∠ACB＝45°，∠CAB＝105°后，则A，B两点的距离为_______ m15．如图所示，在上、下底面对应边的比为1：2的三棱台中，过上底面一边作一个平行于棱的平面，记平面分三棱台两部分的体积为（三棱柱），两部分，那么______.16．如图，为等边三角形所在平面外一点，且，分别为的中点，则异面直线与所成的角为______.三、解答题（本大题共6小题，共70分）17． （10分）如图所示，在中，，，与相交于点.设，.（1）试用向量、表示；（2）在线段上取一点，在线段上取一点，使过点，设，，求证：.18．（12分）如图，一艘船从港口O出发往南偏东75°方向航行了100km到达港口A，然后往北偏东60°方向航行了160km到达港口B．试用向量分解知识求从出发点O到港口B的直线距离（，结果精确到）．（提示：将，分解为垂直的两个向量．）19．（12分）如图所示，圆形纸片的圆心为，半径为，该纸片上的等边三角形的中心为，点，，为圆上的点，分别是以为底边的等腰三角形，沿虚线剪开后，分别以为折痕折起，使得，，重合，得到三棱锥，则当的边长变化时，求三棱锥的表面积的取值范围.20．（12分）如图，长方体中，；(1)求异面直线和所成角的正切值；(2)求三棱柱的体积和表面积.21．（12分）如图，四边形中，，分别在上，.现将四边形沿折起，使得平面平面.（1）当时，是否在折叠后的上存在一点，使得平面？若存在，求出点位置；若不存在，说明理由（2）设，问当为何值时，三棱锥的体积有最大值？并求出这个最大值.22．（12分）如图，正方体中，，分别为，的中点．（1）求证：，，，四点共面；（2）若，，与平面交于点，求证：三点共线．
参考答案1．A 2．D3．A4．B5．A6．C7．B8．B9．C10．B11．B12．B13．14．15．3：416．45°17．【详解】（1）不妨设.由于、、三点共线，则存在使得，即，于是.又，所以，则，即.①由于、、三点共线，则存在使得，即，于是.又，所以，所以，即.②由①②可得，，所以；（2）由于、、三点共线，所以存在实数使得，即，于是.又，，所以，所以，则，可得，两式相加得.18．【详解】建立如图所示的坐标系：显然，于是有：，，，，所以，因为，所以有：19． 解：由题可知，等边三角形的中心为，圆的半径为6，设三棱锥的底面边长为，即等边三角形的边长为，如图，连接，交与点，由题意可知，，则，，可知，即，则，，则，三棱锥的底面积为：，由题可知，全等，则面积相等，三棱锥的侧面积为：，所以三棱锥的表面积为：，，，即，所以当的边长变化时，求三棱锥的表面积的取值范围是.20．【解析】 (1)在长方体中，因为，所以与所成的角即为与所成的角，即（或补角），，所以异面直线和所成角的正切值为；(2)易知三棱柱是直三棱柱，底面是直角三角形，所以．又为三棱柱的高，所以，又四边形为矩形，，所以，故所求表面积.21．【详解】（1）存在点，使得平面，此时.当时，，过点作，交于点，连接，如图，则.∵在四边形中，∴，∴.∵，∴，且，故四边形为平行四边形，∴.∵平面平面，∴平面.（2）∵平面平面，平面平面，平面.∵，∴，故三棱锥的体积，当时，三棱锥的体积有最大值，最大值为322． 证明：（1）连接，在正方体中，∵，分别为，的中点，∴是的中位线，∴，又因为，∴∴四边形为梯形，即，，，四点共面．（2）在正方体中，，，∴是平面与平面的交线，又因为交平面于点，∴是平面与平面的一个公共点．因为两平面相交的所有公共点都在这两个平面的交线上，∴三点共线．