
数学必修 第二册第八章 立体几何初步8.3 简单几何体的表面积与体积图片课件ppt
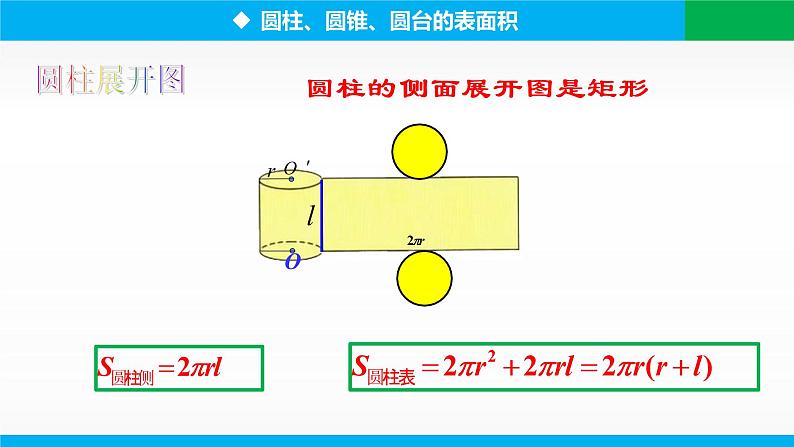
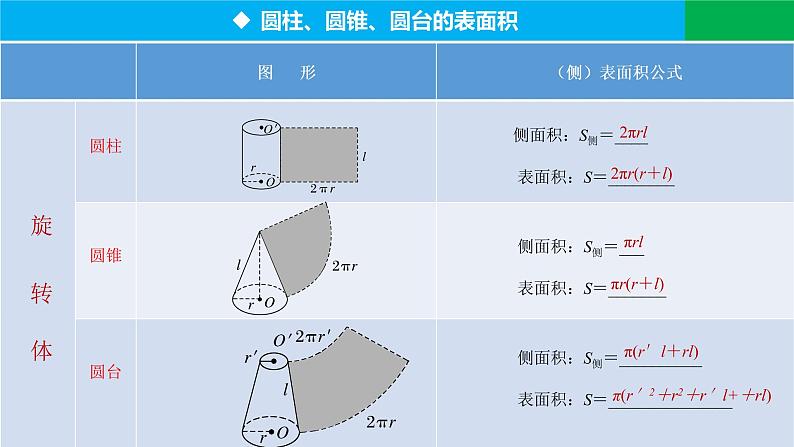
展开圆柱的侧面展开图是矩形
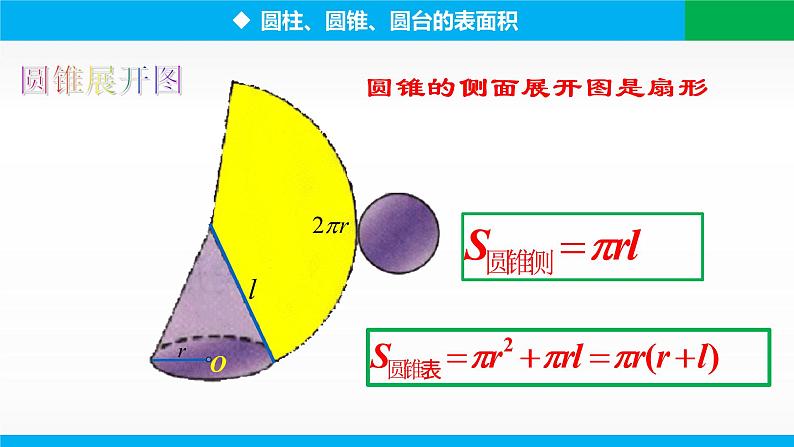
圆锥的侧面展开图是扇形
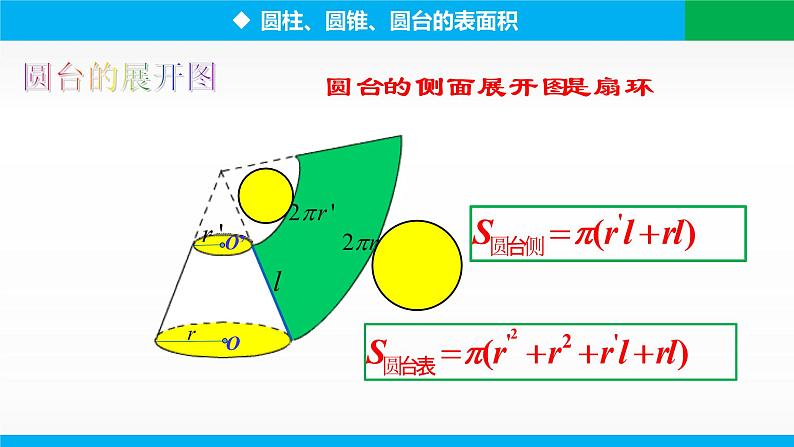
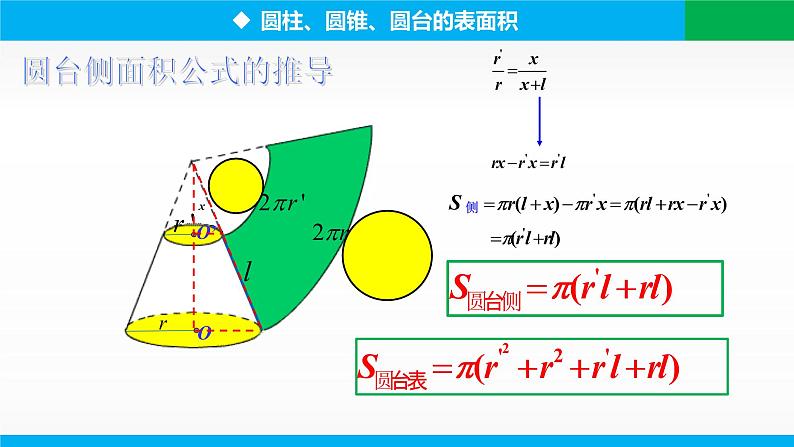
圆台的侧面展开图是扇环
侧面积:S侧=____
侧面积:S侧=__________
π(r′2+r2+r′l++rl)
表面积:S=_______
表面积:S=________
表面积:S=_______________
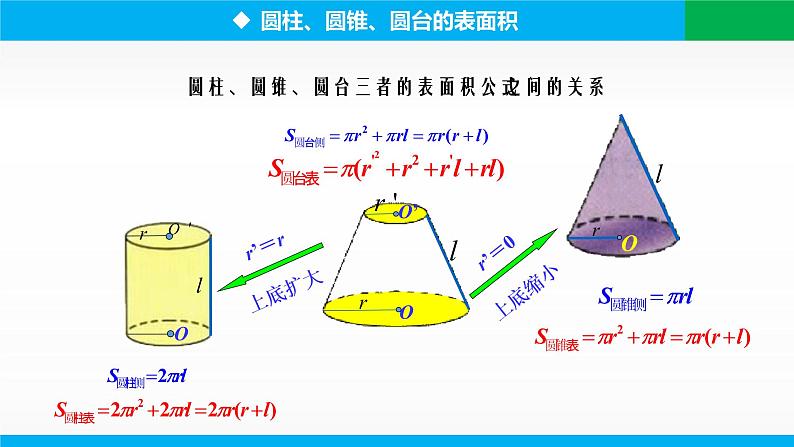
圆柱、圆锥、圆台三者的表面积公式之间的关系
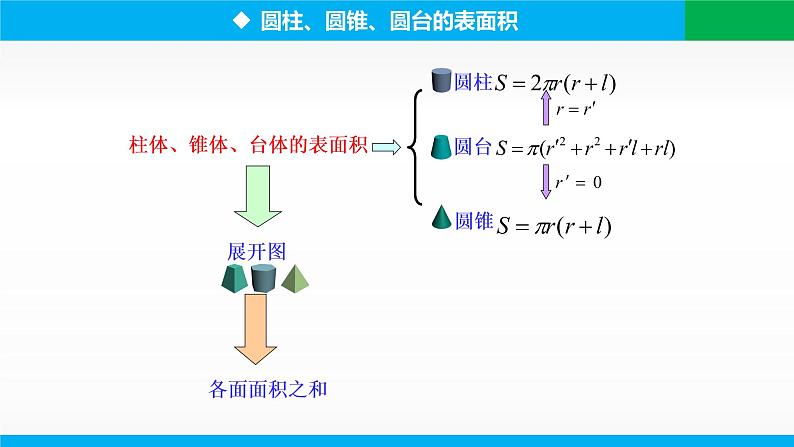
柱体、锥体、台体的表面积
例1 圆柱的一个底面积是S,侧面展开图是一个正方形,那么这个圆柱的侧面积是
解 设底面半径为r,则πr2=S,
又侧面展开图为一个正方形,
例2 若某圆锥的高等于其底面直径,则它的底面积与侧面积之比为
解 设圆锥底面半径为r,则高h=2r,
例3 已知某圆台的一个底面周长是另一个底面周长的3倍,母线长为3, 圆台的侧面积为84π,则该圆台较小底面的半径为 A.7 B.6 C.5 D.3
解 设圆台较小底面的半径为r, 则另一底面的半径为3r. 由S侧=3π(r+3r)=84π,解得r=7.
棱柱(圆柱)可由多边形(圆)沿某一方向得到,因此,两个底面积相等、高也相等的棱柱(圆柱)应该具有相等的体积.
圆台(棱台)是由圆锥(棱锥)截成的
柱体、锥体、台体的体积
__________________
例4 (多选)圆柱的侧面展开图是长12 cm,宽8 cm的矩形,则这个圆柱的 体积可能是
例5 已知圆台的上、下底面半径和高的比为1∶4∶4,母线长为10,则圆台的体积为________.
解 设上底面半径为r, 则下底面半径为4r,高为4r,如图. ∵母线长为10,∴102=(4r)2+(4r-r)2, 解得r=2. ∴下底面半径R=8,高h=8,
例6 圆锥的轴截面是等腰直角三角形,侧面积是 ,则圆锥的体积是
解 作圆锥的轴截面,如图所示, 由题意知,在△PAB中,∠APB=90°,PA=PB. 设圆锥的高为h,底面半径为r,
∴S球=4πR2=16π.
A.4π B.12π C.24π D.48π
∴S球=4πR2=12π.
解 正方体的棱长为a,其内切球的半径为R,则a=2R,
例10 将两个半径为1的小铁球熔化后铸成一个大球,则这个大球的半径R为______.
KE TANG XIAO JIE
1.知识点: (1)圆柱、圆锥、圆台的表面积. (2)圆柱、圆锥、圆台的体积. (3)球的表面积和体积. (4)组合体的表面积与体积.
2.方 法:公式法.
3.易错点:平面图形与立体图形的切换不清楚.
课本p119 练习 1、2、3、4
人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积多媒体教学课件ppt: 这是一份人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积多媒体教学课件ppt,共27页。PPT课件主要包含了复习引入,棱柱的体积,棱锥的体积,棱台的体积,1圆柱的表面积,2圆锥的表面积,3圆台的表面积,球的表面积,球的表面积及体积,圆锥圆台球等内容,欢迎下载使用。
人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积评优课课件ppt: 这是一份人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积评优课课件ppt,共26页。PPT课件主要包含了学习目标,新知学习,易错辨析,典例剖析,反思感悟,跟踪训练,球的表面积与体积,随堂小测,课堂小结等内容,欢迎下载使用。
人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积课文内容课件ppt: 这是一份人教A版 (2019)必修 第二册8.3 简单几何体的表面积与体积课文内容课件ppt,共39页。













