第13讲 空间图形的位置关系(分层训练)-2022年春季高一数学辅导讲义（苏教版2019必修第二册）

这是一份第13讲 空间图形的位置关系(分层训练)-2022年春季高一数学辅导讲义（苏教版2019必修第二册），文件包含第13讲空间图形的位置关系分层训练解析版docx、第13讲空间图形的位置关系分层训练原卷版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。

基础组
一、选择题
1．(2021•浙江二模)已知直线l，m和平面α( )
A．若l∥m，m⊂α，则l∥α；B．若l∥α，m⊂α，则l∥m；
C．若l⊥α，m⊂α，则l⊥m；D．若l⊥m，l⊥α，则m⊥α
【答案】C．
【解析】对于A，若l∥m，m⊂α，则l∥α或l⊂α，故A错误；
对于B，若l∥α，m⊂α，则l∥m或l与m异面，故B错误；
对于C，若l⊥α，m⊂α，则由线面垂直的性质得l⊥m，故C正确；
对于D，若l⊥m，l⊥α，则m与α平行或m⊂α，故D错误．
2．(2021春•瑶海区月考)如图所示，将无盖正方体纸盒展开，直线AB，CD在原正方体中的位置关系是( )
A．平行；B．相交；C．异面；D．相交成60°
【答案】D．
【解析】将无盖正方体纸盒还原后，A，B，C，D在正方体中的位置如图所示，
连结AC，则△ABC为等边三角形，
所以∠ABC＝60°，
所以直线AB，CD在原正方体中的位置关系是相交成60°．
3．(2021春•瑶海区月考)如图是一个正方体的展开图，如果将它还原为正方体，那么AB，CD，EF，GH这四条线段所在直线是异面直线的对数是( )
A．3；B．4；C．5；D．6
【答案】C．
【解析】如图所示，把展开图再还原成正方体，
由经过平面外一点和平面内一点的直线和平面内不经过该点的直线是异面直线，
可得AB，CD，EF，GH这四条线段所在直线是异面直线的有，AB和CD，AB和GH，CD和EF，CD和GH，EF和GH，共5对．
4．(2021•浙江模拟)已知平面α∥平面β，且直线l⊂α，直线m⊂β，则l与m的位置关系不可能是( )
A．平行；B．异面；C．相交；D．平行或异面
【答案】C．
【解析】因为平面α∥平面β，可得两平面α，β无公共点，即有直线l与直线m也无公共点，
所以直线l与直线m可能平行或异面，即不可能相交．
5．(2021•贵州模拟)如图，G，H，M，N分别是直三棱柱的顶点或所在棱的中点，则在下列图形中GH∥MN的是( )
A．；B．；C．；D．
【答案】D．
【解析】对于A，若GH∥MN，可得G，H，M，N四点共面，则直线MG，HN共面，
这与MG，NH异面矛盾，所以A中的两直线不平行；
由异面直线的定义可得B，C中的两直线GH，MN为异面直线；
由N，H为中点，可得NH∥MG，且NH＝MG，则四边形MGHN为平行四边形，
D中的两直线为平行直线．
6．(2021•合肥一模)我国古代数学名著《九章算术》第五卷“商功”中，把底面为直角三角形的直三棱柱称为堑堵．如图，在堑堵ABC﹣A1B1C1中，AC＝BC＝CC1，M，N分别是线段A1C，BC1上的点，且A1M＝2MC，BN＝2NC1，则下列说法正确的是( )
A．A1C⊥AB；B．A1C⊥BC1；C．MN⊥A1B；D．MN⊥A1C
【答案】D．
【解析】设AC＝BC＝CC1＝3，C1P=13C1C＝1，CQ=13CC1＝1，PQ＝1，
由A1M＝2MC，BN＝2NC1，可得CM=13A1C=13×32=2，
又PN∥CB，PN⊥CC1，可得CN=CP2+PN2=4+1=5，
由BC⊥AC，BC⊥CC1，可得BC⊥平面ACC1A1，
则NP⊥平面ACC1A1，NP⊥PM，
又MQ⊥CQ，
所以MN=MQ2+PQ2+NP2=1+1+1=3，
所以CM2+MN2＝CN2，
所以MN⊥A1C，
故D正确．
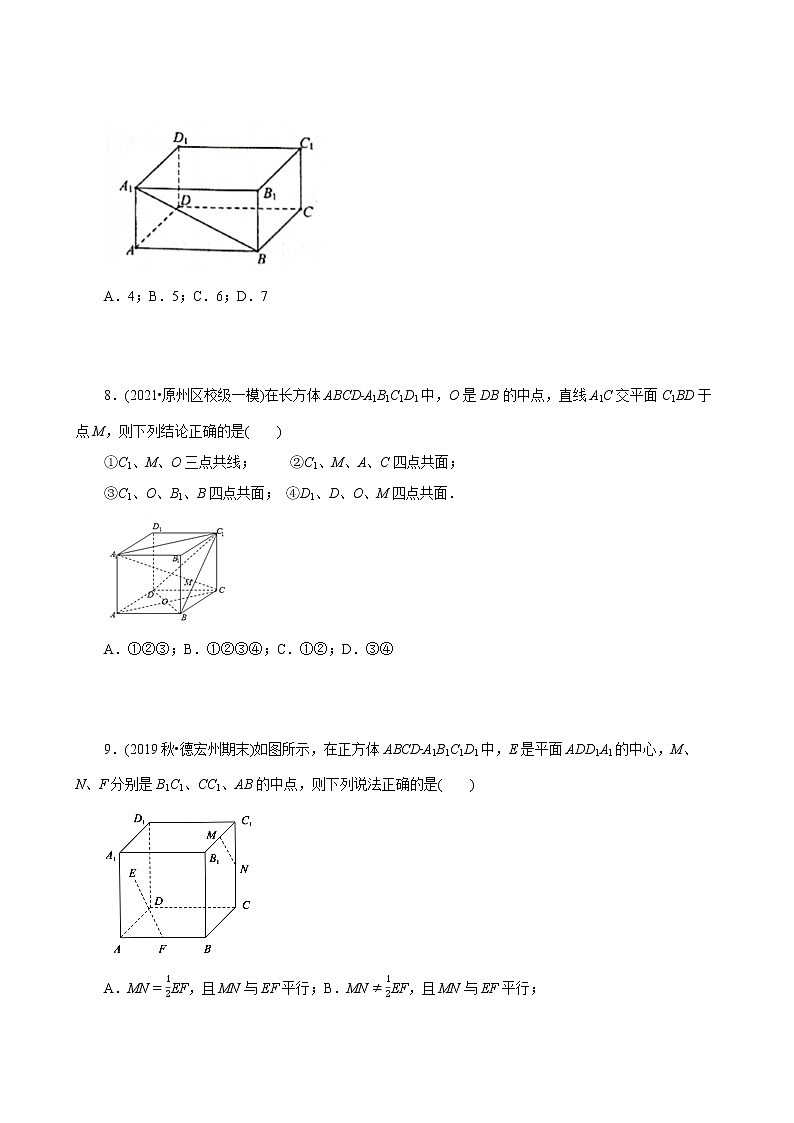
7．(2020秋•泸州期末)如图，长方体ABCD﹣A1B1C1D1的棱所在直线与直线BA1为异面直线的条数是( )
A．4；B．5；C．6；D．7
【答案】C．
【解析】根据异面直线的定义可得，与直线BA1为异面直线的棱有：AD，B1C1，CD，C1D1，CC1，DD1，共6条．
8．(2021•原州区校级一模)在长方体ABCD﹣A1B1C1D1中，O是DB的中点，直线A1C交平面C1BD于点M，则下列结论正确的是( )
①C1、M、O三点共线； ②C1、M、A、C四点共面；
③C1、O、B1、B四点共面； ④D1、D、O、M四点共面．
A．①②③；B．①②③④；C．①②；D．③④
【答案】C．
【解析】∵O∈AC，AC⊂平面ACC1A1，∴O∈平面ACC1A1，∵O∈BD，BD⊂平面C1BD，∴O∈平面C1BD，∴O是平面ACC1A1和平面C1BD的公共点；
同理可得，点M和C1都是平面ACC1A1和平面C1BD的公共点，所以根据公理3可得C1、B，D在平面ACC1A1和平面C1BD的交线上，因此①正确．
∵AA1∥BB1，BB1∥CC1，∴AA1∥CC1∴AA1，CC1确定一个平面，又M∈A1C，A1C⊂平面ACC1A1，∴M∈平面ACC1A1，故②正确．
根据异面直线的判定定理可得BB1与C1O为异面直线，故C1、O、B1、B四点不共面，故③不正确．
根据异面直线的判定定理可得DD1与MO为异面直线，故D1、D、O、M四点不共面，故④不正确．
9．(2019秋•德宏州期末)如图所示，在正方体ABCD﹣A1B1C1D1中，E是平面ADD1A1的中心，M、N、F分别是B1C1、CC1、AB的中点，则下列说法正确的是( )
A．MN=12EF，且MN与EF平行；B．MN≠12EF，且MN与EF平行；
C．MN=12EF，且MN与EF异面；D．MN≠12EF，且MN与EF异面
【答案】D．
【解析】设正方体ABCD﹣A1B1C1D1的棱长为2a，
则MN=MC12+C1N2=(2a2)2+(2a2)2=2a，
作点E在平面ABCD内的射影点G，连结EG，GF，
所以EF=EG2+GF2=(2a2)2+(2a)2=3a，
所以MN≠12EF，故选项A，C错误；
连结DE，因为E为平面ADD1A1的中心，所以DE=12A1D，
又因为M，N分别为B1C1，CC1的中点，所以MN∥B1C，
又因为B1C∥A1D，所以MN∥ED，且DE∩EF＝E，
所以MN与EF异面，故选项B错误．
10．(2020•德阳模拟)如图，△ABC是等腰直角三角形，AB＝AC，在△BCD中∠BCD＝90°且BC＝3．将△ABC沿BC边翻折，设点A在平面BCD上的射影为点M，若AM=32，那么( )
A．平面ABD⊥平面BCD；B．平面ABC⊥平面ABD；C．AB⊥CD；D．AC⊥BD
【答案】C
【解析】△ABC是等腰直角三角形，AB＝AC，BC＝3，
点A在平面BCD上的射影为点M，若AM=32，
由AM=12BC，可得M为BC的中点，
AM⊥平面BCD，则AM⊥CD，
又CD⊥BC，AM，BC为相交直线，
可得CD⊥平面ABC，可得CD⊥AB，
11．(2020•兴庆区校级四模)在空间中，a、b、c是三条不同的直线，α、β是两个不同的平面，则下列命题中的真命题是( )
A．若a⊥c，b⊥c，则a∥b；B．若a⊂α，b⊂β，α⊥β，则a⊥b；
C．若a∥α，b∥β，α∥β，则a∥b；D．若α∥β，a⊂α，则a∥β
【答案】D．
【解析】对于A，若a⊥c，b⊥c，则a∥b或a与b相交或a与b异面，故A错误；
对于B，若a⊂α，b⊂β，α⊥β，则a∥b或a与b相交或a与b异面，故B错误；
对于C，若a∥α，b∥β，α∥β，则a∥b或a与b异面，故C错误；
对于D，若α∥β，a⊂α，则a∥β，故D正确．
12．(2020•运城模拟)已知m，n是空间中两条不同的直线，α，β是两个不同的平面，现有如下命题：
①若m∥α，n∥β，m∥n，则α∥β；②若m⊥α，n⊥β，m∥n，则α∥β；
③若α∥β，m⊂α，n⊂β，则m∥n；④若m∥α，m∥n，n⊥β，则α⊥β，
则正确命题的个数为( )
A．4；B．3；C．2；D．1
【答案】C．
【解析】①中，若m∥α，n∥β，m∥n，则α∥β或α与β相交，故①错误；
②中，若m⊥α，m∥n，则n⊥α，又n⊥β，则α∥β，故②正确；
③中，若α∥β，m⊂α，n⊂β，则m∥n或m与n异面，故③错误；
④中，若m∥α，m∥n，则n∥α或n⊂α，又n⊥β，则α⊥β，故④正确．
∴正确命题的个数为2个．
二、解答题
13．(2020秋•潍坊期中)从①BG→=2GC→，②G是PB的中点，③G是△PBC的内心三个条件中任选一个条件，补充在下面问题中，并完成解答，在四棱锥P﹣ABCD中，底面ABCD是矩形，PD⊥底面ABCD，且PD＝1，AB=3，AD＝2，E，F分别为PC，BD的中点．
(1)判断EF与平面PAD的位置关系，并证明你的结论；
【解析】解：(1)EF与平面PAD平行．
证明如下：
连接AC，则AC与BD交于F点，
在△PAC中，E，F均为中点，∴EF∥PA，
∵EF⊄平面PAD，PA⊂平面PAD，
∴EF∥平面PAD．
14．(2020秋•南康区校级月考)在立体几何中，用一个平面去截一个几何体得到的平面图形叫截面．如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，点G，M分别是棱C1C，BC的中点．
(1)证明：A、M、G、D1共面；
【解析】解：(1)证明：连结BC1，
在正方体中，∵D1C1∥AB，∴BC1∥AD1，
又∵BC1∥GM，∴AD1∥MG，
∴A、M、G、D1四点共面．
15．(2020•武汉模拟)如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，PD＝2，DC＝BC＝1，AB＝2，AB∥DC，∠BCD＝90°．
(1)求证：AD⊥PB；
【解析】解：(1)如图所示，
在四边形ABCD中，连接BD，由DC＝BC＝1，AB＝2，∠BCD＝∠ABC=π2，
在△ABD中，BD＝AD=2，又AB＝2，
因此AD⊥BD，又PD⊥平面ABCD，
∴PD⊥AD，又BD∩PD＝D，
∴AD⊥平面PBD，
∴AD⊥PB；
16．(2020•锡山区校级模拟)如图，已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直，∠BAC＝90°，M，N分别是A1B1，BC的中点．
(Ⅰ)证明：AB⊥AC1；
【解析】证明：(Ⅰ)由题意知，CC1⊥平面ABC，
∵AB⊂平面ABC，∴CC1⊥AB．
∵∠BAC＝90°，即AC⊥AB，且AC∩CC1＝C，
∴AB⊥平面ACC1A1．
又∵AC1⊂平面ACC1A1，∴AB⊥AC1．
17．(2019春•孝感期中)在四面体ABCD中，E，H分别是线段AB，AD的中点，F，G分别是线段CB，CD上的点，且CFBF=CGDG=12．求证：
(1)四边形EFGH是梯形；
【解析】证明：(1)连结BD，
∵E，H分别是边AB，AD的中点，
∴EH∥BD，且EH=12BD，
又∵CFCB=CGCD=13，
∴FG∥BD，且FG=13BD，
因此EH∥FG且EH≠FG
故四边形EFGH是梯形．
18．(2018秋•鄂州期中)如图1，在直角△ABC中，∠ABC＝90°，AC＝43，AB＝23，D，E分别为AC，BD的中点，连结AE并延长交BC于点F，将△ABD沿BD折起，使平面ABD⊥平面BCD，如图2所示．
(Ⅰ)求证：AE⊥CD；
【解析】(Ⅰ)如图所示：
证明：由条件可知AB＝AD，E为BD的中点，
所以：AE⊥BD，
又面ABD⊥面BDC，
面ABD∩面BCD＝BD，且AE⊂面ABD，
所以：AE⊥面BCD
又因为CD⊂平面BCD，
所以：AE⊥CD．
19．(2021•安徽模拟)如图，在四棱锥P﹣ABCD中，AB∥CD，AB⊥平面PAD，PA＝AD＝DC＝2AB＝4，PD＝27，M是PC的中点．
(1)证明：平面ABM⊥平面PCD；
【解析】(1)证明：取PD的中点N，连接MN，AN，
∵PA＝AD，∴AN⊥PD，
∵AB∥CD，AB⊥平面PAD，
∴CD⊥平面PAD，∴CD⊥AN，
又PD∩CD＝D，PD、CD⊂平面PCD，
∴AN⊥平面PCD，
∵AN⊂平面ABM，
∴平面ABM⊥平面PCD．
提高组
一、选择题
1．(2020秋•玉溪月考)已知正方体ABCD﹣A1B1C1D1的棱长为3，E，F，G分别为棱AA1，AB，CC1上的点，其中AE＝1，AF＝2，CG=32，平面α经过点E，F，G，则α截此正方体所得的截面为( )
A．三角形；B．四边形；C．五边形；D．六边形
【答案】C．
【解析】根据两平行平面被第三个平面所截的交线平行，可知截面α与平面CC1D1D的交线平行于EF，
取AA1的中点N，BB1的中点M，连结BN、A1M、MG，
又AE＝1，AF＝2，AN=32，AB＝3，
所以EF∥BN，而BN∥A1M，A1M∥D1G，
所以EF∥D1G，D1G即为截面α与平面CC1D1D的交线，
而D1∈α，E∈α，D1∈平面ADD1A1，E∈平面ADD1A1，所以α∩平面ADD1A1＝ED1，
同理在BC上取点H，使得CH=94，ED1∥HG，连结FH，
所以平面EFHGD1即为截面α，即α截此正方体所得的截面为五边形．
2．(2020秋•富顺县校级期中)a、b、c是三条不重合的直线，下列说法正确的是( )
A．若a∥b，b∥c，则a∥c；B．若a⊥b，a⊥c，则b⊥c；
C．若直线l1，l2没有交点，则l1，l2异面；D．若a⊥b，a⊥c，则b∥c
【答案】A．
【解析】a、b、c是三条不重合的直线，
对于A，若a∥b，b∥c，则由平行公理得a∥c，故A正确；
对于B，若a⊥b，a⊥c，则b与c相交、平行或异面，故B错误；
对于C，若直线l1，l2没有交点，则l1，l2异面或平行，故C错误；
对于D，若a⊥b，a⊥c，则b与c平行、相交或异面，故D错误．
3．(2020秋•怀仁市期中)设m，n是两条不同的直线，α表示平面，下列说法正确的是( )
A．若m∥α，n⊂α，则m∥n；B．若m∥α，m⊥n，则n⊥α；
C．若m⊥α，m⊥n，则n∥α；D．若m⊥α，n∥α，则m⊥n
【答案】D．
【解析】由m，n是两条不同的直线，α表示平面，
对于A，若m∥α，n⊂α，则m与n平行或异面，故A错误；
对于B，若m∥α，m⊥n，则n与α相交、平行或n⊂α，故B错误；
对于C，若m⊥α，m⊥n，则n∥α或n⊂α，故C错误；
对于D，若m⊥α，n∥α，
则由线面垂直的性质和线面平行的性质得m⊥n，故D正确．
4．(2020秋•瑶海区校级期中)若直线l与平面α平行，直线a⊂α，则l与a位置关系( )
A．平行；B．异面；C．相交；D．没有公共点
【答案】D．
【解析】∵直线l与平面α平行，∴l与平面α没有公共点，
又直线a⊂α，∴l与a没有公共点，故C错误，D正确；
直线l与直线a没有公共点，则l与a可能平行，也可能异面，故A与B错误．
5．(2020秋•汾阳市期中)关于空间两条直线a，b和平面α，下列命题正确的是( )
A．若a∥α，b∥α，则a∥b；B．若a⊥α，b⊥α，则a∥b；
C．若a∥b，b∥α，则a∥α；D．若a⊥b，b⊥α，则a∥α
【答案】B．
【解析】若a∥α，b∥α，则a∥b或a与b相交或a与b异面，故A错误；
若a⊥α，b⊥α，由直线与平面垂直的性质可得a∥b，故B正确；
若a∥b，b∥α，则a∥α或a⊂α，故C错误；
若a⊥b，b⊥α，则a∥α或a⊂α，故D错误．
6．(2020秋•资中县校级期中)若l1、l2为异面直线，直线l3与l2平行，则l1与l3的位置关系是( )
A．相交；B．异面；C．平行；D．异面或相交
【答案】D．
【解析】在正方体ABCD﹣A1B1C1D1中，
AB和CC1是异面直线，DD1∥CC1，AB和DD1是异面直线；
AB和CC1是异面直线，BB1∥CC1，AB和BB1是相交直线，
∴若l1、l2为异面直线，直线l3与l2平行，
则l1与l3的位置关系是异面或相交．
7．(2020秋•成都期中)若直线a⊥平面α，直线b⊥平面α，则直线a与直线b的位置关系为( )
A．异面；B．相交；C．平行；D．平行或异面
【答案】C．
【解析】若直线a⊥平面α，直线b⊥平面α，则直线a与直线b的位置关系是平行．
原因如下：
若a与b相交，设交点为O，则过O点有两条直线都有平面α垂直，与过一点有且只有一条直线与已知平面垂直矛盾；
若a与b异面，如图，
设b∩α＝O，则由a与O可确定平面β，在β内过O作直线c∥a，则c⊥α，这样，过O有两条直线b与c与α垂直，
也与过一点有且只有一条直线与已知平面垂直矛盾．
8．(2020•碑林区校级模拟)已知在一个棱长为12的正方体ABCD﹣A1B1C1D1中，BB1和C1D1的中点分别为M，N，如图，则过A，M，N三点的平面被正方体所截得的截面图形为( )
A．六边形；B．五边形；C．四边形；D．三角形
【答案】B．
【解析】在一个棱长为12的正方体ABCD﹣A1B1C1D1中，BB1和C1D1的中点分别为M，N，
如图，截面与B1C1交于点E，且点E不会为B1或C1点，
截面与DD1交于F点，且点F不会为D或D1点，
∴截面有AM，ME，EN，NF，FA共计5条边，
∴过A，M，N三点的平面被正方体所截得的截面图形为五边形AMENF．
9．(2020•道里区校级模拟)正方体ABCD﹣A1B1C1D1的棱长为2，E是棱B1C1的中点，则平面AD1E截该正方体所得的截面面积为( )
A．42；B．22；C．4；D．92
【答案】D．
【解析】取BB1中点F，连结EF、AF，
则EF∥AD1，∴梯形AFED1是平面AD1E截该正方体所得的截面，
∵正方体ABCD﹣A1B1C1D1的棱长为2，E是棱B1C1的中点，
∴AD1=4+4=22，EF=12AD1=2，
AF＝D1E=4+1=5，
梯形AFED1的高h=(5)2-(22)2=322，
∴平面AD1E截该正方体所得的截面面积为：
S=12(22+2)×322=92．
10．(2020•东湖区校级模拟)在棱长为2的正方体ABCD﹣A1B1C1D1中，E是正方形BB1C1C的中心，M为C1D1的中点，过A1M的平面α与直线DE垂直，则平面α截正方体ABCD﹣A1B1C1D1所得的截面面积为( )
A．23；B．26；C．225；D．3
【答案】B．
【解析】如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，记AB的中点为N，
连结MC，CN，NA1，则平面A1MCN即为平面α，
证明如下：
由正方体的性质可知：A1M∥NC，则A1，M，C，N四点共面，
记CC1的中点为F，连结DF，由题意得DF⊥MC，连结EF，则EF⊥MC，
∴MC⊥平面DEF，则DE⊥MC，
同理可证DE⊥NC，NC∩MC＝C，∴DE⊥平面A1MCN，
∴平面A1MCN即平面α，且四边形A1MCN即平面α截正方体ABCD﹣A1B1C1D1所得截面，
∵正方体的棱长为2，由题意知四边形A1MCN是菱形，
其对角线A1C＝23，MN＝22，
∴平面α截正方体ABCD﹣A1B1C1D1所得的截面面积为：
S=12×22×23=26．
11．(2020春•清江浦区校级期中)如图，在空间四边形ABCD中，E、F、G、H分别是四边上的中点，则直线EG和FH的位置关系是( )
A．平行；B．相交；C．异面；D．以上都可能
【答案】A．
【解析】如图，
连接EF、EG、GH、FH，
∵E、G分别为AB、BC的中点，∴EG为△ABC的中位线，
则EG∥AC；
∵F、H分别为AD、DC的中点，∴FH为△ADC的中位线，
则FH∥AC．
由平行公理可得，EG∥FH．
12．(2020春•浙江期中)对于空间中的两条不同直线m，n和一个平面α，下列命题正确的是( )
A．若m∥α，n∥α，则m∥n；B．若m∥α，m∥n，则n∥α；
C．若m∥n，n⊂α，则m∥α；D．若m⊥α，n⊥α，则m∥n
【答案】D．
【解析】对于A，若m∥α，n∥α，可得m，n平行、相交或异面，故A错误；
对于B，若m∥α，m∥n，则n∥α或n⊂α，故B错误；
对于C，若m∥n，n⊂α，且m⊄α，则m∥α，故C错误；
对于D，若m⊥α，n⊥α，由同垂直于题意平面的两直线平行，可得m∥n，故D正确．
13．(2020春•龙凤区校级期中)在空间中，已知m，n为不同的直线，α，β，γ为不同的平面，则下列判断正确的是( )
A．若m⊂α，m∥n，则n∥α；B．若m⊥α且m∥β，则α⊥β；
C．若l⊥m，l⊥n，m⊂α，n⊂α，则l⊥α；D．若α⊥β，α⊥γ，则β∥γ
【答案】B．
【解析】由m，n为不同的直线，α，β，γ为不同的平面，知：
对于A，若m⊂α，m∥n，则n∥α或n⊂α，故A错误；
对于B，若m⊥α且m∥β，则由面面垂直的判定定理得α⊥β，故B正确；
对于C，若l⊥m，l⊥n，m⊂α，n⊂α，则l与α相交、平行或l⊂α，故C错误；
对于D，若α⊥β，α⊥γ，则β与γ相交或平行，故D错误．
二、解答题
14．(2021•安庆模拟)如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的菱形，∠DAB＝60°，PB＝PD=7，PA＝3．
(1)证明：PA⊥BD；
【解析】(1)证明：连接AC交BD于点O，∵底面ABCD为菱形，
∴BD⊥AC，OB＝OD，
又∵PB＝PD，∴BD⊥PO，而AC∩PO＝O，
∴BD⊥平面PAC，
又∵PA⊂平面PAC，∴PA⊥BD；
15．(2021•黄山二模)如图，在长方体ABCD﹣A1B1C1D1中，AB＝4，AD＝AA1＝2，E是CD的中点，F是底面A1B1C1D1上的动点，且满足AF⊥BE．
(1)求证：平面AEF⊥平面ABCD；
【解析】(1)证明：∵AE=BE=22，AB=4，
∴AE2+BE2＝AB2，∴BE⊥AF，
又∵BE⊥AF，AE∩AF＝A，∴BE⊥平面AEF，…………………………(3分)
又∵BE⊂平面ABCD，∴平面AEF⊥平面ABCD；………………………………(5分)
16．(2021•兴庆区校级一模)如图，在直角梯形PBCD中，PD∥BC，∠DCB＝90°，PD＝4CD＝8，BA⊥PD，A为PD中点，现将平面图形沿AB折成一个直二面角，得到四棱锥P﹣ABCD，E，F分别为侧棱PD、PB的中点．
(1)证明：平面AEF⊥平面PCD；
【解析】解：(1)证明：∵PA＝AD，E是PD中点，∴AE⊥PD，
∵AB⊥AD，AB⊥PA，AB∩PA＝A，AB，PA⊂平面PAD，
∴AB⊥平面PAD，∵CD∥AB，∴CD⊥平面PAD，
∵AE⊂平面PAD，∴CD⊥AE，
∵CD∩PD＝D，CD、PD⊂平面PCD，
∴AE⊥平面PCD，
∵AE⊂平面AEF，∴平面AEF⊥平面PCD．
17．(2021•南充模拟)如图，在Rt△AOB中，AO＝OB＝2，△AOC通过△AOB以OA为轴顺时针旋转120°得到(∠BOC＝120°)．点D为斜边AB上一点，点M为线段BC上一点，且CM＝OM．
(1)证明：OM⊥平面AOB；
【解析】(1)证明：在△OBC中，由题意可得OB＝OC，∠OCB＝30°，
∵CM＝OM，∴∠COM＝∠OCM＝30°，
又∵∠BOC＝120°，∴OM⊥OB，
根据题意，OA⊥OB，OA⊥OC，OB∩OC＝O，∴OA⊥平面OBC，
而OM⊂平面OBC，∴OA⊥OM，
又OA∩OB＝O，∴OM⊥平面AOB；
18．(2021•山东二模)如图，在四棱锥S﹣ABCD中，四边形ABCD是边长为2的菱形，∠ABC＝60°，∠ASD＝90°，AS＝SD且SC＝2．
(1)证明：平面SAD⊥平面ABCD；
【解析】解：(1)证明：如图，取AD的中点O，连接SO、CO、AC，
∵∠ADC＝∠ABC＝60°，且AD＝DC，
又AD＝CD＝2，则△ACD为正三角形，∴CO⊥AD，CO=3，
又∵∠ASD＝90°，∴△ASD为直角三角形，∴SO=12AD=1，
在△ACS中，CO2+SO2＝SC2，则CO⊥SO，
又AD∩SO＝O，AD、SO⊂平面ADS，
∴CO⊥平面ADS，
又∵CO⊂平面ABCD，∴平面SAD⊥平面ABCD．
19．(2021•靖远县模拟)如图，在四棱锥P﹣ABCD中，平面ABCD⊥平面PAB，△PAB为等边三角形，四边形ABCD为矩形，E为PB的中点．
(1)证明：平面ADE⊥平面PBC；
【解析】(1)证明：∵△PAB为等边三角形，E为PB的中点，∴AE⊥PB，
∵平面ABCD⊥平面PAB，且平面ABCD∩平面PAB＝AB，AD⊥AB，
∴AD⊥平面PAB，则AD⊥PB，
又AD∩AE＝A，∴PB⊥平面ADE，
∵PB⊂平面PBC，∴平面ADE⊥平面PBC；
20．(2021•四川模拟)如图所示，几何体ABCDEFG中，四边形ABCD为菱形，ED⊥平面ABCD，FA∥GC∥ED，FA＝GC=13ED，FG＝2，BE＝4，平面BFG与平面ABCD的交线为l．
(1)证明：直线l⊥平面BDE；
【解析】(1)证明：如图，连接AC与BD交于点O，
由条件可知GC∥FA且GC＝FA，
所以四边形ACGF为平行四边形，所以AC∥FG，
因为FG⊂平面BFG，AC⊄平面BFG，所以AC∥平面BFG，
因为平面BFG与平面ABCD的交线为l，所以AC∥l，
因为ED⊥平面ABCD，所以ED⊥AC，
又因为四边形ABCD为菱形，所以AC⊥BD，
又因为BD∩DE＝D，
所以AC⊥平面BDE，
所以直线l⊥平面BDE．
21．(2021•长安区一模)如图，四棱锥P﹣ABCD中，PA⊥平面ABCD，AB⊥AD，AB∥CD，PD＝AB＝2AD＝2CD＝2，E为PA上一点，且3PE＝2PA．
(Ⅰ)证明：平面EBC⊥平面PAC；
【解析】(Ⅰ)证明：∵PA⊥平面ABCD，BC⊂平面ABCD，∴PA⊥BC，
∵在直角梯形ABCD中，AB∥CD，AB⊥AD，AB＝2，AD＝CD＝1，
∴AC=BC=2，∴AC2+BC2＝AB2，
∴AC⊥BC，
又PA∩AC，PA⊂平面PAC，
AC⊂平面PAC，
∴BC⊥平面PAC，
∵BC⊂平面EBC，∴平面EBC⊥平面PAC．
附：分层训练答案
基础组
1．C；2．D；3．C；4．C；5．D；6．D；7．C；8．C；9．D；10．C11；D．12；C．
提高组
1．C；2．A；3．D；4．D；5．B；6．D；7．C；8．B；9．D；10．B；11．A；12．D；13．B．