方法技巧专题01 数列求和问题-2022年高考数学满分之路方法技巧篇

这是一份方法技巧专题01 数列求和问题-2022年高考数学满分之路方法技巧篇，文件包含方法技巧专题01数列求和问题解析版docx、方法技巧专题01数列求和问题原卷版docx等2份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。
 方法技巧专题1 数列求和问题 解析版



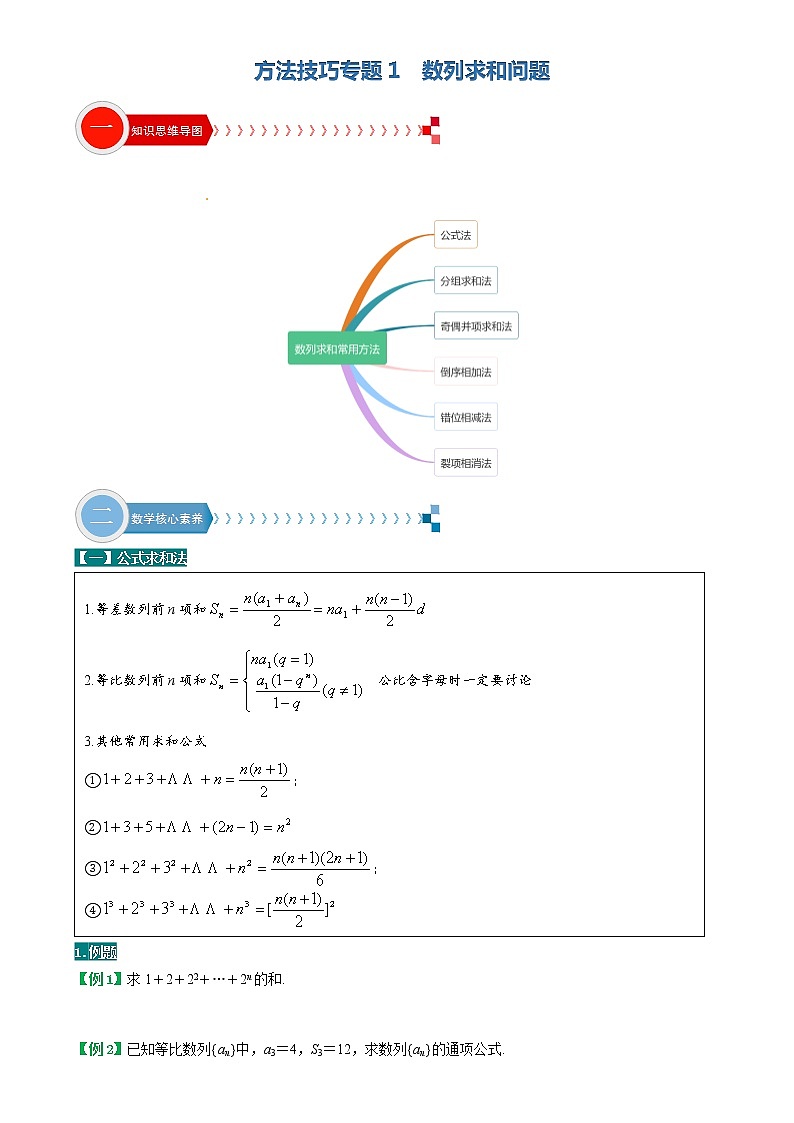
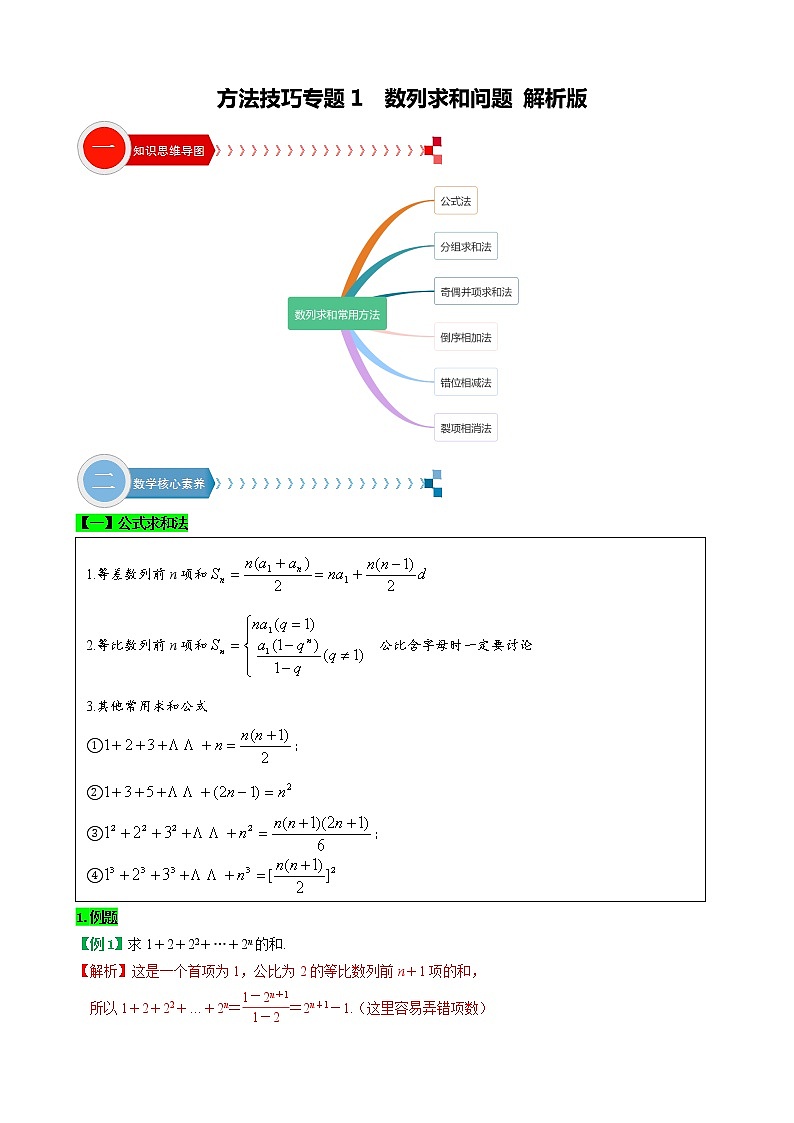
【一】公式求和法
1.等差数列前n项和
2.等比数列前n项和 公比含字母时一定要讨论
3.其他常用求和公式
①；
②
③；
④

1.例题
【例1】求1＋2＋22＋…＋2n的和.
【解析】这是一个首项为1，公比为2的等比数列前n＋1项的和，
所以1＋2＋22＋…＋2n＝＝2n＋1－1.（这里容易弄错项数）
【例2】已知等比数列{an}中，a3＝4，S3＝12，求数列{an}的通项公式.
【解析】当q＝1时，a3＝4，a1＝a2＝a3＝4，S3＝a1＋a2＋a3＝12，
所以q＝1符合题意，an＝4.
当q≠1时，解得q＝－，an＝a3qn－3＝n－5.
故数列通项公式为an＝4或an＝n－5.
【注意：上述解法中忽视了等比数列前n项和公式中q＝1这一特殊情况.】
【例3】在公差为的等差数列{}中，已知＝10，且，2＋2，5成等比数列．
(1)求，；
(2)若0，
由已知得
化简得即
又∵a1>0，q>0，∴a1＝1，q＝2，
∴数列{an}的通项公式为an＝2n－1.
(2)由(1)知bn＝a＋log2an ＝4n－1＋n－1，
∴Tn＝(1＋4＋42＋…＋4n－1)＋(0＋1＋2＋3＋…＋n－1)
＝＋＝＋.
【练习2】已知数列是等差数列，满足，，数列是公比为等比数列，且．
（1）求数列和的通项公式；
（2）求数列的前项和．
【解析】（1）∵数列是等差数列,满足，，
∴公差.∴数列的通项公式为.
因为，，∴，
又因为数列是公比为等比数列，∴. ∴.
（2）.
【三】奇偶并项求和法
奇偶并项求和的基本思路：有些数列单独看求和困难，但相邻项结合后会变成熟悉的等差数列、等比数列求和.但当求前n项和而n是奇数还是偶数不确定时，往往需要讨论.

1.例题
【例1】求和12－22＋32－42＋…＋992－1002.
【解析】12－22＋32－42＋…＋992－1002＝(12－22)＋(32－42)＋…＋(992－1002)
＝(1－2)(1＋2)＋(3－4)(3＋4)＋…＋(99－100)(99＋100)＝－(1＋2＋3＋4＋…＋99＋100)＝－5 050.
【例2】已知正项等比数列{an}的前n项和为Sn，且S2＝6，S4＝30，n∈N*，数列{bn}满足
bn·bn＋1＝an，b1＝1.
(1)求an，bn；
(2)求数列{bn}的前n项和Tn.
【解析】(1)设正项等比数列{an}的公比为q(q>0)，由题意可得a1＋a1q＝6，a1＋a1q＋a1q2＋a1q3＝30，解得a1＝q＝2(负值舍去)，可得an＝a1qn－1＝2n，由bn·bn＋1＝an＝2n，b1＝1，可得b2＝2，即有bn＋1·bn＋2＝an＋1＝2n＋1，可得＝2，可得数列{bn}中奇数项、偶数项分别为公比为2的等比数列，
即有
(2)当n为偶数时，前n项和为Tn＝(1＋2＋…＋)＋(2＋4＋…＋)
＝＝3·()n－3；
当n为奇数时，前n项和为Tn＝Tn－1＋＝3·()n-1－3＋＝()n+3－3.
综上可得，Tn＝
2.巩固提升综合练习
【练习1】已知为数列的前项和，且满足，，则_____．
【解析】由知，当时，．
所以，所以数列所有的奇数项构成以3为公比的等比数列，
所有的偶数项也构成以3为公比的等比数列．
又因为，所以，，．
所以．
【练习2】已知函数，且，则__________．
【答案】
【解析】当为奇数时，
.
当为偶数时，
.

所以


【四】倒序相加法求和
这是推导等差数列的前n项和公式时所用的方法，就是将一个数列倒过来排列（反序），再把它与原数列相加，就可以得到n个.

1.例题
【例1】求和
【解析】设 ①

②
①+②得，所以
【例2】设， .
【解析】由于，
故原式.
2.巩固提升综合练习
【练习1】已知正数数列是公比不等于1的等比数列，且，若，则（ ）
A．2018 B．4036 C．2019 D．4038
【解析】∵正数数列是公比不等于1的等比数列，且
∴，即.
∵函数，∴
令，则
∴
∴， 故选C.
【练习2】已知函数，若 ，则的最小值为（ ）
A． B． C． D．
【解析】由题知
令
又
于是有
因此
所以
当且仅当时取等号。本题正确选项：

【五】错位相减求和
数列{an·　bn}的前n项和，其中{ an }、{ bn }分别是等差数列和等比数列. 求和时一般在已知和式的两边都乘以组成这个数列的等比数列的公比；然后再将得到的新和式和原和式相减，转化为同倍数的等比数列求和，这种方法就是错位相减法。

1.例题
【例1】求和：1×21＋2×22＋3×23＋…＋n×2n，n∈N*.
【解析】设Sn＝1×21＋2×22＋3×23＋…＋n×2n，
则2Sn＝1×22＋2×23＋…＋(n－1)×2n＋n×2n＋1，
∴－Sn＝21＋22＋23＋…＋2n－n×2n＋1＝－n×2n＋1＝2n＋1－2－n×2n＋1＝(1－n)×2n＋1－2，
∴Sn＝(n－1)·2n＋1＋2.
【例2】在数列，中，，，.等差数列的前两项依次为，.
（1）求的通项公式；
（2）求数列的前项和.
【解析】
（1）∵，∴，，则的公差为
故的通项公式为.
（2），①
，②
①②得.
又，从而是首项为2，公比为2的等比数列，
故.
，
，
，
即，即.

2.巩固提升综合练习
【练习1】求和：
【解析】当时，
当时，
当且时， ①
②
①－②得

所以

【练习2】已知数列{an}满足an≠0，a1＝，an－an＋1＝2anan＋1，n∈N+.
(1)求证：是等差数列，并求出数列{an}的通项公式；
(2)若数列{bn}满足bn＝，求数列{bn}的前n项和Tn.
【解】　(1)由已知可得，－＝2，
∴是首项为3，公差为2的等差数列，
∴＝3＋2(n－1)＝2n＋1，∴an＝.
(2)由(1)知bn＝(2n＋1)2n，
∴Tn＝3×2＋5×22＋7×23＋…＋(2n－1)2n－1＋(2n＋1)2n……①
2Tn＝3×22＋5×23＋7×24＋…＋(2n－1)2n＋(2n＋1)·2n＋1……②
①－②得，－Tn＝6＋2×22＋2×23＋…＋2×2n－(2n＋1)2n＋1＝6＋－(2n＋1)2n＋1
＝－2－(2n－1)2n＋1，
∴Tn＝2＋(2n－1)2n＋1.
【练习3】已知等比数列的前项和为，若，则数列的前项和为（ ）
A． B． C． D．
【解析】
当 时，不成立，当 时， ，两式相除得 ，解得： ， 即 ， ， ，
，
两式相减得到： ，
所以 ，故选D.
【练习4】已知数列是公差不为0的等差数列，且成等比数列.
(1)求的通项公式;
(2)若,求的前项和.
【解析】（1）数列是公差不为0的等差数列，，且，，成等比数列，
，解得，或（舍，．
（2），
，①
，②
①②，得
，．

【六】裂项求和
这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项（通项）分解，然后重新组合，使之能消去一些项，最终达到求和的目的. 通项分解（裂项）如：
（1） [一般]
（2）
（3）
（4）
（5）

（6）
（7）
（8）


1.例题
【例1】已知等差数列为递增数列，且满足,．
（1）求数列的通项公式；
（2）令，为数列的前n项和，求．
【解析】（1）由题意知
，或
为递增数列，，故数列的通项公式为
（2）
.

【例2】求和：＋＋＋…＋，n≥2，n∈N*.
【解析】　∵＝＝，
∴原式＝＝
＝－(n≥2，n∈N*).
【例3】已知数列的前项和满足，且.
（1）证明数列为等差数列，并求的通项公式；
（2）设，为数列的前项和，求使成立的最小正整数的值.
【解析】（1） 当时，，[来源:学科网]
又，所以，
当时，，
所以，
可得，所以为等差数列.
又，得，又，所以.
（2）
，
所以.
要使，即，
解得，所以.
【例4】已知数列的通项公式为，求它的前n项和。
解：设则
所以，，解得，
所以


2.巩固提升综合练习
【练习1】设数列是公差不为零的等差数列，其前项和为，.若，，成等比数列.
（I）求及；
（Ⅱ）设， 求数列的前项和.
【解析】（Ⅰ）由题意，得，即，，解得，
所以，；
（Ⅱ）因为，
所以.
【练习2】在数列{an}中，已知a1＝1＋，且，n∈N*.
(1)记bn＝(an－1)2，n∈N*，证明数列{bn}是等差数列；
(2)设{bn}的前n项和为Sn，证明.
【解析】证明：(1)，
因为bn＋1－bn＝＝2，所以数列{bn}是以3为首项，2为公差的等差数列．
(2)由(1)得Sn＝＝n(n＋2)，所以
所以
.
【练习3】已知数列的首项，前项和为，且
（Ⅰ）设，证明数列是等比数列；
（Ⅱ）设，求的前项和的取值范围.
【解析】（Ⅰ）由知：当时
两式相减得：[来源:学.科.网]

又 ，
故
是公比为，首项为的等比数列
（Ⅱ）由（Ⅰ）知：
由 得：



是单调递增的，故 的取值范围是
【练习4】已知数列的前项和，等比数列的公比，且，是，的等差中项.
（1）求数列和的通项公式；
（2）求数列的前项和.
【解析】（1）解：∵，∴时，.又时，满足上式，
∴，∵，，∴，，[来源:学科网ZXXK]
又∵，，解得，，∴，.
（2）∵，
∴

【七】其他方法
1.例题
【例1】已知数列满足对时，，其对，有，则数列的前50项的和为__________．
【答案】
【解析】数列{an}满足对1≤n≤3时，an=n，且对∀n∈N*，有an+3+an+1=an+2+an，
可得a1=1，a2=2，a3=3，a4=1+3﹣2=2，
a5=2+2﹣3=1，a6=2，a7=3，a8=2，a9=1，a10=2，…，则数列{an}为周期为4的数列，且以1，2，3，2反复出现，可得数列{n•an}的前50项的和为
（1+5+…+49）+2（2+6+…+50）+3（3+7+…+47）+2（4+8+…+48）
=×（1+49）×13+2××（2+50）×13+3×（3+47）×12+2×（4+48）×12=2525．
故答案为：2525．
【例2】数列的首项为1，其余各项为1或2，且在第个1和第个1之间有个2，即数列为：1，2，1，2，2，2，1，2，2，2，2，2，1，…，记数列的前项和为，则__________．（用数字作答）
【答案】3993
【解析】第个1为数列第项，
当时；当时；
所以前2019项有45个1和个2，
因此
【例3】若数列满足， ，数列的通项公式 ，则数列的前10项和___________
【答案】
【解析】由，当n=1，代入得-4,依次得发现规律， 利用，得b=- ， ，求出.
故答案为：
【例4】等差数列中，，.若记表示不超过的最大整数，（如）.令，则数列的前2000项和为__________．
【答案】5445.
【解析】设等差数列{an}的公差为d，∵a3+a4=12，S7=49．
∴2a1+5d=12，d=49，解得a1=1，d=2．
∴an=1+2（n﹣1）=2n﹣1．bn=[lgan]=[lg（2n﹣1）]，
n=1，2，3，4，5时，bn=0．
6≤n≤50时，bn=1；
51≤n≤500时，bn=2；
501≤n≤2000时，bn=3．
∴数列{bn}的前2000项和=45+450×2+1500×3=5445．
故答案为：5445.
【例5】“斐波那契”数列由十三世纪意大利数学家斐波那契发现．数列中的一系列数字常被人们称之为神奇数．具体数列为1，1，2，3，5，8，即从该数列的第三项数字开始，每个数字等于前两个相邻数字之和．已知数列为“斐波那契”数列，为数列的前项和，若则__________．(用M表示)
【答案】
【解析】由“斐波那契”数列可知
。
所以 ，[来源:学科网ZXXK]
所以



三、课后自我检测
1．已知是上的奇函数，，则数列的通项公式为 ( )
A． B． C． D．
【解析】
[由在上为奇函数，知，令，则，得到．由此能够求出数列{的通项公式]
由题已知是上的奇函数
故，
代入得：
∴函数关于点对称，，令，则，得到．
∵，

倒序相加可得，即 ，故选：B．
2．设f(x)是R上的奇函数，当x＞0时，f(x)＝2x＋ln，记an＝f(n－5)，则数列{an}的前8项和为________．
【答案】－16
【解析】数列{an}的前8项和为
f(－4)＋f(－3)＋…＋f(3)＝f(－4)＋(f(－3)＋f(3))＋(f(－2)＋f(2))＋(f(－1)＋f(1))＋f(0)＝f(－4)＝－f(4)＝－＝－16.
3．.求和：Sn＝－1＋3－5＋7－…＋(－1)n(2n－1).
【解析】当n为奇数时，
Sn＝(－1＋3)＋(－5＋7)＋(－9＋11)＋…＋[(－2n＋5)＋(2n－3)]＋(－2n＋1)
＝2·＋(－2n＋1)＝－n.
当n为偶数时，
Sn＝(－1＋3)＋(－5＋7)＋…＋[(－2n＋3)＋(2n－1)]＝2·＝n.
∴Sn＝(－1)nn (n∈N*).
4．已知等差数列和等比数列满足a1=b1=1,a2+a4=10,b2b4=a5．
（1）求的通项公式；
（2）求和：．
【解析】（1）设等差数列{an}的公差为d.
因为a2+a4=10，所以2a1+4d=10.解得d=2.所以an=2n−1.
（2）设等比数列的公比为q.
因为b2b4=a5，所以b1qb1q3=9.解得q2=3.
所以.
从而.
5．等差数列的前项和为，已知，公差为大于0的整数，当且仅当=4时，取得最小值.
（1）求公差及数列的通项公式；
（2）求数列的前20项和.
（1）设的公差为，则由题可知：.
，即.
解得.
因为为整数，=2

所以数列的通项公式为
（2）当时，；当时，


=272 [来源:Z&xx&k.Com]
6．已知数列满足：，，.
（1）求、、；
（2）求证：数列为等比数列，并求其通项公式；
（3）求和.
【解析】（1）， ，
可得；
，；
（2）证明：
，
可得数列为公比为，首项为等比数列，即；
（3）由（2）可得，
．
7．已知数列是首项为，公差为的等差数列.
（1）若，，，数列的前项积记为，且，求的值；
（2）若，且恒成立，求的通项公式.
【解析】（1）设的前项和为，则，
∴，令；
（2）当时，，∴或（舍）.
当时，，解得或.
若，当时，，解得或（舍去）.此时不成等差数列，故舍去.
当时，依题意可知：数列是等差数列，故，
∴；
8．已知数列有，是它的前项和，且．
（1）求证：数列为等差数列.
（2）求的前项和.
【解析】（1）当时，
所以，，
两式对应相减得，
所以
又n=2时，
所以，所以，
所以数列为等差数列.
（2）当为偶数时，


当为奇数时，


综上：
9．已知数列满足,.
（1）证明:数列为等比数列;
（2）求数列的前项和.
【解析】（1） ， ，
则，又，
是以为首项，为公比的等比数列.
（2）由（1）知，
，
故其前项和为:.
数列的前项和为:.
10．在正项等比数列{}中，且成等差数列.
（1）求数列的通项公式；
（2）若数列{}满足，求数列{}的前项和．
【解析】设正项等比数列{an}的公比为(,
（1）∵∴,所以
∴q＝2，(舍去)，所以；
（2）∵，
∴，①
，②
①﹣②得＝，
∴.
11．已知正项数列其前n项和满足，且是和的等比中项.
（1）求证：数列为等差数列，并计算数列的通项公式；
（2）符号[x]表示不超过实数x的最大整数，记 ，求.
【分析】
（1）由得，从而得到，由此利用是和的等比中项，能求出数列的通项公式（2）由，令，得到，由此利用错位相减法能求出.
【解析】
（1）∵正项数列，前n项和Sn满足，①
，②
由①-②，得，
整理，得，
∵是正数数列，，
∴是公差为4的等差数列，
由得或，
当 时，，不满足是和的等比中项，
当时，，满足是和的等比中项，
.
（2），
由符号[x]表示不超过实数x的最大整数，知当时，，
令，
，
，③
，④
③-④，得，
，
.
12．已知公差不为0的等差数列的前n项和为，，且，，成等比数列．
（1）求数列的通项公式；
（2）求数列的前n项和公式．
【解析】（1）公差d不为0的等差数列的前n项和为，
，可得，
且，，成等比数列，可得，即，
解得，，
则；
，
，
则数列的前n项和为
．
13．已知正项数列{an}的前n项和为Sn，a1＝1，且(t＋1)Sn＝a＋3an＋2(t∈R)．
(1)求数列{an}的通项公式；
(2)若数列{bn}满足b1＝1，bn＋1－bn＝an＋1，求数列的前n项和Tn.
【解析】　(1)因为a1＝1，且(t＋1)Sn＝a＋3an＋2，
所以(t＋1)S1＝a＋3a1＋2，所以t＝5.
所以6Sn＝a＋3an＋2. (ⅰ)
当n≥2时，有6Sn－1＝a＋3an－1＋2，(ⅱ)
①－②得6an＝a＋3an－a－3an－1，所以(an＋an－1)(an－an－1－3)＝0，
因为an>0，所以an－an－1＝3，
又因为a1＝1，所以{an}是首项a1＝1，公差d＝3的等差数列，
所以an＝3n－2(n∈N+)．
(2)因为bn＋1－bn＝an＋1，b1＝1，所以bn－bn－1＝an(n≥2，n∈N+)，
所以当n≥2时，bn＝(bn－bn－1)＋(bn－1－bn－2)＋…＋(b2－b1)＋b1＝an＋an－1＋…＋a2＋b1＝.
又b1＝1也适合上式，所以bn＝(n∈N+)．
所以＝＝·＝·，
所以Tn＝·＝·＝.
14．已知数列与的前项和分别为和，且对任意恒成立．
（1）若，求；
（2）若对任意，都有及成立，求正实数的取值范围．
【分析】（1）根据可得．再由，利用等差数列的通项公式求和公式即可得出．
（2）对任意，，
∴．．即，．
∴数列是等比数列，公比为2．∴．
又．利用成立，及其数列的单调性即可得出．
【解析】（1），∴时，．
时，．时适合上式．
．
，，又．
数列是等差数列，首项为2，公差为1．
．
（2）对任意，都有，．
．，．
数列是等比数列，公比为2．
．
又．
成立，
，

对任意，都成立，∴，正实数的取值范围是．
15．已知数列的首项，其前和为，且满足.
（1）用表示的值；
（2）求数列的通项公式；
（3）当时，证明：对任意，都有.
【分析】
（1）令即可求解；
（2）当时，通过作差法可求得，再书写一项，通过两式作差可得，分类讨论的奇偶，即可求解；
（3）可结合放缩法公式，，分别对化简后的表达式
进行放缩，
再结合裂项公式，的特点即可进一步求解
【解析】（1）由条件得，.
（2）法一：由条件得，
两式相减得，故，
两式再相减得，
构成以为首项，公差为的等差数列；
构成以为首项，公差为的等差数列；
由（1）得；
由条件得，得，从而，

法二：
设，即
则有
时，，即

（3）证明：当时，且，由（2）可知
①当时，
②当时，，






.