方法技巧专题05 立体几何中平行与垂直证明-2022年高考数学满分之路方法技巧篇

这是一份方法技巧专题05 立体几何中平行与垂直证明-2022年高考数学满分之路方法技巧篇，文件包含方法技巧专题05立体几何中平行与垂直证明解析版doc、方法技巧专题05立体几何中平行与垂直证明原卷版doc等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
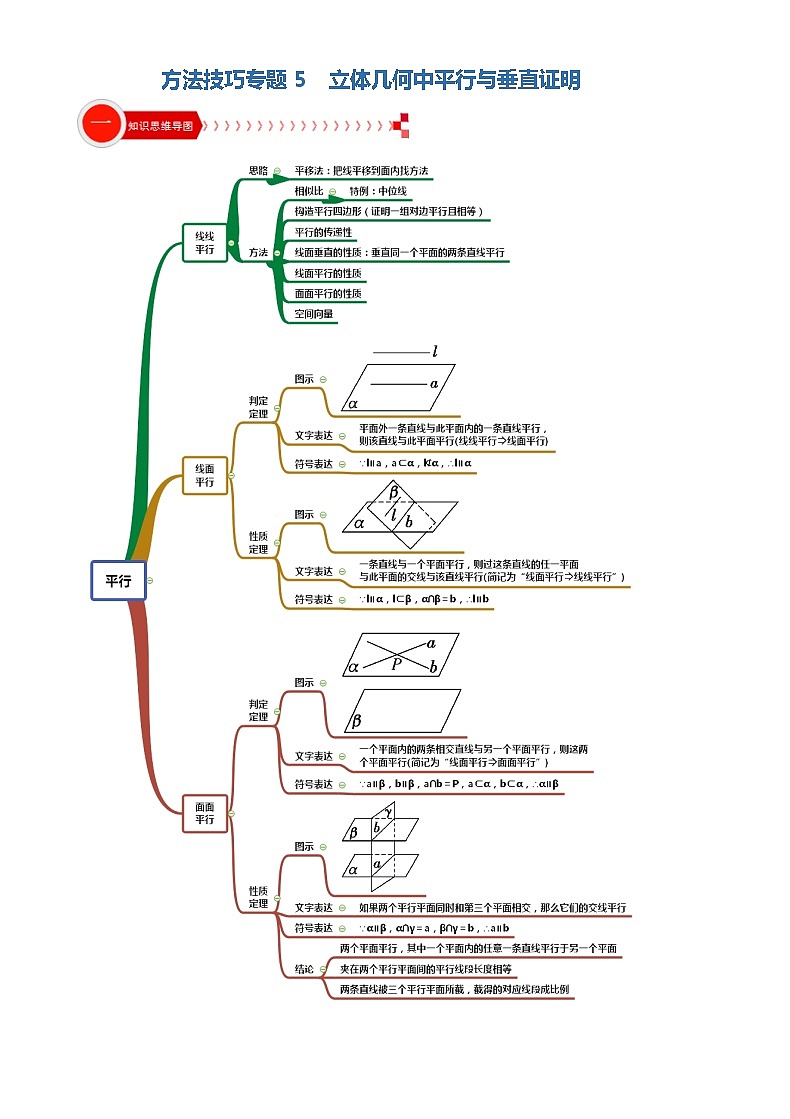
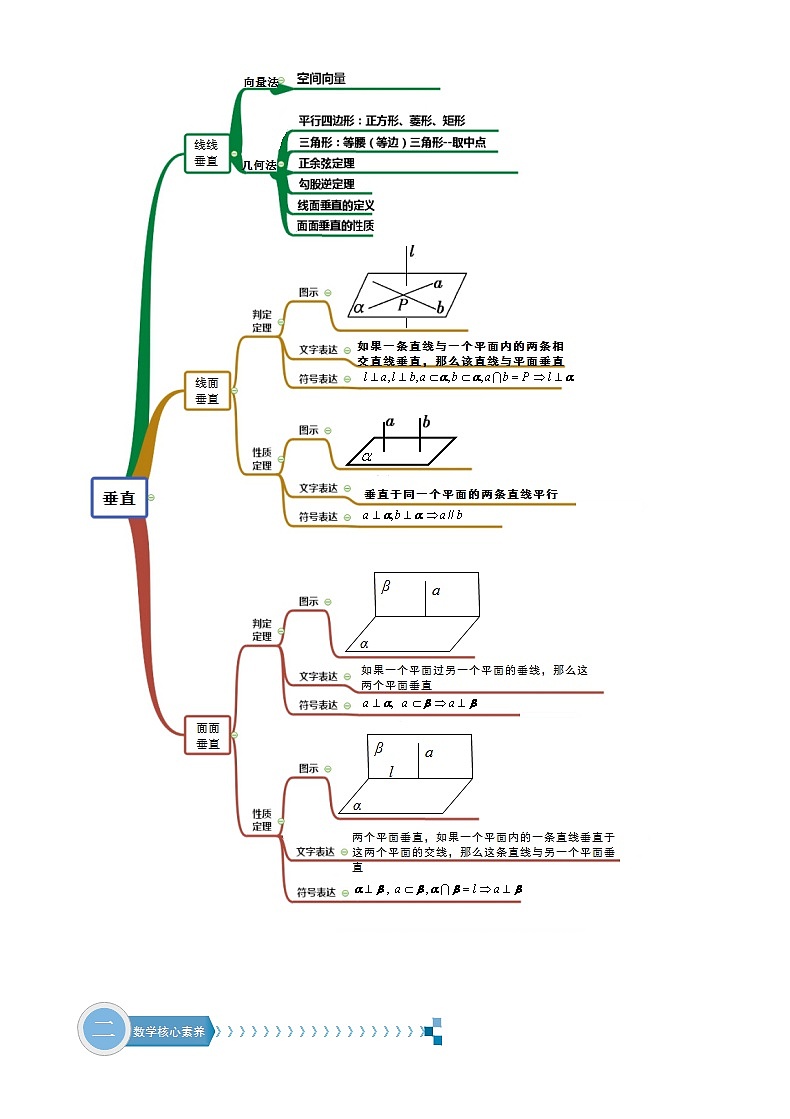
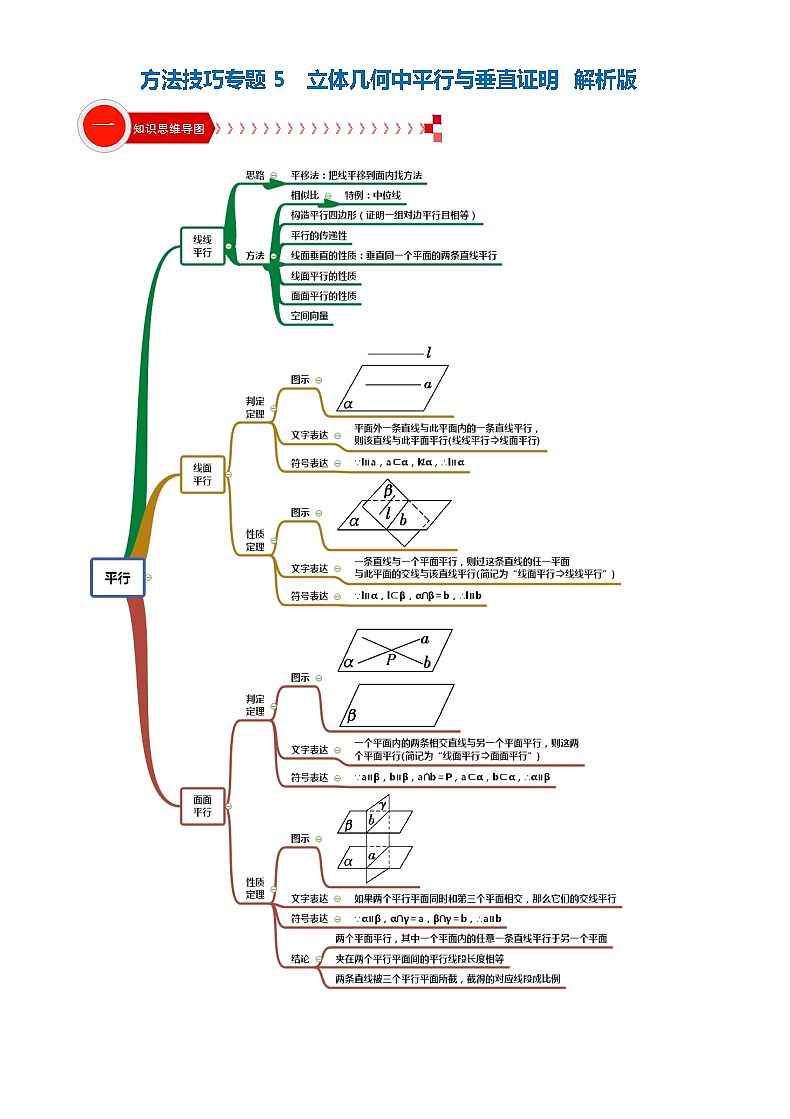
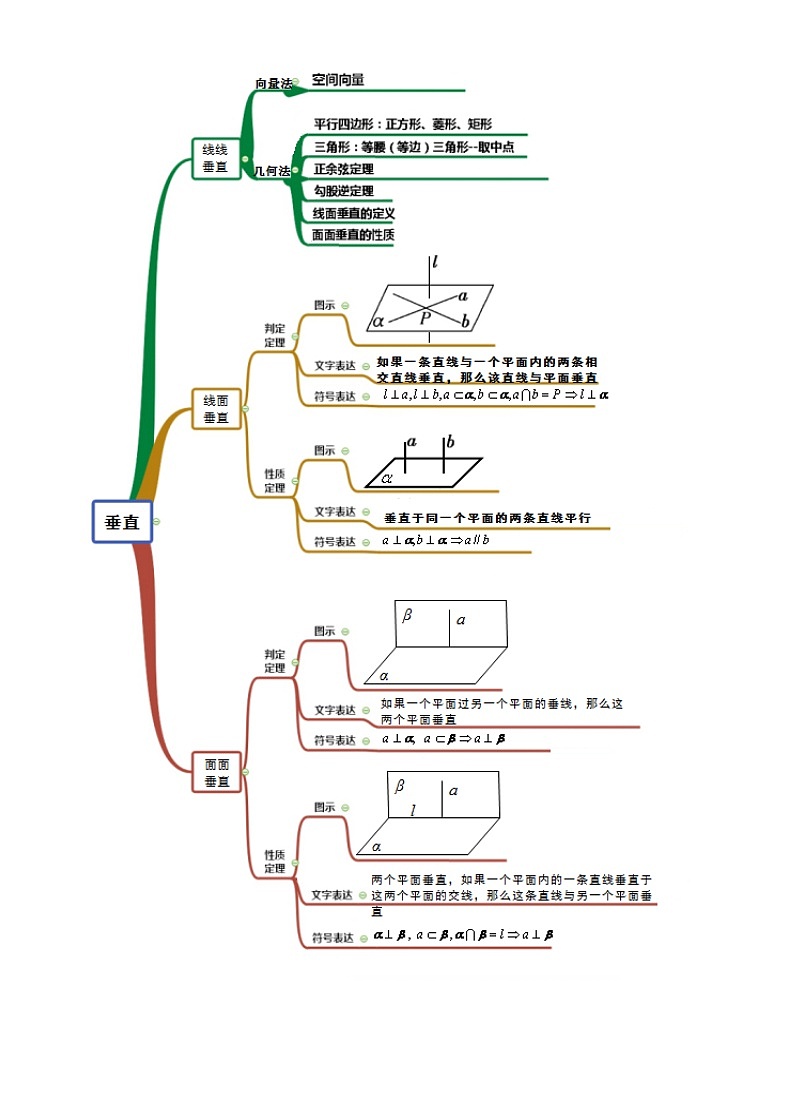
方法技巧专题5  立体几何中平行与垂直证明 解析版  【一】“平行关系”常见证明方法1.1 直线与直线平行的证明1.1.1 利用某些平面图形的特性：如平行四边形的对边互相平行等1.1.2 利用三角形中位线性质1.1.3 利用空间平行线的传递性（即公理4）：平行于同一条直线的两条直线互相平行。 1.1.4 利用直线与平面平行的性质定理：如果一条直线与一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。     1.1.5 利用平面与平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．     1.1.6 利用直线与平面垂直的性质定理：垂直于同一个平面的两条直线互相平行。1.1.7 利用平面内直线与直线垂直的性质：在同一个平面内，垂直于同一条直线的两条直线互相平行。1.1.8 利用定义：在同一个平面内且两条直线没有公共点1.2 直线与平面平行的证明1.2.1 利用直线与平面平行的判定定理：平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行。   1.2.2 利用平面与平面平行的性质推论：两个平面互相平行，则其中一个平面内的任一直线平行于另一个平面。1.2.3 利用定义：直线在平面外，且直线与平面没有公共点1.3 平面与平面平行的证明1.3.1 利用平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。1.3.2 利用某些空间几何体的特性：如正方体的上下底面互相平行等1.3.3 利用定义：两个平面没有公共点 1.例题【例1】 如图，已知菱形，其边长为2，，绕着顺时针旋转得到，是的中点．（1）求证：平面；（2）求直线与平面所成角的正弦值．证明（1）连结AC交BD于点O，连结OM在菱形中，O为AC中点，M为的中点OM为APC的中位线，OM∥AP    ---------------（利用1.1.2中位线性质）又OM面，且PA面平面  ----------------（利用1.2.1直线与平面平行的判定定理） 【例2】 已知四棱锥P-ABCD，底面ABCD是、边长为的菱形，又，且PD=CD，点M、N分别是棱AD、PC的中点． 证明：DN//平面PMB。   证明：取PB中点为E，连结ME、NE点M、N分别是棱AD、PC的中点 NE  BC ,又MD  BC NE   MD，即四边形ABCD为平行四边形．　ME//DN   ----------（利用1.1.1平行四边形性质）又 ME面PMB，且DN面PMB， DN//平面PMB----------（利用1.2.1直线与平面平行的判定定理）【例3】如图，已知点是平行四边形所在平面外的一点，，分别是，上的点且，求证：平面．         证明：过E作EM//AD交PD于点M ,连结MF=     ==  PB//MF，又AD//BC，EM//BCBC面PBC，且EM面PBC，EM//面PBC，同理MF//面PBC，----------（利用1.2.1直线与平面平行的判定定理）FM面EFM，EM面EFM，EM MF于点M,   面EMF//面PBC,       ------------（利用1.3.1 平面与平面平行的判定定理)EF//面PBC          ------------ (利用1.2.2平面与平面平行的性质)2.巩固提升综合练习【练习1】如图，在六面体中，平面∥平面，⊥平面，,,∥,且,．   求证： ∥平面；     证明：取DG的中点为M连结FM、AM，∴DM=MG=EF=1又∵∥∴四边形EFMD为平行四边形，∴EF    DE∵⊥平面,且平面∥平面∴AD⊥DE,AD⊥AB,又∵AB、DE面ABED, AB=DE=2 ∴AB   DE∴AB    FM,即四边形ABFM为平行四边形，∴BF∥AM，又∵BF 面，AM面∴∥平面 【练习2】如图，，，，分别是正方体的棱，，，的中点．求证：（1）平面；（2）平面平面．【解析】证明（1）如图，取的中点，连接，，[来源:学&科&网Z&X&X&K]因为，所以，所以四边形为平行四边形，故，因为平面，平面，所以平面．（2）由题意可知．连接，，因为，所以四边形是平行四边形，故又，，所以平面平面．【练习3】在如图所示的五面体中，四边形为菱形，且， 平面， ， 为中点.求证： 平面. 【解析】证明：取中点，连接，因为分别为中点，所以，又平面，且平面，所以平面，因为平面， 平面，平面平面，所以．又， ，所以， .所以四边形为平行四边形.所以.又平面且平面，所以平面，又，所以平面平面.又平面，所以平面. 【二】“垂直关系”常见证明方法[来源:Zxxk.Com]2.1直线与直线垂直的证明2.1.1 利用某些平面图形的特性：如直角三角形的两条直角边互相垂直,等边、等腰三角形（中线即高线），正方形、矩形邻边垂直，正方形菱形对角线垂直等。2.1.2 看夹角：两条共（异）面直线的夹角为90°，则两直线互相垂直。2.1.3 利用直线与平面垂直的性质：如果一条直线与一个平面垂直，则这条直线垂直于此平面内的所有直线。     2.1.4 利用平面与平面垂直的性质推论：如果两个平面互相垂直，在这两个平面内分别作垂直于交线的直线，则这两条直线互相垂直。2.1.5 利用常用结论：①     如果两条直线互相平行，且其中一条直线垂直于第三条直线，则另一条直线也垂直于第三条直线。    ②     如果有一条直线垂直于一个平面，另一条直线平行于此平面，那么这两条直线互相垂直。 2.2 直线与平面垂直的证明2.2.1 利用某些空间几何体的特性：如长方体侧棱垂直于底面 等2.2.2 看直线与平面所成的角：如果直线与平面所成的角是直角，则这条直线垂直于此平面。2.2.3 利用直线与平面垂直的判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线垂直于此平面。           2.2.4 利用平面与平面垂直的性质定理：   两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。2.2.5 利用常用结论：①       一条直线平行于一个平面的一条垂线，则该直线也垂直于此平面。②       两个平面平行，一直线垂直于其中一个平面，则该直线也垂直于另一个平面。 2.3 平面与平面垂直的证明2.3.1 利用某些空间几何体的特性：如长方体侧面垂直于底面等2.3.2 看二面角：两个平面相交，如果它们所成的二面角是直二面角（即平面角是直角的二面角），就说这连个平面互相垂直。2.3.3 利用平面与平面垂直的判定定理一个平面过另一个平面的垂线，则这两个平面垂直。    1.例题【例1】如图,四边形ABCD为矩形，CF⊥平面ABCD，DE⊥平面ABCD，AB=4a，BC= CF=2a，P为AB的中点.求证：平面PCF⊥平面PDE.    证明：ABCD为矩形，AB=2BC, P为AB的中点，PBC为等腰直角三角形，∠BPC=45°.同理可证∠APD=45°. ∠DPC=90°，即PC⊥PD.   ----------- （利用2.1.1）又DE⊥面ABCD，PC面ABCD，PC⊥DE.     ----------- （利用2.1.3）DE∩PD=D ，PC ⊥面PDE .     ----------- （利用2.2.3）又PC面PCF，面PCF⊥面PDE。----------- （利用2.3.3） 【例2】如图，在四棱锥中，ABCD是矩形，，，点是的中点，点在上移动。求证：。【证明】，  ----------- （利用2.1.3） ，----------- （利用2.1.1） ，----------- （利用2.2.3）     ，点是的中点  ----------- （利用2.1.1）     又           ----------- （利用2.1.3）  【例3】如图，在四边形中，，，点为线段上的一点.现将沿线段翻折到，使得平面平面，连接，.证明：平面.【证明】(Ⅰ)连结，交于点,在四边形中，∵，∴，∴,∴又∵平面平面，且平面平面=∴平面----------- （利用2.2.4）  2.巩固提升综合练习【练习1】 如图，四棱锥S-ABCD的底面是矩形，SA底面ABCD，P为BC边的中点，SB与平面ABCD所成的角为，且AD=2，SA=1。求证：PD平面SAP；【证明】∵SA⊥面ABCD，∴SBA为SB与面ABCD的夹角，∴SBA =，且SA⊥AB，∴AB=1在矩形ABCD中，P为BC边的中点，∴AB=BP=1, ∴AP=, 同理DP=又∵AD=2，∴APD=,即AP⊥PD∵SA⊥面ABCD, ∴SA⊥PD,  且SA、AP面SAP，SAAP于点A,∴PD平面SAP 【练习2】 如图，在三棱柱中，侧棱底面，为棱的中点．，，．（1）求证：平面；（2）求证：平面；【解析】（1）证明：连接与，两线交于点，连接．在中，∵，分别为，的中点，∴，又∵平面，平面，∴平面．（2）证明：∵侧棱底面，平面，∴，又∵为棱的中点，，∴．∵，，平面，∴平面，∴∵，∴．又∵，∴在和中，，∴，即，∴∵，，平面，∴平面．【练习3】如图，四棱锥中，，，，为正三角形．且．证明：平面平面．【解析】（1）证明：∵，且，∴，又为正三角形，∴，又∵，，∴，又∵，，∴，，∴平面，又∵平面，∴平面平面．1．如图，四边形为正方形，平面，，，，．（1）求证：；（2）若点在线段上，且满足，求证：平面；（3）求证：平面． 【解析】（1）∵，∴与确定平面，∵平面，∴．由已知得且，∴平面．又平面，∴．（2）过作，垂足为，连接，则．又，∴．又且，∴且，∴四边形为平行四边形，∴．又平面，平面，∴平面．（3）由（1）可知，．在四边形中，，，，，∴，则．设，∵，故，则，即．又∵，∴平面．2．直三棱柱中， ， ， ，点是线段上的动点.（1）当点是的中点时，求证： 平面；（2）线段上是否存在点，使得平面平面？若存在，试求出的长度；若不存在，请说明理由.【解析】（1）如图，连接，交于点，连接，则点是的中点，又点是的中点，由中位线定理得，因为平面， 平面，所以平面.（2）当时平面平面.证明：因为平面， 平面，所以．又， ，所以平面，因为平面，所以平面平面，故点满足.因为， ， ，所以，故是以角为直角的三角形，又，所以.3.如图， 为等边三角形， 平面， ， ， 为的中点.（Ⅰ）求证： 平面；（Ⅱ）求证：平面平面.【解析】（1）证明：取的中点，连结∵在中， ， ∵， ∴， ∴四边形为平行四边形 ∴又∵平面 ∴平面（2）证：∵面， 平面，∴，又∵为等边三角形，∴，又∵，∴平面，又∵，∴面，又∵面，∴面面[来源:Z§xx§k.Com] 已知平面四边形中， 中， ，现沿进行翻折，得到三棱锥，点， 分别是线段， 上的点，且平面.求证：（1）直线平面；[来源:学*科*网]（2）当是中点时，求证：平面平面. 【解析】（1）证明：因为平面， 平面，平面平面，所以因为平面， 平面，所以 //平面（2）因为是的中点， ，所以为的中点.[来源:学科网]又因为，所以又， ，所以，， 平面， ，所以平面.因为平面，所以平面平面.