方法技巧专题10 圆锥曲线中的垂径定理-2022年高考数学满分之路方法技巧篇

这是一份方法技巧专题10 圆锥曲线中的垂径定理-2022年高考数学满分之路方法技巧篇，文件包含方法技巧专题10圆锥曲线中的垂径定理解析版docx、方法技巧专题10圆锥曲线中的垂径定理原卷版docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。
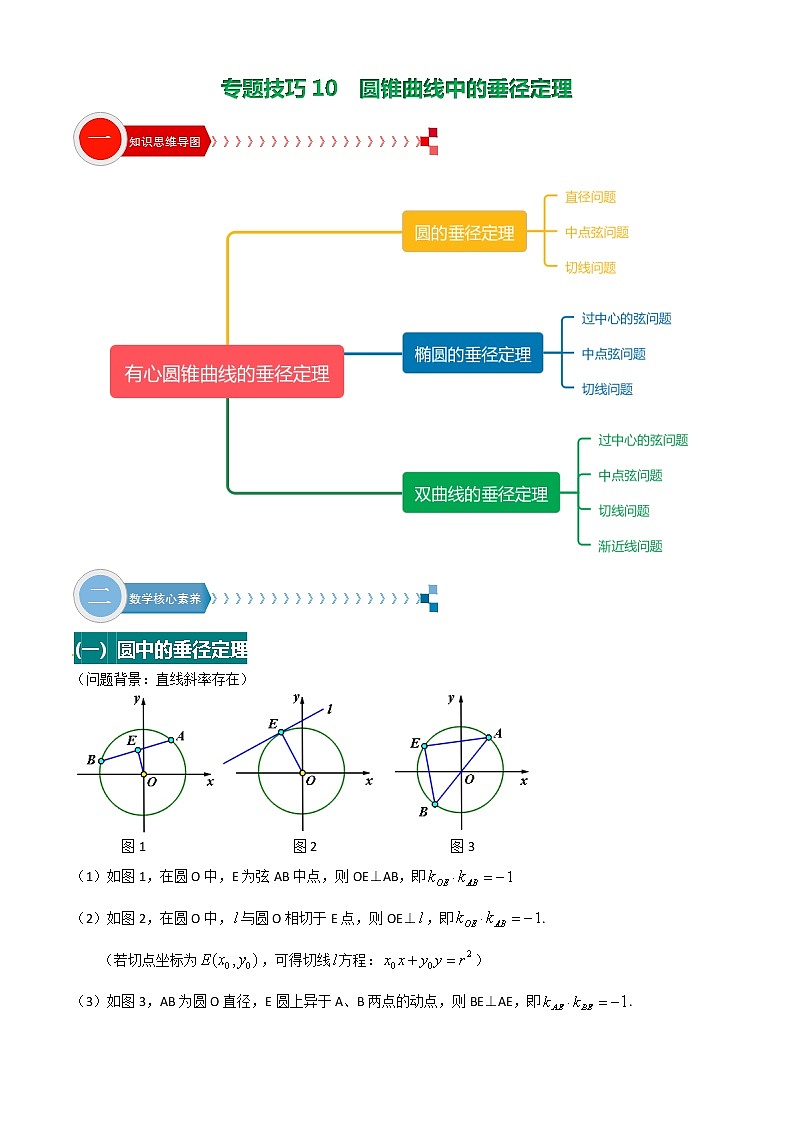
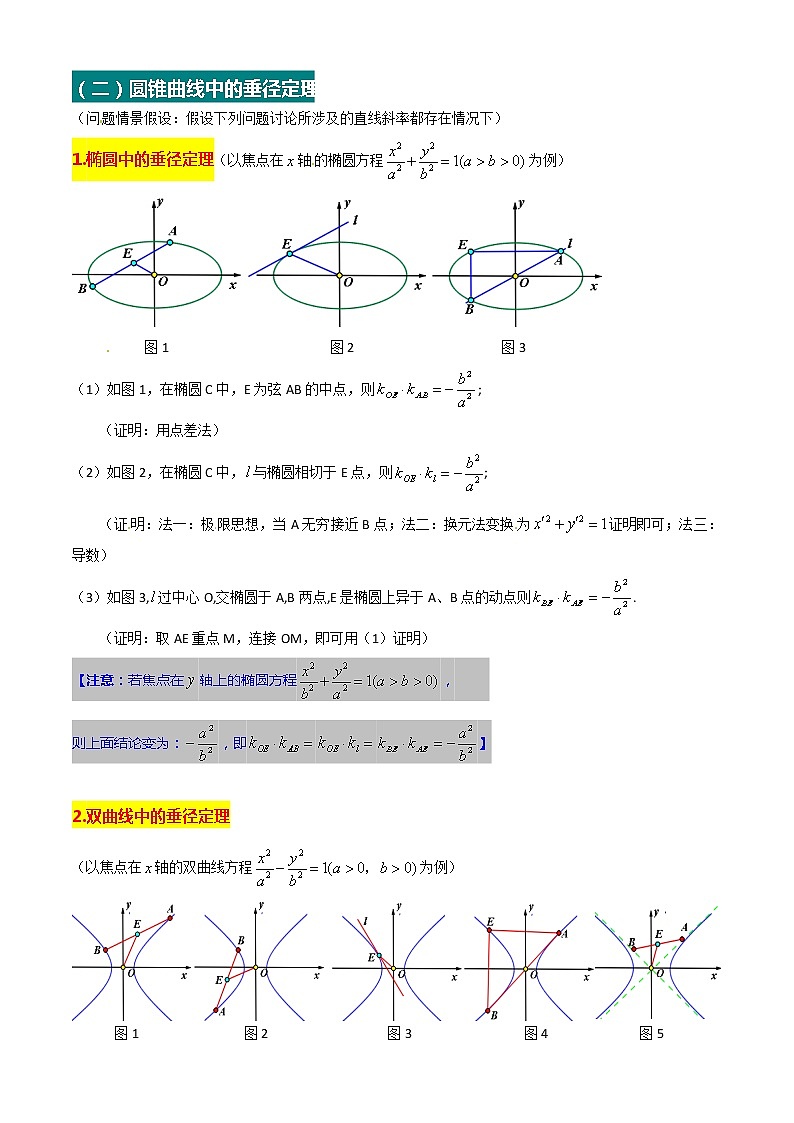
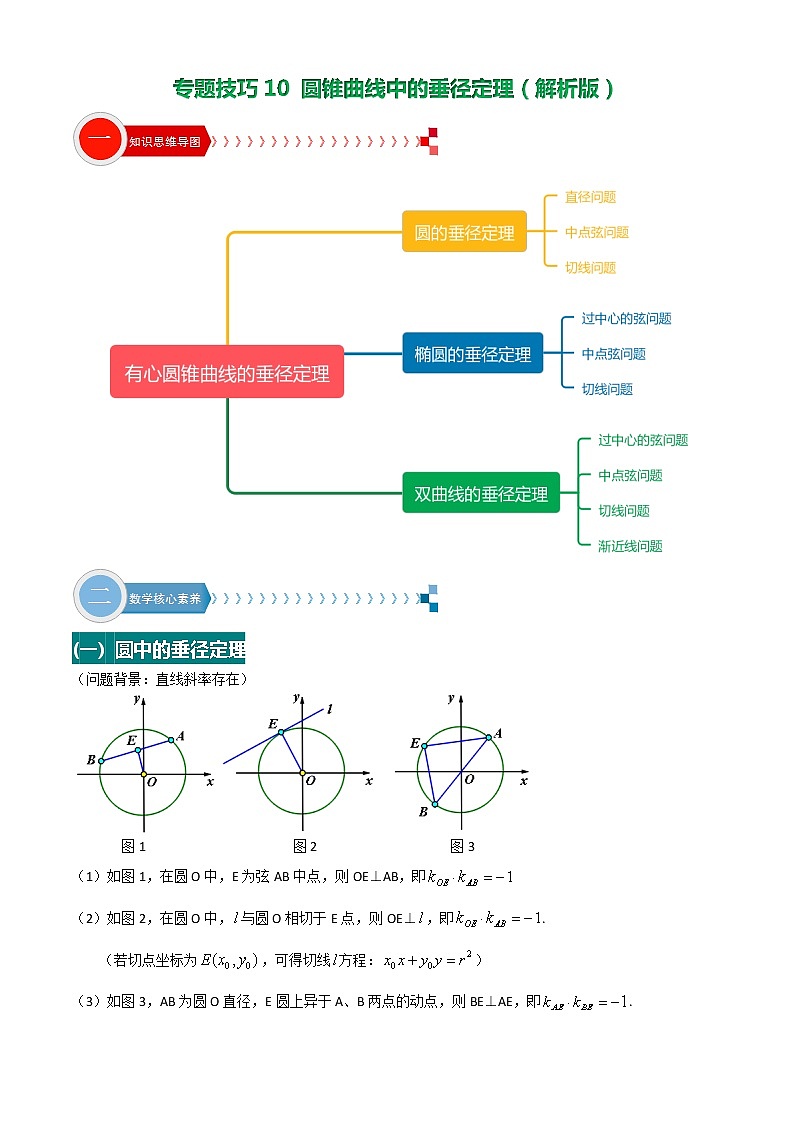
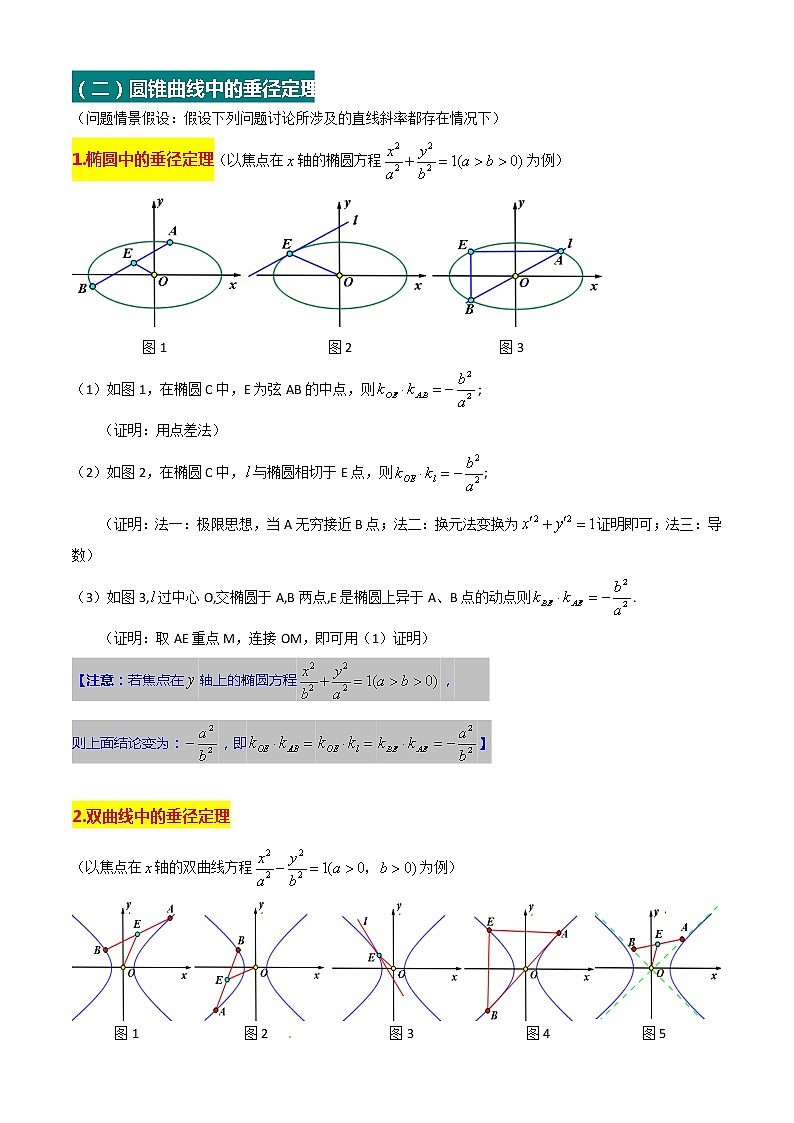
专题技巧10  圆锥曲线中的垂径定理(一) 圆中的垂径定理（问题背景：直线斜率存在）       图1                     图2                   图3（1）如图1，在圆O中，E为弦AB中点，则OE⊥AB，即（2）如图2，在圆O中，与圆O相切于E点，则OE⊥，即.（若切点坐标为，可得切线方程：）（3）如图3，AB为圆O直径，E圆上异于A、B两点的动点，则BE⊥AE，即.（二）圆锥曲线中的垂径定理（问题情景假设：假设下列问题讨论所涉及的直线斜率都存在情况下）1.椭圆中的垂径定理（以焦点在轴的椭圆方程为例）              图1                       图2                     图3（1）如图1，在椭圆C中，E为弦AB的中点，则;（证明：用点差法）[来源:Z+xx+k.Com]（2）如图2，在椭圆C中，与椭圆相切于E点，则;（证明：法一：极限思想，当A无穷接近B点；法二：换元法变换为证明即可；法三：导数）[来源:学+科+网Z+X+X+K]（3）如图3,过中心O,交椭圆于A,B两点,E是椭圆上异于A、B点的动点则.（证明：取AE重点M，连接OM，即可用（1）证明）【注意：若焦点在轴上的椭圆方程，     则上面结论变为：，即】 2.双曲线中的垂径定理（以焦点在轴的双曲线方程为例）      图1               图2                 图3                图4             图5（1）如图1或图2，E为弦AB的中点，则;（2）如图3，与双曲线相切于E点，则;（3）如图4，过O点的交双曲线于A,B两点，E是双曲线上异于A、B点的动点,则.（4）如图5，交上双曲线两渐近线于A,B两点，E为线段AB的中点，则.【注意：若焦点在轴上的双曲线方程，则上面斜率乘积结论变为：，即】（三）例题点评1.例题初探【例1】过点M(1,1)作斜率为的直线与椭圆相交于A,B两点，若M是线段AB的中点，则该椭圆的离心率为       .【例2】已知A、B为椭圆的左右顶点，P为椭圆上异于A、B的点，PA、PB的斜率分别为，且，则该椭圆的离心率为              【例3】设双曲线C：的顶点为，P为双曲线上一点，直线交双曲线C的一条渐近线于M点，直线和的斜率分别为，若且，则双曲线C离心率为（     ）A、2        B、        C、        D、4 【例4】已知A、B是双曲线的两个顶点，P是双曲线上异于A、B的另一点，P关于轴的对称点为，记直线AP、BQ的斜率分别为，且，则双曲线的离心率为               【例5】过双曲线的左焦点F且斜率为1的直线与双曲线的两条渐近线交于A、B两点，记线段AB的中点为M，且等于半焦距，则双曲线的离心率           【例6】已知直线的斜率为1，且与双曲线相切于第一象限于点，则点的坐标为______.     2.提高与巩固例题【例1】已知直线交椭圆于M、N两点，B是椭圆与轴正半轴的交点，若△BMN的重心恰好为椭圆的右焦点，则直线的方程为               【例2】已知椭圆，P是椭圆的上顶点，过P作斜率为的直线交椭圆于另一点A，设点A关于原点的对称点为B，（1）求△PAB面积的最大值（2）设线段PB的中垂线与轴交于点N，若点N在椭圆内部，求斜率的取值范围                 【例3】设直线与双曲线两条渐近线分别交于A，B，若点满足，则该双曲线的离心率是                 [来源:学.科.网] 【例4】已知某椭圆的焦点是，过点并垂直于x轴的直线与椭圆的一个交点为B，且．椭圆上不同的两点满足条件：成等差数列．(1) 求该椭圆的方程；(2) 求弦AC中点的横坐标；(3) 设弦AC的垂直平分线的方程为y=kx+m，求m的取值范围．       1.如图，已知椭圆，过原点的直线交椭圆于点P、A两点（其中点P在第一象限），过点P作轴的垂线，垂线为C，连AC并延长交椭圆于B，若，则椭圆的离心率为       2.已知双曲线的左右焦点为，右顶点为A，P为双曲线右支上一点，交双曲线的左支于点Q，与渐近线交于点R，线段PQ的中点为M，若，，则双曲线的离心率为          [来源:学_科_网] 3.如图，已知椭圆的左右顶点分别为A、B，P为第一象限内一点，且，连接PA交椭圆于点C，连BC、OP，若，则椭圆的离心率为         4.如图，，分别是双曲线C：的左右焦点，B是虚轴的端点，直线与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线MN与轴交于点M，若，则C的离心率是       。 5.过点作直线与椭圆交于两点，求的中点的轨迹的方程。     6.过点作直线与有心圆锥曲线交于两点，是否存在这样的直线使点为线段的中点？若存在，求直线的方程；若不存在，说明理由.         [来源:Zxxk.Com]7.如图，，椭圆C：，不过原点O的直线与C相交于A、B两点，且线段AB被直线OP平分，求△ABP的面积取最大值时直线的方程       8.已知椭圆的离心率为，直线与相切于点E. 求椭圆的方程.