方法技巧专题16 函数中恒成立与存在性问题-2022年高考数学满分之路方法技巧篇

这是一份方法技巧专题16 函数中恒成立与存在性问题-2022年高考数学满分之路方法技巧篇，文件包含方法技巧专题16函数中恒成立与存在性问题解析版docx、方法技巧专题16函数中恒成立与存在性问题原卷版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。
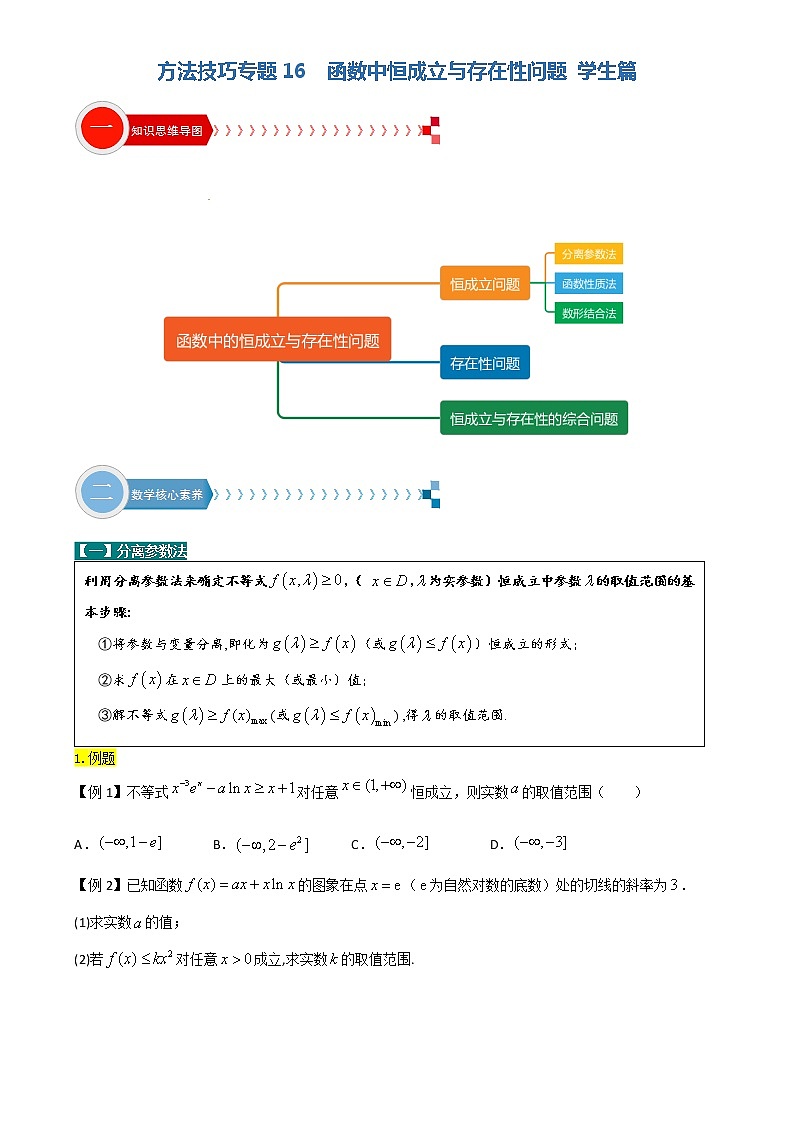
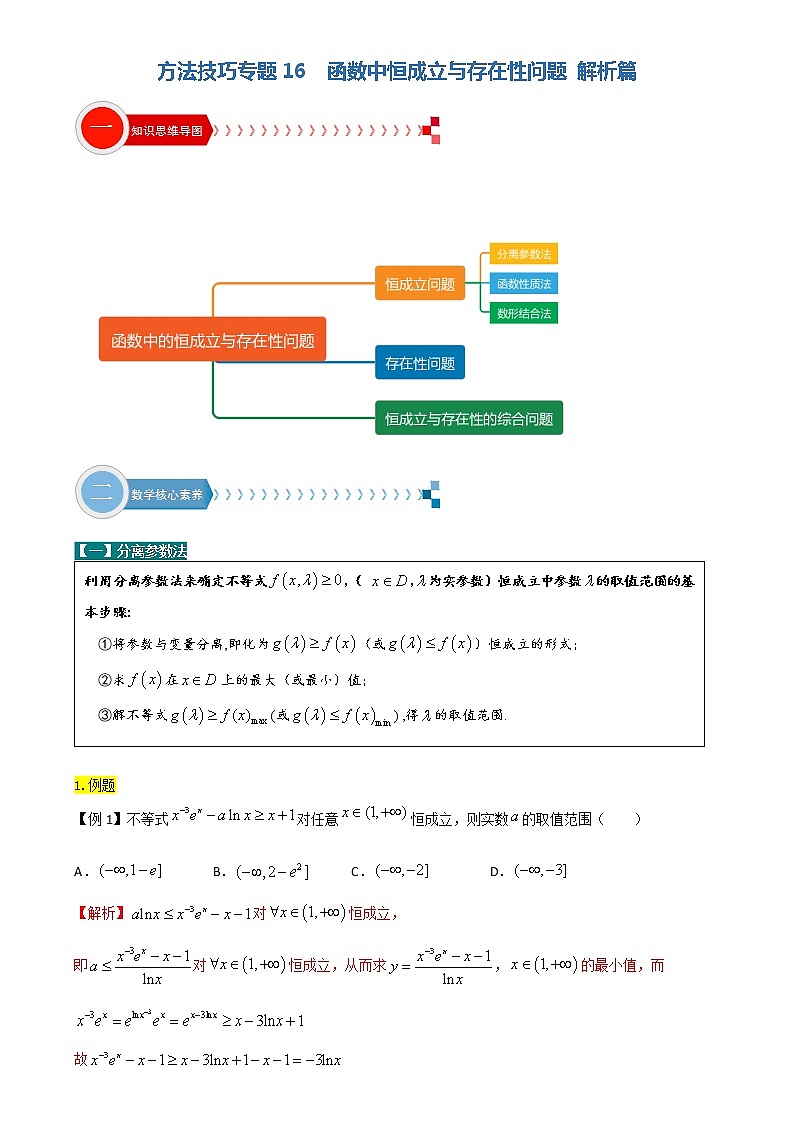
方法技巧专题16  函数中恒成立与存在性问题 学生篇          一、 函数中恒成立与存在性问题知识框架                                       二、函数中恒成 【一】分离参数法1.例题【例1】不等式对任意恒成立，则实数的取值范围（    ）A． B． C． D．【例2】已知函数的图象在点（为自然对数的底数）处的切线的斜率为．(1)求实数的值；(2)若对任意成立,求实数的取值范围.      2.巩固提升综合练习【练习1】已知函数,,其中且,．(1)若,且时,的最小值是－2,求实数的值；(2)若,且时,有恒成立,求实数的取值范围.        【练习2】若，恒成立，则的最大值为（   ）A． B． C． D．【练习3】已知，设函数若关于的不等式在上恒成立，则的取值范围为（    ）A． B． C． D． 【二】函数性质法1.例题【例1】定义域为的函数满足，当时，，若当时，不等式恒成立，则实数的取值范围是（   ）A．   B．   C．   D． 【例2】若对，，且，都有，则的取值范围是（    ）注:（ 为自然对数的底数，即…）A． B． C． D． 【例3】已知函数，对任意x∈[1，＋∞)，当恒成立时实数m的最大值为1，则实数a的取值范围是          ．    2.巩固提升综合练习【练习1】已知函数，，当时，不等式恒成立，则实数的取值范围为（   ）A．    B．    C．    D．【练习2】已知定义在上的偶函数在上递减，若不等式对恒成立，则实数的取值范围是（    ）A． B． C． D．【练习3】若，满足恒成立，则实数的取值范围为__________．  【三】数形结合法 1.例题【例1】已知函数,在恒有,求实数的取值范围.       【例2】已知函数f(x)＝若对于∀t∈R，f(t)≤kt恒成立，则实数k的取值范围是________．2.巩固提升综合练习【练习1】已知定义在上的奇函数满足:当时,,若不等式对任意实数恒成立,则实数的取值范围是（   ）A．                                     B．C.                              D．【练习2】若不等式对任意恒成立,实数x的取值范围是     . 【练习3】已知函数 若不等式对任意上恒成立，则实数的取值范围为（    ）                 三、函数中存在性问题                [来源:学§科§网]1.例题【例1】 已知函数f(x)＝x，若存在x∈，使得f(x)<2，则实数a的取值范围是________． 【例2】已知,,若存在,使得,求实数的取值范围；      【例3】已知,,若存在,使得,求实数的取值范围.      2.巩固提升综合练习【练习1】已知函数，若存在，使得，则实数的值为______．【练习2】已知函数，若、，，使得成立，则的取值范围是（    ）．A． B． C． D．或【练习3】已知函数，，若存在实数，使得成立，则实数的取值范围为（   ）A． B．[来源:学科网]C． D．【练习4】已知函数,.（1）函数的图象与的图象无公共点,求实数的取值范围；（2）是否存在实数,使得对任意的,都有函数的图象在的图象的下方？若存在,请求出整数的最大值；若不存在,请说理由.（参考数据：,,）.                            四、函数中恒成立与存在性的综合问题                [来源:Z§xx§k.Com]1.例题【例1】已知函数，，，总，使得成立，则实数的取值范围是____________. 【例2】已知函数f (x)＝x2－2ax＋1，g(x)＝，其中a>0，x≠0.(1) 对任意，都有恒成立，求实数的取值范围；(2) 对任意，任意，都有恒成立，求实数的取值范围；(3) 对任意，存在，使成立，求实数的取值范围；(4) 存在，任意，使成立，求实数的取值范围．              巩固提升综合练习【练习1】已知二次函数 的图象过点 若对任意的 ，存在 ，使得 ，求 的取值范围.           【练习2】 已知函数 ．[来源:Z_xx_k.Com]（1）若曲线 在 和 处的切线互相平行，求 的值；（2）求 的单调区间；（3）设 ，若对 ，均存在 ，使得 ，求 的取值范围             五、课后自我检测                         1．已知函数的图象在点（为自然对数的底数）处的切线的斜率为．(1)求实数的值；(2)若对任意成立,求实数的取值范围.      2.已知函数,,其中且,．(1)若,且时,的最小值是－2,求实数的值；(2)若,且时,有恒成立,求实数的取值范围.     3.设函数,其中,若存在唯一的整数,使得,则的取值范围是（ ）A．          B．        C．           D． 4.已知函数f(x)＝x3－ax2＋10,若在区间[1,2]内至少存在一个实数x,使得f(x)<0成立,求实数a的取值范围．      5.若不等式对任意恒成立,求实数x的取值范围.       6.若不等式对任意的恒成立,则的取值范围是（    ）A.     B.     C.     D.  7.已知函数,若关于的不等式恰有个整数解,则实数的最大值是（     ）A.     B.     C.     D.  8.已知函数,若对任意, 恒成立,则实数的取值范围是（   ）A.     B.    C.     D.  9.已知函数,若有且只有两个整数, 使得,且,则的取值范围是（   ）A.     B.     C.     D.  [来源:学。科。网]10.已知对任意的，总存在唯一的，使得成立（为自然对数的底数），则实数的取值范围是(    )A．     B．     C．     D．