方法技巧专题24 统计图表的应用-2022年高考数学满分之路方法技巧篇

这是一份方法技巧专题24 统计图表的应用-2022年高考数学满分之路方法技巧篇，文件包含方法技巧专题24统计图表的应用解析版docx、方法技巧专题24统计图表的应用原卷版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。
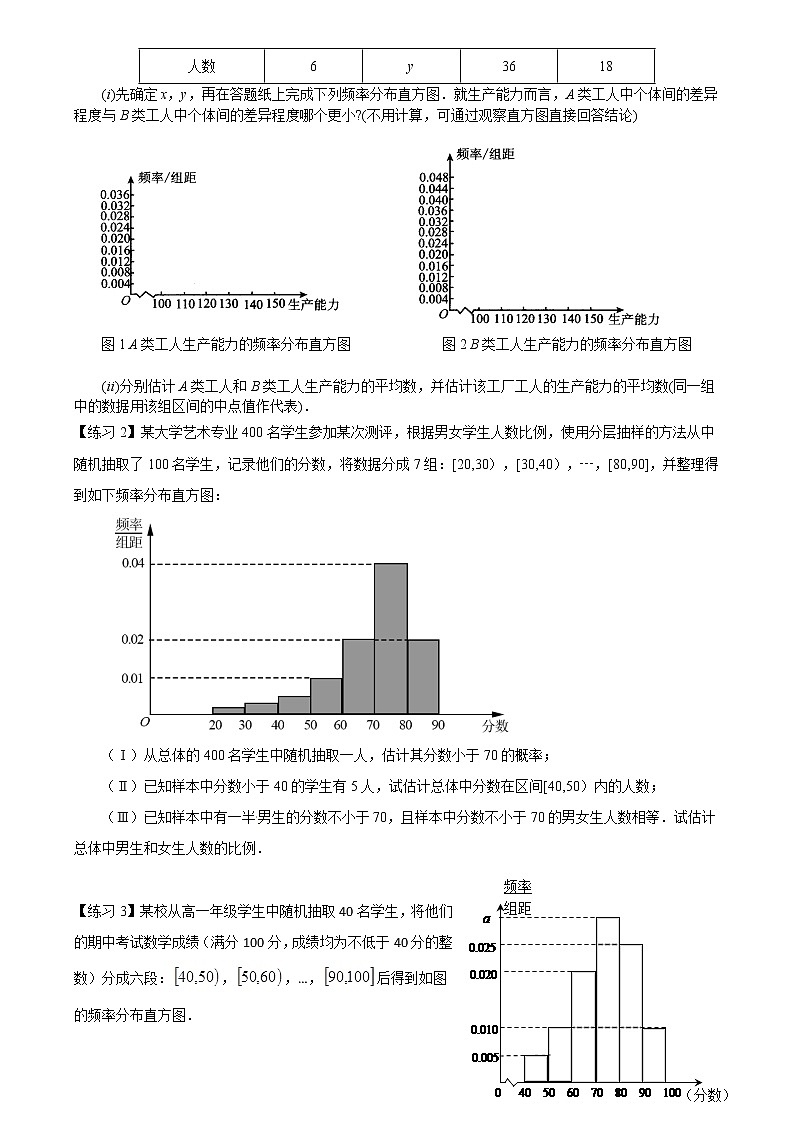
 方法技巧专题24  统计图表的应用学生篇             一、统计图表的应用知识框架                      统计图表的应用题型分析                  【一】频率分布直方图 1.例题【例1】 我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行了调查．通过抽样，获得了某年100位居民每人的月均用水量(单位：吨)．将数据按照[0,0.5)，[0.5，1)，…，[4,4.5]分成9组，制成了如图所示的频率分布直方图．     (1)求直方图中a的值；(2)设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由；(3)估计居民月均用水量的中位数．【例2】(2019年高考全国Ⅲ卷文数)为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A，B两组，每组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液．每只小鼠给服的溶液体积相同、摩尔浓度相同．经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比．根据试验数据分别得到如下直方图：记C为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P（C）的估计值为0.70．（1）求乙离子残留百分比直方图中a，b的值；（2）分别估计甲、乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）．2.巩固提升综合练习【练习1】某工厂有工人1000名，其中250名工人参加过短期培训(称为A类工人)，另外750名工人参加过长期培训(称为B类工人)，现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人，调查他们的生产能力(此处生产能力指一天加工的零件数)．(Ⅰ)求甲、乙两工人都被抽到的概率，其中甲为A类工人，乙为B类工人；(Ⅱ)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2．表1：生产能力分组[100，110)[110，120)[120，130)[130，140)[140，150)人数48x53表2生产能力分组[110，120)[120，130)[130，140)[140，150)人数6y3618(i)先确定x，y，再在答题纸上完成下列频率分布直方图．就生产能力而言，A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算，可通过观察直方图直接回答结论)        图1 A类工人生产能力的频率分布直方图             图2 B类工人生产能力的频率分布直方图 (ii)分别估计A类工人和B类工人生产能力的平均数，并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表)．【练习2】某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20,30），[30,40），┄，[80,90]，并整理得到如下频率分布直方图：（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40,50）内的人数；（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例． 【练习3】某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：，，…，后得到如图的频率分布直方图． （1）求图中实数的值；（2）若该校高一年级共有学生640人，试估计该校高一年级期中考试数学成绩不低于60分的人数；（3）若从数学成绩在与两个分数段内的学生中随机选取两名学生，求这两名学生的数学成绩之差的绝对值不大于10的概率． 【练习4】某市民用水拟实行阶梯水价．每人用水量中不超过立方米的部分按4元/立方米收费，超出立方米的部分按10元/立方米收费．从该市随机调查了10000位居民，获得了他们某月的用水量数据，整理得到如下频率分布直方图：（Ⅰ）如果为整数，那么根据此次调查，为使80%以上居民在该月的用水价格为4元/立方米，至少定为多少？（Ⅱ）假设同组中的每个数据用该组区间的右端点值代替．当=3时，估计该市居民该月的人均水费． 【二】茎叶图的应用 1.例题【例1】如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据（单位：件）.若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为A.  3，5         B.  5，5        C.  3，7        D.  5，7 【例2】某学校A、B两个班的兴趣小组在一次对抗赛中的成绩如茎叶图所示,通过茎叶图比较两个班兴趣小组成绩的平均值及标准差.①A班兴趣小组的平均成绩高于B班兴趣小组的平均成绩;②B班兴趣小组的平均成绩高于A班兴趣小组的平均成绩;③A班兴趣小组成绩的标准差大于B班兴趣小组成绩的标准差;④B班兴趣小组成绩的标准差大于A班兴趣小组成绩的标准差.其中正确结论的编号为(　　)A.①④     B.②③    C.②④     D.①③ 【例3】随机抽取某中学甲、乙两班各10名同学，测量他们的身高(单位：cm)，获得身高数据的茎叶图(1)根据茎叶图判断哪个班的平均身高较高；(2)计算甲班的样本方差；(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高为176cm的同学被抽中的概率． 2.巩固提升综合练习【练习1】 某兄弟俩都推销某一小家电,现抽取他们其中8天的销售量(单位:台),得到的茎叶图如图所示,已知弟弟的销售量的平均数为34,哥哥的销售量的中位数比弟弟的销售量的众数大2,则x+y的值为　　　　. 【练习2】从甲、乙两种树苗中各抽测了株树苗的高度，其茎叶图如图所示．根据茎叶图，下列描述正确的是(     ) A．甲种树苗的高度的中位数大于乙种树苗高度的中位数，且甲种树苗比乙种树苗长得整齐B．甲种树苗的高度的中位数大于乙种树苗高度的中位数，但乙种树苗比甲种树苗长得整齐C．乙种树苗的高度的中位数大于甲种树苗高度的中位数，且乙种树苗比甲种树苗长得整齐D．乙种树苗的高度的中位数大于甲种树苗高度的中位数，但甲种树苗比乙种树苗长得整齐【练习3】甲、乙两名同学在 6 次数学考试中，所得成绩用茎叶图表示如下，若甲、乙两人这 6 次考试的平均成绩分别用 表示，则下列结论正确的是（   ） A． ，且甲成绩比乙成绩稳定 B．B． ，且乙成绩比甲成绩稳定C． ，且甲成绩比乙成绩稳定 D．D．，且乙成绩比甲成绩稳定  【三】其它类型的统计图表  频率分布折线图：连结频率分布直方图各个长方形上边的中点，就得到频率分布折线图．总体密度曲线：随着样本容量的增加，分组的组距不断缩小，相应的频率分布折线图就会越来越接近于一条光滑曲线，这条光滑曲线就叫做总体密度曲线．总体密度曲线精确地反映了一个总体在各个区域内取值的规律．散点图：两个变量的关系可通过它们所对应的点在平面上表现出来，这些点对应的图形叫做散点图． 【例1】某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量(单位：万人)的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是(　　)A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7,8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳【例2】已知随机变量，其正态分布密度曲线如图所示，若向长方形中随机投掷1点，则该点恰好落在阴影部分的概率为（   ）    附：若随机变量，则，.A．0.1359 B．0.7282 C．0.8641 D．0.93205 【例3】 图1是某县参加2007年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A1、A2、…、Am(如A2表示身高(单位：cm)在[150，155)内的学生人数)．图2是统计图1中身高在一定范围内学生人数的一个算法流程图．现要统计身高在160～180cm(含160cm，不含180cm)的学生人数，那么在流程图中的判断框内应填写的条件是______．     图1                           图2 2.巩固提升综合练习【练习1】是衡量空气质量的重要指标，我国采用世卫组织的最宽值限定值，即日均值在以下空气质量为一级，在空气量为二级，超过为超标．如图是某地12月1日至10日的（单位：)的日均值，则下列说法不正确的是（   ）A．这天中有天空气质量为一级B．从日到日日均值逐渐降低C．这天中日均值的中位数是D．这天中日均值最高的是月日 【练习2】 某学校为了了解本校学生的上学方式,在全校范围内随机抽查部分学生,了解到上学方式主要有:A结伴步行,B自行乘车,C家人接送,D其他方式,并将收集的数据整理绘制成如下两幅不完整的统计图.根据图中信息,可知本次抽查的学生中A类人数是(　　)A.30   B.40     C.42      D.48【练习3】某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图．图中A点表示十月的平均最高气温约为15℃，B点表示四月的平均最低气温约为5℃．下面叙述不正确的是 A．各月的平均最低气温都在0℃以上          B．七月的平均温差比一月的平均温差大C．三月和十一月的平均最高气温基本相同      D．平均最高气温高于20℃的月份有5个                                 三、课后自我检测                         1．某单位200名职工的年龄分布情况如图，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1－200编号，并按编号顺序平均分为40组(1－5号，6－10号，…，196－200号)．若第5组抽出的号码为22，则第8组抽出的号码应是______，若用分层抽样方法，则40岁以下年龄段应抽取______人．    2．某位教师2017年的家庭总收入为80 000元,各种用途占比统计如下面的折线图.2018年收入的各种用途占比统计如下面的条形图,已知2018年的就医费用比2017年增加了4 750元,则该教师2018年的家庭总收入为(　　) [来源:学*科*网]   A.100 000元        B.95 000元       C.90 000元       D.85 000元3．(2018全国卷Ⅰ)某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例．得到如下饼图：则下面结论中不正确的是（   ）A．新农村建设后，种植收入减少           B．新农村建设后，其他收入增加了一倍以上C．新农村建设后，养殖收入增加了一倍D．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半 4．某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20)， [20，22.5)， [22.5,25)，[25，27.5)，[27.5，30)．根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是（    ）A．56    B．60    C．120        D．1405．高三年级267位学生参加期末考试，某班37位学生的语文成绩，数学成绩与总成绩在全年级中的排名情况如下，甲、乙、丙为该班三位学生．从这次考试成绩看，①在甲、乙两人中，其语文成绩名次比其总成绩名次靠前的学生是       ；②在语文和数学两个科目中，丙同学的成绩名次更靠前的科目是         ． 6．2019年春节期间，我国高速公路继续执行“节假日高速免费政策”.某路桥公司为掌握春节期间车辆出行的高峰情况，在某高速收费点处记录了大年初三上午9:20～10:40这一时间段内通过的车辆数，统计发现这一时间段内共有600辆车通过该收费点，它们通过该收费点的时刻的频率分布直方图如图所示，其中时间段9:20～9：40记作区间，9:40～10:00记作，10:00～10:20记作，10:20～10:40记作.比方：10点04分，记作时刻64. （1）估计这600辆车在9:20～10:40时间段内通过该收费点的时刻的平均值（同一组中的数据用该组区间的中点值代表）；（2）为了对数据进行分析，现采用分层抽样的方法从这600辆车中抽取10辆，再从这10辆车中随机抽取4辆，记为9:20～10:00之间通过的车辆数，求的分布列与数学期望；（3）由大数据分析可知，车辆在春节期间每天通过该收费点的时刻服从正态分布，其中可用这600辆车在9:20～10:40之间通过该收费点的时刻的平均值近似代替，可用样本的方差近似代替（同一组中的数据用该组区间的中点值代表），已知大年初五全天共有1000辆车通过该收费点，估计在9:46～10:40之间通过的车辆数（结果保留到整数）.参考数据：若，则，，.7．（2018全国卷Ⅰ）某家庭记录了未使用节水龙头50天的日用水量数据（单位：）和使用了节水龙头50天的日用水量数据，得到频数分布表如下：未使用节水龙头50天的日用水量频数分布表日用水量频数13249265使用了节水龙头50天的日用水量频数分布表日用水量频数1513[来源:学科网]10165(1)在下图中作出使用了节水龙头50天的日用水量数据的频率分布直方图：(2)估计该家庭使用节水龙头后，日用水量小于0.35 的概率；(3)估计该家庭使用节水龙头后，一年能节省多少水？（一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表．）8．我国已进入新时代中国特色社会主义时期，人民生活水平不断提高．某市随机统计了城区若干户市民十月人均生活支出比九月人均生活支出增加量（记为P元）的情况，并根据统计数据制成如图频率分布直方图．（1）根据频率分布直方图估算P的平均值；（2）若该市城区有4户市民十月人均生活支出比九月人均生活支出分别增加了42元，50元，52元，60元，从这4户中随机抽取2户，求这2户P值的和超过100元的概率．从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位：mm)，结果如下：甲品种：271  273  280  285  285  287  292  294  295  301  303  303  307308  310  314  319  323  325  325  328  331  334  337  352乙品种：284  292  295  304  306  307  312  313  315  315  316  318  318320  322  322  324  327  329  331  333  336  337  343  356由以上数据设计了如下茎叶图根据以上茎叶图，对甲、乙两品种棉花的纤维长度作比较，写出两个统计结论：①___________________________________________________________________________________________________________________________________________________；②___________________________________________________________________________________________________________________________________________________．