（全国通用）备战中考数学一轮复习专题讲义+强化训练 第十八讲 等腰三角形（强化训练）

这是一份（全国通用）备战中考数学一轮复习专题讲义+强化训练 第十八讲 等腰三角形（强化训练），文件包含全国通用备战2022年中考数学一轮复习专题第十八讲等腰三角形强化训练解析版docx、全国通用备战2022年中考数学一轮复习专题第十八讲等腰三角形强化训练原卷版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
备战2022年中考数学一轮复习专题讲义+强化训练（全国通用）
第十八讲 等腰三角形
考点一 等腰三角形的判定与性质 2
考点二 等边三角形的判定与性质 8
考点三 角平分线的判定与性质 13















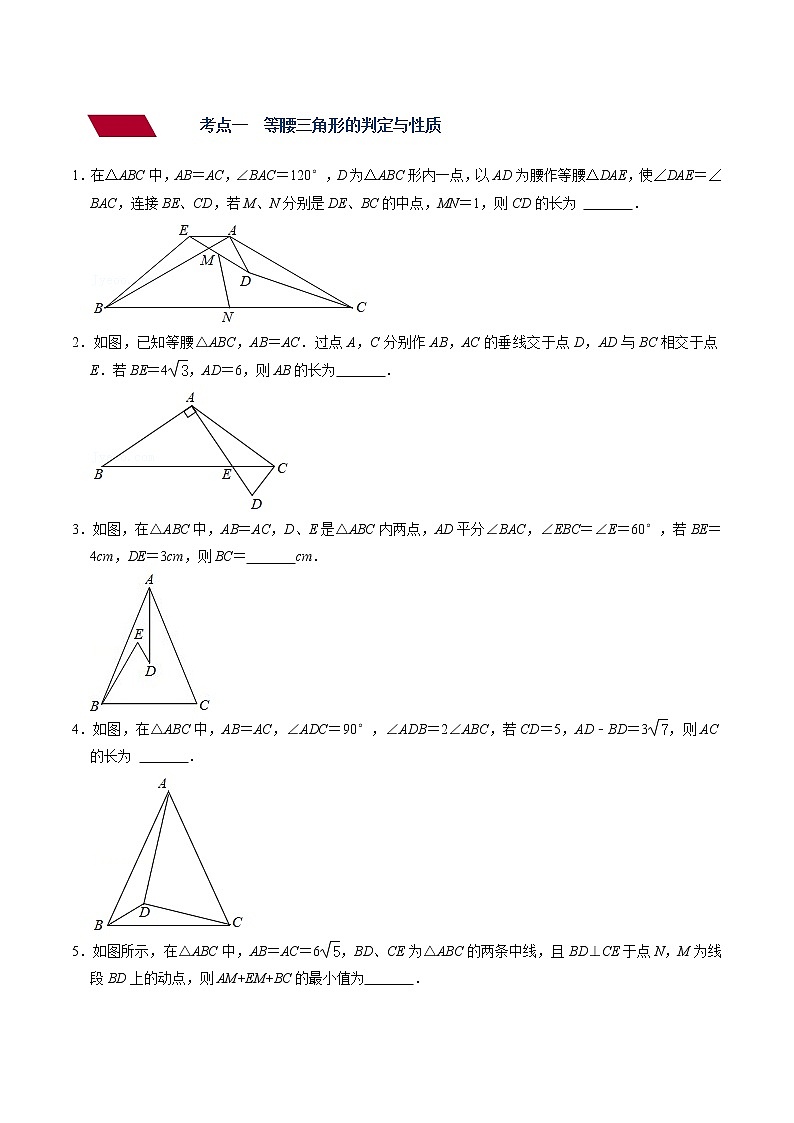
考点一 等腰三角形的判定与性质

1．在△ABC中，AB＝AC，∠BAC＝120°，D为△ABC形内一点，以AD为腰作等腰△DAE，使∠DAE＝∠BAC，连接BE、CD，若M、N分别是DE、BC的中点，MN＝1，则CD的长为 　2　．

【解答】解：如图，连接BD，取BD的中点F，连接FM，FN，

∵∠BAC＝∠EAD，
∴∠BAC﹣∠BAD＝∠EAD﹣∠BAD，
即∠BAE＝∠CAD，
在△AEB和△ADC中，
，
∴△AEB≌△ADC（SAS），
∴BE＝CD，
∵M是ED的中点，F是BD的中点，
∴FM是△BED的中位线，
∴FM＝BE，FM∥BE，
∴∠DFM＝∠EBD，
同理得FN＝CD，FN∥CD，
∴FM＝FN，∠FNB＝∠DCB，
∵∠DFN＝∠DBC+∠FNB＝∠DBC+∠DCB，
∴∠MFN＝∠DFM+∠DFN＝∠EBD+∠DBC+∠DCB＝180°﹣120°＝60°，
∴△FMN是等边三角形，
∴MN＝FN＝1，
∴CD＝2．
故答案为：2．
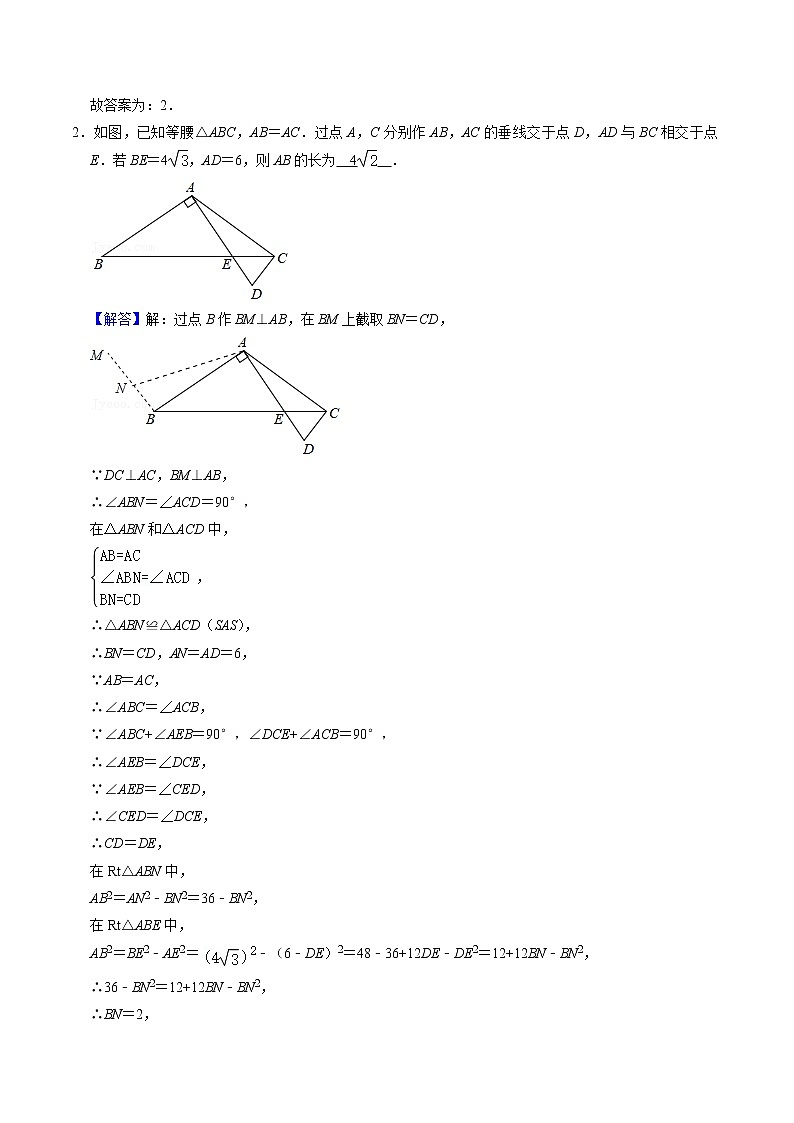
2．如图，已知等腰△ABC，AB＝AC．过点A，C分别作AB，AC的垂线交于点D，AD与BC相交于点E．若BE＝4，AD＝6，则AB的长为　4　．

【解答】解：过点B作BM⊥AB，在BM上截取BN＝CD，

∵DC⊥AC，BM⊥AB，
∴∠ABN＝∠ACD＝90°，
在△ABN和△ACD中，
，
∴△ABN≌△ACD（SAS），
∴BN＝CD，AN＝AD＝6，
∵AB＝AC，
∴∠ABC＝∠ACB，
∵∠ABC+∠AEB＝90°，∠DCE+∠ACB＝90°，
∴∠AEB＝∠DCE，
∵∠AEB＝∠CED，
∴∠CED＝∠DCE，
∴CD＝DE，
在Rt△ABN中，
AB2＝AN2﹣BN2＝36﹣BN2，
在Rt△ABE中，
AB2＝BE2﹣AE2＝﹣（6﹣DE）2＝48﹣36+12DE﹣DE2＝12+12BN﹣BN2，
∴36﹣BN2＝12+12BN﹣BN2，
∴BN＝2，
∴AB＝＝＝＝4，
故答案为：4．
3．如图，在△ABC中，AB＝AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC＝∠E＝60°，若BE＝4cm，DE＝3cm，则BC＝　7　cm．

【解答】解：延长ED交BC于M，延长AD交BC于N，作DF∥BC，
∵AB＝AC，AD平分∠BAC，
∴AN⊥BC，BN＝CN，
∵∠EBC＝∠E＝60°，
∴△BEM为等边三角形，
∴△EFD为等边三角形，
∵BE＝4cm，DE＝3cm，
∴DM＝1cm，
∵△BEM为等边三角形，
∴∠EMB＝60°，
∵AN⊥BC，
∴∠DNM＝90°，
∴∠NDM＝30°，
∴NM＝cm，
∴BN＝cm，
∴BC＝2BN＝7cm，
故答案为7．

4．如图，在△ABC中，AB＝AC，∠ADC＝90°，∠ADB＝2∠ABC，若CD＝5，AD﹣BD＝3，则AC的长为 　　．

【解答】解：将△ADB绕点A逆顺时针旋转到△AEC，连接DE，
由题意可得：∠ADB＝∠AEC＝2∠ABC，∠DAB＝∠EAC，
∴∠EAD＝∠BAC，
又∵AE＝AD，AB＝AC，
∴，
∵∠EAC＝∠DAB，
∴∠EAD＝∠BAC，
∴△AED∽△ACB，
∴∠AED＝∠ADE＝∠CED＝∠ABC＝∠ADB＝∠AEC，
∵∠ADC＝∠ADE+∠CDE＝90°，
∴∠CED+∠CDE＝90°，
∴∠ECD＝90°，
过点D作DF⊥AE，
∵∠CED＝∠AED，
∴DC＝DF＝5，
在△EFD和△ECD中，
，
∴△EFD≌△ECD （AAS），
∴CE＝EF，
∵AD﹣BD＝3，
设BD＝x，
∴CE＝EF＝x，AD＝AE＝x+3，
∴AF＝3，
在△AFD中，
AD＝＝＝，
∴AC＝AB＝＝＝．
故答案为：．

5．如图所示，在△ABC中，AB＝AC＝6，BD、CE为△ABC的两条中线，且BD⊥CE于点N，M为线段BD上的动点，则AM+EM+BC的最小值为　3+6　．

【解答】解：连接DE．
∵AB＝AC，
∴∠ABC＝∠ACB，
∵BE＝AB，DC＝AC，
∴BE＝CD，
∵BC＝CB，
∴△EBC≌△DCB（SAS），
∴∠ECB＝∠DBC，EC＝BD，
∴BN＝CN，
∴EN＝DN，
∵BD⊥EC，
∴△EDN，△BCN都是等腰直角三角形，
∵AE＝EB，AD＝DC，
∴DE∥BC，DE＝BC，
∴＝＝，
∴CN＝2EN，
∴BN＝2EN，
∵AE＝BE＝3，
∴EN＝3，BN＝6，
∴BN＝CN＝6，
∴BC＝6，
作点A关于直线BD的对称点H，连接EH交BD于M，连接AM，此时AM+EM的值最小，最小值＝线段EH的长，过点H作HT⊥AB于T，延长BD交AH于J，如图所示．
∵AJ∥EN，AE＝EB，
∴BN＝NJ＝6，
∴AJ＝JH＝2EN＝6，
∵S△ABH＝•AB•HT＝•AH•BJ，
∴HT＝＝，
∴AT＝＝＝，
∴ET＝AE﹣AT＝3﹣＝，
∴EH＝＝＝3，
∴AM+EM+BC的最小值为3+6．
故答案为3+6．


考点二 等边三角形的判定与性质

6．如图，在正三角形ABC中，D，E分别为边BC，AC上的点，AD，BE相交于点F，连接CF，若AF＝4，∠FBC＝∠DAB，则S△ACF＝　4　．

【解答】解：如图，将△ABF绕A逆时针旋转60°，得到△ACG，连接EG，作AH⊥BE于点H，

∵△BAD≌△CAG，
∴AF＝AG＝4，∠FAG＝60°，
设∠DBF＝∠BAD＝α，
则60°+α＝∠AEH，
∴∠CDF+∠CEF＝120°，
∴∠DCE+∠DFE＝120°，
∴∠AFG＝60°，
E，F，G三点共线，
∴△AFG是等边三角形，
∵∠ABF＝∠ACG＝60°﹣α，
∠ADC＝60°+α，
∴∠ADC+∠GCD＝60°+α+60°+60°﹣α＝180°，
∴AD∥CG，
∴S△CGF＝S△CGA，
∴S△CEF＝S△AGE，
∴S△ACF＝S△AFG，
根据等边三角形的性质得H是FG的中点，
∴HF＝2，
∴AH＝，
∴，
∴，
故答案为4．
7．如图，AB＝6，点O在线段AB上，AO＝2，⊙O的半径为1．点P是⊙O上一动点，以BP为一边作等边△BPQ，则AQ的最小值为 　　．

【解答】解：如图，以BO为边作等边△BOC，连接CQ，AC，

∵△BOC和△BPQ都是等边三角形，
∴∠OBC＝∠PBQ，OB＝BC，BP＝BQ，
∴∠OBP＝∠CBQ，
在△OBP和△CBQ中，
，
∴△OBP≌△CBQ（SAS），
∴OP＝CQ＝1，
∵AB＝6，AO＝2，
∴OB＝4，
∵CH⊥OB于H，
∴OH＝2，CH＝tan60°×OH＝2，
在Rt△ACH中，由勾股定理得：AC＝，
∵AC﹣CQ≤AQ，
∴AQ≥2﹣1，
∴AQ的最小值为：2，
故答案为：2．
8．如图，在四边形ABCD中，AB＝2，BC＝BD，∠ADC＝150°，∠DCB＝60°，则AC的最大值是　+1　．

【解答】解：如图，以AB为边作等边△ABE，连结EC，

∴AB＝BE＝AE，∠ABE＝∠EAB＝∠AEB＝60°，
∵BC＝BD，∠DCB＝60°，
∴△DCB为等边三角形，
∴BD＝BC＝CD，∠DCB＝∠CDB＝∠DCB＝60°，
∵∠ADC＝150°，
∴∠ADB＝∠ADC﹣∠CDB＝150°﹣60°＝90°，
在△ABD和△EBC中，
，
∴△ABD≌△EBC（SAS），
∴∠ADB＝∠ECB＝90°，
在△EBC中，EB＝AB＝2，∠ECB＝90°，
以BE为直径作⊙O，则半径为BE＝1，
∴动点C在以BE为直径的⊙O上，连结AO并延长交⊙O于点C′，
∴AC≤AC′＝AO+OC′＝AO+1，
在等边△ABE中，AB＝2，O为BE的中点，
∴AO＝＝＝，
∴AC′＝+1，
即AC的最大值为+1，
故答案为：+1．
9．如图，已知等边三角形ABC的高为7cm，P为△ABC内一点，PD⊥AB于点D，PE⊥AC于点E，PF⊥BC于点F．则PD+PE+PF＝　7cm　．

【解答】解：连接PA、PB、PC，作AB边上的高CG，如图所示：
∵S△ABP+S△BCP+S△ACP＝S△ABC，
∴AB•PD+BC•PF+AC•PE＝AB•CG，
∵△ABC是等边三角形，
∴AB＝BC＝AC，
∴AB（PE+PF+PD）＝AB•CG，
∴PE+PD+PF＝CG＝7cm
故答案为：7cm；

考点三 角平分线的判定与性质

10．如图，∠ABC、∠ACE的平分线BP、CP交于点P，PF⊥BD，PG⊥BE，垂足分别为F、G，下列结论：①S△ABP：S△BCP＝AB：BC；②∠APB+∠ACP＝90°；③∠ABC+2∠APC＝180°，其中正确的结论有（　　）

A．0个 B．1个 C．2个 D．3个
【解答】解：∵PB平分∠ABC，PF⊥BD，PG⊥BE，
∴PF＝PG，
∴S△ABP：S△BCP＝AB•PF：BC•PG＝AB：BC，故①正确；
过P作PH⊥AC于H，
∵PC平分∠ACE，
∴PH＝PG，
∴PF＝PH，
∴PA平分∠CAF，
∵BP平分∠ABC，
∴∠CAF＝∠ABC+∠ACB＝2∠PAF，∠PAF＝∠ABC+∠APB，
∴∠ACB＝2∠APB，
∵∠ACB+∠ACE＝180°，
∴＝∠APB+∠ACP＝90°，故②正确；
∵PF⊥AB，PG⊥BC，
∴∠ABC+90°+∠FPG+90°＝360°，
∴∠ABC+∠FPG＝180°，
在Rt△PAF和Rt△PAH中，
，
∴Rt△PAF≌Rt△PAH（HL），
∴∠APF＝∠APG，
同理：Rt△PCH≌Rt△PCG（HL），
∴∠CPH＝∠CPG，
∴∠FPG＝2∠APC，
∴∠ABC+2∠APC＝180°，故③正确；
故选：D．

11．如图，△ABC中，AD⊥BC交BC于D，AE平分∠BAC交BC于E，F为BC的延长线上一点，FG⊥AE交AD的延长线于G，AC的延长线交FG于H，连接BG，下列结论：①∠DEA＝∠AGH；②∠DAE＝（∠ABD﹣∠ACE）；③∠AGH＝∠BAE+∠ACB；④S△AEB：S△AEC＝AB：AC，其中正确的结论有（　　）个．

A．1 B．2 C．3 D．4
【解答】解：如图，AE交GF于M，

①∵AD⊥BC，FG⊥AE，
∴∠ADE＝∠AMF＝90°，
∴∠DEA+∠DAE＝∠AGH+∠GAM＝90°，
∴∠DEA＝∠AGH，故①正确；
②∵AE平分∠BAC交BC于E，
∴∠EAC＝∠BAC，
∠DAE＝90°﹣∠AED，
＝90°﹣（∠ACE+∠EAC），
＝90°﹣（∠ACE+∠BAC），
＝（180°﹣2∠ACE﹣∠BAC），
＝（∠ABD﹣∠ACE），
故②正确；
③∵∠DAE＝∠F，∠FDG＝∠FME＝90°，
∴∠AGH＝∠MEF，
∵∠MEF＝∠CAE+∠ACB，
∴∠AGH＝∠CAE+∠ACB，
∴∠AGH＝∠BAE+∠ACB，故④正确；
④∵AE平分∠BAC交BC于E，
∴点E到AB和AC的距离相等，
∴S△AEB：S△AEC＝AB：AC，故③正确；
故选：D．
12．如图，△ABC中，∠ACF、∠EAC的角平分线CP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF．则下列结论中正确的个数（　　）
①BP平分∠ABC；②∠ABC+2∠APC＝180°；③∠CAB＝2∠CPB；④S△PAC＝S△MAP+S△NCP．

A．1个 B．2个 C．3个 D．4个
【解答】解：过P作PQ⊥AC于Q，

∵∠ACF、∠EAC的角平分线CP、AP交于点P，PM⊥BE，PN⊥BF，
∴PM＝PQ，PQ＝PN，
∴PM＝PN，
∴P在∠ABC的角平分线上，即BP平分∠ABC，故①正确；
∵PM⊥AB，PN⊥BC，PQ⊥AC，
∴∠PMA＝∠PQA＝90°，∠PQC＝∠PNC＝90°，
在Rt△PMA和Rt△PQA中，
，
∴Rt△PMA≌Rt△PQA（HL），
∴∠MPA＝∠QPA，
同理Rt△PQC≌Rt△PNC，
∴∠QPC＝∠NPC，
∵∠PMA＝∠PNC＝90°，
∴∠ABC+∠MPN＝360°﹣90°﹣90°＝180°，
∴∠ABC+2∠APC＝180°，故②正确；
∵PC平分∠FCA，BP平分∠ABC，
∴∠FCA＝∠ABC+∠CAB＝2∠PCN，
又∵∠PCN＝∠ABC+∠CPB，
∴∠ABC+∠CAB＝2（∠ABC+∠CPB），
∴∠CAB＝2∠CPB，故③正确；
∵Rt△PMA≌Rt△PQA，Rt△PQC≌Rt△PNC，
∴S△PAC＝S△MAP+S△NCP，故④正确；
即正确的个数是4，
故选：D．
13．如图，Rt△ACB中，∠ACB＝90°，∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P，分别交AC和BC的延长线于E，D．过P作PF⊥AD交AC的延长线于点H，交BC的延长线于点F，连接AF交DH于点G．则下列结论：①∠APB＝45°；②PF＝PA；③BD﹣AH＝AB；④DG＝AP+GH．其中正确的有（　　）个

A．1 B．2 C．3 D．4
【解答】解：①∵∠ABC的角平分线BE和∠BAC的外角平分线，
∴∠ABP＝∠ABC，
∠CAP＝（90°+∠ABC）＝45°+∠ABC，
在△ABP中，∠APB＝180°﹣∠BAP﹣∠ABP，
＝180°﹣（45°+∠ABC+90°﹣∠ABC）﹣∠ABC，
＝180°﹣45°﹣∠ABC﹣90°+∠ABC﹣∠ABC，
＝45°，故本小题正确；
②∵PF⊥AD，∠APB＝45°（已证），
∴∠APB＝∠FPB＝45°，
∵PB为∠ABC的角平分线，
∴∠ABP＝∠FBP，
在△ABP和△FBP中，，
∴△ABP≌△FBP（ASA），
∴AB＝BF，AP＝PF；故②正确；
③∵∠ACB＝90°，PF⊥AD，
∴∠FDP+∠HAP＝90°，∠AHP+∠HAP＝90°，
∴∠AHP＝∠FDP，
∵PF⊥AD，
∴∠APH＝∠FPD＝90°，
在△AHP与△FDP中，，
∴△AHP≌△FDP（AAS），
∴DF＝AH，
∵BD＝DF+BF，
∴BD＝AH+AB，
∴BD﹣AH＝AB，故③小题正确；
④∵PF⊥AD，PD＝PH，∠ACB＝90°，
∴△DPH为等腰直角三角形，
∴∠PDH＝45°，
∵∠PAF＝45°，
∴AG⊥DH，
∴△ADG与△FGH都是等腰直角三角形，
∴DG＝AG，GH＝GF，
∴DG＝GH+AF，
∵AF＞AP，
∴DG＝AP+GH不成立，故本小题错误，
综上所述①②③正确．
故选：C．