（全国通用）2022年中考数学命题点及重难题型分类突破练 类型二 与圆切线有关的证明与计算（原卷版+解析版）

这是一份（全国通用）2022年中考数学命题点及重难题型分类突破练 类型二 与圆切线有关的证明与计算（原卷版+解析版），文件包含全国通用2022年中考数学命题点及重难题型分类突破练类型二与圆切线有关的证明与计算解析版docx、全国通用2022年中考数学命题点及重难题型分类突破练类型二与圆切线有关的证明与计算原卷版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
类型二与切线有关的证明与计算
1.如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙O交于点D，连结OD．
若∠C＝50°，则∠AOD的度数（ ）
A．40° B．50° C．80° D．100°


【答案】C
【解析】∵AC是⊙O的切线，∴AC⊥AB．∵∠C＝50°，∴∠B＝90°－∠C＝40°．∵OB＝OD，∴∠B＝∠ODB＝40°．∴∠AOD＝∠B＋∠ODB＝80°．故选C．
2.如图，等腰直角三角形ABC中，∠C＝90°，AC＝，以点C为圆心画弧与斜边AB相切于点D，交AC于点E，交BC于点F，则图中阴影部分的面积是（　　）

A．1﹣ B． C．2﹣ D．1+
【解析】连接CD，如图，∵AB是圆C的切线，∴CD⊥AB，
∵△ABC是等腰直角三角形，∴AB＝AC＝×＝2，∴CD＝AB＝1，
∴图中阴影部分的面积＝S△ABC﹣S扇形ECF＝××﹣＝1﹣．故选：A．

3.如图，在Rt△ABC中，∠C＝90°，AC＝BC，点O在AB上，经过点A的⊙O与BC相切于点D，交AB于点E，若CD＝，则图中阴影部分面积为（　　）

A．4﹣ B．2﹣ C．2﹣π D．1﹣
【解析】连接OD，过O作OH⊥AC于H，如图，
∵∠C＝90°，AC＝BC，
∴∠B＝∠CAB＝45°，
∵⊙O与BC相切于点D，
∴OD⊥BC，
∴四边形ODCH为矩形，
∴OH＝CD＝，
在Rt△OAH中，∠OAH＝45°，
∴OA＝OH＝2，
在Rt△OBD中，∵∠B＝45°，
∴∠BOD＝45°，BD＝OD＝2，
∴图中阴影部分面积＝S△OBD﹣S扇形DOE
＝×2×2﹣
＝2﹣π．
故选：B．
4.已知△ABC内接于⊙O，AB=AC，∠ABC的平分线与⊙O交于点D，与AC交于点E，连接CD并延长与⊙O过点A的切线交于点F，记∠BAC=.
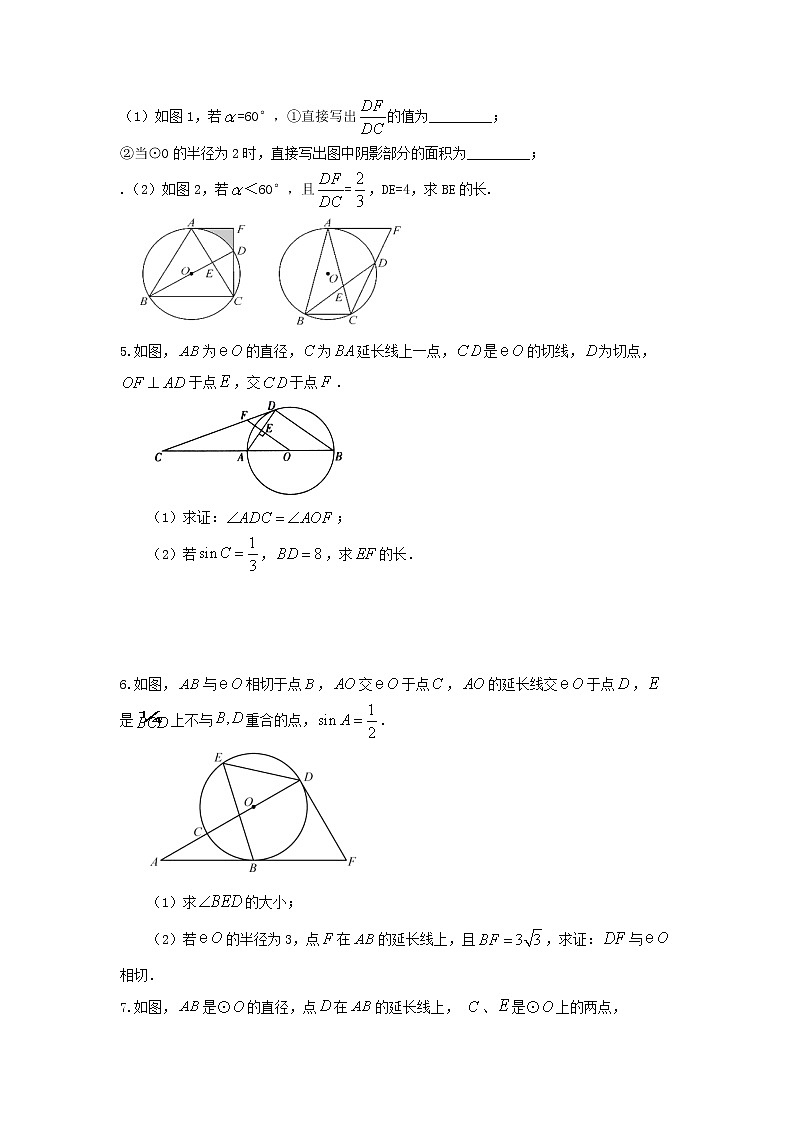
（1）如图1，若=60°，①直接写出的值为_________；
②当⊙O的半径为2时，直接写出图中阴影部分的面积为_________；
.（2）如图2，若＜60°，且=，DE=4，求BE的长.

【解析】本题考查圆的有关知识和等边三角形知识以及全等三角形和相似三角形知识.
（1） ①利用等边三角形和角平分线性质可得到=.再利用切线性质可得到∠DAF＝30°.利用30°直角边等于斜边的一半得=.②利用三角形ADF的面积减去弓形AD的面积即可.

（2） 连接AD，证明△ADF与△ADE全等，得到DF=DE=4,再利用已知的比求出DC，再结合相似三角形可求出BE.
{答案}解：（1）①连接AD,AO.
在△ABC中，AB=AC,∠BAC＝＝60°，
∴△ABC是等边三角形.
∴∠ABC=∠ACB=∠BAC=60°
∵BD平分∠ABC
∴∠ABD=∠CBD=∠ACD=∠CAD=30°,AD=CD
∴△AOD是等边三形
∴∠OAD=∠AOD=60°
∵AF是的切线，AO是半径
∴∠OAF=90°,∠FAD=30°,∠CAF=60°
在△ACF中,∠F＝180°－∠ACD-∠CAF=180°-30°-60°=90°.
∴在Rt△ACF中,∠F=90°,∠FAD=30°,
,
∴.故填.
②由①题知，∠AOD＝60°,∠DAF=30°，
∵AO=AD=2,
∴DF=1,AF=.

∴弓形AD的面积＝=-=.
∴＝－（）＝.
（2）连接AD
∵在中，AB=AC
∴∠ABC=∠ACB=∠ADB
∵四边形ABCD是的内接四边形
∴∠ADF=∠ABC=∠ADE.
∵BD是△ABC的角平分线
∴∠ABD=∠ACD=∠CAD
∵AF是的切线，则∠FAD是的弦切角
∴由弦切角定理，得∠FAD=∠FCA=∠DAE
在△ADE和△ADF中，
∴△ADF≌△ADE(ASA)
∴DF=DE=4
∵,∴DC=6.
∵∠DCE=∠DBC,∠CDE=∠CDB
∴△DCE∽△DBC
∴,即,∴DB=9
∴BE=DB-DE=9-4=5.
5.如图，为的直径，为延长线上一点，是的切线，为切点，于点，交于点．

（1）求证：；
（2）若，，求的长．
【答案】（1）详见解析；（2）2
【解析】
【分析】
（1）连接OD，根据圆周角定理得到∠ADB＝90°，根据平行线的性质得到∠AOF＝∠B，根据切线的性质得到∠CDO＝90°，等量代换即可得到结论；
（2）根据三角形中位线定理得到OE＝BD＝×8＝4，设OD＝x，OC＝3x，根据相似三角形的性质即可得到结论．
【详解】
解：（1）连接OD，

∵AB为⊙O的直径，
∴∠ADB＝90°，
∴AD⊥BD，
∵OF⊥AD，
∴OF∥BD，
∴∠AOF＝∠B，
∵CD是⊙O的切线，D为切点，
∴∠CDO＝90°，
∴∠CDA＋∠ADO＝∠ADO＋∠BDO＝90°，
∴∠CDA＝∠BDO，
∵OD＝OB，
∴∠ODB＝∠B，
∴∠AOF＝∠ADC；
（2）∵OF∥BD，AO＝OB，
∴AE＝DE，
∴OE＝BD＝×8＝4，
∵sinC＝＝，
∴设OD＝x，OC＝3x，
∴OB＝x，
∴CB＝4x，
∵OF∥BD，
∴△COF∽△CBD，
∴，
∴，
∴OF＝6，
∴EF＝OF−OE＝6−4＝2．
【点睛】
本题考查了切线的性质，相似三角形的判定和性质，三角形的中位线定理，平行线的判定和性质，正确的作出辅助线是解题的关键．
6.如图，与相切于点，交于点，的延长线交于点，是上不与重合的点，．

（1）求的大小；
（2）若的半径为3，点在的延长线上，且，求证：与相切．
【答案】（1）60°；（2）详见解析
【解析】
【分析】
(1)连接OB，在Rt△AOB中由求出∠A=30°，进而求出∠AOB=60°，∠BOD=120°，再由同弧所对的圆周角等于圆心角的一半可以求出∠BED的值；
(2)连接OF，在Rt△OBF中，由可以求出∠BOF=60°，进而得到∠FOD=60°，再证明△FOB≌△FOD，得到∠ODF=∠OBF=90°．
【详解】
解：(1)连接，

∵与相切于点，
∴，
∵，∴，
∴，则．
由同弧所对的圆周角等于圆心角的一半可知：
．
故答案为：．
(2)连接，

由(1)得，，
∵，，∴，
∴，∴．
在与中，
∴，
∴．
又点在上，故与相切．
【点睛】
本题考查圆的有关性质、直线与圆的位置关系、特殊角的三角函数值、解直角三角形、全等三角形的判定和性质，熟练掌握其性质是解决此类题的关键．
7.如图，是⊙的直径，点在的延长线上， 、是⊙上的两点，，，延长交的延长线于点
（1）求证：是⊙的切线；
（2）求证：
（3）若,,求弦的长.

【分析】（1）连接OC，可证得∠CAD＝∠BCD，由∠CAD+∠ABC＝90°，可得出∠OCD＝90°，即结论得证；（2）证明△ABC≌△AFC可得CB＝CF，又CB＝CE，则CE＝CF；（3）证明△CBD∽△DCA，可求出DA的长，求出AB长，设BC＝a，AC＝a，则由勾股定理可得AC的长．
【解析】（1）连接OC，

∵AB是⊙O的直径，∴∠ACB＝90°，∴∠CAD+∠ABC＝90°，∵CE＝CB，∴∠CAE＝∠CAB，∵∠BCD＝∠CAE，∴∠CAB＝∠BCD，∵OB＝OC，∴∠OBC＝∠OCB，∴∠OCB+∠BCD＝90°，∴∠OCD＝90°，
∴CD是⊙O的切线；
（2）∵∠BAC＝∠CAE，∠ACB＝∠ACF＝90°，AC＝AC，∴△ABC≌△AFC（ASA），∴CB＝CF，
又∵CB＝CE，∴CE＝CF；
（3）∵∠BCD＝∠CAD，∠ADC＝∠CDB，∴△CBD∽△DCA，∴，∴，∴DA＝2，
∴AB＝AD﹣BD＝2﹣1＝1，设BC＝a，AC＝a，由勾股定理可得：，解得：a＝，
∴．
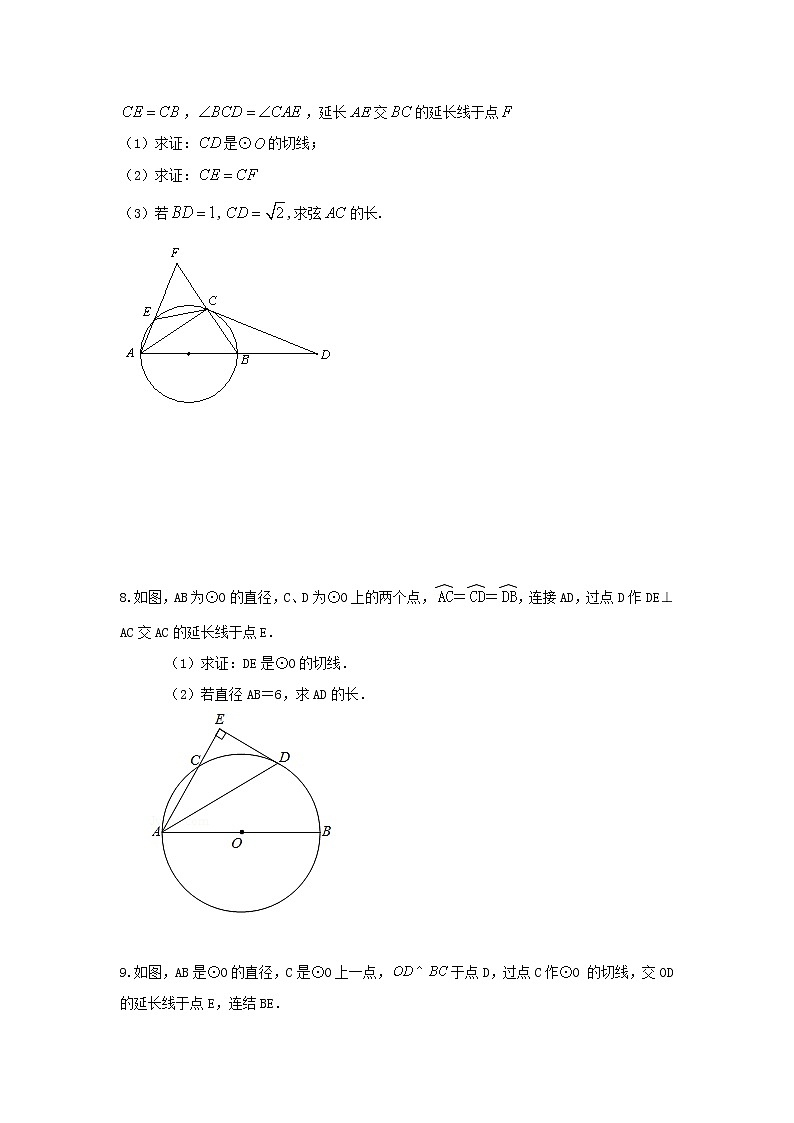
8.如图，AB为⊙O的直径，C、D为⊙O上的两个点，＝＝，连接AD，过点D作DE⊥AC交AC的延长线于点E．
（1）求证：DE是⊙O的切线．
（2）若直径AB＝6，求AD的长．

【分析】（1）连接OD，根据已知条件得到∠BOD＝180°＝60°，根据等腰三角形的性质得到∠ADO＝∠DAB＝30°，得到∠EDA＝60°，求得OD⊥DE，于是得到结论；
（2）连接BD，根据圆周角定理得到∠ADB＝90°，解直角三角形即可得到结论．
【解答】（1）证明：连接OD，
∵＝＝，
∴∠BOD＝180°＝60°，
∵＝，
∴∠EAD＝∠DAB＝BOD＝30°，
∵OA＝OD，
∴∠ADO＝∠DAB＝30°，
∵DE⊥AC，
∴∠E＝90°，
∴∠EAD+∠EDA＝90°，
∴∠EDA＝60°，
∴∠EDO＝∠EDA+∠ADO＝90°，
∴OD⊥DE，
∴DE是⊙O的切线；
（2）解：连接BD，
∵AB为⊙O的直径，
∴∠ADB＝90°，
∵∠DAB＝30°，AB＝6，
∴BD＝AB＝3，
∴AD＝＝3．

【点评】本题考查了切线的判定和性质，勾股定理，圆周角定理，正确的作出辅助线是解题的关键．
9.如图，AB是⊙O的直径，C是⊙O上一点，于点D，过点C作⊙O 的切线，交OD的延长线于点E，连结BE．
（1）求证：BE是⊙O的切线；
（2）设OE交⊙O于点F，若，求线段EF的长；
（3）在（2）的条件下，求阴影部分的面积．

{答案}（1）证明：连接OC，如图，∵OD⊥BC，∴CD=BD，∴OE为BC的垂直平分线，
∴EB=EC，∴∠EBC=∠ECB，∵OB=OC，∴∠OBC=∠OCB，
∴∠OBC+∠EBC=∠OCB+∠ECB，即∠OBE=∠OCE，∵CE为⊙O的切线，∴OC⊥CE，∴∠OCE=90°，
∴∠OBE=90°，∴OB⊥BE，∴BE与⊙O相切．
（2）设⊙O的半径为R，则OD=R-DF=R-2，OB=R，在Rt△OBD中，BD=BC=
∵OD2+BD2=OB2，∴，解得R=4，∴OD=2，OB=4，
∴∠OBD=30°，∴∠BOD=60°，∴在Rt△OBE中，∠BEO=30º，OE=2OB=8，
∴EF=OE-OF=8-4=4，即EF=4；
（3）由∠OCD=∠OBD=30º和OD⊥BC知：∠COD=∠BOD=60º，
∴∠BOC=120º，又BC=，OE=8，∴=
,


【解析】本题考查了切线的判定与性质、垂径定理、扇形面积的计算、含30º角的直角三角形边角关系、勾股定理等知识，熟练掌握每个知识点是解答的关键．
（1）连接OC，如图，根据垂径定理由OD⊥BC得到CD=BD，则OE为BC的垂直平分线，所以EB=EC，根据等腰三角形的性质得∠EBC=∠ECB，加上∠OBC=∠OCB，则∠OBE=∠OCE；再根据切线的性质得∠OCE=90°，所以∠OBE=90°，然后根据切线的判定定理得BE与⊙O相切；
（2）设⊙O的半径为R，则OD=R-DF=R-2，OB=R，在Rt△OBD，利用勾股定理解得R=4，再利用含30º角的直角三角形边角关系可求得OE，利用EF=OE-OF即可解答；
（3）利用（2）中可求得∠BOC=120º,然后利用代入数值即可求解．
10.如图，△ABC内接于⊙O，BD为⊙O的直径，BD与AC相交于点H，AC的延长线与过点B的直线相交于点E，且∠A＝∠EBC.
(1)求证：BE是⊙O的切线；
(2)已知CG∥EB，且CG与BD，BA分别相交于点F，G，若BG·BA＝48，FG＝，DF＝2BF，求AH的值．

【分析】：(1)证∠EBD＝90°即可；(2)由△ABC∽△CBG得＝，可求出BC，再由△BFC∽△BCD得BC2＝BF·BD，可求出BF，再求出CF，CG，GB，通过计算发现CG＝AG，可证CH＝CB，即可求出AC.
【答案】：(1)连接CD，∵BD是直径，∴∠BCD＝90°，即∠D＋∠CBD＝90°，∵∠A＝∠D，∠A＝∠EBC，∴∠CBD＋∠EBC＝90°，∴BE⊥BD，∴BE是⊙O切线
(2)∵CG∥EB，∴∠BCG＝∠EBC，∴∠A＝∠BCG，又∵∠CBG＝∠ABC，∴△ABC∽△CBG，∴＝，即BC2＝BG·BA＝48，∴BC＝4，∵CG∥EB，∴CF⊥BD，∴△BFC∽△BCD，∴BC2＝BF·BD，∵DF＝2BF，∴BF＝4，在Rt△BCF中，CF＝＝4，∴CG＝CF＋FG＝5，在Rt△BFG中，BG＝＝3，∵BG·BA＝48，∴BA＝8，∴AG＝5，∴CG＝AG，∴∠A＝∠ACG＝∠BCG，∠CFH＝∠CFB＝90°，∴∠CHF＝∠CBF，∴CH＝CB＝4，∵△ABC∽△CBG，∴＝，∴AC＝＝，∴AH＝AC－CH＝
11.如图，四边形ABCD内接于⊙O，对角线AC为⊙O的直径，过点C作AC的垂线交AD的延长线于点E，点F为CE的中点，连接DB，DC，DF.
(1)求∠CDE的度数；
(2)求证：DF是⊙O的切线；
(3)若AC＝2DE，求tan∠ABD的值．

【答案】：(1)∵对角线AC为⊙O的直径，∴∠ADC＝90°，∴∠EDC＝90°
(2)连接DO，∵∠EDC＝90°，F是EC的中点，∴DF＝FC，∴∠FDC＝∠FCD，∵OD＝OC，∴∠OCD＝∠ODC，∵∠OCF＝90°，∴∠ODF＝∠ODC＋∠FDC＝∠OCD＋∠DCF＝∠OCF＝90°，∴DF是⊙O的切线
(3)∵∠E＋∠DCE＝90°，∠DCA＋∠DCE＝90°，∴∠DCA＝∠E，又∵∠ADC＝∠CDE＝90°，∴△CDE∽△ADC，∴＝，∴DC2＝AD·DE.设DE＝x，则AC＝2x，AC2－AD2＝DC2＝AD·DE，即(2x)2－AD2＝AD·x，整理得AD2＋AD·x－20x2＝0，解得AD＝4x或AD＝－5x(舍去)，则DC＝＝2x，故tan∠ABD＝tan∠ACD＝＝＝2
12.已知的半径为，的半径为.以为圆心，以的长为半径画弧，再以线段的中点为圆心，以的长为半径画弧，两弧交于点，连接，，交于点，过点作的平行线交于点.

（1）求证：是的切线；
（2）若，，，求阴影部分的面积.
【解析】（1）证切线常用的方法有“作垂线证半径”和“作半径证垂直” ，考虑到题目中的已知条件，用“作垂线证半径”更简便一些，为此我们可以过点作直线BC的垂线，垂足为点M；同时考虑到∠O1A O2可能是直角，可以连接AP用等腰三角形的等角对等边和三角形内角和定理进行证明；条件中还给出了平行线，因此可以证明∠ABC＝90°，则四边形ABM O2是平行四边形，最后证明O2M＝AB= O1A－O1B= ，问题得以解决.
（2）求阴影部分的面积，可以根据割补法来求.解决问题的关键是分别求出△BO1C和扇形BO1N的面积，根据已知条件，可以先求出O1A =，然后根据三角函数求出
∠A O1 O2的度数，需要的数据再通过三角函数求出，问题得解.
{答案}证明：（1）连接AP，过点作直线BC的垂线，垂足为点M，如下图：
∵线段的中点是点，以的长为半径画弧∴
∴∠PAO1＝∠PO1A，∠PAO2＝∠PO2A，∴∠O1A O2=∠PAO1+∠PAO2＝90°
∴△O1A O2是直角三角形∵∴∠O1A O2=∠ABC＝90°
又∵∠O2MB=90°∴四边形ABM O2是平行四边形∴O2M＝AB= O1A－O1B=
∴是的切线；

（2）
∵，，， ∴O1A =
又∵∠O1A O2=90°∴cos∠A O1 O2=∴∠A O1 O2=60°
在Rt△B O1 C中：
设O1 O2与的交点为点N，则阴影部分的面积为：
.

13.如图，AB是⊙O的直径，C是⊙O上一点，过点O作OD⊥AB，交BC的延长线于D，交AC于点E，F是DE的中点，连接CF．
（1）求证：CF是⊙O的切线．
（2）若∠A＝22.5°，求证：AC＝DC．

【分析】（1）根据圆周角定理得到∠ACB＝∠ACD＝90°，根据直角三角形的性质得到CF＝EF＝DF，求得∠AEO＝∠FEC＝∠FCE，根据等腰三角形的性质得到∠OCA＝∠OAC，于是得到结论；
（2）根据三角形的内角和得到∠OAE＝∠CDE＝22.5°，根据等腰三角形的性质得到∠CAD＝∠ADC＝45°，于是得到结论．
【解析】证明：（1）∵AB是⊙O的直径，
∴∠ACB＝∠ACD＝90°，
∵点F是ED的中点，
∴CF＝EF＝DF，
∴∠AEO＝∠FEC＝∠FCE，
∵OA＝OC，
∴∠OCA＝∠OAC，
∵OD⊥AB，
∴∠OAC+∠AEO＝90°，
∴∠OCA+∠FCE＝90°，即OC⊥FC，
∴CF与⊙O相切；
（2）解：∵OD⊥AB，AC⊥BD，
∴∠AOE＝∠ACD＝90°，
∵∠AEO＝∠DEC，
∴∠OAE＝∠CDE＝22.5°，
∵AO＝BO，
∴AD＝BD，
∴∠ADO＝∠BDO＝22.5°，
∴∠ADB＝45°，
∴∠CAD＝∠ADC＝45°，
∴AC＝CD．

14.如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，且BD＝BC，延长AD到E，且有∠EBD＝∠CAB.
(1)求证：BE是⊙O的切线；
(2)若BC＝，AC＝5，求圆的直径AD及切线BE的长．

【答案】：(1)连接OB，∵BD＝BC，∴∠CAB＝∠BAD，∵∠EBD＝∠CAB，∴∠BAD＝∠EBD，∵AD是⊙O的直径，∴∠ABD＝90°，OA＝OB，∴∠BAD＝∠ABO，∴∠EBD＝∠ABO，∴∠OBE＝∠EBD＋∠OBD＝∠ABO＋∠OBD＝∠ABD＝90°，∵点B在⊙O上，∴BE是⊙O的切线
(2)设圆的半径为R，连接CD，∵AD为⊙O的直径，∴∠ACD＝90°，∵BC＝BD，∴OB⊥CD，∴OB∥AC，∵OA＝OD，∴OF＝AC＝，∵四边形ACBD是圆内接四边形，∴∠BDE＝∠ACB，∵∠DBE＝∠CAB，∴△DBE∽△CAB，∴＝，∴＝，∴DE＝，∵∠OBE＝∠OFD＝90°，∴DF∥BE，∴＝，∴＝，∵R＞0，∴R＝3，∴AB＝＝，∵＝，∴BE＝
15.如图点P为正方形ABCD的对角线AC上的一点，连接BP并延长交CD于点E，交AD的延长线于点F，⊙O是△DEF的外接圆，连接DP.
（1）求证：DP是⊙O的切线；
（2）若tan∠PDC=，正方形ABCD的边长为4，求⊙O的半径和线段OP的长.

解：（1）连接OD，

∵正方形ABCD中，CD=BC，CP=CP，∠DCP=∠BCP=45°，
∴△CDP≌△CBP（SAS），∴∠CDP=∠CBP.
∵∠BCD=90°，∴∠CBP+∠BEC=90°.
∵OD=OE，∴∠ODE=∠OED，∠OED=∠BEC，
∴∠BEC=∠OED=∠ODE，∴∠CDP+∠ODE=90°，∴∠ODP=90°，∴DP是⊙O的切线.
（2）∵∠CDP=∠CBE，∴tan∠CBE＝tan∠CDP＝＝，∴CE=×4＝2，∴DE=2.
∵∠EDF=90°，∴EF是⊙O的直径，∴∠F+∠DEF=90°，∴∠F=∠CDP.
在Rt△DEF中，=，∴DF=4，∴EF＝==2，∴OE＝.
∵∠F=∠PDE，∠DPE=∠FPD，
∴△DPE∽△FPD，∴，
设PE=x，则PD=2x，∴x(x+2)＝(2x)2，解得x=
，∴OP=OE+EP=+=．
16.如图，已知 AB 是⊙O 的直径，CD 与⊙O 相切于点 D，且 AD//OC．
（1）求证：BC 是⊙O 的切线；
（2）延长 CO 交⊙O 于点 E．若∠CEB＝30°，⊙O 的半径为 2，求 的长．（结果保留 π ）
答案：解：（1）证明：连接OD，如答图所示．


∵AD//OC，
∴∠COD＝∠ADO，∠COB＝∠DAO，
又∵OA＝OD，∴∠ADO＝∠DAO，
∴∠COD＝∠COB，
在△COD和△COB中，
∴△COD≌COB，
∴∠CDO＝∠CBO，
又CD 与⊙O 相切于点 D，
∴∠CDO＝90°，
∴∠CBO＝90°，
∴BC 是⊙O 的切线；
（2）∵∠CEB＝30°，∴∠COB＝60°，
由（1）知，∠COD＝∠COB，
∴∠COD＝60°，
∴∠DOB＝∠COD＋∠COB＝120°
∵⊙O 的半径为 2，
∴的长＝＝．