2022届优质校一模试卷专题汇编3 函数 解析版

这是一份2022届优质校一模试卷专题汇编3 函数 解析版，共22页。试卷主要包含了选择题．，填空题．等内容，欢迎下载使用。
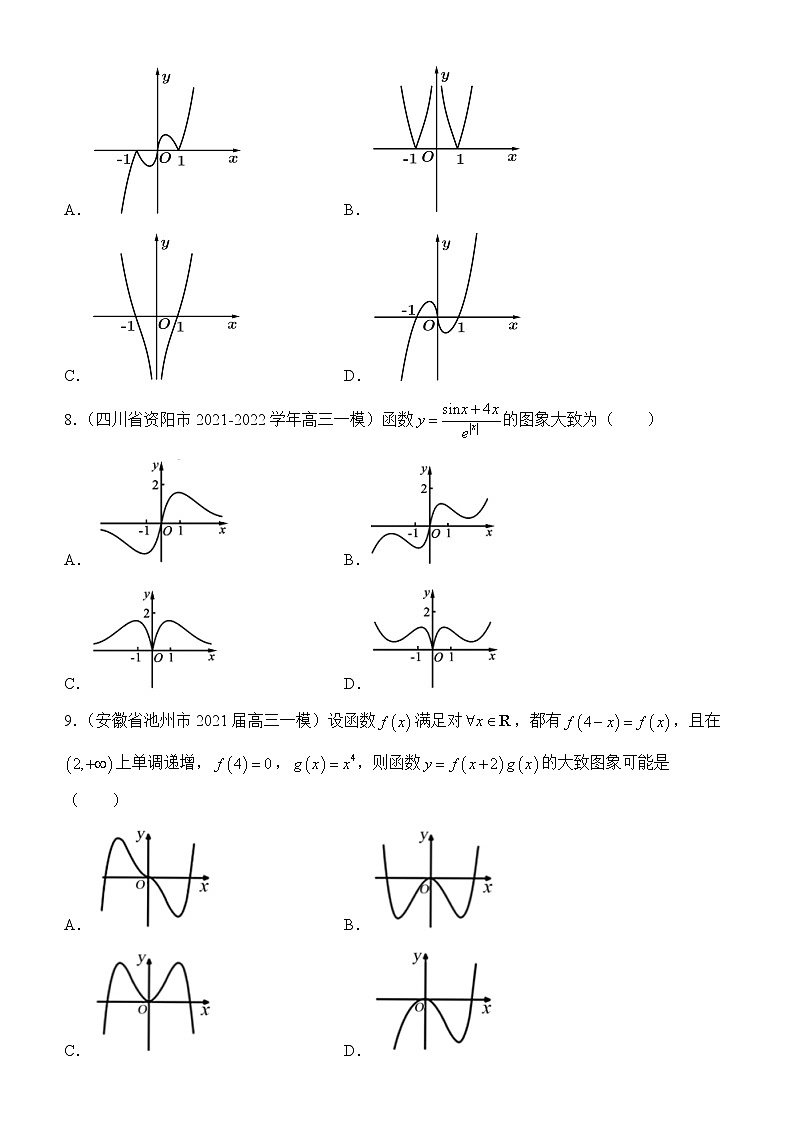
    函数是高考的必考内容，考查的题型主要有函数性质、函数图象、零点问题、指数幂的大小比较，与生活实际相关或函数文化结合的题．（1）函数性质的考查主要为奇偶性、单调性、对称性、周期性的综合考查，要求学生熟悉一些相关结论的由来与应用，例如由得到关于对称．（2）对于函数图象的题型，我们一般优先考虑函数的奇偶性，或结合函数的平移、伸缩变换考虑函数的对称性，然后再考虑自变量取某些特殊值时，对应的函数值的一些特点，比如函数值的正负，最后考虑函数的单调性．（3）函数的零点问题一般可以转化成函数方程的根、函数图象与轴的交点个数、函数图象与某条水平线的交点个数问题、函数图象与某条斜直线的交点问题，或两条曲线的交点个数问题等．（4）与生活实际相关或函数文化结合的题一般相对简单，要求学生耐心理解题目意思，知道题中每个量，每个公式所具有的意义． 一、选择题．1．（江西省南昌市2021届高三一模）如图所示某加油站地下圆柱体储油罐示意图，已知储油罐长度为，截面半径为（为常量），油面高度为，油面宽度为，储油量为（为变量），则下列说法：①是的函数   ②是的函数   ③是的函数   ④是的函数其中正确的个数是（    ）A．1个 B．2个 C．3个 D．4个2．（河南省联考2021-2022学年高三一模）已知函数，则（    ）A． B． C． D．3．（贵州省遵义市2021届高三一模）已知函数，则（    ）A． B． C． D．4．（福建省龙岩市2021届高三一模）定义在R上的奇函数满足，当时，（e为自然对数的底数），则的值为（    ）A． B． C． D．05．（四川省资阳市2020-2021学年高三一模）定义在上的偶函数满足，则（    ）A．或4 B．或3 C．3 D．46．（广东省佛山市顺德区2022届高三一模数学试题）已知函数，则函数的大致图象为（    ）A． B．C． D．7．（四川省南充市2021-2022学年高三一模）函数的图象大致是（    ）A． B．C． D．8．（四川省资阳市2021-2022学年高三一模）函数的图象大致为（    ）A． B．C． D．9．（安徽省池州市2021届高三一模）设函数满足对，都有，且在上单调递增，，，则函数的大致图象可能是（    ）A． B．C． D．10．（江苏省连云港市灌云县第一中学2021-2022学年高三一模）我国著名数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休．”在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来研究函数图象的特征．我们从这个商标中抽象出一个图象如图，其对应的函数可能是（    ）A． B． C． D．11．（四川省南充市2021-2022学年高三一模）农业农村部于年月日发布信息：全国按照主动预防、内外结合、分类施策、有效处置的总体要求，全面排查蝗灾隐患．为了做好蝗虫防控工作，完善应急预案演练，专家假设蝗虫的日增长率为，最初有只，则大约经过（    ）天能达到最初的倍．（参考数据：，，，．）A． B． C． D．12．（广西柳州市2022届高三11月第一次模拟）5G技术的数学原理之一是著名的香农公式：它表示：在受高斯白噪声干扰的信道中，最大信息传递速率C取决于信道带宽W﹒信道内所传信号的平均功率S，信道内部的高斯噪声功率N的大小．其中叫做信噪比，按照香农公式，在不改变W的情况下，将信噪比卡从1999提升至，使得C大约增加了20%，则入的值约为（    ）(参考数据，)A．9121 B．9119 C．9919 D．1099913．（四川省达州市2021-2022学年高三一模）天文学中，用视星等表示观测者用肉眼所看到的星体亮度，用绝对星等反映星体的真实亮度．星体的视星等，绝对星等，距地球的距离有关系式（为常数）．若甲星体视星等为，绝对星等为，距地球距离；乙星体视星等为，绝对星等为，距地球距离，则（    ）A． B． C． D．14．（江苏省苏州市八校2020-2021学年高三一模）若函数满足：对定义域内任意的，有，则称函数具有性质．则下列函数中不具有性质的是（    ）A．  B．C． D．15．（四川省资阳市高中2021-2022学年高三一模）设，，，则a，b，c大小关系为（    ）A． B． C． D．16．（2020山东一模）已知定义在上的函数，，，，则，，的大小关系为（    ）A． B． C． D．17．（湖北省武汉市部分学校2020届高三一模）已知，，，则，，的大小关系是（    ）A． B． C． D．18．（天津市河北区2020-2021学年高三一模）设，，，则a，b，c的大小关系为（    ）A． B． C． D．19．（江西省赣州市2021届高三一模）设函数（且）．若，，则（    ）A．1 B．2 C．3 D．420．（江苏省2021年对口高考单招一模）若函数，（a，）为奇函数，则的值为（    ）A． B． C．1 D．421．（四川省资阳市2021-2022学年高三一模）已知函数，则满足不等式的实数的取值范围是（    ）A． B． C． D．22．（多选）（广东省普宁市勤建学校2021届高三一模）定义在上的函数满足，且在上是增函数，给出下列真命题的有（    ）A．是周期函数 B．的图象关于直线对称C．在上是减函数 D．23．（辽宁省鞍山市第一中学2018届高三上一模）指数函数（，且）在上是减函数，则函数在其定义域上的单调性为（    ）A．单调递增  B．单调递减C．在上递增，在上递减 D．在上递减，在上递增24．（山东省烟台市2021届高三一模）已知是定义在上的奇函数，，当时，，则（    ）A．  B．是的一个周期C．当时， D．的解集为25．（山东省青岛胶州市2019-2020一模）已知函数的定义域为，且是偶函数，是奇函数，在上单调递增，则（    ）A． B．C． D．26．（吉林省长春市2022届高三一模）设函数的定义域为，且是偶函数，是奇函数，则下列说法一定正确的有（    ）①；②；③；④．A．4个 B．3个 C．2个 D．1个27．（四川省南充市2021-2022学年高三一模）设函数的定义域为，为奇函数，为偶函数，当时，，若，则（    ）A． B． C． D．28．（陕西省渭南市临渭区2021届高三一模）函数的零点有（    ）A．0个 B．1个 C．2个 D．3个29．（多选）（2021届高三下学期一模）若直线与函数（，且）的图象有两个公共点，则的取值可以是（    ）A． B． C． D．230．（四川省成都市2020-2021学年高三一模）若函数有且仅有一个零点，则实数的取值范围为（    ）A． B．C．  D．31．（安徽省合肥市2020-2021学年高三一模）设函数．若时，方程有唯一解，则实数的取值范围为（    ）A． B． C． D．32．（四川省成都市新都区2021-2022学年高三一模）已知函数，函数满足以下三点条件：①定义域为；②对任意，有；③当时，．则函数在区间上的零点个数为（    ）A． B． C． D．33．（2020届浙江省金华十校高三一模）已知函数，下列关于函数的零点个数的判断，正确的是（    ）A．当，m∈R时，有且只有1个 B．当，时，都有3个C．当，时，都有4个 D．当，时，都有4个34．（山东省实验中学2021届高三一模）已知是定义在R上的奇函数，当时，，则关于的函数的所有零点之和为（    ）A． B． C． D．35．（安徽省滁州市定远中学2019-2020学年一模）已知函数，函数有四个不同的零点，从小到大依次为，，，，则的取值范围为（    ）A． B． C． D． 二、填空题．36．（江苏省2021年对口高考单招一模数学）在平面直角坐标系中，函数（且）的图象恒过定点P，若角θ的终边过点P，则________．  
 一、选择题．1．【答案】B【解析】因为，所以，所以是的函数，故④正确；因为，所以，对于的每一个取值，都有2个与之对应，所以不是的函数，故③不正确；由知，对于的每一个取值，都有2个与之对应，而对于的每一个取值，弓形的面积都有一个取值与之对应，所以根据柱体体积公式可知，对于的每一个取值，都有2个与之对应，所以不是的函数，故②不正确；根据柱体体积公式可知，对于每一个确定的，都有唯一的一个与之对应，对于每一个确定的，都有唯一的与之对应，所以是的函数，故①正确，故选B．2．【答案】D【解析】因为，所以，故选D．3．【答案】D【解析】，故选D．4．【答案】A【解析】定义在上的奇函数满足，当时，，，且，可得且，故，故选A．5．【答案】D【解析】由，得，则的图象关于直线对称，于是，故的一个周期为4，由，令，得，，解得或（负值舍去），所以，故选D．6．【答案】B【解析】由题可知：函数定义域为，，所以，故该函数为奇函数，排除A、C；又，所以排除D，故选B．7．【答案】C【解析】由得，即函数的定义域为，又，所以是偶函数，其图象关于轴对称，故A、D错；又时，，，所以，故B错，C正确，故选C．8．【答案】A【解析】由题意，函数的定义域为，且，所以函数为奇函数，图象关于原点对称，排除C、D；当时，可得，且时，，结合选项，可得A选项符合题意，故选A．9．【答案】B【解析】依题意可知函数的对称轴方程为，在上单调递增，且，设，则函数的对称轴方程为，在上单调递增，且，所以是偶函数，且当时，．因此函数也是偶函数，其图象关于轴对称，故可以排除选项A和D；当时，，由此排除选项C，故选B．10．【答案】B【解析】由图知的定义域为，排除选项A、D；又因为当时，，不符合图象，所以排除选项C，故选B．11．【答案】A【解析】由题意可知，蝗虫最初有只且日增长率为，设经过天后蝗虫数量达到原来的倍，则，，，，大约经过天能达到最初的倍，故选A．12．【答案】B【解析】由题意得：，，，又，故，，故选B．13．【答案】A【解析】由已知可得，上述两个等式作差得，因此，，故选A．14．【答案】B【解析】A．，符合要求；B．，不符合要求；C．，符合要求；D．，符合要求，故选B．15．【答案】D【解析】由，即，又，可得，即，∴，故选D．16．【答案】D【解析】由题意，定义在上的函数的定义域为，关于原点对称，且，所以函数为奇函数，所以，又由当时，结合初等函数的性质，可得函数为单调递增函数，又由对数的运算性质可得，所以，即，故选D．17．【答案】B【解析】对于的大小：，，明显；对于的大小：构造函数，则，当时，在上单调递增；当时，在上单调递减，，，即，，，对于的大小：，，，，故选B．18．【答案】D【解析】，，又，∴，故选D．19．【答案】B【解析】设，则，因为的定义域为R，，所以为奇函数，所以，所以，故选B．20．【答案】B【解析】利用和可得，解得，，所以，，故选B．21．【答案】B【解析】因为的定义域为，，所以是奇函数，又当时，，恒成立，所以在上递增，所以在上单调递增，因为，所以，解得，故选B．22．【答案】ACD【解析】令，得，所以，令，则，即，所以是奇函数，，所以是周期函数，4是它的一个周期，A正确；，函数图象关于点对称，B错；，函数图象关于直线对称，又在上递增，因此在上递增，所以在上是减函数，C正确；，D正确，故选ACD．23．【答案】C【解析】结合指数函数的性质可知：，函数的导函数：，当时，，函数单调递减；当时，，函数单调递增，本题选择C选项．24．【答案】D【解析】因为是定义在上的奇函数，所以，所以，所以，所以的最小正周期是4，故B错误；，故A错误；因为当时，，是定义在上的奇函数，所以当时，，当时，，，故C错误；因为当时，，的最小正周期是4，所以的解集为，故D正确，故选D．25．【答案】B【解析】是偶函数，得，即，是奇函数，得，即，，得，由是奇函数，得，因为在上单调递增，所以，，，所以，故选B．26．【答案】B【解析】由题意，函数是奇函数，可得的图象关于点对称，所以，所以②正确；令，则，又由是偶函数，所以的图象关于对称，所以的图象关于对称，则有，令，则，所以③正确；在中，将用替换，则，在中，将用替换，则，所以，再将用替换，则，所以，所以①正确；对于④中，由，无法推出其一定相等，故选B．27．【答案】C【解析】因为为奇函数，所以①；又为偶函数，所以②；令，由②得：，又，所以，得，令，由①得；令，由②得，所以，得时，，结合①②得，，所以函数的周期为，所以，故选C．28．【答案】B【解析】由题意知函数的定义域为，由，得，所以，所以函数的零点有1个，故选B．29．【答案】AB【解析】（1）当时，由题得，，因为，所以此种情况不存在；（2）当时，由题得，，因为，所以，故选AB．30．【答案】A【解析】由题意知：，∴时，，得或；时，，得，∴在上递增，上递减，上递增，当时，有极大值；当时，有极小值，∴只有当或时，函数有且仅有一个零点，∴或，故选A．31．【答案】B【解析】因为函数，所以，若时，作出的图象，结合图象可知方程有唯一解，则，故选B．32．【答案】A【解析】因为函数的定义域为，所以在无零点；∵，故将的图象向右平移个单位后，图象纵向伸长为原来的两倍，∴在平面直角坐标系，的图象以及在上如图所示：又，故、在上的图象共有5个不同交点，故选A．33．【答案】B【解析】令，则，当时，若，则或，即或，即当，时，不是有且只有1个零点，故A错误；当时，时，可得或，可得的个数为个，即B正确；当，或时，由，且，可得零点的个数为1个或3个，故C，D错误，故选B．34．【答案】C【解析】∵时，，即时，；时，；时，，画出时，的图象，再利用奇函数的对称性，画出时，的图象，如图所示：直线与共有5个交点，则方程共有五个实根，最左边两根之和为，最右边两根之和为6，∵时，，∴，又，∴，∴中间的一个根满足，即，得，∴所有根的和为，故选C．35．【答案】D【解析】当时，，；，则函数在上单调递减，在上单调递增，且，当时，，；，则函数在上单调递减，在上单调递增，，函数有四个不同的零点，即两函数与图象有四个不同的交点，如下图所示：由图可知，，是方程的两根，即的两根，所以，是方程的两根，即的两根，所以，，故选D． 二、填空题．36．【答案】【解析】由题意，函数，令，可得，此时，即函数恒过定点，则，根据三角函数的定义，可得，，所以，故答案为．